
Ačkoli, jak je uvedeno v kapitole Analýza toku signálu, je určitá forma analýzy toku signálu nejobecnějším způsobem, jak zpracovat zesilovač se zápornou zpětnou vazbou, zobrazení jako dva dvouporty je přístup, který je nejčastěji uváděn v učebnicích a který je zde prezentován. Zachovává dvoublokové rozdělení obvodu zesilovače, ale umožňuje, aby bloky byly oboustranné. Některé nevýhody této metody jsou popsány na konci.
Elektronické zesilovače používají jako vstup a výstup proud nebo napětí, takže jsou možné čtyři typy zesilovačů (libovolný ze dvou možných vstupů s libovolným ze dvou možných výstupů). Viz klasifikace zesilovačů. Cílem pro zpětnovazební zesilovač může být kterýkoli z těchto čtyř typů zesilovačů a nemusí být nutně stejný typ jako zesilovač s otevřenou smyčkou, který sám může být kterýkoli z těchto typů. Tak lze například uspořádat optický zesilovač (napěťový zesilovač) tak, aby místo něj vznikl proudový zesilovač.
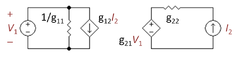
Záporné zesilovače se zpětnou vazbou libovolného typu lze realizovat pomocí kombinací dvouportových sítí. Existují čtyři typy dvouportových sítí a požadovaný typ zesilovače diktuje volbu dvouportů a výběr jedné ze čtyř různých topologií zapojení znázorněných na obrázku. Tato zapojení se obvykle označují jako sériová nebo boční (paralelní) zapojení. V levém sloupci diagramu jsou znázorněny boční vstupy, v pravém sloupci sériové vstupy. Horní řádek zobrazuje sériové výstupy; dolní řádek zobrazuje boční výstupy. Různé kombinace zapojení a dvouportů jsou uvedeny v následující tabulce.
| Typ zpětnovazebního zesilovače | Připojení vstupů | Připojení výstupů | Ideální zpětná vazba | Dva-portová zpětná vazba |
|---|---|---|---|---|
| Proudový | Bočník | Série | CCCS | g-parametr |
| Přechodový odpor | Bočník | Bočník | CCVS | y-parametr |
| Transvodivost | Série | Série | VCCS | z-parametr |
| Napětí | Série | Šunt | VCVS | h-parametr |
Např, u zesilovače s proudovou zpětnou vazbou je proud z výstupu vzorkován pro zpětnou vazbu a kombinován s proudem na vstupu. Proto se zpětná vazba v ideálním případě provádí pomocí (výstupního) proudově řízeného zdroje proudu (CCCS) a její nedokonalá realizace pomocí dvouportové sítě musí rovněž obsahovat CCCS, to znamená, že vhodnou volbou pro zpětnovazební síť je g-parametr dvouportový. Zde je uvedena dvouportová metoda používaná ve většině učebnic s využitím obvodu zpracovaného v článku o asymptotickém modelu zesílení.

Obrázek 3 ukazuje dvoutranzistorový zesilovač se zpětnovazebním rezistorem Rf. Cílem je analýzou tohoto obvodu zjistit tři položky: zesílení, výstupní impedanci při pohledu do zesilovače ze zátěže a vstupní impedanci při pohledu do zesilovače ze zdroje.
- Nahrazení zpětnovazební sítě dvouportovouUpravit
- Malosignálové zapojeníUpravit
- Zatížené zesílení v otevřené smyčceEdit
- Zisk se zpětnou vazbouEdit
- Vstupní a výstupní odporyEdit
- Základní informace o určování odporuUpravit
- Aplikace na příkladový zesilovačUpravit
- . Činitel zlepšení, který snižuje zesílení, a to ( 1 + βFB AOL), přímo rozhoduje o vlivu zpětné vazby na vstupní a výstupní odpory zesilovače. V případě bočníkového zapojení se o tento činitel sníží vstupní impedance a v případě sériového zapojení se impedance tímto činitelem násobí. Impedance, která je modifikována zpětnou vazbou, je však impedance zesilovače na obrázku 5 s vypnutou zpětnou vazbou a zahrnuje modifikace impedance způsobené rezistory zpětnovazební sítě.
- Zátěžové napětí a zátěžový proudUpravit
- Je hlavní blok zesilovače dvouportový? edit
Nahrazení zpětnovazební sítě dvouportovouUpravit
Prvním krokem je nahrazení zpětnovazební sítě dvouportovou. Jaké součástky do dvouportové sítě patří?
Na vstupní straně dvouportové sítě máme Rf. Pokud se změní napětí na pravé straně Rf, změní se proud v Rf, který se odečte od proudu vstupujícího do báze vstupního tranzistoru. To znamená, že vstupní strana dvouportového zesilovače je závislým zdrojem proudu řízeným napětím na vrcholu rezistoru R2.
Dalo by se říci, že druhý stupeň zesilovače je pouze napěťový sledovač, který přenáší napětí na kolektoru vstupního tranzistoru na vrchol R2. To znamená, že sledovaný výstupní signál je ve skutečnosti napětí na kolektoru vstupního tranzistoru. Tento pohled je oprávněný, ale pak se stupeň s napěťovým sledovačem stává součástí sítě zpětné vazby. To komplikuje analýzu zpětné vazby.
Alternativní pohled je, že napětí na vrcholu R2 je nastaveno emitorovým proudem výstupního tranzistoru. Tento pohled vede ke zcela pasivní síti zpětné vazby tvořené R2 a Rf. Veličinou řídící zpětnou vazbu je emitorový proud, takže zpětná vazba je proudově řízený zdroj proudu (CCCS). Projdeme čtyři dostupné dvouportové sítě a zjistíme, že jedinou sítí s CCCS je dvouportová síť s g-parametrem, která je znázorněna na obrázku 4. Dalším úkolem je zvolit g-parametry tak, aby dvouport na obrázku 4 byl elektricky ekvivalentní úseku L tvořenému R2 a Rf. Tato volba je algebraickým postupem, který se provádí nejjednodušeji tak, že se zkoumají dva jednotlivé případy: případ s V1 = 0, který činí VCVS na pravé straně dvojportu zkratem, a případ s I2 = 0, který činí CCCS na levé straně otevřeným obvodem. Algebra v těchto dvou případech je jednoduchá, mnohem jednodušší než řešení pro všechny proměnné najednou. Volba g-parametrů, díky nimž se dvouport a L-sekce chovají stejně, je uvedena v následující tabulce.
| g11 | g12 | g21 | g22 |
|---|---|---|---|
1 R f + R 2 {\displaystyle {\frac {1}{R_{\mathrm {f} }+R_{2}}}}
 |
– R 2 R 2 + R f {\displaystyle -{\frac {R_{2}}{R_{2}+R_{\mathrm {f} }}}}
 |
R 2 R 2 + R f {\displaystyle {\frac {R_{2}}{R_{2}+R_{\mathrm {f} }}}}
 |
R 2 / / R f {\displaystyle R_{2}//R_{\mathrm {f} }\ }
 |
Malosignálové zapojeníUpravit
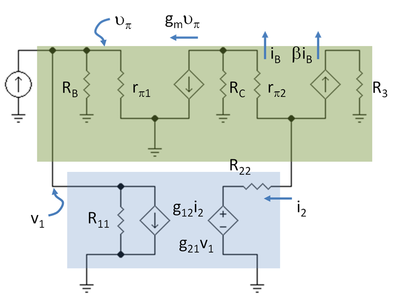
Dalším krokem je nakreslit malosignálové schéma zesilovače s dvouportem na místě s použitím modelu hybrid-pi pro tranzistory. Obrázek 5 ukazuje schéma se zápisem R3 = RC2 // RL a R11 = 1 / g11, R22 = g22.
Zatížené zesílení v otevřené smyčceEdit
Obrázek 3 naznačuje výstupní uzel, ale ne volbu výstupní veličiny. Užitečnou volbou je proudový výstup zesilovače nakrátko (což vede k zesílení proudu nakrátko). Protože tato proměnná vede jednoduše k některé z dalších voleb (například k zatěžovacímu napětí nebo zatěžovacímu proudu), je zesílení zkratového proudu nalezeno níže.
Nejprve je nalezeno zesílení zatížené otevřené smyčky. Zpětná vazba se vypne nastavením g12 = g21 = 0. Jde o to zjistit, jak moc se změní zesílení zesilovače kvůli samotným rezistorům ve zpětnovazební síti při vypnuté zpětné vazbě. Tento výpočet je celkem snadný, protože R11, RB a rπ1 jsou paralelně a v1 = vπ. Nechť R1 = R11 // RB // rπ1. Kromě toho i2 = -(β+1) iB. Výsledek pro proudové zesílení v otevřené smyčce AOL je:
A O L = β i B i S = g m R C ( β β + 1 ) ( R 1 R 22 + r π 2 + R C β + 1 ) . {\displaystyle A_{\mathrm {OL} }={\frac {\beta i_{\mathrm {B} }}{i_{\mathrm {S} }}}=g_{m}R_{\mathrm {C} }\levice({\frac {\beta }{\beta +1}}}pravá)\levice({\frac {R_{1}}{R_{22}+{\frac {r_{\pi 2}+R_{\mathrm {C}}) }}{\beta +1}}}}\right)\ .}

Zisk se zpětnou vazbouEdit
V klasickém přístupu ke zpětné vazbě se zanedbává zpětná vazba reprezentovaná VCVS (tj. g21 v1). Díky tomu se obvod na obrázku 5 podobá blokovému schématu na obrázku 1 a zesílení se zpětnou vazbou je pak:
A F B = A O L 1 + β F B A O L {\displaystyle A_{\mathrm {FB} }={\frac {A_{\mathrm {OL} }}{1+{\beta }_{\mathrm {FB} }A_{\mathrm {OL} }}}}

A F B = A O L 1 + R 2 R 2 + R f A O L , {\displaystyle A_{\mathrm {FB}}. }={\frac {A_{\mathrm {OL} }}{1+{\frac {R_{2}}{R_{2}+R_{\mathrm {f} }}}A_{\mathrm {OL} }}} ,}

kde faktor zpětné vazby βFB = -g12. Zápis βFB je zaveden pro činitel zpětné vazby, aby se odlišil od tranzistoru β.
Vstupní a výstupní odporyEdit

Zpětná vazba se používá pro lepší přizpůsobení zdrojů signálu jejich zátěži. Například přímé připojení zdroje napětí k odporové zátěži může vést ke ztrátě signálu v důsledku dělení napětí, ale vložením zesilovače se zápornou zpětnou vazbou lze zvýšit zdánlivou zátěž viditelnou zdrojem a snížit zdánlivou impedanci ovladače viditelnou zátěží, čímž se zabrání útlumu signálu dělením napětí. Tato výhoda se neomezuje pouze na napěťové zesilovače, ale analogické zlepšení přizpůsobení lze zařídit pro proudové zesilovače, transvodičové zesilovače a transodporové zesilovače.
K vysvětlení těchto účinků zpětné vazby na impedance je třeba nejprve udělat odbočku o tom, jak teorie dvou portů přistupuje k určování odporu, a poté její aplikaci na daný zesilovač.
Základní informace o určování odporuUpravit
Na obrázku 6 je znázorněn ekvivalentní obvod pro zjištění vstupního odporu zesilovače napětí se zpětnou vazbou (vlevo) a pro zesilovač proudu se zpětnou vazbou (vpravo). Tato uspořádání jsou typickými aplikacemi Millerovy věty.
V případě napěťového zesilovače je výstupní napětí βVout zpětnovazební sítě přivedeno sériově a s opačnou polaritou než vstupní napětí Vx procházející smyčkou (ale vzhledem k zemi jsou polarity stejné). V důsledku toho se efektivní napětí na vstupním odporu zesilovače Rin a proud jím procházející sníží, takže vstupní odpor obvodu se zvýší (dalo by se říci, že Rin zřejmě vzroste). Jeho novou hodnotu lze vypočítat pomocí Millerovy věty (pro napětí) nebo základních obvodových zákonů. Kirchhoffův napěťový zákon tedy stanoví:
V x = I x R i n + β v o u t , {\displaystyle V_{x}=I_{x}R_{\mathrm {in} }+\beta v_{\mathrm {out} }\ ,}

kde vout = Av vin = Av Ix Rin. Dosazením tohoto výsledku do výše uvedené rovnice a řešením pro vstupní odpor zpětnovazebního zesilovače dostaneme výsledek:
R i n ( f b ) = V x I x = ( 1 + β A v ) R i n . {\displaystyle R_{\mathrm {in} }(fb)={\frac {V_{x}}{I_{x}}=\left(1+\beta A_{v}\right)R_{\mathrm {in} }\ .}

Obecný závěr z tohoto příkladu a podobného příkladu pro případ výstupního odporu je:Sériové zapojení zpětné vazby na vstupu (výstupu) zvyšuje vstupní (výstupní) odpor o faktor ( 1 + β AOL ), kde AOL = zesílení otevřené smyčky.
Naopak pro proudový zesilovač platí, že výstupní proud βIout zpětnovazební sítě je aplikován paralelně a s opačným směrem než vstupní proud Ix. V důsledku toho se celkový proud protékající vstupem obvodu (nejen vstupním odporem Rin) zvětšuje a napětí na něm klesá, takže vstupní odpor obvodu se zmenšuje (Rin zřejmě klesá). Jeho novou hodnotu lze vypočítat použitím dvojí Millerovy věty (pro proudy) nebo základních Kirchhoffových zákonů:
I x = V i n R i n + β i o u t . {\displaystyle I_{x}={\frac {V_{\mathrm {in} }}{R_{\mathrm {in} }}}+\beta i_{\mathrm {out} }\ .}

kde iout = Ai iin = Ai Vx / Rin. Dosazením tohoto výsledku do výše uvedené rovnice a řešením pro vstupní odpor zpětnovazebního zesilovače dostaneme výsledek:
R i n ( f b ) = V x I x = R i n ( 1 + β A i ) . {\displaystyle R_{\mathrm {in} }(fb)={\frac {V_{x}}{I_{x}}={\frac {R_{\mathrm {in} }}{\left(1+\beta A_{i}\right)}}\ .}

Obecný závěr z tohoto příkladu a podobného příkladu pro případ výstupního odporu je:Paralelní zpětnovazební spojení na vstupu (výstupu) snižuje vstupní (výstupní) odpor o faktor ( 1 + β AOL ), kde AOL = zesílení otevřené smyčky.
Tyto závěry lze zobecnit pro případy s libovolnými Nortonovými nebo Théveninovými pohony, libovolnými zátěžemi a obecnými dvouportovými sítěmi zpětné vazby. Výsledky však závisí na tom, že hlavní zesilovač má reprezentaci jako dvouportový – to znamená, že výsledky závisí na tom, že do vstupních svorek vstupuje a z nich vystupuje stejný proud, a stejně tak stejný proud, který opouští jednu výstupní svorku, musí vstupovat do druhé výstupní svorky.
Širší závěr, nezávislý na kvantitativních detailech, je, že zpětnou vazbu lze použít ke zvýšení nebo snížení vstupní a výstupní impedance.
Aplikace na příkladový zesilovačUpravit
Tyto výsledky odporu nyní aplikujeme na zesilovač z obrázku 3 a obrázku 5.
. Činitel zlepšení, který snižuje zesílení, a to ( 1 + βFB AOL), přímo rozhoduje o vlivu zpětné vazby na vstupní a výstupní odpory zesilovače. V případě bočníkového zapojení se o tento činitel sníží vstupní impedance a v případě sériového zapojení se impedance tímto činitelem násobí. Impedance, která je modifikována zpětnou vazbou, je však impedance zesilovače na obrázku 5 s vypnutou zpětnou vazbou a zahrnuje modifikace impedance způsobené rezistory zpětnovazební sítě.
Takže vstupní impedance, kterou vidí zdroj s vypnutou zpětnou vazbou, je Rin = R1 = R11 // RB // rπ1, a se zapnutou zpětnou vazbou (ale bez zpětné vazby)
R i n = R 1 1 + β F B A O L , {\displaystyle R_{\mathrm {in} }={\frac {R_{1}}{1+{\beta }_{\mathrm {FB}}} }A_{\mathrm {OL} }}} ,}

kde se používá dělení, protože vstupní zapojení je boční: zpětnovazební dvouport je paralelní se zdrojem signálu na vstupní straně zesilovače. Připomínka: AOL je výše zjištěné zesílení v otevřené smyčce při zatížení, upravené rezistory sítě zpětné vazby.
O impedanci, kterou vidí zátěž, je třeba dále diskutovat. Zátěž na obrázku 5 je připojena ke kolektoru výstupního tranzistoru, a proto je od těla zesilovače oddělena nekonečnou impedancí výstupního zdroje proudu. Proto zpětná vazba nemá žádný vliv na výstupní impedanci, která zůstává jednoduše RC2, jak je vidět na zátěžovém odporu RL na obrázku 3.
Pokud bychom místo toho chtěli zjistit impedanci prezentovanou na emitoru výstupního tranzistoru (místo na jeho kolektoru), který je sériově připojen ke zpětnovazební síti, zpětná vazba by tento odpor zvýšila o činitel zlepšení ( 1 + βFB AOL).
Zátěžové napětí a zátěžový proudUpravit
Zesílení odvozené výše je proudové zesílení na kolektoru výstupního tranzistoru. Abychom toto zesílení vztáhli k zesílení při napětí na výstupu zesilovače, všimněte si, že výstupní napětí při zátěži RL souvisí s kolektorovým proudem podle Ohmova zákona jako vL = iC (RC2 || RL). Z toho vyplývá, že tranzistorové zesílení vL / iS se zjistí vynásobením proudového zesílení koeficientem RC2 || RL:
v L i S = A F B ( R C 2 ∥ R L ) . {\displaystyle {\frac {v_{\mathrm {L} }}{i_{\mathrm {S} }}}=A_{\mathrm {FB} }(R_{\mathrm {C2} }\paralelní R_{\mathrm {L} })\ .}

Podobně, pokud se za výstup zesilovače považuje proud v zatěžovacím rezistoru RL, proudové dělení určuje zatěžovací proud a zesílení je pak:
i L i S = A F B R C 2 R C 2 + R L. {\displaystyle {\frac {i_{\mathrm {L} . }}{i_{\mathrm {S} }}}=A_{\mathrm {FB} }{\frac {R_{\mathrm {C2}}.}. }}{R_{\mathrm {C2} }+R_{\mathrm {L}.. }}}\ .}

Je hlavní blok zesilovače dvouportový? edit

Následují některé nevýhody dvouportového přístupu, určené pozornému čtenáři.
Na obrázku 7 je znázorněno malosignálové schéma s hlavním zesilovačem a zpětnovazebním dvouportem ve vystínovaných rámečcích. Zpětnovazební dvouport splňuje portové podmínky: na vstupním portu vstupuje a vystupuje Iin a stejně tak na výstupu vstupuje a vystupuje Iout.
Je blok hlavního zesilovače také dvouportový? Hlavní zesilovač je zobrazen v horním stínovaném rámečku. Zemní spoje jsou označeny. Obrázek 7 ukazuje zajímavou skutečnost, že hlavní zesilovač nesplňuje podmínky portů na svém vstupu a výstupu, pokud nejsou zemní spojení zvolena tak, aby se tak stalo. Například na vstupní straně je proud vstupující do hlavního zesilovače IS. Tento proud se rozděluje třemi způsoby: do sítě zpětné vazby, do předřadného odporu RB a do odporu báze vstupního tranzistoru rπ. Aby byla splněna podmínka portu pro hlavní zesilovač, musí být všechny tři složky vráceny na vstupní stranu hlavního zesilovače, což znamená, že musí být připojeny všechny zemnicí vodiče označené G1 a také emitorový vodič GE1. Stejně tak na výstupní straně musí být připojeny všechny zemnicí přívody G2 a také zemnicí přívod GE2. Ve spodní části schématu, pod dvouportovou zpětnou vazbou a mimo bloky zesilovače, je pak G1 připojen k G2. To nutí zemní proudy rozdělit mezi vstupní a výstupní stranu podle plánu. Všimněte si, že toto uspořádání zapojení rozděluje emitor vstupního tranzistoru na stranu báze a stranu kolektoru – to je fyzikálně nemožné, ale elektricky obvod vnímá všechna zemní spojení jako jeden uzel, takže tato fikce je povolena.
Způsob zapojení zemních vodičů samozřejmě pro zesilovač neznamená žádný rozdíl (všechny jsou jedním uzlem), ale pro podmínky na portu ano. Tato umělost je slabinou tohoto přístupu: podmínky na portech jsou potřebné pro zdůvodnění metody, ale obvod ve skutečnosti není ovlivněn tím, jak jsou proudy vyměňovány mezi zemními spoji.
Jestliže však žádné možné uspořádání zemních podmínek nevede k podmínkám na portech, obvod se nemusí chovat stejně. Faktory zlepšení (1 + βFB AOL) pro určení vstupní a výstupní impedance by nemusely fungovat. Tato situace je nepříjemná, protože neúspěch při vytváření dvouportů může odrážet skutečný problém (prostě to není možné), nebo odrážet nedostatek představivosti (například jen nenapadlo rozdělit emitorový uzel na dva). V důsledku toho je při pochybnostech o podmínkách portu možné stanovit, zda jsou činitele zlepšení přesné, přinejmenším dvěma způsoby: buď simulovat příklad pomocí Spice a porovnat výsledky s použitím činitele zlepšení, nebo vypočítat impedanci pomocí zkušebního zdroje a porovnat výsledky.
Praktičtější volbou je zcela upustit od dvouportového přístupu a použít různé alternativy založené na teorii grafů toku signálu, včetně Rosenstarkovy metody, Chomovy metody a použití Blackmanova teorému. Tuto volbu lze doporučit, pokud jsou modely zařízení s malými signály složité nebo nejsou k dispozici (například zařízení jsou známa pouze numericky, třeba z měření nebo ze simulací SPICE).
.