#InsideRL
V typickém problému Reinforcement Learning (RL) existuje učící se a rozhodující se subjekt zvaný agent a okolí, s nímž interaguje, se nazývá prostředí. Okolí na oplátku poskytuje odměny a nový stav na základě akcí agenta. V posilovacím učení tedy neučíme agenta, jak má něco dělat, ale předkládáme mu odměny, ať už pozitivní, nebo negativní, na základě jeho akcí. Naše základní otázka pro tento blog tedy zní, jak matematicky formulujeme jakýkoli problém v RL. K tomu slouží Markovův rozhodovací proces(MDP).

Než odpovíme na naši základní otázku, tj. Jak matematicky formulujeme problémy RL (pomocí MDP), musíme rozvinout naši intuici o :
- Vztah agenta a prostředí
- Markovova vlastnost
- Markovův proces a Markovovy řetězce
- Markovův proces odměňování (MRP)
- Bellmanova rovnice
- Markovův proces odměňování
Vezměte si kávu a nepřestávejte, dokud nebudete hrdí!🧐
Vztah agent-prostředí
Nejprve se podívejme na některé formální definice :
Agent : Softwarové programy, které činí inteligentní rozhodnutí a jsou učícími se v RL. Tito agenti interagují s prostředím pomocí akcí a na základě svých akcí dostávají odměny.
Prostředí :Je to ukázka problému, který má být řešen. nyní můžeme mít reálné prostředí nebo simulované prostředí, se kterým bude náš agent interagovat.

Stav : Jedná se o pozici agentů v určitém časovém kroku v prostředí. kdykoli tedy agent provede nějakou akci, prostředí mu poskytne odměnu a nový stav, do kterého se agent provedením akce dostal.
Vše, co agent nemůže libovolně změnit, je považováno za součást prostředí. Zjednodušeně řečeno, akce může být jakékoli rozhodnutí, které chceme, aby se agent naučil, a stav může být cokoli, co může být užitečné při výběru akcí. Nepředpokládáme, že vše v prostředí je agentovi neznámé, například výpočet odměny je považován za součást prostředí, i když agent ví něco málo o tom, jak se jeho odměna počítá v závislosti na jeho akcích a stavech, ve kterých je provádí. Je to proto, že odměny nemůže agent libovolně měnit. Někdy může agent plně znát své prostředí, ale přesto je pro něj obtížné maximalizovat odměnu, podobně jako můžeme vědět, jak hrát Rubikovu kostku, ale přesto ji nedokážeme vyřešit. Můžeme tedy s jistotou říci, že vztah agent – prostředí představuje hranici ovládání agenta, nikoli jeho znalosti.
Markovova vlastnost
Přechod : Přechod z jednoho stavu do druhého se nazývá přechod.
Pravděpodobnost přechodu: Pravděpodobnost, že agent přejde z jednoho stavu do druhého, se nazývá pravděpodobnost přechodu.
Markovova vlastnost říká, že :
„Budoucnost je nezávislá na minulosti dané přítomností“
Matematicky můžeme toto tvrzení vyjádřit jako :
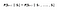
S označuje současný stav agenta a s označuje příští stav. Tato rovnice znamená, že přechod ze stavu S do S je zcela nezávislý na minulosti. RHS rovnice tedy znamená totéž co LHS, pokud má systém Markovovu vlastnost. Intuitivně to znamená, že náš současný stav již zachycuje informace o minulých stavech.
Pravděpodobnost přechodu stavu :
Jak nyní víme o pravděpodobnosti přechodu, můžeme definovat pravděpodobnost přechodu stavu takto :
Pro Markovův stav z S do S tj. libovolný jiný následný stav , je pravděpodobnost přechodu stavu dána vztahem

Pravděpodobnost přechodu stavu můžeme formulovat do matice pravděpodobnosti přechodu stavu podle :

Každý řádek matice představuje pravděpodobnost z přechodu z našeho původního nebo výchozího stavu do některého následného stavu.Součet každého řádku je roven 1.
Markovův proces neboli Markovovy řetězce
Markovův proces je náhodný proces bez paměti, tj. posloupnost náhodného stavu S,S,….S s Markovovou vlastností. je to tedy v podstatě posloupnost stavů s Markovovou vlastností. lze ji definovat pomocí množiny stavů(S) a matice pravděpodobnosti přechodu (P).Dynamiku prostředí lze plně definovat pomocí množiny stavů(S) a matice pravděpodobnosti přechodu(P).
Ale co znamená náhodný proces ?
Pro odpověď na tuto otázku se podívejme na příklad:
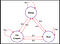
Hrany stromu označují pravděpodobnost přechodu. Z tohoto řetězce vybereme nějaký vzorek. Nyní předpokládejme, že jsme spali a podle rozdělení pravděpodobnosti existuje 0,6 šance, že poběžíme, a 0,2 šance, že budeme spát dál, a opět 0,2, že budeme jíst zmrzlinu. Podobně si můžeme představit další posloupnosti, které můžeme z tohoto řetězce vzorkovat.
Některé vzorky z řetězce :
- Spánek – Běh – Zmrzlina – Spánek
- Spánek – Zmrzlina – Zmrzlina – Běh
Ve výše uvedených dvou posloupnostech vidíme, že při každém spuštění řetězce dostaneme náhodnou množinu stavů(S) (tj. Spánek,Zmrzlina,Spánek ).Doufám, že je nyní jasné, proč se Markovův proces nazývá náhodná množina posloupností.
Než přejdeme k Markovovu procesu odměn, podívejme se na některé důležité pojmy, které nám pomohou v pochopení MRP.
Odměny jsou číselné hodnoty, které agent obdrží při provedení nějaké akce v určitém stavu (stavech) v prostředí. Číselná hodnota může být kladná nebo záporná na základě akcí agenta.
Při učení posilováním se staráme o maximalizaci kumulativní odměny (všechny odměny, které agent obdrží z prostředí) namísto, odměny, kterou agent obdrží z aktuálního stavu(také se nazývá okamžitá odměna). Tento celkový součet odměn, které agent obdrží z prostředí, se nazývá výnosy.
Výnosy můžeme definovat jako :
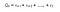
r je odměna, kterou agent obdržel v časovém kroku t při provádění akce(a) pro přechod z jednoho stavu do druhého. Podobně r je odměna, kterou agent obdržel v časovém kroku t při provedení akce (akce) k přesunu do jiného stavu. A r je odměna, kterou agent obdrží v posledním časovém kroku t provedením akce pro přesun do jiného stavu.
Episodické a kontinuální úlohy
Episodické úlohy: Můžeme říci, že mají konečné stavy. Například v závodních hrách spustíme hru (odstartujeme závod) a hrajeme ji, dokud hra neskončí (závod skončí!). Tomu se říká epizoda. Jakmile hru znovu spustíme, začne z počátečního stavu, a proto je každá epizoda nezávislá.
Spojité úlohy : Jsou to úlohy, které nemají žádný konec, tj. nemají žádný koncový stav. tyto typy úloh nikdy neskončí. například Učíme se programovat!“
Nyní je snadné vypočítat návratnost epizodických úloh, protože ty nakonec skončí, ale co souvislé úlohy, protože ty budou pokračovat donekonečna. Výnosy z sečtou do nekonečna! Jak tedy definujeme výnosy u spojitých úloh?
Tady potřebujeme diskontní faktor (ɤ).
Diskontní faktor (ɤ): Určuje, jak velký význam má být přikládán okamžité odměně a budoucím odměnám. V podstatě nám pomáhá vyhnout se nekonečnu jako odměně v průběžných úlohách. Má hodnotu mezi 0 a 1. Hodnota 0 znamená, že větší význam se přikládá okamžité odměně, a hodnota 1 znamená, že větší význam se přikládá budoucím odměnám. V praxi se diskontní faktor s hodnotou 0 nikdy nenaučíme, protože bere v úvahu pouze okamžitou odměnu, a diskontní faktor s hodnotou 1 bude pokračovat u budoucích odměn, což může vést k nekonečnu. Proto se optimální hodnota diskontního faktoru pohybuje mezi 0,2 a 0,8.
Výnosy pomocí diskontního faktoru tedy můžeme definovat takto :(Řekněme, že se jedná o rovnici 1 ,protože tuto rovnici budeme později používat pro odvození Bellmanovy rovnice)

Pochopíme to na příkladu,Předpokládejme, že žijete na místě, kde se potýkáte s nedostatkem vody, takže pokud k vám někdo přijde a řekne, že vám dá 100 litrů vody!(předpokládejte prosím!) za příštích 15 hodin jako funkci nějakého parametru (ɤ). podívejme se na dvě možnosti : (Řekněme, že je to rovnice 1 , protože tuto rovnici budeme později používat pro odvození Bellmanovy rovnice)
Jedna s diskontním faktorem (ɤ) 0. Druhá s diskontním faktorem (ɤ) 0.8 :
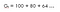
To znamená, že bychom měli počkat do 15. hodiny, protože pokles není příliš výrazný , takže se stále vyplatí jít až na konec. to znamená, že nás zajímají i budoucí odměny.Pokud je tedy diskontní faktor blízký 1, pak se budeme snažit jít až do konce, protože odměny mají značný význam.
Druhá varianta s diskontním faktorem (ɤ) 0,2 :
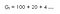
To znamená, že nás více zajímají brzké odměny, protože odměny se v hodině výrazně snižují, takže bychom nemuseli chtít čekat až do konce (do 15. hodiny), protože by to bylo bezcenné. pokud je tedy diskontní faktor blízký nule, pak jsou důležitější okamžité odměny než budoucí.
Takže jakou hodnotu diskontního faktoru použít ?
Záleží na úloze, pro kterou chceme agenta vycvičit. Předpokládejme, že v šachové hře je cílem porazit soupeřova krále. Pokud budeme přikládat důležitost okamžitým odměnám, jako je odměna při porážce pěšce jakéhokoli soupeřova hráče, pak se agent naučí plnit tyto dílčí cíle bez ohledu na to, zda budou poraženi i jeho hráči. V této úloze jsou tedy důležitější budoucí odměny. V některých případech můžeme dát přednost okamžitým odměnám, jako například v příkladu s vodou, který jsme viděli dříve.
Markovův proces odměňování
Do této chvíle jsme viděli, jak Markovův řetězec definuje dynamiku prostředí pomocí množiny stavů (S) a matice pravděpodobnosti přechodu (P).Víme však, že při učení posilováním jde o cíl maximalizovat odměnu.Přidejme tedy odměnu do našeho Markovova řetězce.Tím získáme Markovův proces odměňování.
Markovův proces odměňování : Jak název napovídá, MDP jsou Markovovy řetězce s úsudkem o hodnotách. v podstatě z každého stavu, ve kterém se náš agent nachází, získáme hodnotu.
Matematicky definujeme Markov Reward Process jako :
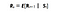
Co tato rovnice znamená, je, kolik odměny (Rs) dostaneme z určitého stavu S. To nám říká okamžitou odměnu z daného stavu, ve kterém se náš agent nachází. Jak tyto odměny maximalizujeme z každého stavu, ve kterém se náš agent nachází, uvidíme v dalším příběhu. Zjednodušeně řečeno, maximalizujeme kumulativní odměnu, kterou získáme z každého stavu.
Definujeme MRP jako (S,P,R,ɤ) ,kde :
- S je množina stavů,
- P je matice pravděpodobnosti přechodu,
- R je funkce odměny , kterou jsme viděli dříve,
- ɤ je diskontní faktor
Markovův rozhodovací proces
Nyní rozvineme naši intuici pro Bellmanovu rovnici a Markovův rozhodovací proces.
Politická funkce a hodnotová funkce
Hodnotová funkce určuje, jak dobré je pro agenta být v určitém stavu. Aby bylo možné určit, jak dobré bude být v určitém stavu, musí to samozřejmě záviset na nějakých akcích, které bude provádět. Zde přichází na řadu politika. Politika určuje, jaké akce má agent provádět v určitém stavu s.

Politika je jednoduchá funkce, která pro každý stav (s ∈ S) definuje rozdělení pravděpodobnosti nad akcemi (a∈ A). Pokud se agent v čase t řídí politikou π, pak π(a|s) je pravděpodobnost, že agent s provede akci (a ) v konkrétním časovém kroku (t). při učení posilováním rozhodují o změně politiky zkušenosti agenta. Matematicky je politika definována takto :
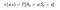
Nyní, jak zjistíme hodnotu stavu.Hodnota stavu s, kdy agent sleduje politiku π, kterou označíme vπ(s), je očekávaný výnos počínaje stavem s a sledováním politiky π pro další stavy,dokud nedosáhneme konečného stavu.Můžeme ji formulovat jako : (Tato funkce se také nazývá funkce hodnoty stavu)

Tato rovnice nám dává očekávaný výnos počínaje stavem(s) a následným přechodem do následných stavů s politikou π. Je třeba si uvědomit, že výnosy, které dostaneme, jsou stochastické, zatímco hodnota stavu stochastická není. Je to očekávání výnosů z počátečního stavu s a následně do jakéhokoli jiného stavu. A také si všimněte, že hodnota konečného stavu (pokud nějaký existuje) je nulová. Podívejme se na příklad :
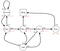
Předpokládejme, že náš počáteční stav je třída 2 a přejdeme do třídy 3, pak Pass a pak Sleep. zkrátka třída 2 > třída 3 > Pass > Sleep.
Náš očekávaný výnos je s diskontním faktorem 0,5:
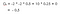
Poznámka:Je to -2 + (-2 * 0.5) + 10 * 0,25 + 0 místo -2 * -2 * 0,5 + 10 * 0,25 + 0.Pak hodnota třídy 2 je -0,5 .
Bellmanova rovnice pro hodnotovou funkci
Bellmanova rovnice nám pomáhá najít optimální politiku a hodnotovou funkci.Víme, že naše politika se mění se zkušenostmi, takže budeme mít různé hodnotové funkce podle různých politik.Optimální hodnotová funkce je taková, která dává maximální hodnotu ve srovnání se všemi ostatními hodnotovými funkcemi.
Bellmanova rovnice říká, že hodnotovou funkci lze rozložit na dvě části:
- Mimořádná odměna, R
- Diskontovaná hodnota následných stavů,
Matematicky můžeme Bellmanovu rovnici definovat jako :

Pochopíme, co tato rovnice říká, pomocí příkladu :
Předpokládejme, že existuje robot v nějakém stavu (s) a pak se z tohoto stavu přesune do nějakého jiného stavu (s‘). Nyní je otázkou, jak dobré bylo pro robota být v daném stavu (s). Pomocí Bellmanovy rovnice můžeme říci, že je to očekávání odměny, kterou dostal při opuštění stavu(s), plus hodnota stavu (s‘), do kterého se přesunul.
Podívejme se na další příklad :
Chceme znát hodnotu stavu s.Hodnota stavu(ů) je odměna, kterou jsme dostali při opuštění tohoto stavu, plus diskontovaná hodnota stavu, na kterém jsme přistáli, vynásobená pravděpodobností přechodu, že do něj přejdeme.
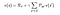
Výše uvedenou rovnici lze vyjádřit v maticovém tvaru takto :

Kde v je hodnota stavu, ve kterém jsme se nacházeli, která je rovna okamžité odměně plus diskontované hodnotě následujícího stavu vynásobené pravděpodobností přechodu do tohoto stavu.
Složitost běhu tohoto výpočtu je O(n³). Proto je zřejmé, že toto řešení není praktické pro řešení větších MRP (totéž platí i pro MDP). v dalších blozích se budeme zabývat efektivnějšími metodami, jako je dynamické programování (iterace hodnot a iterace politik), metody Monte-Claro a TD-Learning.
O Bellmanově rovnici budeme hovořit mnohem podrobněji v příštím povídání.
Co je to Markovův rozhodovací proces?
Markovův rozhodovací proces : Je to Markovův proces odměňování s rozhodnutími.Vše je stejné jako u MRP, ale nyní máme skutečný děj, který rozhoduje nebo provádí akce.
Je to trojice (S, A, P, R, 𝛾), kde:
- S je množina stavů,
- A je množina akcí, které může agent zvolit,
- P je matice pravděpodobnosti přechodu,
- R je odměna nashromážděná za akce agenta,
- 𝛾 je diskontní faktor.
P a R se budou mírně měnit v závislosti na akcích takto :
Matice pravděpodobnosti přechodu
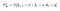
Funkce odměny
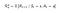
Nyní je naše funkce odměny závislá na akci.
Dosud jsme hovořili o získání odměny (r), když náš agent projde množinou stavů (s) podle politiky π.Ve skutečnosti je v Markovově rozhodovacím procesu (MDP) politika mechanismus rozhodování.
Máme tedy nyní mechanismus, který se rozhodne pro nějakou akci.
Politika v MDP závisí na aktuálním stavu. nezávisí na historii. to je Markovova vlastnost. aktuální stav, ve kterém se nacházíme, tedy charakterizuje historii.
Již jsme viděli, jak dobré je pro agenta být v určitém stavu (funkce hodnoty stavu). nyní se podívejme, jak dobré je provést určitou akci podle politiky π ze stavu s (funkce hodnoty akce).
Funkce hodnoty stavu a akce neboli Q-Funkce
Tato funkce udává, jak dobré je pro agenta provést akci (a) ve stavu (s) s politikou π.
Matematicky můžeme funkci hodnoty stavu-akce definovat jako :

Základně nám říká, jakou hodnotu má provedení určité akce (a) ve stavu (s) s politikou π.
Podívejme se na příklad Markovova rozhodovacího procesu :
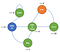
Nyní vidíme, že již neexistují žádné pravděpodobnosti.Ve skutečnosti má nyní náš agent na výběr, například po probuzení ,si můžeme vybrat, zda se budeme dívat na netflix, nebo zda budeme kódovat a ladit. samozřejmě akce agenta jsou definovány w.r.t nějakou politikou π a podle toho dostane odměnu.