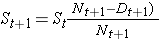Často nás zajímá, zda existují rozdíly v přežití (nebo kumulativním výskytu událostí) mezi různými skupinami účastníků. Například v klinickém hodnocení s výsledkem přežití nás může zajímat porovnání přežití mezi účastníky, kteří dostávají nový lék, ve srovnání s placebem (nebo standardní léčbou). V observační studii nás může zajímat srovnání přežití mezi muži a ženami nebo mezi účastníky s určitým rizikovým faktorem a bez něj (např. hypertenze nebo diabetes). Pro porovnání přežití mezi nezávislými skupinami je k dispozici několik testů.
Test log rank
Test log rank je oblíbený test pro testování nulové hypotézy o neexistenci rozdílu v přežití mezi dvěma nebo více nezávislými skupinami. Test porovnává celou zkušenost přežití mezi skupinami a lze si jej představit jako test, zda jsou křivky přežití shodné (překrývají se), nebo ne. Křivky přežití se odhadují pro každou skupinu posuzovanou samostatně pomocí Kaplanovy-Meierovy metody a statisticky se porovnávají pomocí logaritmického testu. Je důležité poznamenat, že existuje několik variant statistiky log rank testu, které jsou implementovány různými statistickými výpočetními balíky (např. SAS, R 4,6). Zde uvádíme jednu z verzí, která úzce souvisí s testovou statistikou chí-kvadrát a porovnává pozorované a očekávané počty příhod v každém časovém bodě během sledovaného období.
Příklad:
Probíhá malá klinická studie, která porovnává dvě kombinace léčby u pacientů s pokročilým karcinomem žaludku. Dvaceti účastníkům s karcinomem žaludku ve stadiu IV, kteří souhlasí s účastí ve studii, je náhodně přidělena chemoterapie před operací nebo chemoterapie po operaci. Primárním výsledkem je úmrtí a účastníci jsou sledováni po dobu až 48 měsíců (4 roky) od zařazení do studie. Zkušenosti účastníků v jednotlivých ramenech studie jsou uvedeny níže.
|
Chemoterapie před operací |
|
Chemoterapie po operaci |
||
|---|---|---|---|---|
|
Měs. Úmrtí |
Měsíc posledního kontaktu |
|
Měsíc úmrtí |
Měsíc posledního kontaktu |
|
8 |
8 |
|
33 |
48 |
|
12 |
32 |
|
28 |
48 |
|
26 |
20 |
|
41 |
25 |
|
14 |
40 |
|
|
37 |
|
21 |
|
|
|
48 |
|
27 |
|
|
|
25 |
|
|
|
|
|
43 |
Šest účastníků ve skupině s chemoterapií před operací v průběhu sledování zemřelo.v porovnání se třemi účastníky ve skupině s chemoterapií po operaci. Ostatní účastníci v jednotlivých skupinách jsou sledováni různý počet měsíců, někteří až do konce studie ve 48 měsících (ve skupině s chemoterapií po operaci). Pomocí výše uvedených postupů nejprve sestavíme tabulky životnosti pro každou léčebnou skupinu pomocí Kaplanovy-Meierovy metody.
Tabulka životnosti pro skupinu dostávající chemoterapii před operací
|
Čas, Měsíce |
Počet ohrožených Nt |
Počet úmrtí Dt |
Počet cenzurovaných Ct |
Pravděpodobnost přežití
|
|---|---|---|---|---|
|
0 |
10 |
|
|
1 |
|
8 |
10 |
1 |
1 |
0.900 |
|
12 |
8 |
1 |
|
0.788 |
|
14 |
7 |
1 |
|
0.675 |
|
20 |
6 |
|
1 |
0.675 |
|
21 |
5 |
1 |
|
0.540 |
|
26 |
4 |
1 |
|
0.405 |
|
27 |
3 |
1 |
|
0.270 |
|
32 |
2 |
|
1 |
0.270 |
|
40 |
1 |
|
1 |
0.270 |
Tabulka životnosti pro skupinu dostávající chemoterapii po operaci
|
Čas, Měsíce |
Počet ohrožených Nt |
Počet zemřelých Dt |
Počet cenzurovaných Ct |
Pravděpodobnost přežití
|
|---|---|---|---|---|
|
0 |
10 |
|
|
1 |
|
25 |
10 |
|
2 |
1.000 |
|
28 |
8 |
1 |
|
0.875 |
|
33 |
7 |
1 |
|
0.750 |
|
37 |
6 |
|
1 |
0.750 |
|
41 |
5 |
1 |
|
0.600 |
|
43 |
4 |
|
1 |
0.600 |
|
48 |
3 |
|
3 |
0,600 |
Dvě křivky přežití jsou uvedeny níže.
Křivky přežití v každé léčebné skupině
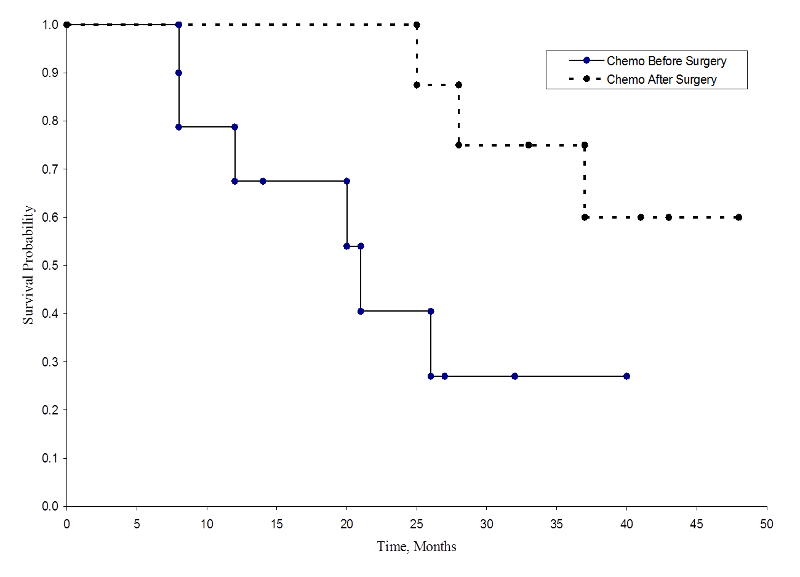
Pravděpodobnosti přežití pro skupinu s chemoterapií po operaci jsou vyšší než pravděpodobnosti přežití pro skupinu s chemoterapií před operací, což naznačuje přínos pro přežití. Tyto křivky přežití jsou však odhadovány z malých vzorků. Pro porovnání přežití mezi skupinami můžeme použít logaritmický test. Nulová hypotéza zní, že mezi oběma skupinami není rozdíl v přežití nebo že mezi populacemi není rozdíl v pravděpodobnosti úmrtí v kterémkoli bodě. Log rank test je neparametrický test a nečiní žádné předpoklady o rozděleních přežití. V podstatě log rank test porovnává pozorovaný počet událostí v každé skupině s tím, co by se očekávalo, kdyby platila nulová hypotéza (tj, kdyby křivky přežití byly identické).
H0: Obě křivky přežití jsou identické (nebo S1t = S2t) versus H1: Obě křivky přežití nejsou identické (nebo S1t ≠ S2t, v libovolném čase t) (α=0,05).
Statistika log rank je přibližně rozdělena jako testovací statistika chí-kvadrát. Existuje několik forem této testové statistiky a liší se způsobem výpočtu. Používáme následující:
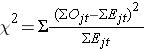
kde ΣOjt představuje součet pozorovaného počtu událostí v j-té skupině v čase (např. j=1,2) a ΣEjt představuje součet očekávaného počtu událostí v j-té skupině v čase.
Součty pozorovaného a očekávaného počtu událostí se počítají pro každý čas události a sčítají se pro každou srovnávací skupinu. Logaritmická statistika má stupně volnosti rovny k-1, kde k představuje počet srovnávacích skupin. V tomto příkladu je k=2, takže testovací statistika má 1 stupeň volnosti.
Pro výpočet testovací statistiky potřebujeme pozorovaný a očekávaný počet událostí v každém čase události. Pozorovaný počet událostí je ze vzorku a očekávaný počet událostí se vypočítá za předpokladu, že platí nulová hypotéza (tj. že křivky přežití jsou identické).
Pro vytvoření očekávaného počtu událostí uspořádáme data do tabulky životnosti s řádky představujícími každý čas události bez ohledu na skupinu, ve které k události došlo. Sledujeme také přiřazení ke skupině. Poté odhadneme podíl událostí, které se vyskytnou v každém čase (Ot/Nt), pomocí údajů z obou skupin dohromady za předpokladu, že není rozdíl v přežití (tj. za předpokladu, že platí nulová hypotéza). Tyto odhady vynásobíme počtem ohrožených účastníků v daném čase v každé ze srovnávacích skupin (N1t a N2t pro skupiny 1 a 2).
Konkrétně vypočítáme pro každý čas události t počet ohrožených v každé skupině, Njt (např. kde j označuje skupinu, j=1, 2) a počet událostí (úmrtí), Ojt ,v každé skupině. Následující tabulka obsahuje informace potřebné k provedení logaritmického testu k porovnání výše uvedených křivek přežití. Skupina 1 představuje skupinu s chemoterapií před operací a skupina 2 představuje skupinu s chemoterapií po operaci.
Údaje pro Log Rank test k porovnání křivek přežití
|
Čas, Měsíce |
Počet ohrožených ve skupině 1
N1t |
Počet ohrožených ve skupině 2
N2t |
Počet událostí (úmrtí) ve skupině 1
O1t |
Počet Událostí (úmrtí) ve skupině 2
O2t |
|---|---|---|---|---|
|
8 |
10 |
10 |
1 |
0 |
|
12 |
8 |
10 |
1 |
0 |
|
14 |
7 |
10 |
1 |
0 |
|
21 |
5 |
10 |
1 |
0 |
|
26 |
4 |
8 |
1 |
0 |
|
27 |
3 |
8 |
1 |
0 |
|
28 |
2 |
8 |
0 |
1 |
|
33 |
1 |
7 |
0 |
1 |
|
41 |
0 |
5 |
0 |
1 |
Dále sečteme rizikový počet, Nt = N1t+N2t, v každém čase události a počet pozorovaných událostí (úmrtí), Ot = O1t+O2t, v každém čase události. Poté vypočítáme očekávaný počet událostí v každé skupině. Očekávaný počet událostí se vypočítá v každém čase události takto:
E1t = N1t*(Ot/Nt) pro skupinu 1 a E2t = N2t*(Ot/Nt) pro skupinu 2. Výpočty jsou uvedeny v následující tabulce.
Očekávané počty událostí v každé skupině
|
Čas, Měsíce |
Počet ohrožených ve skupině 1 N1t |
Počet ohrožených ve skupině 2 N2t |
Celkový počet ohrožených Nt . |
Počet událostí ve skupině 1 O1t |
Počet událostí ve skupině 2 O2t |
Celkový počet událostí Ot |
Očekávaný počet událostí ve skupině 1 E1t = N1t*(Ot/Nt) |
Očekávaný počet událostí ve skupině 2 E2t = N2t*(Ot/Nt) |
|---|---|---|---|---|---|---|---|---|
|
8 |
10 |
10 |
20 |
1 |
0 |
1 |
0.500 |
0.500 |
|
12 |
8 |
10 |
18 |
1 |
0 |
1 |
0.444 |
0.556 |
|
14 |
7 |
10 |
17 |
1 |
0 |
1 |
0.412 |
0.588 |
|
21 |
5 |
10 |
15 |
1 |
0 |
1 |
0.333 |
0.667 |
|
26 |
4 |
8 |
12 |
1 |
0 |
1 |
0.333 |
0.667 |
|
27 |
3 |
8 |
11 |
1 |
0 |
1 |
0.273 |
0.727 |
|
28 |
2 |
8 |
10 |
0 |
1 |
1 |
0.200 |
0.800 |
|
33 |
1 |
7 |
8 |
0 |
1 |
1 |
0.125 |
0.875 |
|
41 |
0 |
5 |
5 |
0 |
1 |
1 |
0.000 |
1.000 |
Dále sečteme pozorované počty událostí v každé skupině (∑O1t a ΣO2t) a očekávané počty událostí v každé skupině (ΣE1t a ΣE2t) v čase. Ty jsou uvedeny ve spodním řádku další tabulky níže.
Celkové pozorované a očekávané počty pozorovaných událostí v každé skupině
|
Čas, Měsíce |
Počet ohrožených ve skupině 1 N1t |
Počet ohrožených ve skupině 2 N2t |
Celkový počet ohrožených Nt . |
Počet událostí ve skupině 1 O1t |
Počet událostí ve skupině 2 O2t |
Celkový počet událostí Ot |
Očekávaný počet událostí ve skupině 1 E1t = N1t*(Ot/Nt) |
Očekávaný počet událostí ve skupině 2 E2t = N2t*(Ot/Nt) |
|---|---|---|---|---|---|---|---|---|
|
8 |
10 |
10 |
20 |
1 |
0 |
1 |
0.500 |
0.500 |
|
12 |
8 |
10 |
18 |
1 |
0 |
1 |
0.444 |
0.556 |
|
14 |
7 |
10 |
17 |
1 |
0 |
1 |
0.412 |
0.588 |
|
21 |
5 |
10 |
15 |
1 |
0 |
1 |
0.333 |
0.667 |
|
26 |
4 |
8 |
12 |
1 |
0 |
1 |
0.333 |
0.667 |
|
27 |
3 |
8 |
11 |
1 |
0 |
1 |
0.273 |
0.727 |
|
28 |
2 |
8 |
10 |
0 |
1 |
1 |
0.200 |
0.800 |
|
33 |
1 |
7 |
8 |
0 |
1 |
1 |
0.125 |
0.875 |
|
41 |
0 |
5 |
5 |
0 |
1 |
1 |
0.000 |
1.000 |
|
|
6 |
3 |
|
2.620 |
6,380 |
Nyní můžeme vypočítat testovací statistiku:
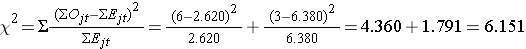
Testovací statistika je přibližně rozdělena jako chí-kvadrát s 1 stupněm volnosti. Kritickou hodnotu testu tedy nalezneme v tabulce Kritické hodnoty rozdělení Χ2.
Pro tento test platí rozhodovací pravidlo: Zamítnout H0, jestliže Χ2 > 3,84. V případě, že H0 > 3,84, je třeba zamítnout H0. Pozorujeme, že Χ2 = 6,151, což překračuje kritickou hodnotu 3,84. Proto H0 zamítáme. Máme významný důkaz, α=0,05, který ukazuje, že obě křivky přežití se liší.
Příklad:
Výzkumník chce vyhodnotit účinnost krátké intervence k prevenci konzumace alkoholu v těhotenství. Těhotné ženy s anamnézou silné konzumace alkoholu jsou zařazeny do studie a náhodně vybrány buď ke krátké intervenci zaměřené na abstinenci od alkoholu, nebo ke standardní prenatální péči. Sledovaným výsledkem je recidiva pití alkoholu. Ženy jsou do studie zařazeny přibližně v 18. týdnu těhotenství a jsou sledovány v průběhu těhotenství až do porodu (přibližně 39. týden těhotenství). Údaje jsou uvedeny níže a uvádějí, zda ženy znovu začaly pít, a pokud ano, čas jejich prvního napití měřený počtem týdnů od randomizace. U žen, u nichž k recidivě nedošlo, zaznamenáváme počet týdnů od randomizace, kdy jsou bez alkoholu.
|
Standardní prenatální péče |
|
Krátká intervence |
||
|---|---|---|---|---|
|
Recidiva |
Žádná recidiva |
|
Recidiva |
Žádná recidiva |
|
19 |
20 |
|
16 |
21 |
|
6 |
19 |
|
21 |
15 |
|
5 |
17 |
|
7 |
18 |
|
4 |
14 |
|
|
18 |
|
|
|
|
|
5 |
Zajímavou otázkou je, zda existuje rozdíl v době do relapsu u žen zařazených do standardní prenatální péče ve srovnání s ženami zařazenými do krátké intervence.
- Krok 1.
Stanovte hypotézy a určete hladinu významnosti.
H0: Doba bez relapsu je mezi skupinami stejná oproti
H1: Doba bez relapsu není mezi skupinami stejná (α=0,05)
- Krok 2.
Zvolte vhodnou testovací statistiku.
Testovací statistika pro logaritmický test je
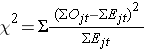
- Krok 3.
Nastavte rozhodovací pravidlo.
Testovací statistika se řídí chí-kvadrát rozdělením, a proto najdeme kritickou hodnotu v tabulce kritických hodnot pro rozdělení Χ2) pro df=k-1=2-1=1 a α=0,05.
Testovací statistika se řídí chí-kvadrát rozdělením. Kritická hodnota je 3,84 a rozhodovací pravidlo zní zamítnout H0, jestliže Χ2 > 3,84.
- Krok 4.
Vypočtěte testovací statistiku.
Pro výpočet testovací statistiky uspořádáme data podle časů událostí (relapsů) a určíme počty ohrožených žen v každé léčebné skupině a počty žen, které relabují v každém sledovaném čase relapsu. V následující tabulce představuje skupina 1 ženy, které dostávají standardní prenatální péči, a skupina 2 ženy, které dostávají krátkou intervenci.
|
Čas, Týdnů |
Počet ohrožených – skupina 1 N1t |
Počet ohrožených – skupina 2 N2t |
Počet relapsů – skupina 1 O1t |
Počet relapsů -. Skupina 2 O2t |
|---|---|---|---|---|
|
4 |
8 |
8 |
1 |
0 |
|
5 |
7 |
8 |
1 |
0 |
|
6 |
6 |
7 |
1 |
0 |
|
7 |
5 |
7 |
0 |
1 |
|
16 |
4 |
5 |
0 |
1 |
|
19 |
3 |
2 |
1 |
0 |
|
21 |
0 |
2 |
0 |
1 |
Dále sečteme ohrožený počet, 
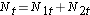, v každém čase události, počet pozorovaných událostí (relapsů), 
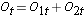, v každém čase události a určíme očekávaný počet relapsů v každé skupině v každém čase události pomocí 
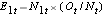a 
.
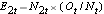Poté sečteme pozorované počty relapsů v každé skupině (ΣO1t a ΣO2t) a očekávané počty relapsů v každé skupině (ΣE1t a ΣE2t) v čase. Výpočty pro údaje v tomto příkladu jsou uvedeny níže.
| Čas, Týdnů |
Počet v rizikové skupině 1 N1t |
Počet v rizikové skupině 2 N2t |
Celkový počet v rizikové skupině Nt |
.
Počet relapsů Skupina 1 O1t |
Počet relapsů Skupina 2 O2t |
Celkový počet relapsu Ot |
Očekávaný počet relapsů ve skupině 1
|
Očekávaný počet relapsů ve skupině 2
|
|---|---|---|---|---|---|---|---|---|
|
4 |
8 |
8 |
16 |
1 |
0 |
1 |
0.500 |
0.500 |
|
5 |
7 |
8 |
15 |
1 |
0 |
1 |
0.467 |
0.533 |
|
6 |
6 |
7 |
13 |
1 |
0 |
1 |
0.462 |
0.538 |
|
7 |
5 |
7 |
12 |
0 |
1 |
1 |
0.417 |
0.583 |
|
16 |
4 |
5 |
9 |
0 |
1 |
1 |
0.444 |
0.556 |
|
19 |
3 |
2 |
5 |
1 |
0 |
1 |
0.600 |
0.400 |
|
21 |
0 |
2 |
2 |
0 |
1 |
1 |
0.000 |
1.000 |
|
|
|
|
|
4 |
3 |
|
2.890 |
4.110 |
Nyní vypočítáme testovací statistiku:
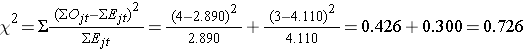
- Krok 5.
Závěr. Nezamítejte H0, protože 0,726 < 3,84. Nemáme statisticky významný důkaz při α=0,05, který by ukazoval, že se doba do recidivy mezi skupinami liší.
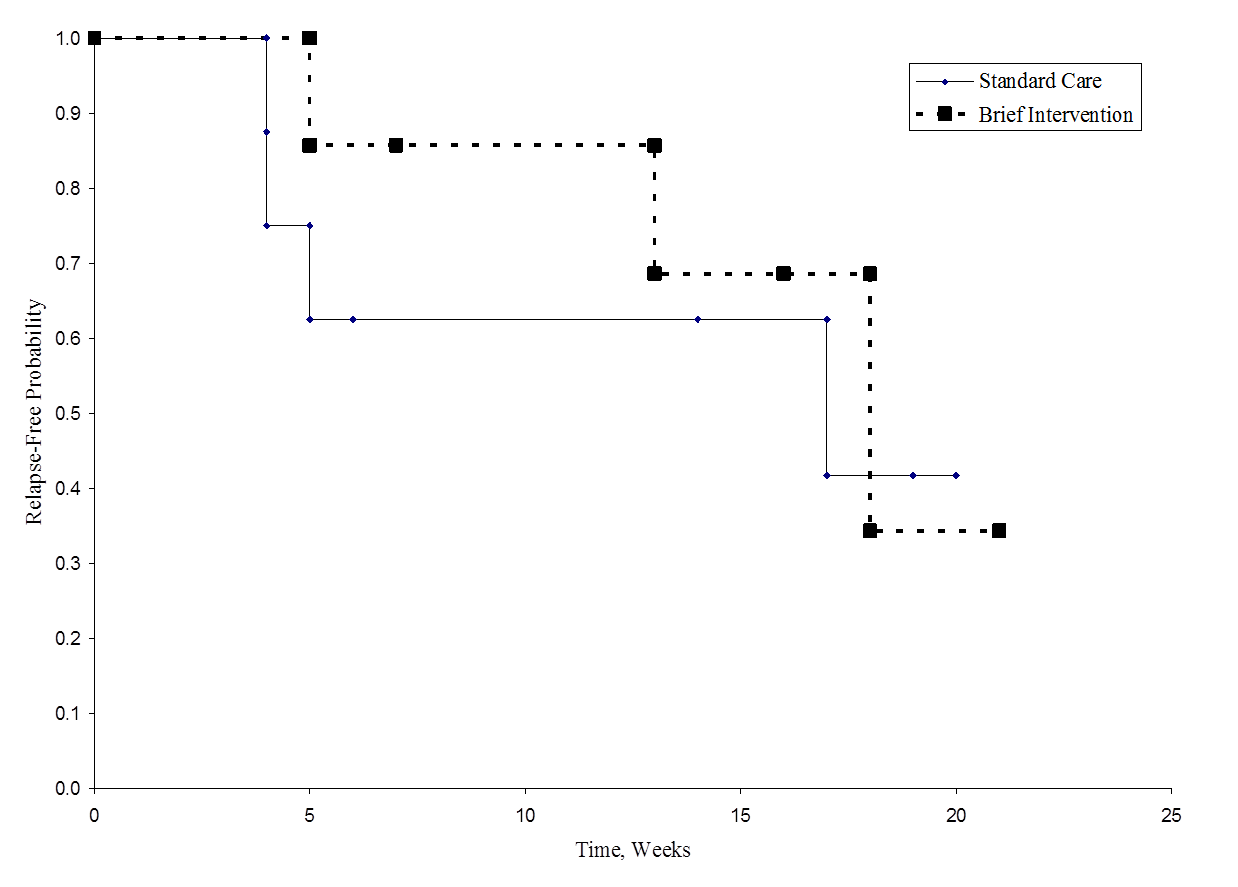
Na obrázku níže je znázorněno přežití (doba bez recidivy) v jednotlivých skupinách. Všimněte si, že křivky přežití nevykazují velké rozdělení, což odpovídá nesignifikantním zjištěním v testu hypotézy.
Doba bez relapsu v každé skupině
Jak bylo uvedeno, existuje několik variant statistiky logaritmu. Některé balíky pro statistické výpočty používají následující testovací statistiku pro log rank test k porovnání dvou nezávislých skupin:
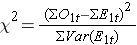
kde ΣO1t je součet pozorovaného počtu událostí ve skupině 1 a ΣE1t je součet očekávaného počtu událostí ve skupině 1 vzatý přes všechny časy událostí. Jmenovatel je součet rozptylů očekávaných počtů událostí v každém čase události, který se vypočítá takto:
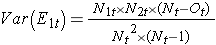
Existují i další verze logaritmické statistiky a také další testy pro porovnání funkcí přežití mezi nezávislými skupinami.7-9 Oblíbeným testem je například modifikovaný Wilcoxonův test, který je citlivý na větší rozdíly v ohrožení na začátku oproti pozdějšímu sledování.10
zpět na začátek | předchozí stránka | další stránka
.