Elektromagnetický metamateriál ovlivňuje elektromagnetické vlny, které dopadají na jeho strukturní prvky, jež jsou menší než vlnová délka, nebo s nimi interagují. Aby se choval jako homogenní materiál přesně popsaný efektivním indexem lomu, musí být jeho prvky mnohem menší než vlnová délka.
Pro mikrovlnné záření jsou prvky v řádu milimetrů. Metamateriály pro mikrovlnné frekvence jsou obvykle konstruovány jako pole elektricky vodivých prvků (například smyček z drátů), které mají vhodné indukční a kapacitní vlastnosti. Mnoho mikrovlnných metamateriálů používá rezonátory s děleným prstencem.
Fotonické metamateriály mají strukturu v měřítku nanometrů a manipulují se světlem na optických frekvencích. Fotonické krystaly a frekvenčně selektivní povrchy, jako jsou difrakční mřížky, dielektrická zrcadla a optické povlaky, vykazují podobnosti se subvlnově strukturovanými metamateriály. Obvykle se však považují za odlišné od metamateriálů, protože jejich funkce vyplývá z difrakce nebo interference, a proto je nelze aproximovat jako homogenní materiál. Materiálové struktury, jako jsou fotonické krystaly, jsou však účinné ve viditelném světelném spektru. Střed viditelného spektra má vlnovou délku přibližně 560 nm (pro sluneční světlo). Struktury fotonických krystalů mají obvykle poloviční nebo menší velikost, tedy <280 nm.
Plasmonické metamateriály využívají povrchové plazmony, což jsou pakety elektrického náboje, které kolektivně oscilují na povrchu kovů na optických frekvencích.
Frekvenčně selektivní povrchy (FSS) mohou vykazovat podvlnové charakteristiky a jsou známé různě jako umělé magnetické vodiče (AMC) nebo povrchy s vysokou impedancí (HIS). FSS vykazují induktivní a kapacitní charakteristiky, které přímo souvisejí s jejich subvlnovou strukturou.
Elektromagnetické metamateriály lze rozdělit do různých tříd, a to následovně:
Záporný index lomuEdit
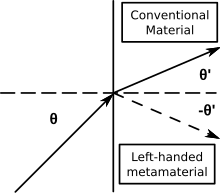
Metamateriály se záporným indexem (NIM) se vyznačují záporným indexem lomu. Mezi další termíny pro NIM patří „levotočivá média“, „média se záporným indexem lomu“ a „média se zpětnou vlnou“. NIM, u nichž záporný index lomu vyplývá ze současné záporné permitivity a záporné permeability, se také nazývají dvojité záporné metamateriály nebo dvojité záporné materiály (DNG).
Předpokládáme-li materiál dobře aproximovaný reálnou permitivitou a permeabilitou, platí vztah mezi permitivitou ϵ r {\displaystyle \epsilon _{r}}.

, permeabilita μ r {\displaystyle \mu _{r}}

a index lomu n je dán vztahem n = ± ϵ r μ r {\displaystyle \scriptstyle n=\pm {\sqrt {\epsilon _{\mathrm {r}. }\mu _{\mathrm {r} }}}}

. Všechny známé nemetamateriálové průhledné materiály (sklo, voda, …) mají kladné ϵ r {\displaystyle \epsilon _{r}}.

a μ r {\displaystyle \mu _{r}}.

. Podle konvence se pro n používá kladná odmocnina. Některé konstruované metamateriály však mají ϵ r {\displaystyle \epsilon _{r}}.

a μ r < 0 {\displaystyle \mu _{r}<0}.

. Protože součin ϵ r μ r {\displaystyle \epsilon _{r}\mu _{r}}.

je kladný, n je reálné. Za takových okolností je nutné vzít pro n zápornou odmocninu. Když oba ϵ r {\displaystyle \epsilon _{r}}.

a μ r {\displaystyle \mu _{r}}.

jsou kladné (záporné), vlny se pohybují směrem dopředu (dozadu). Elektromagnetické vlny se nemohou šířit v materiálech s ϵ r {\displaystyle \epsilon _{r}}.

a μ r {\displaystyle \mu _{r}}.

opačného znaménka, protože index lomu se stává imaginárním. Takové materiály jsou pro elektromagnetické záření neprůhledné a příkladem jsou plazmonické materiály, jako jsou kovy (zlato, stříbro, …).
Výše uvedené úvahy jsou zjednodušující pro skutečné materiály, které musí mít komplexní hodnotu ϵ r {\displaystyle \epsilon _{r}}.

a μ r {\displaystyle \mu _{r}}

. Reálné části obou ϵ r {\displaystyle \epsilon _{r}}.

a μ r {\displaystyle \mu _{r}}.

nemusí být záporné, aby pasivní materiál vykazoval záporný lom. Ve skutečnosti může záporný index lomu pro kruhově polarizované vlny vzniknout také v důsledku chirality. Metamateriály se záporným n mají řadu zajímavých vlastností:
- Snellův zákon (n1sinθ1 = n2sinθ2) stále popisuje lom, ale protože n2 je záporné, dopadající a lomené paprsky jsou na rozhraní materiálů s kladným a záporným indexem na stejné straně povrchové normály.
- Čerenkovovo záření ukazuje opačným směrem.
- Časově zprůměrovaný Poyntingův vektor je antiparalelní k fázové rychlosti. Aby se však vlny (energie) mohly šířit, musí být -µ spárováno s -ε, aby byla splněna závislost vlnového čísla na parametrech materiálu k c = ω μ ϵ {\displaystyle kc=\omega {\sqrt {\mu \epsilon }}}.
.
Záporný index lomu matematicky vyplývá z trojice vektorů E, H a k.
Pro rovinné vlny šířící se v elektromagnetických metamateriálech se elektrické pole, magnetické pole a vlnový vektor řídí levotočivým pravidlem, což je opak chování běžných optických materiálů.
Dosud pouze metamateriály vykazují záporný index lomu.
Jediné zápornéEdit
Jediné záporné (SNG) metamateriály mají buď zápornou relativní permitivitu (εr), nebo zápornou relativní permeabilitu (µr), ale ne obojí. V kombinaci s jiným, doplňkovým SNG se chovají jako metamateriály a společně působí jako DNG.
Epsilonově záporná média (ENG) vykazují záporné εr, zatímco µr je kladné. Tuto vlastnost vykazuje mnoho plazmat. Například ušlechtilé kovy, jako je zlato nebo stříbro, jsou ENG v infračerveném a viditelném spektru.
Mu negativní média (MNG) vykazují kladné εr a záporné µr. Tuto vlastnost vykazují gyrotropní nebo gyromagnetické materiály. Gyrotropní materiál je materiál, který byl změněn přítomností kvazistatického magnetického pole, což umožňuje magnetooptický efekt. Magnetooptický jev je jev, při kterém se elektromagnetická vlna šíří takovým prostředím. V takovém materiálu se mohou šířit levotočivé a pravotočivé eliptické polarizace různými rychlostmi. Při průchodu světla vrstvou magnetooptického materiálu se výsledek nazývá Faradayův jev: rovina polarizace se může otáčet, čímž vzniká Faradayův rotátor. Výsledky takového odrazu jsou známy jako magnetooptický Kerrův jev (nezaměňovat s nelineárním Kerrovým jevem). Dva gyrotropní materiály s obrácenými směry rotace obou hlavních polarizací se nazývají optické izomery.
Spojení desky z materiálu ENG a desky z materiálu MNG vedlo k vlastnostem, jako jsou rezonance, anomální tunelování, průhlednost a nulový odraz. Stejně jako materiály se záporným indexem jsou SNG vrozeně disperzní, takže jejich εr, µr a index lomu n, jsou funkcí frekvence.
HyperbolickéEdit
Hyperbolické metamateriály (HMM) se chovají jako kov pro určitou polarizaci nebo směr šíření světla a chovají se jako dielektrikum pro jiné díky záporné a kladné složce tenzoru permitivity, což dává extrémní anizotropii. Disperzní relace materiálu v prostoru vlnových vektorů tvoří hyperboloid, a proto se nazývá hyperbolický metamateriál. Extrémní anizotropie HMM vede ke směrovému šíření světla uvnitř i na povrchu. HMM vykazují různé potenciální aplikace, jako je snímání, zobrazování, řízení optických signálů, zesílené efekty plazmonové rezonance.
BandgapEdit
Elektromagnetické pásové metamateriály (EBG nebo EBM) řídí šíření světla. K tomu slouží buď fotonické krystaly (PC), nebo levotočivé materiály (LHM). PC mohou šíření světla zcela zakázat. Obě třídy mohou umožnit šíření světla v určitých navržených směrech a obě mohou být navrženy s pásmovými mezerami na požadovaných frekvencích. Velikost periody EBG je znatelným zlomkem vlnové délky, což vytváří konstruktivní a destruktivní interferenci.
PC se odlišují od struktur se subvlnovou délkou, jako jsou laditelné metamateriály, protože PC odvozují své vlastnosti od charakteristik pásmové mezery. PC jsou dimenzovány tak, aby odpovídaly vlnové délce světla, na rozdíl od jiných metamateriálů, které vystavují strukturu dílčí vlnové délky. Kromě toho PC fungují na principu difrakce světla. Naproti tomu metamateriál difrakci nevyužívá.
PC mají periodické inkluze, které brání šíření vln v důsledku destruktivní interference inkluzí z rozptylu. Fotonická pásmová vlastnost PC z nich dělá elektromagnetickou obdobu elektronických polovodičových krystalů.
EBG mají za cíl vytvářet vysoce kvalitní, nízkoztrátové, periodické, dielektrické struktury. EBG působí na fotony stejným způsobem jako polovodičové materiály na elektrony. Počítače jsou dokonalým materiálem s pásmovou mezerou, protože neumožňují šíření světla. Každá jednotka předepsané periodické struktury se chová jako jeden atom, i když mnohem větší velikosti.
EBG jsou navrženy tak, aby zabránily šíření přidělené šířky pásma frekvencí, pro určité úhly příchodu a polarizace. K výrobě speciálních vlastností EBG byly navrženy různé geometrie a struktury. V praxi je nemožné sestrojit bezchybné zařízení EBG.
EBG byly vyrobeny pro frekvence od několika gigahertzů (GHz) po několik terahertzů (THz), rádiové, mikrovlnné a středně infračervené frekvenční oblasti. Vývoj aplikací EBG zahrnuje přenosové vedení, dřevěné pilíře vyrobené ze čtvercových dielektrických tyčí a několik různých typů antén s nízkým ziskem.
Dvojitě kladné prostředíEdit
Dvojitě kladná prostředí (DPS) se v přírodě vyskytují, například přirozeně se vyskytující dielektrika. Permitivita i magnetická permeabilita jsou kladné a vlny se šíří v přímém směru. Byly vyrobeny umělé materiály, které kombinují vlastnosti DPS, ENG a MNG.
Bi-izotropní a bianizotropníEdit
Kategorizace metamateriálů na dvojitě negativní nebo dvojitě pozitivní obvykle předpokládá, že metamateriál má nezávislé elektrické a magnetické odezvy popsané ε a µ. V mnoha případech však elektrické pole způsobuje magnetickou polarizaci, zatímco magnetické pole indukuje elektrickou polarizaci, známou jako magnetoelektrická vazba. Taková média se označují jako bi-izotropní. Média, která vykazují magnetoelektrickou vazbu a která jsou anizotropní (což je případ mnoha metamateriálových struktur), se označují jako bi-anizotropní.
Čtyři materiálové parametry jsou vlastní magnetoelektrické vazbě bi-izotropních médií. Jsou to intenzita elektrického (E) a magnetického (H) pole a hustota elektrického (D) a magnetického (B) toku. Tyto parametry jsou ε, µ, κ a χ neboli permitivita, permeabilita, síla chirality a Tellegenův parametr. V tomto typu prostředí se materiálové parametry nemění se změnami podél otočeného souřadnicového systému měření. V tomto smyslu jsou invariantní neboli skalární.
Vlastní magnetoelektrické parametry, κ a χ, ovlivňují fázi vlny. Vlivem parametru chirality dochází k rozdělení indexu lomu. V izotropních prostředích to vede k šíření vln pouze tehdy, mají-li ε a µ stejné znaménko. V biziotropních médiích, kde se předpokládá, že χ je nulové a κ má nenulovou hodnotu, se objevují jiné výsledky. Může se objevit buď zpětná, nebo přímá vlna. Případně se mohou vyskytnout dvě dopředné nebo dvě zpětné vlny v závislosti na síle parametru chirality.
V obecném případě konstitutivní vztahy pro bi-anizotropní materiály zní D = ϵ E + ξ H , {\displaystyle \mathbf {D} =\epsilon \mathbf {E}. +\xi \mathbf {H} ,}

B = ζ E + μ H , {\displaystyle \mathbf {B} =\zeta \mathbf {E} +\mu \mathbf {H} ,}

kde ϵ {\displaystyle \epsilon }

a μ {\displaystyle \mu }

jsou tenzory permitivity a permeability, v tomto pořadí, zatímco ξ {\displaystyle \xi }

a ζ {\displaystyle \zeta }.

jsou dva magnetoelektrické tenzory. Je-li prostředí reciproční, jsou permitivita a permeabilita symetrické tenzory a ξ = – ζ T = – i κ T {\displaystyle \xi =-\zeta ^{T}=-i\kappa ^{T}}.

, kde κ {\displaystyle \kappa }

je chirální tenzor popisující chirální elektromagnetickou a reciprokou magnetoelektrickou odezvu. Chirální tenzor lze vyjádřit jako κ = 1 3 tr ( κ ) I + N + J {\displaystyle \kappa ={\tfrac {1}{3}}\operatorname {tr} (\kappa )I+N+J}

, kde tr ( κ ) {\displaystyle \operatorname {tr} (\kappa )}

je stopa κ {\displaystyle \kappa }

, I je identitní matice, N je symetrický tenzor bez stopy a J je antisymetrický tenzor. Takový rozklad nám umožňuje klasifikovat reciproční bianizotropní odezvu a můžeme identifikovat následující tři hlavní třídy: (i) chirální prostředí ( tr ( κ ) ≠ 0 , N ≠ 0 , J = 0 {\displaystyle \operatorname {tr} (\kappa )\neq 0,N\neq 0,J=0}

), ii) pseudochirální prostředí ( tr ( κ ) = 0 , N ≠ 0 , J = 0 {\displaystyle \operatorname {tr} ), ii) pseudochirální prostředí ( tr ( κ ) = 0 , N ≠ 0 , J = 0 {\displaystyle \operatorname {tr} ). (\kappa )=0,N\neq 0,J=0}

), iii) omega media ( tr ( κ ) = 0 , N = 0 , J ≠ 0 {\displaystyle \operatorname {tr} ), iii) omega media ( tr ( κ ) = 0 , N = 0 , J ≠ 0 {\displaystyle \operatorname {tr}) (\kappa )=0,N=0,J\neq 0}

).
ChiralEdit
Rukovitost metamateriálů je potenciálním zdrojem nejasností, protože v metamateriálové literatuře se vyskytují dvě protichůdná použití termínů levotočivý a pravotočivý. První označuje jednu ze dvou kruhově polarizovaných vln, které jsou šířícími se módy v chirálních prostředích. Druhý se týká trojice elektrického pole, magnetického pole a Poyntingova vektoru, které vznikají v médiích se záporným indexem lomu, která ve většině případů nejsou chirální.
Obecně je chirální a/nebo bianizotropní elektromagnetická odezva důsledkem 3D geometrické chirality: 3D-chirální metamateriály jsou tvořeny vložením 3D-chirálních struktur do hostitelského média a vykazují polarizační efekty související s chiralitou, jako je optická aktivita a kruhový dichroismus. Existuje také pojem 2D chiralita a o rovinném objektu se říká, že je chirální, pokud nemůže být superponován na svůj zrcadlový obraz, pokud není zvednut z roviny. Bylo pozorováno, že 2D-chirální metamateriály, které jsou anizotropní a ztrátové, vykazují směrově asymetrický přenos (odraz, absorpci) kruhově polarizovaných vln v důsledku kruhového konverzního dichroismu. Na druhé straně může bianizotropní odezva vznikat z geometrických achirálních struktur, které nemají ani 2D, ani 3D vnitřní chiralitu. Švestka a jeho kolegové zkoumali magnetoelektrickou vazbu v důsledku vnější chirality, kdy se uspořádání (achirální) struktury spolu s vektorem vlny záření liší od jejího zrcadlového obrazu, a pozorovali velkou, laditelnou lineární optickou aktivitu, nelineární optickou aktivitu, zrcadlovou optickou aktivitu a dichroismus kruhové konverze. Rizza a spol. navrhli 1D chirální metamateriály, kde efektivní chirální tenzor není mizivý, pokud je systém geometricky jednorozměrně chirální (zrcadlový obraz celé struktury na něj nelze superponovat pomocí translace bez rotace).
3D-chirální metamateriály jsou konstruovány z chirálních materiálů nebo rezonátorů, v nichž je efektivní parametr chirality κ {\displaystyle \kappa }.

je nenulový. Vlastnosti šíření vln v takových chirálních metamateriálech ukazují, že záporný lom lze realizovat v metamateriálech se silnou chiralitou a kladným ϵ r {\displaystyle \epsilon _{r}}.

a μ r {\displaystyle \mu _{r}}.

. Je to proto, že index lomu n {\displaystyle n}

má odlišné hodnoty pro levou a pravou kruhově polarizovanou vlnu, dané vztahem
n = ± ϵ r μ r ± κ {\displaystyle n=\pm {\sqrt {\epsilon _{r}\mu _{r}}}pm \kappa }

Je vidět, že záporný index nastane pro jednu polarizaci, pokud κ {\displaystyle \kappa }

> ϵ r μ r {\displaystyle {\sqrt {\epsilon _{r}\mu _{r}}}}

. V tomto případě není nutné, aby buď ϵ r {\displaystyle \epsilon _{r}}, nebo oba ϵ r {\displaystyle \epsilon _{r}}.

a μ r {\displaystyle \mu _{r}}.

být pro zpětné šíření vlny záporné. Záporný index lomu způsobený chiralitou poprvé současně a nezávisle na sobě pozorovali Plum et al. a Zhang et al. v roce 2009.
FSS basedEdit
Frekvenčně selektivní metamateriály na bázi povrchu blokují signály v jednom vlnovém pásmu a propouštějí signály v jiném vlnovém pásmu. Staly se alternativou k metamateriálům s pevnou frekvencí. Umožňují volitelné změny frekvencí v jednom médiu namísto omezujících limitů pevné frekvenční odezvy
.
