V učebnici zobecněných lineárních modelů jsme se seznámili s různými GLM, jako je lineární regrese, logistická regrese atd.. V tomto tutoriálu ze série TechVidvan’s R tutorial se budeme podrobně zabývat lineární regresí v R. Dozvíme se, co je lineární regrese v R a jak ji implementovat v R. Podíváme se na metodu odhadu nejmenších čtverců a také se naučíme, jak ověřit přesnost modelu.

Takže, bez dalších řečí, začneme!

Lineární regrese v R

Lineární regrese v R je metoda používaná k předpovědi hodnoty proměnné pomocí hodnoty (hodnot) jedné nebo více vstupních predikčních proměnných. Cílem lineární regrese je vytvořit lineární vztah mezi požadovanou výstupní proměnnou a vstupními prediktory.

Modelovat spojitou proměnnou Y jako funkci jedné nebo více vstupních predikčních proměnných Xi tak, aby tato funkce mohla být použita k předpovědi hodnoty Y, když jsou známy pouze hodnoty Xi. Obecný tvar takového lineárního vztahu je:

Y=?0+?1 X

Tady ?0 je intercept
a ?1 je sklon.

Typy lineární regrese v R

Existují dva typy lineární regrese v R:

• Jednoduchá lineární regrese
• Vícenásobná lineární regrese

Podívejme se na ně postupně.

Jednoduchá lineární regrese v R

Jednoduchá lineární regrese je zaměřena na hledání lineárního vztahu mezi dvěma spojitými proměnnými. Je důležité si uvědomit, že jde o vztah statistické povahy, nikoli deterministický.

Deterministický vztah je takový, kdy hodnotu jedné proměnné lze přesně zjistit pomocí hodnoty druhé proměnné. Příkladem deterministického vztahu je vztah mezi kilometry a mílemi. Pomocí hodnoty kilometrů můžeme přesně zjistit vzdálenost v mílích. Statistický vztah není přesný a vždy obsahuje chybu předpovědi. Například při dostatečném množství dat můžeme najít vztah mezi výškou a hmotností člověka, ale vždy bude existovat určitá chyba a budou existovat výjimečné případy.

Smyslem jednoduché lineární regrese je najít přímku, která nejlépe odpovídá daným hodnotám obou proměnných. Tato přímka nám pak může pomoci najít hodnoty závislé proměnné, pokud chybějí.

Nastudujme si to na příkladu. Máme soubor dat, který se skládá z výšek a hmotností 500 osob. Naším cílem je zde sestavit lineární regresní model, který formuluje vztah mezi výškou a hmotností tak, že když modelu zadáme jako vstup výšku(Y), může nám na oplátku dát hmotnost(X) s minimálním rozpětím nebo chybou.

Y=b0+b1X

Hodnoty b0 a b1 by měly být zvoleny tak, aby minimalizovaly rozpětí chyby. Metriku chyby můžeme použít k měření přesnosti modelu.

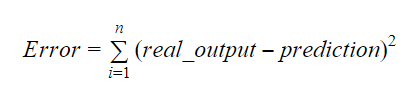
Sklon nebo koeficient můžeme vypočítat jako: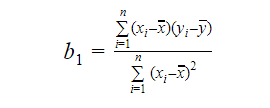

Hodnota b1 nám dává představu o charakteru vztahu mezi závislou a nezávislou proměnnou.

• Pokud je b1 > 0, pak mají proměnné kladný vztah, tj. zvýšení x bude mít za následek zvýšení y.
• Pokud b1 < 0, pak proměnné mají záporný vztah, tj. zvýšení x bude mít za následek snížení y.

Hodnotu b0 neboli interceptu lze vypočítat takto: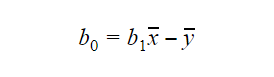
Hodnota b0 může také poskytnout mnoho informací o modelu a naopak.

Pokud model neobsahuje x=0, pak předpověď bez b1 nemá smysl. Aby model v libovolném bodě obsahoval pouze b0 a nikoliv b1, musí být hodnota x v tomto bodě 0. V případech, jako je výška, x nemůže být 0 a výška člověka nemůže být 0. Proto je takový model pouze s b0 nesmyslný.

Pokud člen b0 chybí, pak model prochází počátkem, což znamená, že předpověď a regresní koeficient(sklon) budou zkreslené.

Vícenásobná lineární regrese v R

Vícená lineární regrese je rozšíření jednoduché lineární regrese. Ve vícenásobné lineární regresi se snažíme vytvořit lineární model, který dokáže předpovědět hodnotu cílové proměnné pomocí hodnot více predikčních proměnných. Obecný tvar takové funkce je následující:

Y=b0+b1X1+b2X2+…+bnXn

Ohodnocení přesnosti modelu

Existují různé metody hodnocení kvality a přesnosti modelu. Podívejme se postupně na některé z těchto metod.

R-Squared

Skutečnou informací v datech je rozptyl v nich vyjádřený. R-squared nám říká, jaký podíl variability cílové proměnné (y) vysvětluje model. Míru R-squared modelu můžeme zjistit pomocí následujícího vzorce: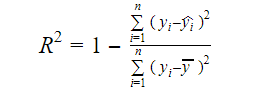

Kde,

• yi je fitovaná hodnota y pro pozorování i
• y je střední hodnota Y.

Nižší hodnota R-squared znamená nižší přesnost modelu. Míra R-squared však nemusí být nutně konečným rozhodujícím faktorem.

Adjusted R-Squared

S rostoucím počtem proměnných v modelu roste i hodnota R-squared. To také způsobuje chyby ve variabilitě vysvětlené nově přidanými proměnnými. Proto upravíme vzorec pro R square pro více proměnných.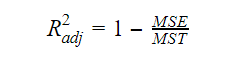
Zde MSE znamená Mean Standard Error, což je:

A MST znamená Mean Standard Total, což je dáno: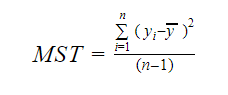

Kde n je počet pozorování a q je počet koeficientů.

Vztah mezi R-kvadrátem a upraveným R-kvadrátem je: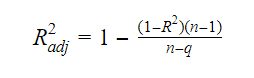

Standardní chyba a F-statistika

Standardní chyba i F-statistika jsou mírou kvality shody modelu. Vzorce pro standardní chybu a F-statistiku jsou následující:

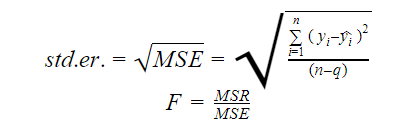
Kde MSR znamená Mean Square Regression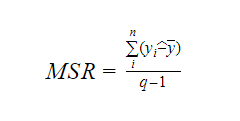

AIC a BIC

Akaikeho informační kritérium a Bayesovo informační kritérium jsou míry kvality shody statistických modelů. Lze je také použít jako kritéria pro výběr modelu.

AIC=(-2)*ln(L)+2*k
BIC=(-2)*ln(L)+k*ln(n)

Kde,

• L je pravděpodobnostní funkce,
• k je počet parametrů modelu,
• n je velikost vzorku.

funkce lm v R

Funkce lm() v R se hodí pro lineární modely. Může provádět regresi a analýzu rozptylu a kovariance. Syntaxe funkce lm je následující:

lm(formula, data, subset, weights, na.action,method = "qr", model = TRUE, x = FALSE, y = FALSE, qr = TRUE,singular.ok = TRUE, offset, …)

Kde,

• vzorec je objekt třídy „vzorec“ a je symbolickou reprezentací modelu, který se má fitovat,
• data je datový rámec nebo seznam, který obsahuje proměnné ve vzorci(data je nepovinný argument. Pokud chybí, funkce přebírá proměnné z prostředí),
• subset je nepovinný vektor obsahující podmnožinu pozorování, která mají být použita v procesu fitování,
• weights je nepovinný vektor, který určuje váhy, které mají být použity v procesu fitování,
• na.action je funkce, která ukazuje, co se má stát, když se v datech vyskytnou NA,
• method označuje metodu fitování modelu,
• model, x, y a qr jsou logické znaky, které řídí, zda mají být příslušné hodnoty vráceny s výstupem, nebo ne. Tyto hodnoty jsou:
• model: rámec modelu
• x: matice modelu
• y: odezva
• qr: rozklad qr
• singular.ok je logická, která řídí, zda jsou singulární uložení povolena nebo ne,
• offset je předem známý prediktor, který má být v modelu použit,
• . . . jsou další argumenty, které se předávají regresním funkcím nižší úrovně.

Praktický příklad lineární regrese v R

Prozatím dost teorie. Podívejme se, jak to všechno implementovat. Budeme fitovat lineární model pomocí lineární regrese v R s pomocí funkce lm(). Následně také zkontrolujeme kvalitu shody modelu. Použijeme datovou sadu cars, která je ve výchozím nastavení k dispozici v základním balíčku R.

1. Začneme grafickou analýzou datové sady, abychom se s ní lépe seznámili. Za tímto účelem nakreslíme graf rozptylu a ověříme, co nám o datech vypovídá.

Pomocí funkce scatter.smooth() vytvoříme graf rozptylu pro datovou sadu.

scatter.smooth(x=cars$speed,y=cars$dist,main="TechVidvan Dist ~ Speed")

Výstup

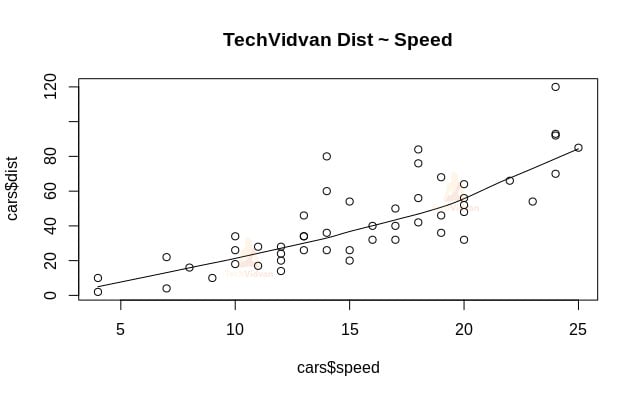
Karta rozptylu nám ukazuje pozitivní korelaci mezi vzdáleností a rychlostí. Naznačuje lineárně rostoucí vztah mezi oběma proměnnými. Díky tomu jsou data vhodná pro lineární regresi, protože lineární vztah je základním předpokladem pro dosazení lineárního modelu na data.

2. Nyní, když jsme si ověřili, že lineární regrese je pro data vhodná, můžeme na ně pomocí funkce lm() dosadit lineární model.

Linear_model <- lm(dist~speed,data=cars)print(Linear_model)

Výstup

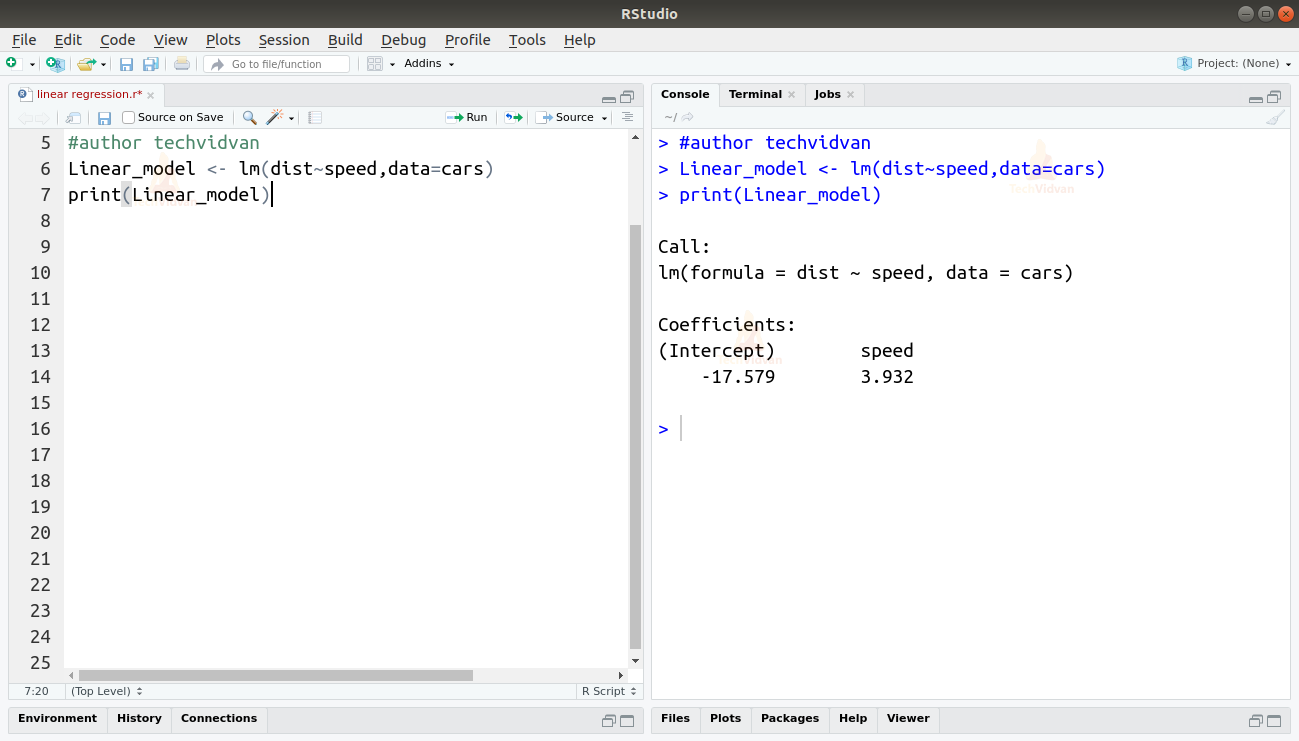
Výstup funkce lm() nám ukazuje intercept a koeficient rychlosti. Definujeme tedy lineární vztah mezi vzdáleností a rychlostí takto:

Vzdálenost=Intercept+koeficient*rychlost

Vzdálenost=-17,579+3,932*rychlost

3. Nyní, když jsme dosadili model, zkontrolujme kvalitu neboli správnost dosazení. Začněme kontrolou souhrnu lineárního modelu pomocí funkce summary().

summary(Linear_model)

Výstup

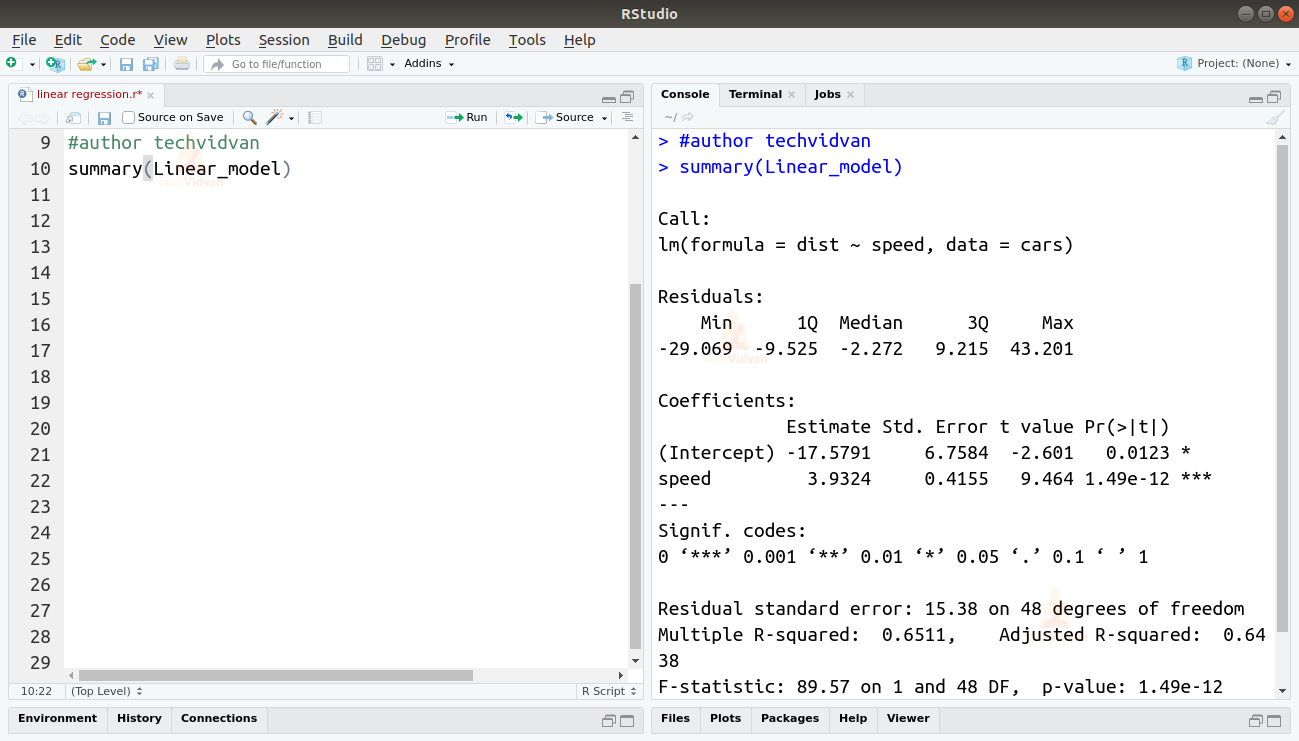
Funkce summary() nám poskytuje několik důležitých ukazatelů, které nám pomohou diagnostikovat vhodnost modelu. Hodnota p je důležitým měřítkem dobré shody modelu. O modelu se říká, že není vhodný, pokud je p-hodnota větší než předem stanovená hladina statistické významnosti, která je v ideálním případě 0,05.

Souhrn nám také poskytuje t-hodnotu. Čím větší je t-hodnota, tím lépe model vyhovuje.
Můžeme také zjistit AIC a BIC pomocí funkcí AIC() a BIC().

AIC(Linear_model)BIC(Linear_model)

Výstup

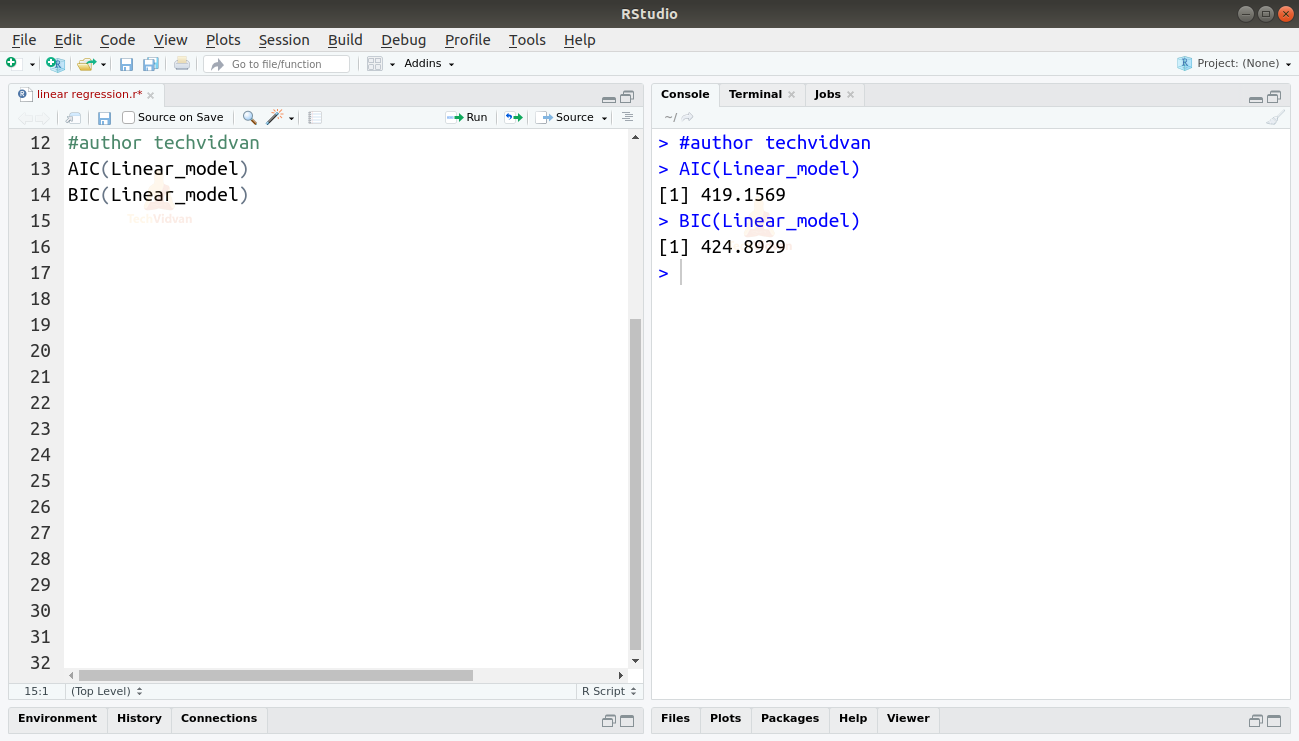
Nejvýhodnější je model, jehož výsledkem je nejnižší skóre AIC a BIC.

Shrnutí

V této kapitole výukového seriálu TechVidvan v R jsme se seznámili s lineární regresí. Seznámili jsme se s jednoduchou lineární regresí a vícenásobnou lineární regresí. Dále jsme studovali různé míry pro posouzení kvality nebo přesnosti modelu, jako je R2, upravené R2, standardní chyba, F-statistika, AIC a BIC. Poté jsme se naučili implementovat lineární regresi v jazyce R. Následně jsme zkontrolovali kvalitu přizpůsobení modelu v jazyce R.

Podělte se o své hodnocení na Googlu, pokud se vám výukový program Lineární regrese líbil.