Úvod

Model latentní sémantické analýzy je teorií, jak se lze naučit významové
reprezentace na základě setkání s velkými vzorky jazyka bez explicitních pokynů, jak je strukturován.
Problém, který máme v ruce, není pod dohledem, tj. nemáme korpusu přiřazeny pevné značky nebo kategorie.

Aby bylo možné z dokumentů extrahovat vzory a porozumět jim, LSA se ze své podstaty řídí určitými předpoklady:
1) Význam věty nebo dokumentu je souhrnem významů všech slov, která se v něm vyskytují. Celkově je význam určitého slova průměrem všech dokumentů, v nichž se vyskytuje.
2) LSA předpokládá, že sémantické asociace mezi slovy nejsou přítomny explicitně, ale pouze latentně ve velkém vzorku jazyka.

Matematický pohled

Latentní sémantická analýza (LSA) se skládá z určitých matematických operací pro získání vhledu do dokumentu. Tento algoritmus tvoří základ tematického modelování. Základní myšlenkou je vzít matici toho, co máme – dokumenty a termíny – a rozložit ji na samostatnou matici dokument-téma a matici téma-termín.

Prvním krokem je vygenerování naší matice dokument-termín pomocí vektorizátoru Tf-IDF. Lze ji také zkonstruovat pomocí modelu Bag-of-Words, ale výsledky jsou řídké a nepřinášejí žádný význam pro věc.
Dáme-li m dokumentů a n-slov v našem slovníku, můžeme zkonstruovat matici
m × n A, v níž každý řádek představuje dokument a každý sloupec slovo.

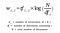
Intuitivně má termín velkou váhu, pokud se v dokumentu vyskytuje často, ale v korpusu málo často.
Pomocí této transformační metody (tf-IDF) vytvoříme matici dokumentů-termínů A, kterou vektorizujeme náš korpus. ( Tak, aby to náš další model dokázal zpracovat nebo vyhodnotit, protože zatím nepracujeme s řetězci!).
Je tu však jemná nevýhoda, pozorováním A nemůžeme nic odvodit, protože je to zašuměná a řídká matice. ( Někdy je příliš velká i na to, aby se dala vypočítat pro další procesy).

Protože je modelování témat ze své podstaty nesupervisovaný algoritmus, musíme latentní témata předem určit. Jedná se o obdobu shlukování K-Means tak, že předem určíme počet shluků.

V tomto případě provedeme Low-Rank aproximaci pomocí techniky redukce dimenzionality s využitím zkráceného rozkladu singulární hodnoty (SVD).
Rozklad singulární hodnoty je technika v lineární algebře, která faktorizuje libovolnou matici M na součin 3 samostatných matic:

Truncated SVD redukuje dimenzionalitu výběrem pouze t největších singulárních hodnot a ponecháním pouze prvních t sloupců U a V. V tomto případě je t hyperparametr, který můžeme zvolit a upravit tak, aby odrážel počet témat, která chceme najít.

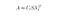
Poznámka: Zkrácená SVD provádí redukci dimenzionality a ne SVD!

S těmito vektory dokumentů a vektory termínů můžeme nyní snadno použít k vyhodnocení míry, jako je kosinová podobnost:

• podobnost různých dokumentů
• podobnost různých slov
• podobnost termínů (neboli „dotazů“) a dokumentů (což se stává užitečným při vyhledávání informací, když chceme získat pasáže nejrelevantnější pro náš vyhledávací dotaz).

Závěrečné poznámky

Tento algoritmus se používá především v různých úlohách založených na NLP a je základem robustnějších metod, jako je pravděpodobnostní LSA a Latentní Dirichletova alokace (LDA).

Kushal Vala, Junior Data Scientist ve společnosti Datametica Solutions Pvt Ltd

.