V tomto článku vás seznámím se základy udržování kvality.

Jedná se o zajištění kvality, kontrolu kvality a metrologii. Zajišťování kvality používáme k získání jistoty, že požadavky na kvalitu budou splněny. Kontrolu kvality používáme k ověření, že požadavky byly splněny. Jedná se o jemný rozdíl a v praxi se tyto pojmy někdy používají zaměnitelně. Metrologie je věda o měření. Je to způsob, jak zajistit, abychom mohli s jistotou porovnávat výsledky měření provedených po celém světě.

Tyto zásady se mohou týkat výrobků nebo služby, ale já se zaměřím na výrobu a na to, jak spolu tyto tři základní pojmy v této souvislosti souvisejí. Vyhnul jsem se proto podrobnostem konkrétních metod a nezabývám se žádnou matematikou. Tu si nechám na pozdější článek.

Počátky měření

Egypťané používali etalony měření s pravidelnou kalibrací, aby zajistili, že kameny budou do sebe zapadat při jejich velkých stavebních projektech. Moderní systémy kvality však skutečně vznikly až během průmyslové revoluce. Do té doby vyráběli mechanické zboží řemeslníci, kteří každou součástku jednotlivě upravovali tak, aby zapadla do sestavy. To znamenalo, že každý stroj a každá jeho součástka byly jedinečné. Pokud bylo třeba díl vyměnit, musel řemeslník namontovat nový díl.

Koncem 18. století začali francouzští výrobci zbraní vyrábět muškety se standardními díly. To znamenalo, že armáda mohla mít u sebe náhradní díly a rychle je vyměnit za rozbité. Tyto vyměnitelné díly se stále montovaly do sestavy, ale místo aby se každý díl montoval do jednotlivé zbraně, montoval se do hlavního dílu .

O několik let později začali tuto metodu používat američtí výrobci zbraní, ale přizpůsobili ji svým neškoleným dělníkům. Vypilovali měřidla, která se hodila k hlavnímu dílu, dělníci nastavovali přípravky a výrobní stroje pomocí měřidel a také používali měřidla ke kontrole dílů. Díky tomu mohla řada strojů, z nichž každý prováděl jednu operaci s nekvalifikovanou obsluhou, vyrábět přesné díly. Tyto díly pak bylo možné rychle sestavit do složitých strojů.

Základy moderní výroby tak byly položeny více než 100 let předtím, než Ford tyto myšlenky uplatnil na pohyblivé výrobní lince.

Kalibrace, skutečná hodnota a chyba měření

Systém hlavních dílů, měřidel a strojů na jedno použití fungoval, když se celý výrobek vyráběl v jedné továrně. Moderní globální dodavatelské řetězce potřebují jiný systém.

Místo fyzického hlavního dílu máme výkres nebo digitální model CAD. Specifikované tolerance zajišťují, že díly do sebe zapadnou a budou fungovat tak, jak mají. Místo toho, aby každý výrobce přicházel k jednomu vzorovému dílu a nastavoval svá měřidla, nechává si kalibrovat své měřicí přístroje. Tyto přístroje se pak používají k nastavení výrobních strojů a ke kontrole vyrobených dílů.

Na tomto procesu kalibrace závisí veškerá kvalita.

Nejdůležitějším pojmem, který je třeba pochopit, je, že všechna měření mají nejistotu. Kdybych vás požádal, abyste odhadli výšku tohoto textu, mohli byste říci: “ je to asi 4 mm“ . Použití slova „asi“ znamená, že ve vašem odhadu je určitá nejistota.

Ve skutečnosti nikdy nemůžeme znát přesnou skutečnou hodnotu čehokoli, všechna měření jsou vlastně odhady a mají určitou nejistotu. Rozdíl mezi výsledkem měření a skutečnou hodnotou je chyba měření . Protože nemůžeme znát skutečnou hodnotu, nemůžeme znát ani chybu: jedná se o nepoznatelné veličiny.

Vše, co můžeme o světě kolem nás kvantifikovat, jsou výsledky měření a ty mají vždy určitou nejistotu, i když je tato nejistota velmi malá.

Přesnost a nejistota. (Obrázek s laskavým svolením autora.)

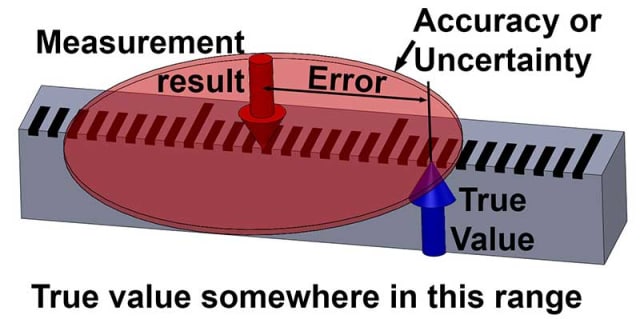
Pokud byste odhadli výšku tohoto textu jako ‚ asi 4 mm, plus minus 1 mm‘, pak jste nyní přiřadili určité hranice nejistoty. Stále si však nemůžete být stoprocentně jisti, že je to pravda.

Můžete mít určitou míru jistoty, řekněme 95 procent, že je to pravda. Kdybyste tyto meze zvýšili, řekněme plus minus na 2 mm , pak by se vaše jistota zvýšila, třeba na 99 procent. Nejistota tedy udává nějaké meze, v jejichž rámci máme určitou úroveň jistoty, že pravdivá hodnota leží.

OK, hodina filozofie skončila!

V některém z příštích příspěvků tyto myšlenky rozvedu a vysvětlím, jak lze nejistotu pro určitou úroveň spolehlivosti vypočítat.

Nejistota a kvalita

Jakmile určíme nejistotu (nebo „přesnost“) měření, můžeme ji použít při rozhodování, zda díl odpovídá stanovené toleranci. Řekněme například, že u dílu je specifikováno, že má mít 100 mm +/- 1 mm. Změříme ji a dostaneme výsledek 100,87 mm.

Je díl v souladu se specifikací?

Jednoduchá odpověď zní: „Nevíme, možná je, ale možná došlo k chybě v našem měření a ve skutečnosti je díl větší než 101 mm. Možná došlo k ještě větší chybě a díl je ve skutečnosti menší než 99 mm!“.

Pokud nevíme, jaká je nejistota měření, netušíme, nakolik si můžeme být jisti, že díl odpovídá specifikaci. Předpokládejme, že nejistota měření byla dána tak, že výsledek měření je 100,87 mm +/- 0,1 mm při 95% spolehlivosti. Nyní můžeme s jistotou lepší než 95 procent říci, že díl je ve specifikaci.

Pochopení a kvantifikace nejistoty měření je tedy pro udržení kvality rozhodující.

Nyní se zamysleme nad kalibrací a souvisejícím konceptem návaznosti. Jedná se o základní aspekt nejistoty. Kalibrace je porovnání s referencí a nejistota tohoto porovnání musí být vždy zahrnuta, a to z důvodů vysvětlených níže.

Navazující měření je takové, které má nepřerušený řetězec kalibrací jdoucí až k primárnímu etalonu. V případě měření délky je primárním etalonem definice metru; vzdálenost, kterou urazí světlo ve vakuu za 1/299 792 458 sekundy, jak ji realizuje Mezinárodní úřad pro míry a váhy (BIPM) v Paříži.

Měření je sledovatelné, pokud existuje nepřerušený řetězec kalibrací zpět k primárnímu etalonu. (Obrázek s laskavým svolením autora.)

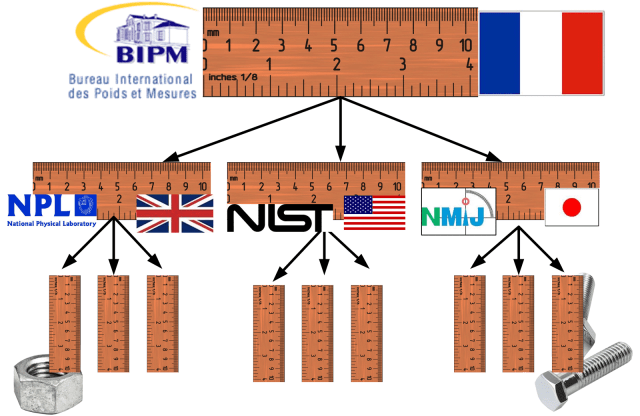
Od 30. let 20. století je palec definován jako 25,4 mm, a proto je také navázán na stejný etalon metru. Všechna měření musí být navázána na stejný etalon, aby bylo zajištěno, že díly vyrobené v různých zemích k sobě budou pasovat.

Nejistota a chyba

Nejistota měření vzniká z různých zdrojů. Některé z nich povedou k soustavné chybě nebo zkreslení výsledku.

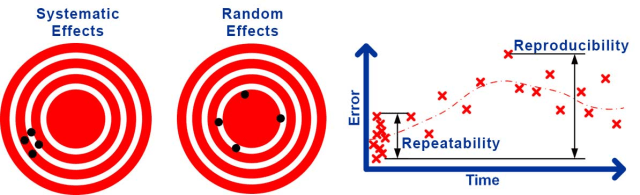
Například neznámá chyba přítomná při kalibraci přístroje povede ke konstantní chybě při každém jeho použití. Tento typ vlivu je znám jako systematická nejistota vedoucí k systematické chybě . Jiné zdroje povedou k chybám, které se náhodně mění při každém měření.

Například turbulence ve vzduchu může způsobit malé, náhodně se měnící poruchy laserových měření, mechanická vůle a seřízení může způsobit náhodně se měnící chybu mechanických měření. Tento typ vlivu je znám jako náhodná nejistota vedoucí k náhodné chybě .

Je obvyklé dělit náhodnou nejistotu na opakovatelnost , náhodnou nejistotu výsledků za stejných podmínek, a reprodukovatelnost , náhodnou nejistotu za změněných podmínek.

Podmínky samozřejmě nikdy nemohou být přesně stejné nebo zcela odlišné, takže toto rozlišení je poněkud vágní. Typy podmínek, které mohou být změněny, jsou provádění měření v jiném čase, s jinou obsluhou, jiným přístrojem, s použitím jiné kalibrace a v jiném prostředí.

Systematické vs. náhodné efekty. (Obrázek se svolením autora.)

Existují dvě široce používané metody kvantifikace nejistoty měření. Kalibrační laboratoře a vědecké instituce obvykle provádějí vyhodnocení nejistoty podle Příručky pro vyjádření nejistoty měření (GUM) .

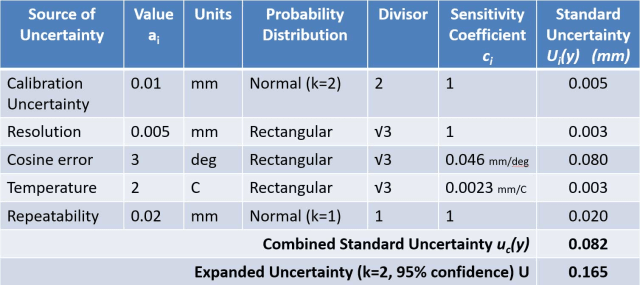
Metoda GUM zahrnuje nejprve zvážení všech vlivů, které mohou ovlivnit výsledek měření. Poté je třeba stanovit matematický model udávající výsledek měření jako funkci těchto ovlivňujících veličin. Zvážením nejistoty každé vstupní veličiny a použitím ‚ zákona šíření nejistoty ‚ lze vypočítat odhad kombinované nejistoty měření.

Přístup GUM se někdy označuje jako přístup zdola nahoru , protože začíná úvahou o každém jednotlivém vlivu. Každý vliv je obvykle uveden v tabulce zvané rozpočet nejistoty, která se používá k výpočtu kombinované nejistoty.

Příklad rozpočtu nejistoty. (Obrázek s laskavým svolením autora.)

Průmyslové měřicí procesy se obvykle vyhodnocují pomocí přístupu analýzy měřicích systémů (MSA), jak je doporučeno v rámci metodiky Six-Sigma, a obvykle podle pokynů referenční příručky MSA skupiny Automotive Industry Action Group (AIAG) .

MSA zahrnuje provádění studií měřidel, při nichž se opakovaná měření porovnávají s referencí za různých podmínek, aby se určila odchylka, opakovatelnost a někdy i reprodukovatelnost.

Studie měřidla typu 1 je rychlá kontrola, která se obvykle provádí pro počáteční pochopení variability měřidla. Zahrnuje měření jednoho kalibrovaného referenčního dílu jedním operátorem 25krát nebo vícekrát a poté se zvažuje variabilita a bias výsledků. Tento typ testu se mimo MSA často nazývá studie opakovatelnosti.

Studie opakovatelnosti a reprodukovatelnosti měřidla (Gage R&R) se používá k podrobnějšímu pochopení procesu měření. Obvykle se měří 10 dílů, každý dvakrát, a to nejméně třemi různými operátory. Pomocí statistické techniky zvané ANOVA se pak určí, jaká část odchylek je způsobena přístrojem („měřidlem“) a jaká část je způsobena obsluhou. Změna operátora a následné změny v čase a prostředí se přitom považují za úplné zobrazení podmínek reprodukovatelnosti.

MSA se někdy označuje jako metoda shora dolů, protože do značné míry považuje proces měření za černou skříňku a experimentálně určuje systematické a náhodné nejistoty. Dva důležité pojmy v MSA jsou přesnost , používaná jako ekvivalent nejistoty, a preciznost , používaná jako ekvivalent náhodné nejistoty.

Výhodou vyhodnocení nejistoty je, že je schopno zohlednit všechny zdroje nejistoty, a pokud je provedeno správně, poskytuje nejpřesnější odhad nejistoty. Mezi problémy tohoto přístupu patří skutečnost, že vyžaduje metrologa schopného vytvořit matematický model, a riziko lidské chyby vedoucí k opomenutí nebo nesprávnému odhadu významných vlivů.

Metoda GUM je také platná pouze pro jednotlivé měření, které bylo provedeno se známými hodnotami všech použitých korekcí. Proto je obtížné správně použít vyhodnocení nejistoty k předpovědi nejistoty průmyslového procesu měření.

MSA lze použít mnohem snadněji a je určena k předpovědi přesnosti průmyslového procesu měření. Problémem tohoto přístupu je, že jsou ignorovány určité systematické vlivy a podmínky reprodukovatelnosti nemusí být plně zastoupeny, což vede k podhodnocení nejistoty.

Příkladem opomenutí systematických vlivů je to, že při určování odchylky se provádí srovnání s referencí, která se považuje za skutečnou hodnotu – ve skutečnosti má reference také nejistotu, která by měla být zahrnuta. Tato metoda se opírá o to, že všechny podmínky reprodukovatelnosti se mění tak, aby jejich vliv byl patrný na variabilitě výsledků při opakovaných měřeních. Je pravděpodobné, že způsob, jakým se tyto podmínky mění, nebude plně odrážet odchylky pozorované během skutečného procesu měření.

Měření a zajištění jakosti

Dosud jsem se zaměřil na kontrolu jakosti, tj. na to, jak lze měřením prokázat, že díly po výrobě odpovídají specifikacím. Nyní se krátce věnujme zajištění kvality, tedy způsobu, jakým zajistíme, aby proces vůbec produkoval dobré díly.

Tímto aspektem kvality se z velké části zabývá statistické řízení procesu (SPC) . Proces lze vyhodnotit tak, že se vyrobí několik dílů a změří se, aby se zjistila variabilita a odchylka výrobního procesu. Namísto přímého udání těchto výsledků je obvyklé vydělit toleranci dílu přesností procesu a získat tak způsobilost obráběcího stroje ( C P ) nebo přesnost procesu a získat tak způsobilost procesu ( C PK ).

SPC je v mnoha ohledech ekvivalentní MSA. Využívá přístup shora dolů k pochopení náhodných a systematických vlivů. Místo vyhodnocování měření se však používá k vyhodnocování výstupů procesu. Obecně má stejné výhody a nevýhody jako MSA, a pokud jsou tyto problémy, lze použít přístup hodnocení nejistot zdola nahoru.

Zpočátku se může zdát, že mezi MSA a SPC existují zásadní rozdíly vzhledem k velmi odlišné terminologii v rámci SPC. Nicméně variabilita běžných příčin (nebo variabilita náhodných příčin ve starší literatuře) je ekvivalentem přesnosti; krátkodobá variabilita je ekvivalentem opakovatelnosti; dlouhodobá variabilita je ekvivalentem reprodukovatelnosti; a variabilita zvláštních příčin (nebo variabilita přiřaditelných příčin ve starší literatuře) je ekvivalentem vychýlení.

SPC také klade mnohem větší důraz na zajištění toho, aby byl proces pod „statistickou kontrolou“. V širším smyslu to znamená, že účinky jsou náhodné a normálně rozdělené s korekcí jakýchkoli významných systematických vlivů. To je silná stránka SPC, která je někdy přehlížena jak při hodnocení nejistoty, tak při MSA.

Hlavním nástrojem používaným v SPC ke kontrole „kontrolovaného“ procesu je regulační diagram . To umožňuje jednoduché grafické zobrazení procesu, při kterém lze snadno zjistit, kdy proces driftuje nebo produkuje chyby, které nelze vysvětlit běžnými náhodnými odchylkami. Například pokud několik bodů roste nebo klesá, znamená to, že proces driftuje.

Příklad regulačního diagramu. (Obrázek se svolením autora.)

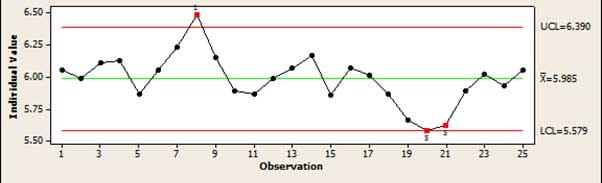
V tomto článku jsem se snažil podat široký přehled rozsáhlého a složitého tématu. Představil jsem základní principy udržování kvality, aniž bych se pouštěl do matematiky potřebné k aplikaci těchto metod.

Zůstaňte naladěni na další články na tato témata.

Dvacetiletá inženýrská kariéra Dr. Jodyho Muelanera začala v oblasti konstrukce strojů, kde pracoval na všem možném od lékařských přístrojů až po pily. Od roku 2007 se na univerzitě v Bathu věnuje vývoji nové metrologie a úzce spolupracuje s předními leteckými společnostmi. Tento výzkum se v současné době zaměřuje na modelování nejistoty výrobních systémů a spojuje prvky SPC, MSA a metrologie s novými numerickými metodami. Zajímá se také o design jízdních kol. Další informace naleznete na jeho webových stránkách.