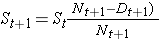We willen vaak nagaan of er verschillen zijn in overleving (of cumulatieve incidentie van voorvallen) tussen verschillende groepen deelnemers. In een klinisch onderzoek met een overlevingsuitkomst willen we bijvoorbeeld de overleving vergelijken tussen deelnemers die een nieuw geneesmiddel krijgen en deelnemers die een placebo (of standaardtherapie) krijgen. In een observationele studie kunnen we geïnteresseerd zijn in een vergelijking van de overleving tussen mannen en vrouwen, of tussen deelnemers met en zonder een bepaalde risicofactor (bv. hypertensie of diabetes). Er zijn verschillende tests beschikbaar om de overleving tussen onafhankelijke groepen te vergelijken.
De Log Rank Test
De log rank test is een populaire test om de nulhypothese te testen van geen verschil in overleving tussen twee of meer onafhankelijke groepen. De test vergelijkt de gehele overlevingservaring tussen groepen en kan worden opgevat als een test of de overlevingskrommen identiek (overlappend) zijn of niet. De overlevingskrommen worden voor elke groep afzonderlijk geschat met behulp van de Kaplan-Meier-methode en statistisch vergeleken met behulp van de log rank test. Het is belangrijk op te merken dat er verschillende varianten van de log rank test statistiek bestaan die door verschillende statistische rekenpakketten worden geïmplementeerd (b.v. SAS, R 4,6). Wij presenteren hier één versie die nauw verbonden is met de statistiek van de chi-kwadraattoets en die het waargenomen aantal voorvallen vergelijkt met het verwachte aantal voorvallen op elk tijdstip gedurende de follow-upperiode.
Voorbeeld:
Een kleine klinische studie wordt uitgevoerd om twee combinatiebehandelingen bij patiënten met gevorderde maagkanker te vergelijken. Twintig deelnemers met stadium IV-maagkanker die instemmen met deelname aan het onderzoek, krijgen willekeurig chemotherapie vóór de operatie of chemotherapie na de operatie. Het primaire resultaat is overlijden en de deelnemers worden gevolgd tot 48 maanden (4 jaar) na hun inschrijving voor de proef. De ervaringen van de deelnemers aan elke arm van de proef zijn hieronder weergegeven.
|
Chemotherapie vóór operatie |
|
Chemotherapie na operatie |
||
|---|---|---|---|---|
|
Maand van overlijden |
Maand van overlijden |
|||
|
Maand van overlijden |
Maand van laatste contact |
|
Maand van overlijden |
Maand van laatste contact |
|
8 |
8 |
|
33 |
48 |
|
12 |
32 |
|
28 |
48 |
|
26 |
20 |
|
41 |
25 |
|
14 |
40 |
|
|
37 |
|
21 |
|
|
|
48 |
|
27 |
|
|
|
25 |
|
|
|
|
|
43 |
Zes deelnemers in de groep met chemotherapie vóór operatie overlijden in de loop van de follow-vergeleken met drie deelnemers in de chemotherapie na de operatie groep. Andere deelnemers in elke groep worden gedurende een verschillend aantal maanden gevolgd, sommige tot het einde van de studie op 48 maanden (in de chemotherapie na chirurgie groep). Met behulp van de hierboven geschetste procedures construeren wij eerst levenscycli voor elke behandelingsgroep volgens de Kaplan-Meier-methode.
Levensduur tabel voor groep die chemotherapie kreeg voor de operatie
|
Tijd, Maanden |
Aantal risicogroepen Nt |
Aantal sterfgevallen Dt |
Aantal gecensureerde Ct |
Overlevingskans
|
|---|---|---|---|---|
|
0 |
10 |
|
|
1 |
|
8 |
10 |
1 |
1 |
0.900 |
|
12 |
8 |
1 |
|
0.788 |
|
14 |
7 |
1 |
|
0.675 |
|
20 |
6 |
|
1 |
0.675 |
|
21 |
5 |
1 |
|
0.540 |
|
26 |
4 |
1 |
|
0.405 |
|
27 |
3 |
1 |
|
0.270 |
|
32 |
2 |
|
1 |
0.270 |
|
40 |
1 |
|
1 |
0.270 |
Levensduur tabel voor groep die chemotherapie krijgt na operatie
|
Tijd, Maanden |
Aantal risicogevallen Nt |
Aantal sterfgevallen Dt |
Aantal gecensureerde Ct |
Overlevingskans
|
|---|---|---|---|---|
|
0 |
10 |
|
|
1 |
|
25 |
10 |
|
2 |
1.000 |
|
28 |
8 |
1 |
|
0.875 |
|
33 |
7 |
1 |
|
0.750 |
|
37 |
6 |
|
1 |
0.750 |
|
41 |
5 |
1 |
|
0.600 |
|
43 |
4 |
|
1 |
0.600 |
|
48 |
3 |
|
3 |
0,600 |
De twee overlevingscurven zijn hieronder weergegeven.
Overleving in elke behandelingsgroep
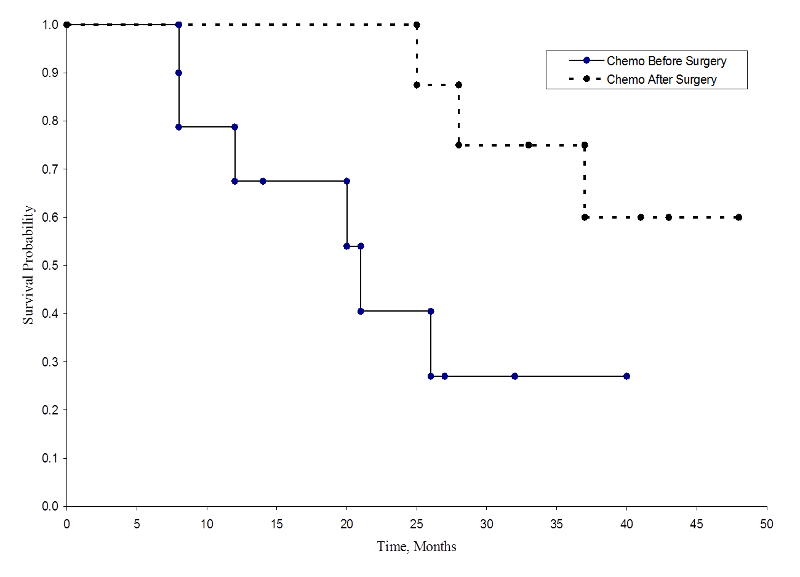
De overlevingskansen voor de chemotherapie na de operatiegroep zijn hoger dan de overlevingskansen voor de chemotherapie voor de operatiegroep, wat duidt op een overlevingsvoordeel. Deze overlevingskrommen zijn echter geschat op basis van kleine steekproeven. Om de overleving tussen groepen te vergelijken kunnen we de log rank test gebruiken. De nulhypothese is dat er geen verschil is in overleving tussen de twee groepen of dat er geen verschil is tussen de populaties in de kans op overlijden op enig moment. De log rank test is een niet-parametrische test en maakt geen veronderstellingen over de overlevingsdistributies. In wezen vergelijkt de logaranktest het waargenomen aantal voorvallen in elke groep met wat zou worden verwacht indien de nulhypothese waar zou zijn (d.w.z, als de overlevingskrommen identiek zouden zijn).
H0: De twee overlevingskrommen zijn identiek (of S1t = S2t) versus H1: De twee overlevingskrommen zijn niet identiek (of S1t ≠ S2t, op elk tijdstip t) (α=0,05).
De log rank statistiek is bij benadering verdeeld als een chi-kwadraat teststatistiek. Er zijn verschillende vormen van de teststatistiek, en zij verschillen in de wijze waarop zij worden berekend. Wij gebruiken de volgende vorm:
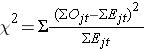
waarbij ΣOjt de som is van het waargenomen aantal voorvallen in de jde groep in de tijd (bv. j=1,2) en ΣEjt de som is van het verwachte aantal voorvallen in de jde groep in de tijd.
De sommen van het waargenomen en het verwachte aantal voorvallen worden berekend voor elke voorvaltijd en opgeteld voor elke vergelijkingsgroep. De log-rangstatistiek heeft vrijheidsgraden gelijk aan k-1, waarbij k het aantal vergelijkingsgroepen voorstelt. In dit voorbeeld is k=2, zodat de teststatistiek 1 vrijheidsgraad heeft.
Om de teststatistiek te berekenen hebben we het waargenomen en het verwachte aantal voorvallen op elk tijdstip van de gebeurtenis nodig. Het geobserveerde aantal gebeurtenissen is afkomstig van de steekproef en het verwachte aantal gebeurtenissen wordt berekend ervan uitgaande dat de nulhypothese waar is (d.w.z. dat de overlevingscurven identiek zijn).
Om de verwachte aantallen gebeurtenissen te genereren, ordenen wij de gegevens in een tabel met rijen die elk tijdstip van de gebeurtenis vertegenwoordigen, ongeacht de groep waarin de gebeurtenis zich heeft voorgedaan. Wij houden ook de groepstoewijzing bij. Vervolgens schatten wij de proportie voorvallen die zich op elk tijdstip voordoen (Ot/Nt) met gebruikmaking van gegevens van beide groepen gecombineerd onder de veronderstelling dat er geen verschil in overleving is (d.w.z. ervan uitgaande dat de nulhypothese waar is). Wij vermenigvuldigen deze schattingen met het aantal deelnemers dat op dat tijdstip risico loopt in elk van de vergelijkingsgroepen (N1t en N2t voor respectievelijk groep 1 en groep 2).
Specifiek berekenen wij voor elk tijdstip van de gebeurtenis t, het aantal dat risico loopt in elke groep, Njt (waarbij j de groep aangeeft, j=1, 2) en het aantal gebeurtenissen (sterfgevallen), Ojt , in elke groep. De onderstaande tabel bevat de informatie die nodig is om de log rank test uit te voeren om de bovenstaande overlevingskrommen te vergelijken. Groep 1 vertegenwoordigt de chemotherapie vóór de operatie groep, en groep 2 vertegenwoordigt de chemotherapie na de operatie groep.
Gegevens voor Log Rank Test om overlevingskrommen te vergelijken
|
Tijd, Maanden |
Aantal risicogevallen in groep 1
N1t |
Aantal risicogevallen in groep 2
N2t |
Aantal voorvallen (sterfgevallen) in groep 1
O1t |
Aantal voorvallen (sterfgevallen) in groep 2
N2t |
Aantal voorvallen (sterfgevallen) in groep 1
O1t Gebeurtenissen (Sterfgevallen) in groep 2 O2t |
|---|---|---|---|---|---|
|
8 |
10 |
10 |
1 |
0 |
|
|
12 |
8 |
10 |
1 |
0 |
|
|
14 |
7 |
10 |
1 |
0 |
|
|
21 |
5 |
10 |
1 |
0 |
|
|
26 |
4 |
8 |
1 |
0 |
|
|
27 |
3 |
8 |
1 |
0 |
|
|
28 |
2 |
8 |
0 |
1 |
|
|
33 |
1 |
7 |
0 |
1 |
|
|
41 |
0 |
5 |
0 |
1 |
Vervolgens tellen we het aantal risicopersonen bij elkaar op, Nt = N1t+N2t, op elk tijdstip van de gebeurtenis en het aantal waargenomen voorvallen (sterfgevallen), Ot = O1t+O2t, op elk tijdstip van de gebeurtenis. Vervolgens berekenen wij het verwachte aantal voorvallen in elke groep. Het verwachte aantal voorvallen wordt op elk tijdstip van de gebeurtenis als volgt berekend:
E1t = N1t*(Ot/Nt) voor groep 1 en E2t = N2t*(Ot/Nt) voor groep 2. De berekeningen staan in onderstaande tabel.
Verwachte aantallen gebeurtenissen in elke groep
|
Tijd, Maanden |
Aantal risicogroepen in groep 1 N1t |
Aantal risicogroepen in groep 2 N2t |
Totaal aantal risicogroepen Nt |
Aantal voorvallen in groep 1 O1t |
Aantal voorvallen in groep 2 O2t |
Totaal aantal voorvallen Ot |
Verwacht aantal gebeurtenissen in Groep 1 E1t = N1t*(Ot/Nt) |
Verwacht aantal gebeurtenissen in Groep 2 E2t = N2t*(Ot/Nt) |
|---|---|---|---|---|---|---|---|---|
|
8 |
10 |
10 |
20 |
1 |
0 |
1 |
0.500 |
0.500 |
|
12 |
8 |
10 |
18 |
1 |
0 |
1 |
0.444 |
0.556 |
|
14 |
7 |
10 |
17 |
1 |
0 |
1 |
0.412 |
0.588 |
|
21 |
5 |
10 |
15 |
1 |
0 |
1 |
0.333 |
0.667 |
|
26 |
4 |
8 |
12 |
1 |
0 |
1 |
0.333 |
0.667 |
|
27 |
3 |
8 |
11 |
1 |
0 |
1 |
0.273 |
0.727 |
|
28 |
2 |
8 |
10 |
0 |
1 |
1 |
0.200 |
0.800 |
|
33 |
1 |
7 |
8 |
0 |
1 |
1 |
0.125 |
0.875 |
|
41 |
0 |
5 |
5 |
0 |
1 |
1 |
0.000 |
1.000 |
Vervolgens tellen we de waargenomen aantallen gebeurtenissen in elke groep (∑O1t en ΣO2t) en de verwachte aantallen gebeurtenissen in elke groep (ΣE1t en ΣE2t) op in de tijd. Deze staan in de onderste rij van de volgende tabel.
Totaal waargenomen en verwachte aantallen waarnemingen in elke groep
|
Tijd, Maanden |
Aantal risicogroepen in groep 1 N1t |
Aantal risicogroepen in groep 2 N2t |
Totaal aantal risicogroepen Nt |
Aantal voorvallen in groep 1 O1t |
Aantal voorvallen in groep 2 O2t |
Totaal aantal voorvallen Ot |
Verwacht aantal gebeurtenissen in Groep 1 E1t = N1t*(Ot/Nt) |
Verwacht aantal gebeurtenissen in Groep 2 E2t = N2t*(Ot/Nt) |
|---|---|---|---|---|---|---|---|---|
|
8 |
10 |
10 |
20 |
1 |
0 |
1 |
0.500 |
0.500 |
|
12 |
8 |
10 |
18 |
1 |
0 |
1 |
0.444 |
0.556 |
|
14 |
7 |
10 |
17 |
1 |
0 |
1 |
0.412 |
0.588 |
|
21 |
5 |
10 |
15 |
1 |
0 |
1 |
0.333 |
0.667 |
|
26 |
4 |
8 |
12 |
1 |
0 |
1 |
0.333 |
0.667 |
|
27 |
3 |
8 |
11 |
1 |
0 |
1 |
0.273 |
0.727 |
|
28 |
2 |
8 |
10 |
0 |
1 |
1 |
0.200 |
0.800 |
|
33 |
1 |
7 |
8 |
0 |
1 |
1 |
0.125 |
0.875 |
|
41 |
0 |
5 |
5 |
0 |
1 |
1 |
0.000 |
1.000 |
|
|
6 |
3 |
|
2.620 |
6,380 |
We kunnen nu de teststatistiek berekenen:
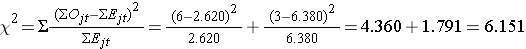
De teststatistiek is bij benadering verdeeld als chi-kwadraat met 1 graad van vrijheid. De kritische waarde voor de test kan dus worden gevonden in de tabel Kritische waarden van de Χ2-verdeling.
Voor deze test luidt de beslissingsregel: Verwerp H0 als Χ2 > 3,84. We zien dat Χ2 = 6,151, wat meer is dan de kritische waarde van 3,84. Daarom verwerpen wij H0. We hebben significant bewijs, α=0,05, om aan te tonen dat de twee overlevingskrommen verschillend zijn.
Voorbeeld:
Een onderzoeker wil de werkzaamheid evalueren van een korte interventie om alcoholgebruik tijdens de zwangerschap te voorkomen. Zwangere vrouwen met een voorgeschiedenis van zwaar alcoholgebruik worden voor de studie gerekruteerd en krijgen willekeurig ofwel de korte interventie gericht op onthouding van alcohol ofwel de standaard prenatale zorg. De uitkomst van de studie is terugval in drinken. Vrouwen worden bij een zwangerschapsduur van ongeveer 18 weken voor de studie gerekruteerd en gedurende de gehele zwangerschap gevolgd tot de bevalling (ongeveer 39 weken zwangerschap). De gegevens worden hieronder weergegeven en geven aan of vrouwen terugvallen in drinken en zo ja, het tijdstip van hun eerste drinkpauze gemeten in het aantal weken vanaf de randomisatie. Voor vrouwen die niet hervallen, noteren we het aantal weken vanaf de randomisatie dat ze alcoholvrij zijn.
|
Standaard prenatale zorg |
|
Korte interventie |
||
|---|---|---|---|---|
|
Terugval |
Geen terugval |
|
Terugval |
Geen terugval |
|
19 |
20 |
|
16 |
21 |
|
6 |
19 |
|
21 |
15 |
|
5 |
17 |
|
7 |
18 |
|
4 |
14 |
|
|
18 |
|
|
|
|
|
5 |
De vraag die van belang is, is of er een verschil is in de tijd tot terugval tussen vrouwen die zijn toegewezen aan de standaard prenatale zorg en vrouwen die zijn toegewezen aan de korte interventie.
- Stap 1.
Hypothesen opstellen en significantieniveau bepalen.
H0: Terugvalvrije tijd is identiek tussen groepen versus
H1: Terugvalvrije tijd is niet identiek tussen groepen (α=0,05)
- Stap 2.
Selecteer de juiste teststatistiek.
De teststatistiek voor de log rang-test is
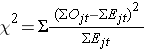
- Stap 3.
Stel de beslisregel op.
De teststatistiek volgt een chi-kwadraatverdeling, en dus vinden we de kritische waarde in de tabel met kritische waarden voor de Χ2-verdeling) voor df=k-1=2-1=1 en α=0,05. De kritische waarde is 3,84 en de beslisregel is om H0 af te wijzen als Χ2 > 3,84.
- Stap 4.
Bereken de teststatistiek.
Om de teststatistiek te berekenen, ordenen we de gegevens naar gebeurtenis (terugval)tijd en bepalen we het aantal vrouwen dat in elke behandelingsgroep risico loopt en het aantal dat op elk waargenomen terugvaltijdstip terugvalt. In de volgende tabel staat groep 1 voor vrouwen die standaard prenatale zorg krijgen en groep 2 voor vrouwen die de korte interventie krijgen.
|
Tijd, Weken > |
Aantal risicogroepen – groep 1 N1t |
Aantal risicogroepen – groep 2 N2t |
Aantal recidieven – groep 1 O1t |
Aantal recidieven – groep 2 O2t |
Aantal recidieven – groep 1 O1t |
Aantal recidieven – groep 2 O2t |
Aantal recidieven. Groep 2 O2t |
|---|---|---|---|---|---|---|---|
|
4 |
8 |
8 |
1 |
0 |
|||
|
5 |
7 |
8 |
1 |
0 |
|||
|
6 |
6 |
7 |
1 |
0 |
|||
|
7 |
5 |
7 |
0 |
1 |
|||
|
16 |
4 |
5 |
0 |
1 |
|||
|
19 |
3 |
2 |
1 |
0 |
|||
|
21 |
0 |
2 |
0 |
1 |
Vervolgens tellen we het aantal risicopersonen op, 
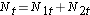, op elk tijdstip, het aantal waargenomen voorvallen (hervallen), 
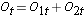, op elk tijdstip en bepalen we het verwachte aantal hervallen in elke groep op elk tijdstip met behulp van 
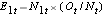en 
.
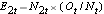Wij tellen vervolgens de waargenomen aantallen voorvallen in elke groep (ΣO1t en ΣO2t) en de verwachte aantallen voorvallen in elke groep (ΣE1t en ΣE2t) op over de tijd. De berekeningen voor de gegevens in dit voorbeeld zijn hieronder weergegeven.
| Tijd, Weken |
Aantal risicogroep 1 N1t |
Aantal risicogroep 2 N2t |
Totaal aantal risicogroepen Nt |
Aantal recidieven Groep 1 O1t |
Aantal recidieven Groep 2 O2t |
Totaal aantal van recidieven Ot |
Verwacht aantal recidieven in groep 1
|
Verwacht aantal recidieven in groep 2
|
|---|---|---|---|---|---|---|---|---|
|
4 |
8 |
8 |
16 |
1 |
0 |
1 |
0.500 |
0.500 |
|
5 |
7 |
8 |
15 |
1 |
0 |
1 |
0.467 |
0.533 |
|
6 |
6 |
7 |
13 |
1 |
0 |
1 |
0.462 |
0.538 |
|
7 |
5 |
7 |
12 |
0 |
1 |
1 |
0.417 |
0.583 |
|
16 |
4 |
5 |
9 |
0 |
1 |
1 |
0.444 |
0.556 |
|
19 |
3 |
2 |
5 |
1 |
0 |
1 |
0.600 |
0.400 |
|
21 |
0 |
2 |
2 |
0 |
1 |
1 |
0.000 |
1.000 |
|
|
|
|
|
4 |
3 |
|
2.890 |
4.110 |
We berekenen nu de teststatistiek:
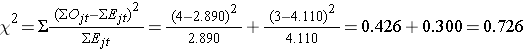
- Step 5.
Conclusie. Verwerp H0 niet omdat 0,726 < 3,84. We hebben geen statistisch significant bewijs bij α=0,05, om aan te tonen dat de tijd tot terugval verschilt tussen de groepen.
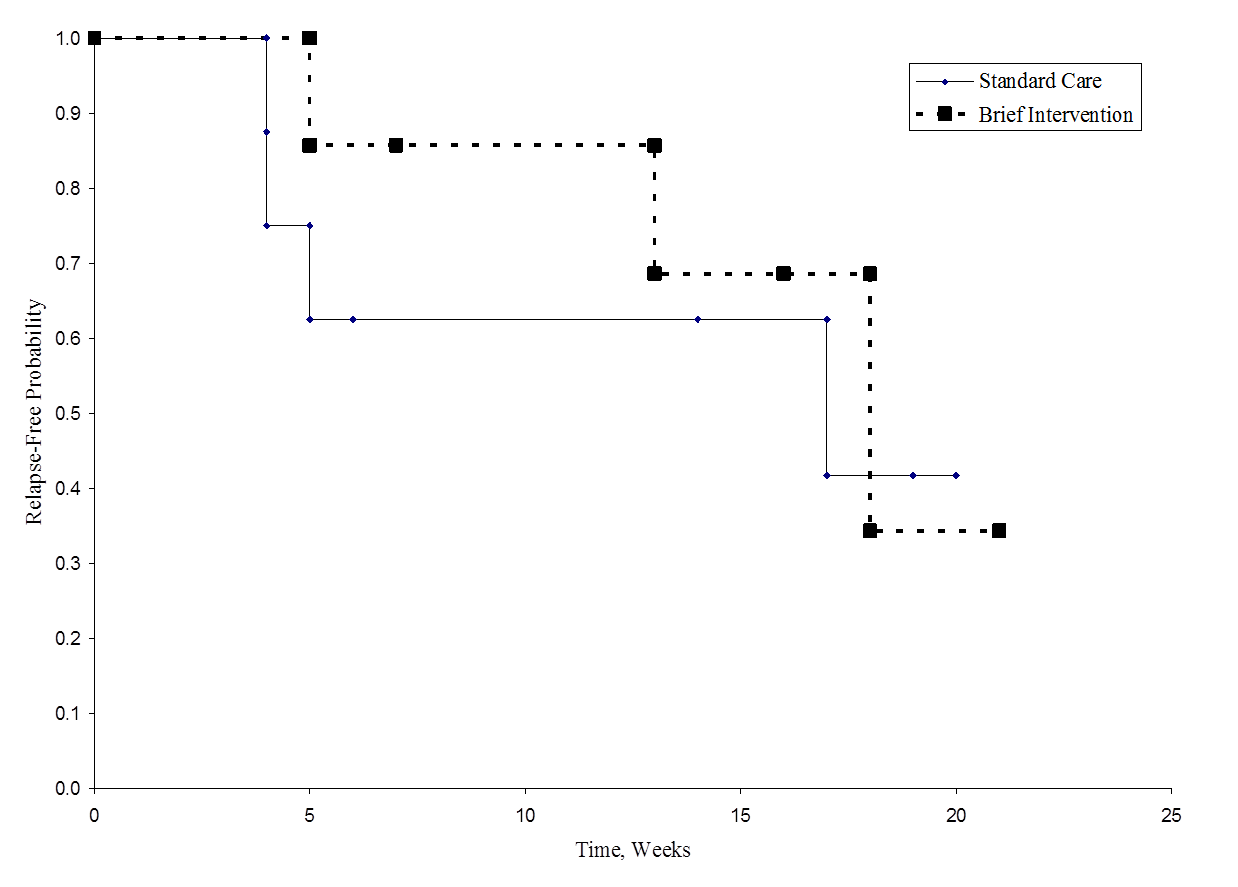
Onderstaande figuur toont de overleving (terugvalvrije tijd) in elke groep. Merk op dat de overlevingscurven niet veel scheiding vertonen, in overeenstemming met de niet-significante bevindingen in de hypothesetoets.
Relapse-Free Time in Each Group
Zoals opgemerkt, zijn er verschillende variaties van de log rank statistic. Sommige statistische rekenpakketten gebruiken de volgende teststatistiek voor de log rank test om twee onafhankelijke groepen te vergelijken:
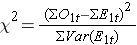
waarbij ΣO1t de som is van het waargenomen aantal voorvallen in groep 1, en ΣE1t de som is van het verwachte aantal voorvallen in groep 1, genomen over alle gebeurtenistijden. De noemer is de som van de varianties van de verwachte aantallen voorvallen op elk tijdstip, die als volgt wordt berekend:
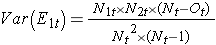
Er zijn andere versies van de log rank-statistiek en andere tests om overlevingsfuncties tussen onafhankelijke groepen te vergelijken.7-9 Een populaire test is bijvoorbeeld de gemodificeerde Wilcoxon-test, die gevoelig is voor grotere verschillen in risico’s eerder dan later in de follow-up.10
terug naar boven | vorige pagina | volgende pagina