In roomijs zijn kleine ronde ijskristallen belangrijk voor een zachte en romige textuur. In het algemeen geldt: hoe sneller de vriessnelheid, hoe kleiner de ijskristalgrootte. Voor sommige voedingsmiddelen is er echter een bovengrens voor de vriessnelheid. Als de vriessnelheid te hoog is, komen er mechanische spanningen op het voedselmateriaal te staan en kan vriesbreuk optreden. In enkele gevallen wordt het vriesproces gebruikt om materialen te structureren, zoals de traditionele Japanse kori-tofu schotel, of scaffolds zoals gebruikt in biologische weefselmanipulatie. Enkele jaren geleden onderzocht WUR, samen met de TU Delft en Unilever, het gebruik van vriesdrogen om soepgroenten te structureren. Hierbij bepaalt de ijskristalgrootte de grootte van de poriënruimte na het drogen, en helpt bij de rehydratatie van de groenten wanneer deze worden gemengd met de soep.
Relatie tussen ijskristalgrootte en vriessnelheid
Het is dus, vanuit het perspectief van diepvriesvoedselkwaliteit, belangrijk om goede kennis te hebben over de relatie tussen ijskristalgrootte en vriessnelheid. Er bestaan echter slechts enkele empirische verbanden tussen vriessnelheid en ijskristalgrootte. Bovendien worden er bij bereide levensmiddelen andere middelen gebruikt om de ijskristalgrootte te beheersen, zoals cryopectanten zoals suikers en antivrieseiwitten. Dit wijst erop dat er een interactie kan worden verwacht tussen de samenstelling van het voedsel, de vriessnelheid en de ijskristalgrootte, maar dat in de empirische relaties de afhankelijkheid van de samenstelling van het voedsel afwezig is. Daarom heeft Food & Biobased Research een onderzoeksproject opgezet dat zich richt op een meer theoretisch begrip van de relatie tussen vriessnelheid, samenstelling en ijskristalgrootte met behulp van geavanceerde computersimulaties.
Faseveldmodel voor ijskristalgroei
Om dit gedetailleerde begrip te verkrijgen moeten we in het micrometergebied van de microstructuur van voedingsmiddelen duiken, waar individuele ijskristallen worden opgelost in het ontwikkelde computermodel, waarin de kristalgroei wordt gemodelleerd als functie van de samenstelling van de matrix. De meest geavanceerde methode op dit gebied is het faseveldmodel, dat wij hebben gebruikt om de structurering te beschrijven van dispersies zoals schuimen en emulsies, gestabiliseerd met emulgatoren. In de faseveldmethode kan men gelijktijdig verschillende afzonderlijke elementen van dispersies modelleren, zoals emulsiedruppels, schuimbellen en kristallen. De methode laat gemakkelijk het uiteenvallen en coalescentie van deze gedispergeerde elementen toe.
De kracht van de methode ligt in de wijze waarop zij het grensvlak tussen gedispergeerde en continue fasen behandelt. De methode volgt hier het voorstel van een beroemde Nederlandse natuurkundige, vanderWaals, om het grensvlak op te nemen in een thermodynamisch raamwerk. Met behulp van de faseveldmethode hebben wij een computermodel geconstrueerd voor de beschrijving van ijskristallen in een sucrose-oplossing, waarvan het gedrag kan worden beschouwd als representatief voor consumptie-ijs3. In eerder onderzoek hebben wij reeds de thermodynamica van waterige sucrose-oplossingen4 opgehelderd, en ook de snelheid van watertransport in suikeroplossing via diffusie5. Voor deze materiaaleigenschappen hebben we dus voorspellende theorieën beschikbaar als functie van de sacharoseconcentratie voor het hele bereik van 0 tot 100%.
Vriessnelheid, samenstelling en ijskristalgrootte
Nadat we het computermodel hadden ontwikkeld, hebben we verschillende computersimulaties uitgevoerd om de relatie tussen vriessnelheid, samenstelling en ijskristalgrootte te onderzoeken. We zoomden in op een klein deel van het voedingsmateriaal en zaaiden verschillende kernen waarin ijskristallen konden groeien. Dit deel van het voedsel werd vervolgens onderworpen aan een reeks vriessnelheden. Er werden simulaties uitgevoerd voor twee verschillende sucroseconcentraties – en een veelheid van verschillende willekeurige posities van de kernen – om een aantal goede statistieken te verkrijgen.
Snapshots van deze computersimulaties zijn te zien in figuur 1. De donkerblauwe verspreide elementen zijn individuele ijskristallen. De vriessnelheid is niet erg hoog, zodat we kunnen aannemen dat de ijskristallen bij benadering bolvormig blijven. Voor een goed begrip van de simulatieresultaten is het belangrijk te weten dat ijskristallen geen suiker bevatten, zodat de groei van ijskristallen een toename van de suikerconcentratie in de nietbevroren fase impliceert. De verhoogde suikerconcentratie leidt tot een verhoging van het vriespunt, waardoor de continue matrix onbevroren blijft.

Figuur 1: Snapshots van de groei van ijskristallen in een suikeroplossing, verkregen via computersimulaties voor verschillende vriessnelheden (0,01, 0,03 en 0,10 K/s van boven naar beneden), waargenomen op verschillende tijdstippen (van links naar rechts). Let op de coalescentie van verschillende ijskristallen, vooral bij de lage vriessnelheid (boven)
Bij verder bevriezen kunnen de ijskristallen elkaar raken, waardoor de suikerconcentratie in de onbevroren vloeistof tussen hen in toeneemt, wat leidt tot vriespuntverlaging. Er ontstaat dan een vlak grensvlak. Als de vriessnelheid te laag is, hebben de suikers de tijd om uit de botsingszone te diffunderen en kunnen de kristallen samenklonteren. In het vroege vriesstadium, wanneer de plaatselijke toename van de suikerconcentratie als gevolg van de ijskristalgroei gering is, doen zich verschillende coalescentiefasen voor. In het latere stadium van bevriezing nadert de onbevroren matrix de glasachtige toestand – waar de diffusie van water en suiker tot stilstand komt en de ijskristalgroei stopt.
Uit de simulaties hebben we de gemiddelde ijskristalgrootte bepaald en uitgezet tegen de opgelegde vriessnelheid voor twee verschillende sucroseconcentraties. Deze resultaten zijn weergegeven in figuur 2.
In de simulatiegegevens kan een aanzienlijke spreiding worden waargenomen als gevolg van de stochastiek van het kerneningsproces. Door veel simulatieruns uit te voeren kan echter een betrouwbare machtswetrelatie door de gegevens worden gepast, die wordt weergegeven als de lijnen die door de datapunten lopen in figuur 2 (blz. 00). Uit de fitting blijkt dat de exponenten van de machtswet 0,31 en 0,18 zijn voor respectievelijk 10% en 15% suikeraanvangsconcentratie. Onze eerdere empirische relatie heeft een machtswet exponent van 0,25, waarvan werd aangenomen dat die onafhankelijk was van de samenstelling. Het feit dat de empirische waarde vrij dicht ligt bij de exponenten die we via simulatie hebben gevonden, is zeer bemoedigend. Bovendien is het vermeldenswaard dat voor het simulatiemodel geen parameteraanpassing nodig was, aangezien alle materiaal- en thermodynamische eigenschappen bekend zijn.
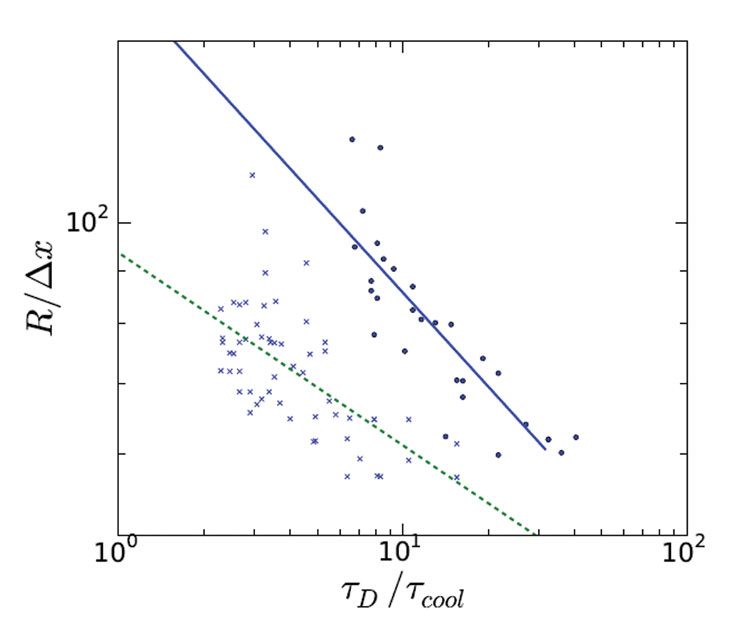
Figuur 2: Gemiddelde ijskristalgrootte versus de vriessnelheid, voor twee verschillende aanvankelijke suikerconcentraties (10% en 15%, aangegeven door de ononderbroken en onderbroken lijn). De straal wordt gemeten in eenheden van de computationele maas, die ongeveer 3 micron is, en de vriessnelheid 1/tcool wordt gemeten in termen van de snelheid van waterdiffusie 1/tD. (bij 0,01K/s als tD/tcool=1) De punten geven de gemiddelde grootte van een enkele simulatie aan. De lijnen stellen machtswetrelaties voor, passend bij de simulatiegegevens
Voedselkwaliteitsproblemen voor bevroren groenten en fruit
Food & Biobased Research concludeert dat het model wel degelijk een grote mate van realisme bezit. Bovendien zijn soortgelijke voorspellende theorieën over materiaal en thermodynamische eigenschappen beschikbaar voor veel andere voedingsmaterialen. Bijgevolg is het model in principe toepasbaar op een veelheid van andere voedingsmaterialen. Op basis hiervan hebben we een nieuw onderzoeksproject gestart dat het model verder ontwikkelt en aanpast aan bevroren voedingsmaterialen met een cellulaire structuur om bevroren voedselkwaliteitsproblemen voor fruit en groenten te onderzoeken. Het faseveldmodel zal worden ingebed in een multischaal model – omdat in voedingsmiddelen lokale verschillen in vriessnelheid zullen ontstaan – dat moet worden opgelost met een geavanceerde aanpak, waarbij het temperatuurprofiel wordt berekend op de productschaal, en de ijskristalgroei op de microschaal. Het computermodel op macroschaal zal het model op microschaal meerdere malen aanroepen voor een groot aantal locaties. Het microschaalmodel zal de lokale ijsfractie terugrapporteren, terwijl het macroschaalmodel de toegepaste temperatuurgradiënt aan het microschaalmodel zal doorgeven.
In dit nieuwe project, Food & Biobased Research, zullen we ons niet alleen richten op de initiële vriesstap, maar ook op de bevroren opslag. Tijdens de opslag kunnen temperatuurschommelingen optreden als gevolg van het mechanisch koelen, of het openen en sluiten van deuren. Aangenomen wordt dat door deze temperatuurschommelingen de ijskristallen verder kunnen groeien, wat nadelig is voor de productkwaliteit6. Wij willen nagaan of verlaging van de bewaartemperatuur het voedsel minder gevoelig maakt voor temperatuurschommelingen, en of zelfs een vermindering van het energieverbruik kan worden verkregen. Zelfs wanneer de bewaartemperatuur redelijk constant is, is er nog steeds sprake van een grovere verdeling van de ijskristallen tijdens de bewaring bij de conventionele omstandigheden van -18oC. Dit blijkt uit een vergelijking van levensmiddelen die zijn ingevroren met behulp van luchtstraalvriezen en invriezen met behulp van Pressure Shift Freezing (PSF). Aanvankelijk is de grootte van de ijskristallen die door middel van PSF worden verkregen veel kleiner dan bij conventioneel invriezen met lucht. Na enkele weken opslag wordt echter weinig verschil gevonden in de uiteindelijke ijskristalgrootteverdeling, wat erop wijst dat coarseening heeft plaatsgevonden tijdens de opslag van PSF voedingsmiddelen7.
Samenvattend is het nieuwe simulatiemodel een essentieel instrument om te duiken in mogelijke middelen voor de diepvriesvoedselindustrie om de textuur en de ijskristalgrootte van diepgevroren voedingsmiddelen te beheersen, op gebieden als 1) productformulering, 2) verwerkingscondities en vriessnelheid. Als de impact van formulering en verwerking op de kwaliteit van diepvriesvoedsel bekend is, kunnen nieuwe strategieën voor diepvriesopslag worden geëvalueerd vanwege hun impact op zowel productkwaliteit als energiebesparing.
- Voda, A., Homan, N., Witek, M., Duijster, A., van Dalen, G., van der Sman, R., Nijsse, J, van Vliet, L. Van As, H. & van Duynhoven, J. (2012). The impact of freeze-drying on microstructure and rehydration properties of carrot. Food Research International, 49(2), 687-693
- van der Sman, R. G. M., Voda, A., van Dalen, G., & Duijster, A. (2013). Ice crystal interspacing in frozen foods. Journal of Food Engineering, 116(2), 622-626
- van der Sman, R. G. M. (2016). Faseveldsimulaties van ijskristalgroei in suikeroplossingen. International Journal of Heat and Mass Transfer, 95, 153-161
- van der Sman, R. G. M., & Meinders, M. B. J. (2011). Prediction of the state diagram of starch water mixtures using the Flory-Huggins free volume theory. Soft Matter, 7(2), 429-442
- van der Sman, R. G. M., & Meinders, M. B. J. (2013). Vochtdiffusiviteit in voedingsmaterialen. Food chemistry, 138(2), 1265-1274
- Regand, A & Goff HD. “Structure and ice recrystallization in frozen stabilized ice cream model systems.” Food Hydrocolloids1 (2003): 95-102
- Fernández PP, Otero L, Martino MM ,Molina-García AD, & Sanz PD “High-pressure shift freezing: recrystallization during storage” European Food Research and Technology 5 (2008): 1367-1377
Over de auteur
Ruud van der Sman heeft een MSc in Toegepaste Natuurkunde aan de Technische Universiteit Delft en een PhD in Landbouwtechniek aan de Wageningen Universiteit. Hij werkt als senior onderzoeker bij Food & Biobased Research, en als deeltijd assistant professor bij Food Process Engineering – beide onderdeel van Wageningen UR (Universitair & Onderzoekscentrum). Zijn onderzoeksinteresses omvatten zachte materie fysica van voedselmaterialen, computermodellering van voedselstructurering op micrometerschaal, en fysiologische modellering. Zijn expertise in vlees omvat thermodynamica van waterhoudend vermogen, warmte- en massatransfer en postmortale fysiologie. www.wageningenur.nl/en/fbr