Een elektromagnetisch metamateriaal beïnvloedt elektromagnetische golven die botsen op of in wisselwerking staan met zijn structurele kenmerken, die kleiner zijn dan de golflengte. Om zich te gedragen als een homogeen materiaal dat nauwkeurig wordt beschreven door een effectieve brekingsindex, moeten de kenmerken veel kleiner zijn dan de golflengte.

Voor microgolfstraling zijn de kenmerken in de orde van millimeters. Microgolf metamaterialen zijn meestal opgebouwd als arrays van elektrisch geleidende elementen (zoals lussen van draad) die geschikte inductieve en capacitieve eigenschappen hebben. Veel microgolfmetamaterialen maken gebruik van split-ring resonatoren.

Fotonische metamaterialen zijn gestructureerd op nanometerschaal en manipuleren licht bij optische frequenties. Fotonische kristallen en frequentieselectieve oppervlakken zoals diffractieroosters, diëlektrische spiegels en optische coatings vertonen gelijkenissen met subgolflengte gestructureerde metamaterialen. Deze worden echter meestal beschouwd als verschillend van metamaterialen, omdat hun functie ontstaat door diffractie of interferentie en dus niet kan worden benaderd als een homogeen materiaal. Materiaalstructuren zoals fotonische kristallen zijn echter effectief in het zichtbare lichtspectrum. Het midden van het zichtbare spectrum heeft een golflengte van ongeveer 560 nm (voor zonlicht). Fotonische kristalstructuren zijn over het algemeen half zo groot of kleiner, namelijk <280 nm.

Plasmonische metamaterialen maken gebruik van oppervlakteplasmonen, dat zijn pakketjes elektrische lading die collectief oscilleren aan de oppervlakken van metalen bij optische frequenties.

Frequentieselectieve oppervlakken (FSS) kunnen subgolflengte-eigenschappen vertonen en staan bekend onder de namen kunstmatige magnetische geleiders (AMC) of High Impedance Surfaces (HIS). FSS vertonen inductieve en capacitieve kenmerken die rechtstreeks verband houden met hun subgolflengtestructuur.

Elektromagnetische metamaterialen kunnen als volgt in verschillende klassen worden onderverdeeld:

Negatieve brekingsindexEdit

Een vergelijking van de breking in een linkshandig metamateriaal met die in een normaal materiaal

Negatieve-index-metamaterialen (NIM) worden gekarakteriseerd door een negatieve brekingsindex. Andere termen voor NIMs zijn “linkshandige media”, “media met een negatieve brekingsindex”, en “achterwaartse-golf media”. NIMs waar de negatieve brekingsindex ontstaat uit gelijktijdig negatieve permittiviteit en negatieve permeabiliteit zijn ook bekend als dubbel negatieve metamaterialen of dubbel negatieve materialen (DNG).

Aannemende dat een materiaal goed benaderd wordt door een reële permittiviteit en permeabiliteit, is de relatie tussen permittiviteit ϵ r {\displaystyle \epsilon _{r}}

, doorlatendheid μ r {\displaystyle \mu _{r}}

en brekingsindex n wordt gegeven door n = ± ϵ r μ r {\displaystyle \scriptstyle n= {pm {\sqrt {\epsilon _{\mathrm {r}} mu _{\mathrm {r} }}}}

. Alle bekende niet-metamateriaal doorzichtige materialen (glas, water, …) bezitten positieve ϵ r {\displaystyle \epsilon _{r}}

en μ r {\displaystyle \mu _{r}}

. Bij conventie wordt de positieve vierkantswortel gebruikt voor n. Sommige technische metamaterialen hebben echter ϵ r {\displaystyle \epsilon _{r}}

en μ r < 0 {\displaystyle \displaystyle _{r}<0}

. Omdat het product ϵ r μ r {\displaystyle \epsilon _{r}\mu _{r}}

positief is, is n reëel. In dat geval moet voor n de negatieve vierkantswortel worden genomen. Wanneer zowel ϵ r {\displaystyle \epsilon _{r}}

en μ r {\displaystyle \mu _{r}}

positief (negatief) zijn, reizen golven in voorwaartse (achterwaartse) richting. Elektromagnetische golven kunnen zich niet voortplanten in materialen met ϵ r {\displaystyle \epsilon _{r}}

en μ r {\displaystyle \mu _{r}}

van tegengesteld teken als de brekingsindex denkbeeldig wordt. Dergelijke materialen zijn ondoorzichtig voor elektromagnetische straling en voorbeelden zijn plasmonische materialen zoals metalen (goud, zilver, …).

De voorgaande overwegingen zijn simplistisch voor reële materialen, die een complexe waarde van ϵ r moeten hebben {Displaystyle \epsilon _{r}}

en μ r {\displaystyle \epsmu _{r}}

. De reële delen van zowel ϵ r {\displaystyle \epsilon _{r}}

en μ r {\displaystyle \mu _{r}}

hoeven niet negatief te zijn opdat een passief materiaal negatieve breking zou vertonen. Een negatieve brekingsindex voor circulair gepolariseerde golven kan immers ook het gevolg zijn van chiraliteit. Metamaterialen met negatieve n hebben talrijke interessante eigenschappen:

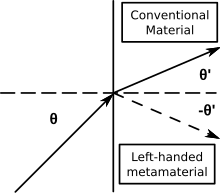
• De wet van Snell (n1sinθ1 = n2sinθ2) beschrijft nog steeds de breking, maar omdat n2 negatief is, liggen invallende en afgebogen stralen aan dezelfde kant van de oppervlaknormaal bij een grensvlak van materialen met positieve en negatieve index.
• Cherenkovstraling wijst de andere kant op.
• De tijdgemiddelde Poyntingvector is antiparallel aan de fasesnelheid. Voor de voortplanting van golven (energie) moet echter een -µ gepaard gaan met een -ε om te voldoen aan de afhankelijkheid van het golfgetal van de materiaalparameters k c = ω μ ϵ {\displaystyle kc==\omega {\sqrt {\mu \epsilon }}
  

  .

Negatieve brekingsindex vloeit wiskundig voort uit het vectortriplet E, H en k.

Voor vlakke golven die zich voortplanten in elektromagnetische metamaterialen volgen het elektrisch veld, het magnetisch veld en de golfvector een linkerhandregel, het omgekeerde van het gedrag van conventionele optische materialen.

Tot op heden vertonen alleen metamaterialen een negatieve brekingsindex.

Enkel negatiefEdit

Single negative (SNG) metamaterialen hebben of een negatieve relatieve permittiviteit (εr) of een negatieve relatieve permeabiliteit (µr), maar niet beide. Zij gedragen zich als metamaterialen wanneer zij gecombineerd worden met een andere, complementaire SNG, gezamenlijk optredend als een DNG.

Epsilon negatieve media (ENG) vertonen een negatieve εr terwijl µr positief is. Vele plasma’s vertonen deze eigenschap. Zo zijn edele metalen zoals goud of zilver ENG in het infrarode en zichtbare spectrum.

Mu-negatieve media (MNG) vertonen een positieve εr en negatieve µr. Gyrotropische of gyromagnetische materialen vertonen deze eigenschap. Een gyrotroop materiaal is een materiaal dat door de aanwezigheid van een quasistatisch magnetisch veld is veranderd, waardoor een magneto-optisch effect mogelijk wordt. Een magneto-optisch effect is een verschijnsel waarbij een elektromagnetische golf zich door een dergelijk medium voortplant. In een dergelijk materiaal kunnen links- en rechtsdraaiende elliptische polarisaties zich met verschillende snelheden voortplanten. Wanneer licht door een laag magneto-optisch materiaal wordt gestuurd, wordt het resultaat het Faraday-effect genoemd: het polarisatievlak kan worden geroteerd, waardoor een Faraday-rotator wordt gevormd. Het resultaat van een dergelijke reflectie staat bekend als het magneto-optische Kerr-effect (niet te verwarren met het niet-lineaire Kerr-effect). Twee gyrotropische materialen met omgekeerde draairichtingen van de twee hoofdpolarisaties worden optische isomeren genoemd.

Het samenvoegen van een plaat van ENG-materiaal en een plaat van SNG-materiaal resulteerde in eigenschappen als resonanties, anomale tunneling, doorzichtigheid en nulreflectie. Net als materialen met negatieve index zijn SNG’s van nature dispersief, zodat hun εr, µr en brekingsindex n, een functie van frequentie zijn.

HyperbolischEdit

Hyperbolische metamaterialen (HMM’s) gedragen zich als een metaal voor bepaalde polarisatie of richting van lichtvoortplanting en gedragen zich als een diëlektricum voor de andere als gevolg van de negatieve en positieve permittiviteitstensorcomponenten, wat extreme anisotropie geeft. De dispersierelatie van het materiaal in de golfvectorruimte vormt een hyperboloïde en daarom wordt het een hyperbolisch metamateriaal genoemd. De extreme anisotropie van HMM’s leidt tot gerichte voortplanting van licht binnen en op het oppervlak. HMM’s hebben verschillende potentiële toepassingen laten zien, zoals detectie, beeldvorming, het sturen van optische signalen, versterkte plasmon resonantie effecten.

BandgapEdit

Elektromagnetische bandkloof metamaterialen (EBG of EBM) regelen de voortplanting van licht. Dit wordt bereikt met fotonische kristallen (PC) of linkshandige materialen (LHM). PC’s kunnen de voortplanting van licht geheel verbieden. Beide klassen kunnen de voortplanting van licht in specifieke, ontworpen richtingen toestaan en beide kunnen worden ontworpen met bandgaps bij gewenste frequenties. De periodegrootte van EBG’s is een aanzienlijke fractie van de golflengte, waardoor constructieve en destructieve interferentie ontstaat.

PC onderscheiden zich van sub-golflengte structuren, zoals afstembare metamaterialen, omdat de PC zijn eigenschappen ontleent aan zijn bandkloofkarakteristieken. PC’s hebben een afmeting die overeenkomt met de golflengte van het licht, in tegenstelling tot andere metamaterialen die een sub-golflengte structuur vertonen. Bovendien werken PC’s door licht af te buigen. Metamaterialen maken daarentegen geen gebruik van diffractie.

PC’s hebben periodieke insluitsels die golfvoortplanting tegengaan door de destructieve interferentie van verstrooiing van de insluitsels. De fotonische bandkloof eigenschap van PCs maakt ze de elektromagnetische analogon van elektronische halfgeleiderkristallen.

EBGs hebben als doel het creëren van hoge kwaliteit, laag verlies, periodieke, diëlektrische structuren. Een EBG beïnvloedt fotonen op dezelfde manier als halfgeleidermaterialen elektronen beïnvloeden. PC’s zijn het perfecte bandgap-materiaal, omdat zij geen lichtvoortplanting toelaten. Elke eenheid van de voorgeschreven periodieke structuur werkt als een atoom, zij het van een veel grotere omvang.

EBG’s zijn ontworpen om de voortplanting van een toegewezen bandbreedte van frequenties te verhinderen, voor bepaalde aankomsthoeken en polarisaties. Diverse geometrieën en structuren zijn voorgesteld om de speciale eigenschappen van EBG’s te fabriceren. In de praktijk is het onmogelijk een foutloos EBG-apparaat te bouwen.

EBG’s zijn vervaardigd voor frequenties variërend van enkele gigahertz (GHz) tot enkele terahertz (THz), radio-, microgolf- en midden-infraroodfrequentiegebieden. EBG-toepassingsontwikkelingen omvatten een transmissielijn, houtpalen gemaakt van vierkante diëlektrische staven en verschillende soorten antennes met lage versterking.

Dubbel positief mediumEdit

Dubbel positieve mediums (DPS) komen wel voor in de natuur, zoals natuurlijk voorkomende diëlektrica. Permittiviteit en magnetische permeabiliteit zijn beide positief en de golfvoortplanting is in de voorwaartse richting. Er zijn kunstmatige materialen gefabriceerd die DPS, ENG en MNG eigenschappen combineren.

Bi-isotroop en bianisotroopEdit

Het categoriseren van metamaterialen in dubbel of enkel negatief, of dubbel positief, gaat er normaal van uit dat het metamateriaal onafhankelijke elektrische en magnetische reacties heeft, beschreven door ε en µ. Echter, in veel gevallen veroorzaakt het elektrische veld magnetische polarisatie, terwijl het magnetische veld elektrische polarisatie induceert, bekend als magneto-elektrische koppeling. Dergelijke media worden bi-isotroop genoemd. Media die magneto-elektrische koppeling vertonen en anisotroop zijn (wat het geval is voor vele metamateriaalstructuren), worden bi-anisotroop genoemd.

Vier materiaalparameters zijn intrinsiek voor magneto-elektrische koppeling van bi-isotrope media. Het zijn de elektrische (E) en magnetische (H) veldsterktes, en de elektrische (D) en magnetische (B) fluxdichtheden. Deze parameters zijn respectievelijk ε, µ, κ en χ of permittiviteit, permeabiliteit, chiraliteitssterkte, en de Tellegen-parameter. In dit type media variëren de materiaalparameters niet met veranderingen langs een geroteerd coördinatenstelsel van metingen. In die zin zijn zij invariant of scalair.

De intrinsieke magneto-elektrische parameters, κ en χ, beïnvloeden de fase van de golf. Het effect van de chiraliteitsparameter is het splitsen van de brekingsindex. In isotrope media resulteert dit alleen in golfvoortplanting indien ε en µ hetzelfde teken hebben. In bi-isotrope media, waarbij χ wordt verondersteld nul te zijn, en κ een niet-nul waarde, ontstaan andere resultaten. Er kan een achterwaartse golf of een voorwaartse golf optreden. Of er kunnen twee voorwaartse golven of twee achterwaartse golven optreden, afhankelijk van de sterkte van de chiraliteitsparameter.

In het algemene geval luiden de constitutieve relaties voor bi-anisotrope materialen D = ϵ E + ξ H , {\displaystyle \mathbf {D} =\epsilon \mathbf {E} +\xi \mathbf {H} ,}

{\displaystyle \mathbf {D} =\epsilon \mathbf {E} +\B = ζ E + μ H , {\displaystyle \mathbf {B} =zeta \mathbf {E}

waarbij ϵ {\displaystyle \epsilon }

en μ {\displaystyle \mu }

zijn respectievelijk de permittiviteitstensor en de permeabiliteitstensor, terwijl ξ {\displaystyle \xi }

en ζ {{displaystyle \zeta }

zijn de twee magneto-elektrische tensoren. Indien het medium reciproke is, zijn permittiviteit en permeabiliteit symmetrische tensoren, en ξ = – ζ T = – i κ T {\displaystyle \xi =-\zeta ^{T}=-i\kappa ^{T}}

, waarbij κ {{\zeta \kappa }}

[kappa

de chirale tensor is die de chirale elektromagnetische en wederkerige magneto-elektrische respons beschrijft. De chirale tensor kan worden uitgedrukt als κ = 1 3 tr ( κ ) I + N + J {\displaystyle \kappa ={\tfrac {1}{3}}operatornaam {tr} (\kappa )I+N+J}

, waarbij tr ( κ ) {{\displaystyle \operatornaam {tr} (\kappa )}

is het spoor van κ {{\displaystyle \kappa }

, I is de eenheidsmatrix, N is een symmetrische spoorloze tensor, en J is een antisymmetrische tensor. Door een dergelijke decompositie kunnen we de reciproke bianisotrope respons classificeren en kunnen we de volgende drie hoofdklassen onderscheiden: (i) chirale media ( tr ( κ ) ≠ 0 , N ≠ 0 , J = 0 {\displaystyle \operatorname {tr} (\kappa )\neq 0,N\neq 0,J=0}

), ii) pseudochirale media ( tr ( κ ) = 0 , N ≠ 0 , J = 0 {\displaystyle \operatorname {tr} (\kappa )=0,N ≠ 0,J=0}

), (iii) omega media ( tr ( κ ) = 0 , N = 0 , J ≠ 0 {\displaystyle \operatorname {tr} (\kappa )=0,N=0,J ≠ 0}

).

ChiralEdit

Handigheid van metamaterialen is een potentiële bron van verwarring, omdat de metamateriaalliteratuur twee tegenstrijdige gebruiken van de termen links- en rechtshandig bevat. De eerste verwijst naar één van de twee circulair gepolariseerde golven die de voortplantingswijzen zijn in chirale media. De tweede heeft betrekking op het triplet van elektrisch veld, magnetisch veld en Poynting vector die ontstaan in negatief brekingsindex media, die in de meeste gevallen niet chiraal zijn.

In het algemeen is een chirale en/of bianisotrope elektromagnetische respons een gevolg van 3D geometrische chiraliteit: 3D-chirale metamaterialen worden samengesteld door het inbedden van 3D-chirale structuren in een gastmedium en zij vertonen chiraliteitsgerelateerde polarisatie-effecten zoals optische activiteit en circulair dichroïsme. Het concept van 2D-chiraliteit bestaat ook en men zegt dat een vlak voorwerp chiraal is als het niet kan worden gesuperponeerd op zijn spiegelbeeld tenzij het uit het vlak wordt getild. Bij 2D-chirale metamaterialen die anisotroop en verliesgevend zijn, is waargenomen dat zij richting asymmetrische transmissie (reflectie, absorptie) van circulair gepolariseerde golven vertonen als gevolg van circulair conversie dichrosim. Anderzijds kan bianisotrope respons ontstaan uit geometrische achirale structuren die noch 2D noch 3D intrinsieke chiraliteit bezitten. Plum en collega’s onderzochten magneto-elektrische koppeling ten gevolge van extrinsieke chiraliteit, waarbij de opstelling van een (achirale) structuur samen met de stralingsgolfvector verschilt van zijn spiegelbeeld, en observeerden grote, afstembare lineaire optische activiteit, niet-lineaire optische activiteit, speculaire optische activiteit en circulair conversie dichroïsme. Rizza et al. stelden 1D chirale metamaterialen voor waarbij de effectieve chirale tensor niet vanishing is indien het systeem geometrisch één-dimensionaal chiraal is (het spiegelbeeld van de gehele structuur kan er niet op gesuperponeerd worden door vertalingen zonder rotaties te gebruiken).

3D-chirale metamaterialen zijn opgebouwd uit chirale materialen of resonatoren waarin de effectieve chiraliteitsparameter κ { {{displaystyle \kappa }

\kappa

niet nul is. Golfvoortplantingseigenschappen in dergelijke chirale metamaterialen tonen aan dat negatieve breking kan worden gerealiseerd in metamaterialen met een sterke chiraliteit en positieve ϵ r {\displaystyle \epsilon _{r}}

en μ r {\displaystyle \mu _{r}}

. Dit komt omdat de brekingsindex n {\displaystyle n}

verschillende waarden heeft voor links en rechts circulair gepolariseerde golven, gegeven door

n = ± ϵ r μ r ± κ {\displaystyle n= {pm {\sqrt {\epsilon _{r}}\mu _{r}}}pm \kappa }

Het is te zien dat een negatieve index zal optreden voor één polarisatie als κ {\displaystyle n=pm {\displaystyle \kappa }

ϵ r μ r {\displaystyle {\sqrt {\epsilon _{r}mu _{r}}}}

. In dit geval is het niet noodzakelijk dat één van beide of beide ϵ r {\displaystyle \epsilon _{r}}

en μ r {\displaystyle \mu _{r}}

negatief zijn voor achterwaartse golfvoortplanting. Een negatieve brekingsindex als gevolg van chiraliteit werd voor het eerst gelijktijdig en onafhankelijk waargenomen door Plum et al. en Zhang et al. in 2009.

FSS gebaseerdEdit

Main article: Tunable metamaterials § Frequency selective surface based metamaterials

Frequency selective surface based metamaterials blokkeren signalen in de ene golfband en laten die in een andere golfband door. Zij zijn een alternatief geworden voor metamaterialen met een vaste frequentie. Zij maken een optionele verandering van frequenties in een enkel medium mogelijk, in plaats van de beperkende beperkingen van een vaste frequentierespons.