In de tutorial over gegeneraliseerde lineaire modellen hebben we geleerd over verschillende GLM’s zoals lineaire regressie, logistische regressie, enz. In deze tutorial van de TechVidvan’s R tutorial serie, gaan we in detail kijken naar lineaire regressie in R. We zullen leren wat R lineaire regressie is en hoe het te implementeren in R. We zullen kijken naar de kleinste kwadraat schattingsmethode en zullen ook leren hoe de nauwkeurigheid van het model te controleren.

Dus, zonder verdere ophef, laten we aan de slag gaan!

Lineaire regressie in R

Lineaire regressie in R is een methode die wordt gebruikt om de waarde van een variabele te voorspellen met behulp van de waarde(n) van een of meer input-voorspellende variabelen. Het doel van lineaire regressie is een lineair verband tot stand te brengen tussen de gewenste outputvariabele en de inputvoorspellers.

Het modelleren van een continue variabele Y als een functie van een of meer inputvoorspellingsvariabelen Xi, zodat de functie kan worden gebruikt om de waarde van Y te voorspellen wanneer alleen de waarden van Xi bekend zijn. De algemene vorm van een dergelijk lineair verband is:

Y=?0+?1 X

Hierbij is ?0 de intercept
en ?1 de helling.

Typen lineaire regressie in R

Er zijn twee typen lineaire regressie in R:

• Eenvoudige lineaire regressie
• Meervoudige lineaire regressie

Laten we deze eens één voor één bekijken.

Eenvoudige lineaire regressie in R

Eenvoudige lineaire regressie is gericht op het vinden van een lineair verband tussen twee continue variabelen. Het is belangrijk op te merken dat de relatie statistisch van aard is en niet deterministisch.

Een deterministische relatie is een relatie waarbij de waarde van de ene variabele nauwkeurig kan worden gevonden door gebruik te maken van de waarde van de andere variabele. Een voorbeeld van een deterministische relatie is die tussen kilometers en mijlen. Aan de hand van de kilometerwaarde kunnen we de afstand in mijlen nauwkeurig bepalen. Een statistische relatie is niet nauwkeurig en heeft altijd een voorspellingsfout. Met voldoende gegevens kunnen we bijvoorbeeld een verband vinden tussen de lengte en het gewicht van een persoon, maar er zal altijd een foutmarge zijn en er zullen uitzonderingsgevallen bestaan.

Het idee achter eenvoudige lineaire regressie is een lijn te vinden die het best past bij de gegeven waarden van beide variabelen. Deze lijn kan ons dan helpen de waarden van de afhankelijke variabele te vinden wanneer deze ontbreken.

Laten we dit bestuderen met behulp van een voorbeeld. We hebben een dataset bestaande uit de lengte en het gewicht van 500 mensen. Ons doel hier is een lineair regressiemodel op te stellen dat de relatie tussen lengte en gewicht zodanig formuleert dat wanneer wij lengte(Y) als invoer aan het model geven, het ons gewicht(X) kan teruggeven met een minimale marge of fout.

Y=b0+b1X

De waarden van b0 en b1 moeten zo worden gekozen dat zij de foutmarge minimaliseren. De foutenmetriek kan worden gebruikt om de nauwkeurigheid van het model te meten.

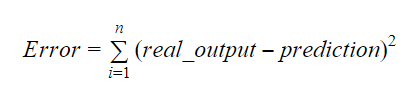
We kunnen de helling of de coëfficiënt berekenen als: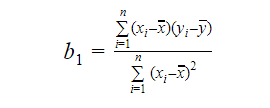

De waarde van b1 geeft ons inzicht in de aard van het verband tussen de afhankelijke en de onafhankelijke variabelen.

• Als b1 > 0, dan hebben de variabelen een positief verband, d.w.z. toename van x zal resulteren in een toename van y.
• Als b1 < 0, dan hebben de variabelen een negatief verband, d.w.z. toename van x zal resulteren in een afname van y.

De waarde van b0 of intercept kan als volgt worden berekend: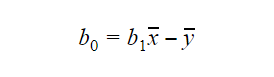
De waarde van b0 kan ook veel informatie geven over het model en omgekeerd.

Als x=0 niet in het model is opgenomen, dan is de voorspelling zonder b1 zinloos. Opdat het model op een bepaald punt alleen b0 en niet b1 zou bevatten, moet de waarde van x op dat punt 0 zijn. In gevallen zoals lengte kan x niet 0 zijn en de lengte van een persoon kan niet 0 zijn. Daarom is zo’n model zinloos met alleen b0.

Als de term b0 ontbreekt, zal het model door de oorsprong gaan, wat betekent dat de voorspelling en de regressiecoëfficiënt (helling) vertekend zullen zijn.

Meervoudige lineaire regressie in R

Meervoudige lineaire regressie is een uitbreiding van eenvoudige lineaire regressie. Bij meervoudige lineaire regressie willen we een lineair model maken dat de waarde van de doelvariabele kan voorspellen met behulp van de waarden van meerdere voorspellende variabelen. De algemene vorm van een dergelijke functie is als volgt:

Y=b0+b1X1+b2X2+…+bnXn

Beoordeling van de nauwkeurigheid van het model

Er zijn verschillende methoden om de kwaliteit en nauwkeurigheid van het model te beoordelen. Laten we een aantal van deze methoden een voor een bekijken.

R-Squared

De echte informatie in gegevens is de variantie die erin zit. R-kwadraat vertelt ons welk deel van de variatie in de doelvariabele (y) door het model wordt verklaard. Wij kunnen de R-kwadraat maatstaf van een model vinden met de volgende formule: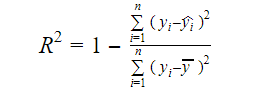

Waar,

• yi is de gepaste waarde van y voor waarneming i
• y is het gemiddelde van Y.

Een lagere waarde van R-kwadraat betekent een lagere nauwkeurigheid van het model. De R-kwadraatmaatstaf is echter niet noodzakelijk een doorslaggevende factor.

Gecorrigeerde R-Squared

Naarmate het aantal variabelen in het model toeneemt, neemt ook de R-kwadraatwaarde toe. Dit veroorzaakt ook fouten in de variatie die wordt verklaard door de nieuw toegevoegde variabelen. Daarom passen we de formule voor R kwadraat aan voor meerdere variabelen.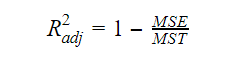
Hier staat de MSE voor Mean Standard Error die:

En MST staat voor Mean Standard Total die gegeven wordt door: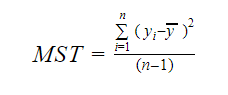

Waarbij, n het aantal waarnemingen is en q het aantal coëfficiënten.

Het verband tussen R-squared en adjusted R-squared is: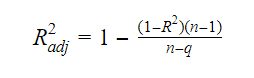

Standaardfout en F-statistiek

De standaardfout en de F-statistiek zijn beide maatstaven voor de kwaliteit van de fit van een model. De formules voor de standaardfout en de F-statistiek zijn:

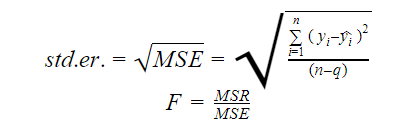
Waarbij MSR staat voor Mean Square Regression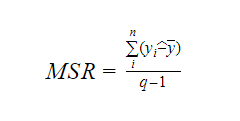

AIC en BIC

Akaike’s Informatiecriterium en Bayesiaans Informatiecriterium zijn maatstaven voor de kwaliteit van de fit van statistische modellen. Zij kunnen ook worden gebruikt als criteria voor de selectie van een model.

AIC=(-2)*ln(L)+2*k
BIC=(-2)*ln(L)+k*ln(n)

Waarbij,

• L de likelihood functie is,
• k het aantal modelparameters,
• n de steekproefgrootte.

lm functie in R

De lm() functie van R past lineaire modellen toe. Het kan regressie, en analyse van variantie en covariantie uitvoeren. De syntaxis van de lm-functie is als volgt:

lm(formula, data, subset, weights, na.action,method = "qr", model = TRUE, x = FALSE, y = FALSE, qr = TRUE,singular.ok = TRUE, offset, …)

Waar,

• formule een object is van de klasse “formule” en een symbolische voorstelling van het te fitten model,
• data het dataframe of de datalijst is die de variabelen in de formule bevat(data is een optioneel argument. Als het ontbreekt, haalt de functie de variabelen uit de omgeving),
• subset is een optionele vector die een subset van waarnemingen bevat die in de aanpassingsprocedure moeten worden gebruikt,
• weights is een optionele vector die de gewichten specificeert die in de aanpassingsprocedure moeten worden gebruikt,
• na.action is een functie die aangeeft wat er moet gebeuren wanneer NA’s in de gegevens worden aangetroffen,
• method geeft de methode voor de aanpassing van het model aan,
• model, x, y, en qr zijn logica’s die bepalen of overeenkomstige waarden al dan niet bij de uitvoer moeten worden geretourneerd. Deze waarden zijn:
• model: het modelkader
• x: de modelmatrix
• y: de respons
• qr: de qr-ontleding
• singular.ok is een logica die bepaalt of singuliere fits zijn toegestaan of niet,
• offset is een vooraf bekende voorspeller die in het model moet worden gebruikt,
• .

Praktisch voorbeeld van lineaire regressie in R

Dit is genoeg theorie voor nu. Laten we eens kijken hoe we dit alles kunnen implementeren. We gaan een lineair model fitten met behulp van lineaire regressie in R met behulp van de lm() functie. Nadien zullen we ook de kwaliteit van de fit van het model controleren. Laten we gebruik maken van de cars dataset die standaard wordt meegeleverd in het basispakket van R.

1. Laten we beginnen met een grafische analyse van de dataset om er meer vertrouwd mee te raken. Daartoe zullen we een scatterplot tekenen en nagaan wat deze ons over de gegevens vertelt.

We kunnen de functie scatter.smooth() gebruiken om een scatterplot voor de dataset te maken.

scatter.smooth(x=cars$speed,y=cars$dist,main="TechVidvan Dist ~ Speed")

Output

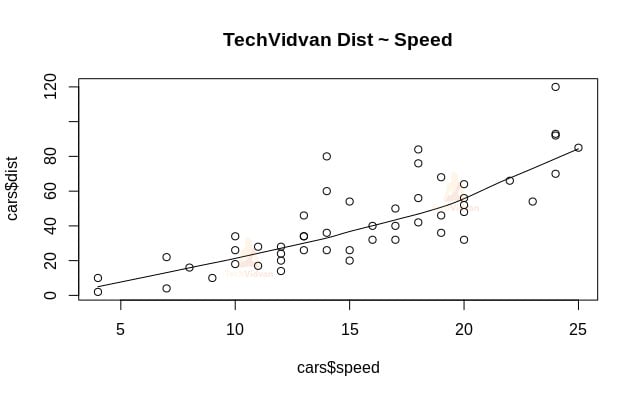
De scatterplot toont ons een positieve correlatie tussen afstand en snelheid. Het suggereert een lineair stijgend verband tussen de twee variabelen. Dit maakt de gegevens geschikt voor lineaire regressie, aangezien een lineair verband een basisveronderstelling is voor het fitten van een lineair model op gegevens.

2. Nu we hebben geverifieerd dat lineaire regressie geschikt is voor de gegevens, kunnen we de functie lm() gebruiken om er een lineair model op te fitten.

Linear_model <- lm(dist~speed,data=cars)print(Linear_model)

Uitvoer

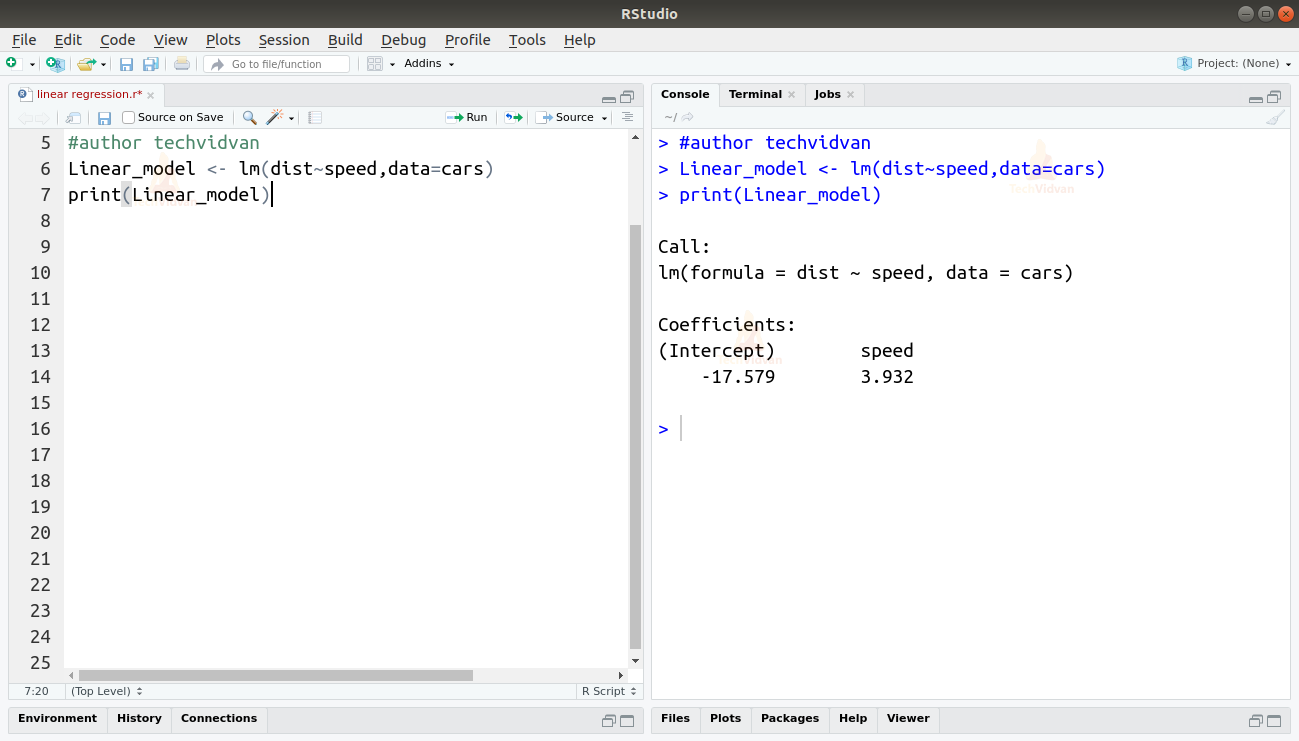
De uitvoer van de lm()-functie toont ons het intercept en de coëfficiënt van de snelheid. Het lineaire verband tussen afstand en snelheid is dus als volgt gedefinieerd:

Afstand=Intercept+coëfficiënt*snelheid

Afstand=-17,579+3,932*snelheid

3. Nu we een model hebben opgesteld, kunnen we de kwaliteit of goedheid van de “fit” controleren. Laten we beginnen met de samenvatting van het lineaire model te controleren met behulp van de functie summary().

summary(Linear_model)

Output

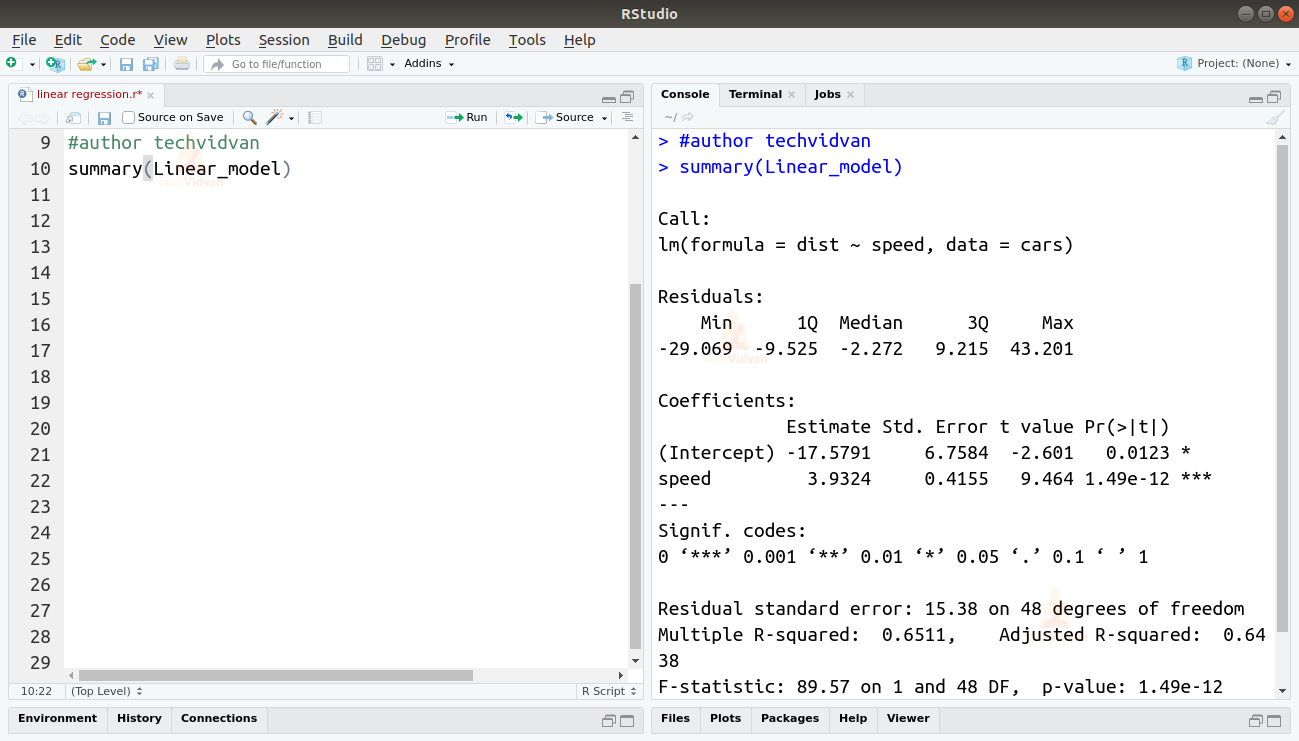
De functie summary() geeft ons een paar belangrijke maatstaven om de geschiktheid van het model te helpen diagnosticeren. De p-waarde is een belangrijke maatstaf voor de goedheid van de geschiktheid van een model. Men zegt dat een model niet fit is als de p-waarde hoger is dan een vooraf bepaald statistisch significantieniveau, dat idealiter 0,05 is.

De samenvatting geeft ons ook de t-waarde. Hoe hoger de t-waarde, hoe beter het model past.
We kunnen ook de AIC en BIC vinden door de AIC() en de BIC() functies te gebruiken.

AIC(Linear_model)BIC(Linear_model)

Uitvoer

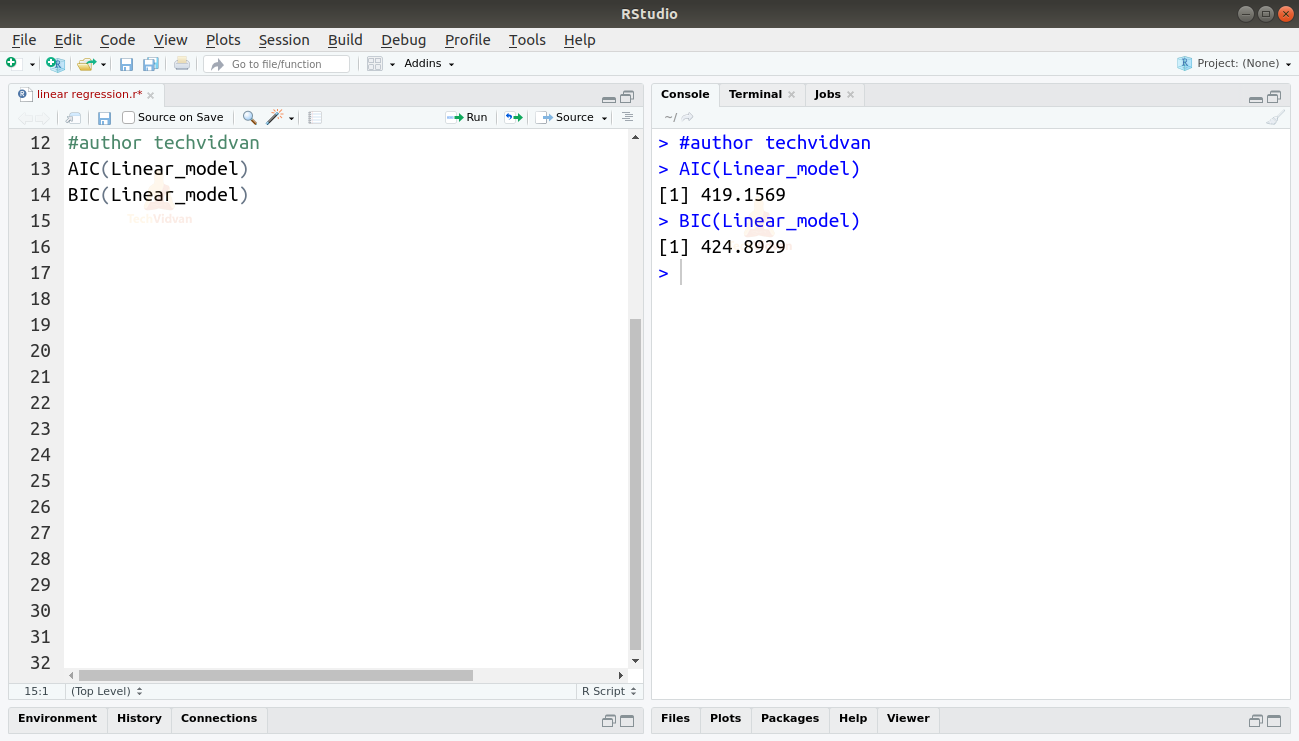
Het model dat resulteert in de laagste AIC en BIC scores heeft de meeste voorkeur.

Samenvatting

In dit hoofdstuk van de TechVidvan’s R tutorial serie, hebben we geleerd over lineaire regressie. We hebben geleerd over eenvoudige lineaire regressie en meervoudige lineaire regressie. Vervolgens bestudeerden we verschillende maatstaven om de kwaliteit of nauwkeurigheid van het model te beoordelen, zoals de R2, aangepaste R2, standaardfout, F-statistiek, AIC, en BIC. Vervolgens hebben we geleerd hoe we lineaire regressie in R kunnen implementeren. Vervolgens hebben we de kwaliteit van de fit van het model in R gecontroleerd.

Deel je beoordeling op Google als je de tutorial Lineaire Regressie leuk vond.