#InsideRL

In een typisch Reinforcement Learning (RL) probleem is er een lerende en een beslisser die agent wordt genoemd en de omgeving waarmee hij interageert wordt omgeving genoemd. De omgeving levert beloningen en een nieuwe toestand op basis van de acties van de agent. Dus, in reinforcement learning, leren we een agent niet hoe hij iets moet doen, maar geven we hem beloningen, positief of negatief, gebaseerd op zijn acties. Onze hoofdvraag voor deze blog is dus hoe we een probleem in RL wiskundig formuleren. Hier komt het Markov Decision Process (MDP) om de hoek kijken.

Voordat we onze hoofdvraag beantwoorden, nl. Hoe we RL problemen wiskundig formuleren (met behulp van MDP), moeten we onze intuïtie ontwikkelen over :

• De relatie Agent-Omgeving
• Markov Eigenschap
• Markov Proces en Markov ketens
• Markov Beloningsproces (MRP)
• Bellman Vergelijking
• Markov Beloningsproces

Grijp je koffie en stop niet tot je trots bent!🧐

De relatie tussen agent en omgeving

Laten we eerst eens kijken naar enkele formele definities :

Agent : Software programma’s die intelligente beslissingen nemen en zij zijn de lerenden in RL. Deze agenten interageren met de omgeving door acties en ontvangen beloningen op basis van hun acties.

Omgeving :Het is de demonstratie van het probleem dat moet worden opgelost.Nu, kunnen we een echte-wereld omgeving of een gesimuleerde omgeving waarmee onze agent zal interageren.

State : Dit is de positie van de agent op een bepaald tijdstip in de omgeving. Telkens wanneer een agent een actie uitvoert, geeft de omgeving de agent een beloning en een nieuwe toestand die de agent heeft bereikt door de actie uit te voeren.

Alles wat de agent niet willekeurig kan veranderen, wordt beschouwd als een deel van de omgeving. Eenvoudig gezegd, acties kunnen elke beslissing zijn die we de agent willen laten leren en toestanden kunnen alles zijn wat nuttig kan zijn bij het kiezen van acties. We gaan er niet van uit dat alles in de omgeving onbekend is voor de agent, bijvoorbeeld de berekening van de beloning wordt beschouwd als een deel van de omgeving, ook al weet de agent een beetje hoe zijn beloning wordt berekend als functie van zijn acties en de toestanden waarin ze worden ondernomen. Dit komt omdat beloningen niet willekeurig door de agent kunnen worden veranderd. Soms is de agent zich volledig bewust van zijn omgeving, maar vindt hij het nog steeds moeilijk om de beloning te maximaliseren, zoals wij misschien weten hoe we Rubik’s kubus moeten spelen, maar hem nog steeds niet kunnen oplossen. We kunnen dus gerust stellen dat de agent-omgeving relatie de grens van de controle van de agent vertegenwoordigt en niet zijn kennis.

The Markov Property

Transition : Het bewegen van de ene toestand naar de andere wordt Transition.

Transition Probability: De waarschijnlijkheid dat de agent van de ene toestand naar de andere gaat, wordt overgangskans genoemd.

De Markov-eigenschap stelt dat :

“De toekomst is onafhankelijk van het verleden gegeven het heden”

Mathematisch kunnen we deze uitspraak uitdrukken als :

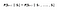
S staat voor de huidige toestand van de agent en s staat voor de volgende toestand. Wat deze vergelijking betekent, is dat de overgang van toestand S naar S volledig onafhankelijk is van het verleden. Dus, de RHS van de vergelijking betekent hetzelfde als LHS als het systeem een Markov-eigenschap heeft. Intuïtief betekent dit dat onze huidige toestand reeds de informatie van de voorbije toestanden bevat.

Staatovergangskans :

Zoals we nu weten wat overgangskansen zijn, kunnen we de staatovergangskans als volgt definiëren :

Voor een Markov-toestand van S naar S, d.w.z. elke andere opvolgende toestand , wordt de kans op toestandsovergang gegeven door

We kunnen de kans op toestandsovergang formuleren in een kansmatrix voor toestandsovergang door :

Iedere rij in de matrix vertegenwoordigt de waarschijnlijkheid dat we van onze oorspronkelijke of begintoestand naar een opvolgende toestand gaan.De som van elke rij is gelijk aan 1.

Markovproces of Markovketen

Markovproces is een willekeurig proces zonder geheugen, d.w.z. een opeenvolging van willekeurige toestanden S,S,….S met een Markov-eigenschap. Het is dus eigenlijk een opeenvolging van toestanden met de Markov-eigenschap. Het kan worden gedefinieerd met behulp van een reeks toestanden (S) en een matrix van de overgangskansen (P).De dynamiek van de omgeving kan volledig worden gedefinieerd met behulp van de staten(S) en de overgangskansmatrix(P).

Maar wat betekent een willekeurig proces ?

Om deze vraag te beantwoorden, bekijken we een voorbeeld:

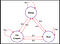
De randen van de boom geven de overgangskansen aan. Laten we uit deze keten een monster nemen. Stel nu dat we sliepen en dat er volgens de kansverdeling een kans van 0,6 is dat we gaan hardlopen en een kans van 0,2 dat we meer gaan slapen en weer een kans van 0,2 dat we een ijsje gaan eten. Op dezelfde manier kunnen we andere reeksen bedenken die we kunnen bemonsteren uit deze keten.

Enkele voorbeelden uit de keten :

• Slaap – Run – IJs – Slaap
• Slaap – IJs – IJs – Run

In de bovenstaande twee reeksen zien we dat we een willekeurige reeks Staten(S) krijgen (d.w.z. Slaap,IJs,Slaap ) elke keer dat we de keten uitvoeren.Hopelijk is het nu duidelijk waarom Markov-processen willekeurige reeksen worden genoemd.

Voordat we naar het Markov-beloningsproces gaan, bekijken we eerst enkele belangrijke concepten die ons zullen helpen bij het begrijpen van MRP’s.

Beloning en rendement

Beloningen zijn de numerieke waarden die de agent ontvangt bij het uitvoeren van een actie in een of andere toestand(en) in de omgeving. De numerieke waarde kan positief of negatief zijn gebaseerd op de acties van de agent.

In Reinforcement learning, geven we om het maximaliseren van de cumulatieve beloning (alle beloningen agent ontvangt van de omgeving) in plaats van, de beloning agent ontvangt van de huidige toestand (ook wel onmiddellijke beloning). Deze totale som van de beloning de agent ontvangt van de omgeving wordt genoemd rendement.

We kunnen opbrengsten definiëren als :

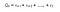
r is de beloning die de agent ontvangt bij tijdstap t tijdens het uitvoeren van een actie(a) om van de ene toestand naar de andere te gaan. Op dezelfde manier is r de beloning die de agent op tijdstip t ontvangt door een actie uit te voeren om naar een andere toestand te gaan. En, r is de beloning die de agent ontvangt bij de laatste tijdstap door een actie uit te voeren om naar een andere toestand te gaan.

Episodische en Continue Taken

Episodische Taken: Dit zijn de taken die een eindtoestand (end state) hebben.We kunnen zeggen dat ze eindige toestanden hebben. Bijvoorbeeld, in race games, we beginnen het spel (start de race) en spelen het tot het spel voorbij is (race eindigt!). Dit wordt een episode genoemd. Zodra we het spel opnieuw starten, begint het vanaf een beginstaat en dus is elke episode onafhankelijk.

Continue Tasks : Dit zijn de taken die geen einde hebben, d.w.z. ze hebben geen eindtoestand. Deze soorten taken zullen nooit eindigen. Bijvoorbeeld leren coderen!

Nu, het is gemakkelijk om het rendement van de episodische taken te berekenen, omdat ze uiteindelijk zullen eindigen, maar hoe zit het met continue taken, omdat het eeuwig door zal gaan. De som van de opbrengsten is oneindig! Dus hoe bepalen we het rendement van doorlopende taken?

Dit is waar we Disconteringsfactor (ɤ) nodig hebben.

Disconteringsfactor (ɤ): Deze bepaalt hoeveel belang moet worden gehecht aan de onmiddellijke beloning en de toekomstige beloningen. Dit helpt ons in feite om oneindigheid als beloning bij doorlopende taken te vermijden. De waarde ligt tussen 0 en 1. Een waarde van 0 betekent dat er meer belang wordt gehecht aan de onmiddellijke beloning en een waarde van 1 betekent dat er meer belang wordt gehecht aan de toekomstige beloningen. In de praktijk zal een discontofactor van 0 nooit leren omdat hij alleen rekening houdt met onmiddellijke beloningen en een discontofactor van 1 zal doorgaan voor toekomstige beloningen, wat tot oneindig kan leiden. Daarom ligt de optimale waarde voor de discontofactor tussen 0,2 en 0,8.

Dus kunnen we het rendement met behulp van de disconteringsfactor als volgt definiëren :(Laten we zeggen dat dit vergelijking 1 is, aangezien we deze vergelijking later gaan gebruiken om de Bellman-vergelijking af te leiden)

Laten we dit aan de hand van een voorbeeld begrijpen,Stel, u woont op een plaats waar u te maken heeft met waterschaarste, dus als iemand naar u toekomt en zegt dat hij u 100 liter water zal geven!(neem aan!) voor de komende 15 uur als een functie van een parameter (ɤ). Laten we eens kijken naar twee mogelijkheden: (Laten we zeggen dat dit vergelijking 1 is, omdat we deze vergelijking later gaan gebruiken om de Bellman-vergelijking af te leiden)

Een met discontofactor (ɤ) 0.8 :

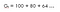
Dit betekent dat we tot het 15e uur moeten wachten omdat de daling niet erg significant is, dus het is nog steeds de moeite waard om tot het einde te gaan. Dit betekent dat we ook geïnteresseerd zijn in toekomstige beloningen.Dus als de discontofactor dicht bij 1 ligt, zullen we moeite doen om tot het einde te gaan omdat de beloning van groot belang is.

Tweede, met discontofactor (ɤ) 0.2 :

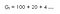
Dit betekent dat we meer geïnteresseerd zijn in vroege beloningen omdat de beloningen om het uur aanzienlijk lager worden.We willen dus misschien niet wachten tot het einde (tot het 15e uur) omdat het dan waardeloos is.Dus, als de kortingsfactor dicht bij nul ligt, zijn onmiddellijke beloningen belangrijker dan toekomstige.

Dus welke waarde van de kortingsfactor moeten we gebruiken?

Het hangt af van de taak waarvoor we een agent willen trainen. Stel, in een schaakspel is het doel de koning van de tegenstander te verslaan. Als we belang hechten aan de onmiddellijke beloningen zoals een beloning bij het verslaan van een pion van een speler van de tegenstander dan zal de agent leren om deze subdoelen uit te voeren ongeacht of zijn spelers ook verslagen worden. Dus, in deze taak zijn toekomstige beloningen belangrijker. In sommige gevallen geven we de voorkeur aan onmiddellijke beloningen, zoals in het watervoorbeeld dat we eerder zagen.

Markov Beloningsproces

Tot nu toe hebben we gezien hoe de Markov-keten de dynamiek van een omgeving definieert met behulp van een verzameling toestanden (S) en een Matrix van de Overgangskansen (P). Maar we weten dat bij het Versterkingsleren alles draait om het doel de beloning te maximaliseren. Dus, laten we beloning toevoegen aan onze Markov-keten. Dit levert ons Markov Beloningsproces op.

Markov Beloningsproces: Zoals de naam al doet vermoeden, zijn MDP’s Markovketens met een waardenoordeel. In principe krijgen we een waarde voor elke toestand waarin onze agent zich bevindt.

Mathematisch definiëren we Markov Reward Process als :

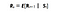
Wat deze vergelijking betekent is hoeveel beloning (Rs) we krijgen van een bepaalde toestand S. Dit vertelt ons de onmiddellijke beloning van die bepaalde toestand waar onze agent zich in bevindt. Zoals we in het volgende verhaal zullen zien, maximaliseren we deze beloningen van elke toestand waarin onze agent zich bevindt. Eenvoudig gezegd, maximaliseren we de cumulatieve beloning die we van elke toestand krijgen.

We definiëren MRP als (S,P,R,ɤ) , waarbij :

• S een verzameling toestanden is,
• P de Overgangswaarschijnlijkheidsmatrix is,
• R de Beloningsfunctie is , die we eerder zagen,
• ɤ de discontofactor is

Markov Beslissingsproces

Nu, laten we onze intuïtie voor Bellman Vergelijking en Markov Beslissingsproces ontwikkelen.

Beleidsfunctie en waardefunctie

De waardefunctie bepaalt hoe goed het voor de agent is om in een bepaalde toestand te zijn. Natuurlijk, om te bepalen hoe goed het zal zijn om in een bepaalde staat te zijn moet het afhangen van sommige acties die het zal nemen. Dit is waar het beleid om de hoek komt kijken. Een beleid bepaalt welke acties in een bepaalde toestand s.

Een beleid is een eenvoudige functie, die een waarschijnlijkheidsverdeling over Acties (a∈ A) voor elke toestand (s ∈ S) definieert. Als een agent op tijdstip t een beleid π volgt dan is π(a|s) de waarschijnlijkheid dat agent met het nemen van actie (a ) op bepaalde tijdstap (t). In Reinforcement Learning bepaalt de ervaring van de agent de verandering in beleid. Wiskundig wordt een beleid als volgt gedefinieerd :

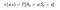
Nu, hoe vinden we een waarde van een toestand.De waarde van toestand s, wanneer de agent een beleid π volgt dat wordt aangeduid met vπ(s), is het verwachte rendement vanaf s en het volgen van een beleid π voor de volgende toestanden, totdat we de eindtoestand bereiken.We kunnen dit formuleren als :(Deze functie wordt ook wel State-value Function genoemd)

Deze vergelijking geeft ons de verwachte opbrengsten beginnend bij toestand(s) en gaande naar de opvolgende toestanden daarna, met het beleid π. Het rendement dat we krijgen is stochastisch, terwijl de waarde van een toestand niet stochastisch is. Het is de verwachting van het rendement van starttoestand s en daarna, naar elke andere toestand. Merk ook op dat de waarde van de eindtoestand (als die er is) nul is. Laten we eens naar een voorbeeld kijken :

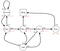
Stel dat onze begintoestand Klasse 2 is, en we gaan naar Klasse 3 dan Pass en dan Sleep.Kortom, Klasse 2 > Klasse 3 > Pass > Sleep.

Onze verwachte opbrengst is met discontofactor 0,5:

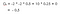
Note:Het is -2 + (-2 * 0.5) + 10 * 0.25 + 0 in plaats van -2 * -2 * 0.5 + 10 * 0.25 + 0.Dan is de waarde van Klasse 2 -0.5 .

Bellmanvergelijking voor waardefunctie

Bellmanvergelijking helpt ons om optimaal beleid en waardefunctie te vinden.We weten dat ons beleid verandert met ervaring, dus we zullen verschillende waardefuncties hebben volgens verschillende beleidslijnen.Optimale waardefunctie is er een die maximale waarde geeft in vergelijking met alle andere waardefuncties.

Bellmanvergelijking stelt dat de waardefunctie in twee delen kan worden ontleed:

• Immediate Reward, R
• Discounted value of successor states,

Mathematisch kunnen we Bellmanvergelijking definiëren als :

Laten we aan de hand van een voorbeeld eens begrijpen wat deze vergelijking zegt :

Voorstel, er is een robot in een bepaalde toestand (s) en dan beweegt hij van deze toestand naar een andere toestand (s’). De vraag is nu hoe goed het voor de robot was om in de toestand (s) te zijn. Met behulp van de Bellman-vergelijking kunnen we zeggen dat dit de verwachte beloning is die hij kreeg bij het verlaten van de toestand(en) plus de waarde van de toestand (s’) waarnaar hij bewoog.

Laten we eens kijken naar een ander voorbeeld :

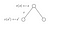
We willen de waarde van toestand s weten.De waarde van toestand(en) is de beloning die we hebben gekregen bij het verlaten van die toestand, plus de contante waarde van de toestand waarin we terecht zijn gekomen, vermenigvuldigd met de overgangskans dat we ernaartoe zullen gaan.

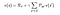
De bovenstaande vergelijking kan in matrixvorm als volgt worden uitgedrukt :

Waarbij v de waarde is van de toestand waarin we ons bevonden, die gelijk is aan de onmiddellijke beloning plus de verdisconteerde waarde van de volgende toestand, vermenigvuldigd met de waarschijnlijkheid om naar die toestand te gaan.

De complexiteit van de looptijd van deze berekening is O(n³). Daarom is dit duidelijk geen praktische oplossing voor het oplossen van grotere MRP’s (hetzelfde geldt voor MDP’s). In latere Blogs zullen we kijken naar efficiëntere methoden, zoals Dynamisch Programmeren (waarde iteratie en beleids iteratie), Monte-Claro methoden en TD-Learning.

We gaan het in het volgende verhaal veel gedetailleerder hebben over de Bellman-vergelijking.

Wat is Markov Beslissingsproces ?

Markov Beslissingsproces : Het is een Markov Beloningsproces met een beslissingen.Alles is hetzelfde als MRP, maar nu hebben we een agentschap dat beslissingen neemt of acties onderneemt.

Het is een tupel van (S, A, P, R, 𝛾) waarin:

• S is een verzameling toestanden,
• A is de verzameling acties die de agent kan kiezen om te ondernemen,
• P is de overgangskansmatrix,
• R is de Beloning die door de acties van de agent wordt geaccumuleerd,
• 𝛾 is de discontofactor.

P en R veranderen lichtjes naargelang de acties als volgt :

Transition Probability Matrix

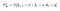
Reward Function

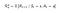
Nu is onze beloningsfunctie afhankelijk van de actie.

Tot nu toe hebben we het gehad over het krijgen van een beloning (r) wanneer onze agent een reeks toestanden (s) doorloopt volgens een beleid π.In feite is het beleid in een Markov Beslissingsproces (MDP) het mechanisme om beslissingen te nemen. We hebben nu dus een mechanisme dat ervoor kiest om een actie te ondernemen.

Beleid in een MDP is afhankelijk van de huidige toestand. Het is niet afhankelijk van de geschiedenis. Dat is de Markov-eigenschap. Dus de huidige toestand waarin we ons bevinden, karakteriseert de geschiedenis.

We hebben al gezien hoe goed het voor de agent is om in een bepaalde toestand te zijn (State-value function).Laten we nu eens kijken hoe goed het is om een bepaalde actie te ondernemen volgens een beleid π vanuit toestand s (Action-Value Function).

State-action value function of Q-Function

Deze functie specificeert de hoe goed het voor de agent is om actie (a) te ondernemen in een toestand (s) met een beleid π.

Mathematisch kunnen we de State-action value function definiëren als :

Basically, het vertelt ons de waarde van het uitvoeren van een bepaalde actie (a) in een staat (s) met een beleid π.

Laten we eens kijken naar een voorbeeld van een Markov Beslissingsproces :

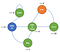
Nu kunnen we zien dat er geen waarschijnlijkheden meer zijn.In feite heeft onze agent nu keuzes te maken, zoals na het wakker worden, kunnen we kiezen om netflix te kijken of te coderen en debuggen. Natuurlijk zijn de acties van de agent gedefinieerd w.r.t. een beleid π en zal de beloning dienovereenkomstig krijgen.