Je weet misschien dat om een vergelijking van graad 2 op te lossen, ax²+bx+c = 0, we de kwadratische formule gebruiken.

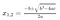
Er bestaan soortgelijke formules voor vergelijkingen van graad 3 en 4, maar ze ontbreken op mysterieuze wijze voor 5 of hoger. Meer specifiek lijkt het erop dat we de oplossingen van de quintica (vergelijking van graad 5) of hoger niet kunnen construeren met alleen optellen, aftrekken, vermenigvuldigen, delen, en radikalen (vierkantswortels, derdemachtswortels, enz.). Waarom is dat, wat is er zo speciaal aan het getal 5? Dit waren vragen die de jonge Fransman Evariste Galois begin 1800 achtervolgden, en de nacht voordat hij dodelijk gewond raakte in een duel, schreef hij een theorie op van een nieuw wiskundig object, een “groep” genaamd, dat het probleem op een verrassend elegante manier oplost.

Zo deed hij het.

De verzameling wortels van verschillende vergelijkingen zijn van verschillende complexiteit. Sommige verzamelingen zijn zo complex dat ze niet kunnen worden uitgedrukt met alleen eenvoudige objecten zoals radikalen. Maar hoe meten we de complexiteit van de wortels als we ze niet eens kunnen berekenen, en welke maatstaf voor complexiteit moeten we gebruiken?

Permuterende wortels en symmetrie

Het antwoord ligt in de symmetrie van de wortels.

Symmetrie van de wortels zult u zich misschien afvragen, wat heeft dat er nou mee te maken? Wat betekent het zelfs?

Laten we de wortels van twee vergelijkingen plotten en kijken of we er iets zinnigs over kunnen zeggen:

Van de linker wordt gezegd dat hij minder symmetrisch is dan de rechter. Dit kan u verbazen, want in de spreektaal wordt symmetrisch meestal gebruikt als men het voorwerp kan spiegelen of draaien zonder dat het uiterlijk verandert. In die zin ziet het linker plaatje er symmetrischer uit.

Voorbeeld: De ster is symmetrischer dan het hart, omdat men het behalve kan spiegelen ook kan roteren.

Maar in ons geval gaan we een algemenere kijk op symmetrieën hanteren. We beperken ons niet tot reflecties en rotaties, elke functie die het object transformeert zonder het er anders uit te laten zien, komt in aanmerking. In het geval van de wortels betekent dit dat elke functie die de wortels op een of andere manier verwisselt (permuteert) geldig is. Meer functies betekent symmetrischer.

Het blijkt dat er in het rechter geval functies zijn om alle wortels in elke denkbare volgorde te permuteren, maar liefst 5!=120, dus het is zeer symmetrisch. Maar in het linkse geval, als we r₂↔r₄ verwisselen met behulp van de transformatie i↔-i, verwisselen we noodzakelijkerwijs ook r₁↔r₅. Dit beperkt ons, en dus zijn niet alle denkbare permutaties mogelijk. Het is minder symmetrisch.

De functies die de wortels permuteren heten “automorfismen”, en als we die automorfismen groeperen krijgen we wat men een “Groep” noemt (op betere definities van automorfismen en groepen kom ik later terug).

Dit betekent dat de groep die de symmetrieën van de wortels weergeeft groter en complexer is in het rechter geval. In feite is de groep in het rechter geval zo complex dat de wortels niet met radicalen kunnen worden beschreven.

Hoe weten we hoe complex een groep is? Om dit te begrijpen hebben we wat meer theorie nodig.

De grootte van de quintische

Laten we eerst eens kijken naar de grootte van een groep. Hoe weet ik dat er kwinten zijn die een 5! grote groep hebben?

Een algemene quintica ziet er normaal gesproken zo uit:

x⁵+ax⁴+bx³+cx²+dx+e=0

Maar als we een meer “wortel-centrische” benadering kiezen, kunnen we zeggen dat hij er zo uitziet:

(x-r₁)(x-r₂)(x-r₃)(x-r₄)(x-r₅)=
x⁵-(r₁+r₂+r₃+r₄+r₅)x⁴+
(r₁r₂+r₁r₃+r₁r₄+r₂r₄+r₃r₄+r₁r₅+r₂r₅+r₃r₅+r₄r₅)x³…- r₁r₂r₃r₄r₅=0

Dat wil zeggen dat de constante a,b,c,d,e in de eerste vergelijking vervangen wordt door een symmetrische combinatie van de wortels:

r₁+r₂+r₃+r₄+r₅=a
r₁r₂+r₁r₃+r₁r₄+r₂r₄+r₃r₄+r₁r₅+r₂r₅+r₃r₅+r₄r₅=b
(c en d kortheidshalve weggelaten)
r₁r₂r₃r₄r₅ = e

Als je alle termen in detail bekijkt, ontdekt men dat het verwisselen van de wortels geen invloed heeft op de vergelijking (probeer het bijvoorbeeld voor b hierboven). Dit geldt voor veeltermen van elke graad. Omdat we alle wortels kunnen verwisselen, kunnen we concluderen dat de symmetriegroep van deze algemene kwintische in feite alle permutaties is, ook wel S₅ genoemd (de symmetrische groep van orde 5).

Velden en automorfismen

Nu gaan we onze definitie van automorfismen wat uitbreiden, want ze zijn meer dan alleen functies die wortels permuteren. In het proces moeten we iets introduceren dat “velden” heet. Waarom zouden we dat willen doen, zegt u? De reden is, dat terwijl het werken met wortels en hun permutaties leuk is, het een beetje gemakkelijker is om te werken met velden en hun automorfismen. Het zijn precies dezelfde functies, maak je geen zorgen, alleen een andere manier om ze te bekijken.

Dus, als de vergelijking is, zeg x²-2=0, in plaats van te werken met de wortels, r₁=√2, r₂=-√2 gaan we het veld Q(√2) introduceren. Dit zijn alle rationale getallen Q met een toegevoegde √2. √2 wordt een “velduitbreiding” genoemd. Het ziet er zo uit: a+b√2 a,b∈Q. Om de wortel van de vergelijking te kunnen beschrijven hebben we het veld Q(√2) nodig. Voor elke veldextensie (en ook andere wiskundige objecten) hebben we een stel functies, σₙ, die een getal naar een ander uniek getal in hetzelfde veld stuurt en de voorwaarde σ(a+b)=σ(a)+σ(b) en σ(ab)=σ(a)σ(b) volgt. σ is een functie van de extensie en raakt niet aan het onderliggende veld Q. Deze functies worden automorfismen genoemd. Overigens permuteren zij ook de wortels. Dit komt omdat voor de wortel r:

r⁵+ar⁴+br³+cr²+dr+e=0⟹
σ(r⁵+ar⁴+br³+cr²+dr+e)=σ(0)⟹
σ(r)⁵+aσ(r)⁴+bσ(r)³+cσ(r)²+dσ(r)+e=0 (omdat σ niet aan Q raakt (waar a, b, c, d,e leven))

Dit betekent dat σ(r) ook een oplossing van de vergelijking is. En omdat:

σ(r₁)-σ(r₂)=σ(r₁)+σ(-1)σ(r₂)=σ(r₁-r₂)≠0

zijn de wortels verschillend, dus hebben we er 5, en dat moeten de oorspronkelijke 5 zijn. Dus σ moet de wortels permuteren.

Natuurlijk werkt dit voor een vergelijking van elke graad.

Hieruit volgt:

1. We hebben onze vergelijking.
2. Die vergelijking heeft een veld dat een uitbreiding van een paar radicalen kan bevatten
3. Die velduitbreiding heeft een groep, die een verzameling is van al zijn automorfismen.

Twee voorbeelden van graad 3

Vraagstelling: x³-x²-2x+2=0

De wortels zijn (1,√2,-√2) (je kunt dit zelf nagaan door ze in te vullen), dus het veld moet Q(√2)

Alle manieren opschrijven die we kunnen bedenken om de wortels te permuteren (e betekent identiteitspermutatie, het doet niets):

(e)
(√2↔-√2)
(1↔-√2)
(1↔-√2)
(√2→-√2 en 1→√2)
(√2↔-√2 en 1↔-√2)

Laten we er een uitproberen: Laat (√2↔-√2) σ₁ zijn:

σ₁(√2+-√2)=σ₁(0)=0=σ₁(√2)+σ₁(-√2)
σ₁((√2)(-√2))=σ₁(-2)=-2=σ₁(√2)σ₁(-√2)

Zo ver is alles goed. Nog eentje.

Laat (1↔√2) σ₂ zijn:

σ₂(√2+-√2)=σ₂(0)=0 ≠ σ₂(√2)+σ₂(-√2)=1+-√2
σ₂((√2)(-√2))=2 ≠ σ₂(√2)σ₂(-√2)=1(-√2)

Het is duidelijk dat σ₂ geen automorfisme is, dus die zullen we moeten schrappen. De andere σ stuit op soortgelijke problemen, de enige die overblijven zijn e en σ₁. Dit noemen we de cyclische groep C₂, omdat we alleen in een cirkel kunnen permuteren (een heel kleine cirkel in dit geval).

Voorbeeld 2

Vraagstelling: x³-2=0

De wortels zijn

dus moet het veld

waarbij we kortheidshalve ζ gebruiken. Zo ziet het eruit:

Men kan een beetje spelen met de wortelpermutaties, en zal al snel merken dat het in dit geval allemaal automorphismen zijn. Er zijn dus 3! automorfismen, en dat zijn alle wortelpermutaties, dus de groep moet S₃ zijn.

Een ander leuk ding om op te merken over het plaatje hierboven is dat het eruit ziet als een gelijkzijdige driehoek en dat de automorfismen precies overeenkomen met het roteren en spiegelen van de driehoek. Als de automorfismen op deze manier overeenkomen met de symmetrieën van een regelmatige veelhoek, heet de groep een “Dihedraalgroep”. In dit geval D₃. Gewoonlijk is de groep van alle permutaties Sₙ niet dezelfde als de tweevlaksgroep Dₙ, maar in het geval van n=3 wel.

Groepen

Dit lijkt me een goede plaats om in te gaan op een wat langere discussie over groepen. Groepen zijn begonnen als verzamelingen van permutaties van wortels, maar kunnen ook gezien worden als verzamelingen van automorfismen, of rotaties en spiegelingen van symmetrische meetkundige objecten. Elke verzameling van functies die een voorwerp zo verandert dat het er hetzelfde uitziet, kan als een groep worden beschouwd. Maar we kunnen ook naar de transformaties zelf kijken zonder ons te bekommeren om het symmetrisch object waarop ze werken. Net zoals we ons bij het rekenen niet druk maken over stapels appels, maar gewoon de regels volgen, zo kunnen we ook enkele regels opstellen die de transformaties van een groep volgen, en die gebruiken.

De regels zijn ongeveer als volgt:

Als we eerst een transformatie doen, en dan nog een, dan krijgen we een derde transformatie die nog steeds in de groep zit. Bijvoorbeeld, de groep C₄ is de groep van alle rotaties die men op een vierkant kan doen. Als a 90∘ roteert, b 180∘ roteert en c 270∘ roteert, dan is a∗b=c. Waarbij ∗ betekent, doe eerst b dan a, meestal vermenigvuldiging genoemd omdat het (een beetje) lijkt op vermenigvuldiging van getallen. Volgens de bovenstaande regel moet c in de groep zitten. Dit heet sluiting.

Er moet een identiteitselement (e) zijn dat helemaal niets doet.

Voor elk element moet er een omgekeerde van dat element zijn.

Nu kunnen we de eigenschappen van verschillende groepen onderzoeken zonder ons zorgen te hoeven maken over wortels of veelhoeken.

Visualiseren van groepen

Twee leuke manieren om groepen te visualiseren zijn:

Cayley-tabellen

Het bovenstaande is de Caylay-tabel voor een gelijkzijdige driehoek, de D₃-groep. Het zijn alle elementen van de groep en welke elementen we krijgen als we ze vermenigvuldigen. Bijvoorbeeld, als we eerst een 120∘ rotatie (r) doen en dan nog eens dezelfde rotatie, dan krijgen we een 240∘ rotatie rr=r² zoals te zien is in de tabel. Als we een 120∘ rotatie-flip rf en een r doen krijgen we enkel een flip. Merk op dat de elementen f en r niet paren. Een groep waarvan de elementen paren heet een abeliaanse groep.

Deze tabel is echter nog steeds zeer symmetrisch, maar dat hoeft niet zo te zijn. Elk door elkaar husselen van de elementen die de regels volgen is geldig.

Caylay-grafiek

Het bovenstaande is de D₃ Caylay-grafiek. Hier zijn de elementen weergegeven op een manier om te laten zien hoe je van het ene element naar het volgende komt, waarbij de randen de bewerkingen zijn. In dit geval is een 120∘ rotatie en een spiegeling nodig, deze (r en f) worden ook wel de generatoren van de groep genoemd, omdat men daarmee de hele groep kan genereren, uitgaande van het identiteitselement.

Gebruik van groepen

Groepen hebben de neiging overal nuttig te zijn waar symmetrie aanwezig is. Zo worden de behanggroepen gebruikt om symmetrische behangsoorten te beschrijven. Er zijn behangsoorten die 180∘ gedraaid kunnen worden en er zijn behangsoorten die gespiegeld kunnen worden en er zijn behangsoorten die beide kunnen, enzovoort. Het blijkt dat er slechts 17 van hen, dus het is een nette manier van classificatie wallpapers.

De bovenstaande wallpapers behoren beide tot een groep genaamd p6m.

Een andere, meer verrassende, toepassing van groepen is in de natuurkunde. Het lijkt alsof de natuurwetten bepaalde symmetrieën volgen. Bijvoorbeeld, als men Newtons tweede wet F=ma transformeert, is hij 10 minuten in de toekomst nog steeds dezelfde. Dat de natuurwetten niet veranderen van de ene dag op de andere lijkt erop te wijzen dat zij symmetrisch zijn met betrekking tot tijd-transformatie. Zij veranderen ook niet van de ene plaats naar de andere, dus zijn transformaties in de ruimte ook toegestaan. Aangezien het mogelijk is tijd en ruimte in willekeurig kleine of grote brokken te transformeren bevatten de groepen die deze beschrijven, Lie-groepen, een oneindig aantal elementen.

Intrigerend is dat blijkt dat deze symmetrieën alle te maken hebben met een behoudswet. Tijdsymmetrie brengt behoud van energie met zich mee, ruimtesymmetrie behoud van impulsmoment, hoeksymmetrie (de natuur ziet er vanuit alle hoeken hetzelfde uit) behoud van impulsmoment enzovoort. Emmy Noether toonde dit aan door de symmetrieën te combineren met het principe van de minste actie, een natuurwet die stelt dat de natuur de neiging heeft “de kortste weg te nemen”.

Ik vind het interessant hoeveel van alle complexiteit en schijnbare chaos in de natuur verklaard kan worden door zulke intuïtieve begrippen als “natuurwetten veranderen niet van dag tot dag” en “de natuur heeft de neiging de kortste weg te nemen”.

Terug naar velden

Einde van het intermezzo, waar waren we gebleven? Juist, we hadden het over x³-3=0 en zijn wortels en velden.

Het veld van die vergelijking is Q(³√2, ζ) en het zou natuurlijk zijn te denken dat het er zo uitziet: a+b³√2+cζ, maar dat is onjuist. De reden hiervoor is dat we willen dat ons veld “gesloten” is. Dat wil zeggen dat als we twee elementen in het veld optellen of vermenigvuldigen we willen dat ze in het veld blijven. Dus bijvoorbeeld ³√2 en ζ staan beide in bovenstaand veld maar ³√2ζ niet.

Subvelden en subgroepen

Kijken we naar onze voorbeelden van graad 3 hierboven dan hebben we

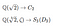
Het lijkt erop dat het tweede veld en de tweede groep complexer zijn dan het eerste veld en de eerste groep. We kunnen dit raden door gewoon het aantal termen te tellen in het veldgeval of het aantal automorfismen in het groepgeval. Maar alleen tellen lijkt niet echt weer te geven wat het betekent om complex te zijn. Neem bijvoorbeeld de groep C₁₂. Veel elementen, maar het roteert alleen de wortels, dus lijkt het niet zo complex. Een overeenkomstig veld is Q(e^π/6). Het zal e^π/6,e^2π/6 bevatten… maar ook weer niet erg complex.

Hoe complex een groep is, zal de sleutel zijn om te begrijpen waarom sommige wortels niet beschreven kunnen worden door alleen radikalen, onthoud dat.

Om de complexiteit beter te kunnen waarderen gaan we het begrip “Subveld” en “Subgroep” introduceren. Een subveld is wanneer je enkele termen weghaalt, maar je hebt nog steeds een gesloten veld. Evenzo is er sprake van een subgroep wanneer men enkele automorfismen verwijdert maar nog steeds een gesloten groep heeft.

In het eerste geval Q(√2) kan men alleen de √2 in het veld en een van de twee automorfismen in de groep verwijderen (men kan niet (e) verwijderen en toch een groep hebben).

In het tweede geval Q(³√2, ζ) wordt het wat ingewikkelder. Men kan handmatig de deelvelden/groepen destilleren door gewoon elementen één voor één te verwijderen en te kijken of het resulterende veld/de resulterende groep gesloten is. Na een tijdje komen we op het volgende uit:

Opvallend is dat zowel het veld als de groep vier bestanddelen hebben. Nu zou het een redelijke veronderstelling zijn dat de deelgroepen altijd precies de automorfismen van de deelvelden bevatten. Maar dat is niet zo.

Vaste velden

Geluk niet, we zijn er bijna, het is alleen nog een klein beetje ingewikkelder. Om dit te zien, laten we eens kijken naar het veld Q(⁴√2, i) en zijn subvelden.

Het veld Q(⁴√2, i) heeft de permutatie-groep D₄ (hetzelfde als een vierkant). Laten we eens kijken naar D₄ en zijn ondergroepen.

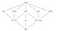
Het subgroepenrooster staat op zijn kop in dit plaatje met D₄ onderaan, daar kom ik zo op, maar laten we eerst eens kijken naar de subvelden contra de subgroepen. Q(⁴√2, i) heeft 5 grote subvelden en 3 kleine sub-subvelden, maar D₄ heeft slechts 3 grote subgroepen en 5 kleinere sub-subgroepen.

Het lijkt erop dat er niet genoeg grote groepen zijn om de 5 grote velden te permuteren. Als je met de subgroepen en subvelden zou spelen, zou je uiteindelijk tot de conclusie komen dat de subgroepen in feite niet de subvelden permuteren, maar alles wat niet in de subvelden staat, dat zij de subvelden “repareren” of niet raken.

Dus bijvoorbeeld (f) fixeert Q(⁴√2) en (r², f) fixeert Q(√2).

Waarom is het zo en niet andersom, zoals we eerst dachten?

Ik heb geen intuïtieve manier om dit uit te leggen, de manier waarop ik het zie is dat we het empirisch hebben ontdekt en nu kunnen we proberen het te bewijzen. Het bewijs gaat ongeveer zo:

Handige fundamentele stelling van de Galoistheorie bewijsschets

We willen laten zien dat als we het subgroeprooster omdraaien we een één-op-één correspondentie krijgen met het subveldrooster waarbij de velden de vaste velden van de groepen zijn.

Eerst wil ik erop wijzen dat het redelijk (soort van) is dat dit het geval is. Bij de onderste groep hebben we alle automorfismen, die natuurlijk om alles heen bewegen behalve om Q (fixeert Q), en bij de bovenste groep hebben we alleen het e-automorfisme, dat om niets heen beweegt (fixeert alles).

Als we bij de onderste groep beginnen en een paar automorfismen verwijderen, dan zullen de verwijderde automorfismen niet meer om een klein deel van het veld heen bewegen en dus dat deel van het veld fixeren. Naarmate we meer automorfismen verwijderen, zal een steeds groter deel van het veld onaangetast blijven en krijgen we dus een groter gefixeerd veld.

Om wat rigoureuzer te zijn, moeten we de grootte van de groep en het veld kunnen vergelijken. De grootte van de groep is natuurlijk het aantal automorphismen in de groep. De grootte van het veld is het aantal termen. Deze twee zijn toevallig gelijk, maar waarom is dat zo?

Quotient

Nu zouden we kunnen kijken naar het S₅ deelgroepenrooster van de quintische en zien dat het er inderdaad behoorlijk complex uitziet. Maar om dit te kunnen verbinden met radicalen hebben we een manier nodig om de complexiteit tussen groepen en hun ondergroepen te analyseren. Dat wil zeggen: Hoeveel complexer is D₄ dan bijvoorbeeld C₄? Om dit te doen introduceren we het concept van een “quotiënt”. Een quotiënt is eigenlijk groepsdeling. Hoe werkt dat?

In een gewone deling doen we zoiets als dit: Om 15 appels te verdelen over 5 personen, groeperen we de appels in de appelset in 5 gelijke stapels en elke stapel komt overeen met een persoon in de persoonsset. Het antwoord op de vraag 15/5 is 3, een van de stapels, elke stapel is goed omdat ze gelijk zijn.

Een soortgelijk iets gebeurt als we groepen verdelen. Om D₄ te delen door C₄ groeperen we de 8 elementen van D₄ in 4 gelijke groepen, één voor elk element in C₄. Hoe maken we de groepen gelijk? Het is niet zo dat de elementen allemaal identieke appels zijn. Het kunnen bijvoorbeeld heel verschillende automorphismen zijn. Wel, quotiënten zijn om precies die reden niet altijd mogelijk. Maar soms kan een groep verdeeld worden in “Cosets”. Stel dat we D₄ verdelen in 4 gelijke delen met 2 elementen in elk. Als we geluk hebben kunnen we 4 stapels van elementen hebben waarbij de verhouding tussen de twee elementen in alle stapels gelijk is. Om dit te kunnen doen moet de oorspronkelijke groep een hoge mate van zelfgelijkenis vertonen. Om dit te zien, laten we eens kijken naar een Cayley-grafiek van D₄.

Zoals men kan zien is er hier in feite een hoge mate van zelfgelijkenis. De linkerboven-, rechterboven-, linkeronder- en rechterbenedenhoek zien er allemaal hetzelfde uit. Dit zijn onze cosets.

Dus D₄/C₄ is in feite een van deze cosets, en dat is C₂. Dus: D₄/C₄=C₂.

Nu, door de introductie van quotiënten hebben we eigenlijk een concept van hoe je groepen van de grond af aan opbouwt. Net zoals 21 bestaat uit 3 en 7, zo bestaan groepen uit hun ondergroepen. En net zoals we de bestanddelen van een getal kunnen krijgen door te delen, 21/7=3, zo kunnen we de bestanddelen van een groep krijgen door het quotiënt te nemen. Aangezien D₄/C₄=C₂, betekent dit dat als we een C₄ groep hebben, we die moeten vermenigvuldigen met C₂ om tot D₄ te komen. Aangezien er een overeenkomst is tussen velden en groepen, zal dit een rol spelen in hoe we velden construeren.

Radicalen

Subgroepen van de quintische

Nu, Ik zal geen plaatje laten zien van het groepsrooster van S₅ omdat het te groot is, maar ik zal wel een paar dingen zeggen over de ondergroepen. Een van de ondergroepen is A₅ (Alternatieve groep) die gemakkelijk te controleren is. Om van A₅ naar S₅ te komen moeten we S₅/A₅=C₂. We kunnen er dus komen via radicalen, maar: Een ondergroep van A₅ is (e), maar A₅/e is geen cyclische groep. Dit geldt trouwens voor elke An met n≥5. We kunnen er dus niet komen met radicalen en helaas, elke polynoom van graad ≥5 kan niet worden opgelost met radicalen.

En zo vond Galois, als tiener, het begrip groep uit om een al lang bestaande open vraag over de onoplosbaarheid van de kwintische⁹ te bewijzen.

Trisecteren van de hoek

Een leuk bonusfeit dat we krijgen van de machinerie rond Galois theorie, in dit geval de torenwet voor velden, is een mooi bewijs van een probleem dat de mensheid al sinds de oude Grieken voor een raadsel stelt, namelijk: De onmogelijkheid om een hoek in drieën te delen met een liniaal en een passer. Blijkbaar hielden de Grieken ervan om dingen op deze manier te tekenen en waren ze nieuwsgierig naar de beperkingen van de methode.

Een voorbeeld is het vinden van een punt in het midden van twee andere punten. Zet daartoe de passer op de twee punten en teken eerst een cirkel om het ene en dan om het andere. Gebruik de liniaal als liniaal en trek een lijn tussen de punten en vervolgens tussen de punten waar de cirkels elkaar kruisen. Het midden is waar de lijnen elkaar kruisen.

Maar hoe vertaalt zich deze manier van tekenen naar de veldtheorie? Welnu, men kan bovenstaand probleem zien als, stel we hebben een veld van twee punten, (x₁,y₁) en (x₂,y₂). We willen het veld uitbreiden zodat het ook het middelste punt bevat. Daartoe vinden we de snijpunten van de cirkels (x-x₁)²+(y-y₁)²=r en (x-x₂)²+(y-y₂)²=r. We krijgen twee nieuwe punten (x₃, y₃) en (x₄,y₄). De lijn tussen deze punten is y=(y₄-y₃)/(x₄-x₃)x. De lijn tussen de eerste twee punten is y=(y₂-y₁)/(x₂-x₁)x. Los op voor x om te krijgen waar ze elkaar kruisen.

Het is duidelijk dat de constructies van passer en liniaal neerkomen op het oplossen van vergelijkingen van graad een en twee.

Maar wat komt het trisecteren van een hoek dan neer op het oplossen van vergelijkingen van graad een en twee?

De driehoeksformule levert op:

Maar aangezien het gebruik van een liniaal en passer hetzelfde was als het oplossen van één- en tweedimensionale vergelijkingen zijn de enige mogelijke velduitbreidingen 2 voor één bewerking, en dan kunnen we met de nieuwe punten tot machten van 2 komen: 4,8,16 etc maar nooit 3.

Hoewel het onmogelijk is de hoek te trisecteren met behulp van alleen een passer en een liniaal, is het wel mogelijk met behulp van origami.

Oplossen van de algemene quintica

Het moet gezegd worden dat, hoewel de algemene quintica niet met radicalen kan worden opgelost, dit wel kan met de “Jacobi theta functie”.

1. Galois Theorie voor Beginners: Een Historisch Perspectief. Jörg Bewersdorff
2. http://pi.math.cornell.edu/~kbro…
3. Field Automorphisms
4. https://kconrad.math.uconn.edu/b…
5. https://faculty.math.illinois.ed…
6. Wolfram|Alpha: De kennis van de wereld berekenbaar maken
7. https://www.wikiwand.com/en/Galois_theory
8. https://www.wikiwand.com/en/%C3%89variste_Galois
9. https://www.youtube.com/watch?v=8qkfW35AqrQ&list=PLwV-9DG53NDxU337smpTwm6sef4x-SCLv&index=36