Learning Objectives
- 独占的競争者が限界収入と限界費用を用いて価格と量を選択する方法を説明しなさい
- 独占的競争企業の平均、限界費用をグラフにして解釈しなさい
。 需要曲線と平均費用曲線を用いて、独占的競争相手の総収入、利益、損失を計算する
利益最大化生産量と価格の選択
独占的競争企業は独占企業とほぼ同じ方法で利益最大化量と価格を決定している。
利潤最大化の独占的競争相手の例として、チーズ、甘酢ソース、野菜と肉を選べるピザを出す本格中華ピザ屋を考えてみよう。 オーセンティック・チャイニーズ・ピザは、他のピザ・ビジネスやレストランと競争しなければならないが、差別化された製品を持っている。 図1および表1の最初の2列に示すように、この会社の需要曲線は下向きに傾斜している。
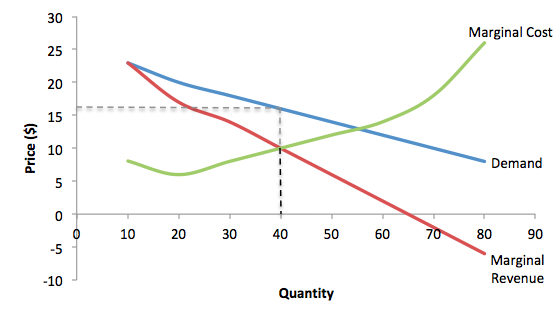
図1. 独占的な競争相手が利益を最大化する生産量と価格を選択する方法。 利潤を最大化するために、本格中華ピザ店は限界収入が限界費用に等しくなる数量、つまりMR=MCとなるQを選択することになる。 ここでは,数量は40,価格は16ドルを選択することになる。 収益と費用のスケジュール
となる。
需要曲線の各点における価格と数量の組み合わせを掛け合わせると、会社が受け取るであろう総収入が計算でき、それは表1の3列目に示すとおりである。 第4列の限界収益は、総収益の変化を数量の変化で割ったものである。 表1の最後の列は、総費用、限界費用、平均費用である。 いつものように、限界費用は総費用の変化を数量の変化で割ったものであり、平均費用は総費用を数量で割ったものである。 次の例は、これらの企業がどのような価格でどれだけ自社製品を供給するかを計算する方法を示している。
How a Monopolistic Competitor Determines How Much to Produce and at What Price
The process by which a monopolistic competitor choises its profit-maximizing quantity and price similarly how a monopoly makes these decisions process.専売企業が利益最大化量と価格を選択した過程は、専売企業がこれらの決定過程を行う方法に酷似している。 まず,企業は生産する利潤最大化量を選択する。 次に、企業はその数量に対してどのような価格を課すかを決定する。
ステップ1。 独占的競争者は、その利潤最大化生産水準を決定する。 この場合、本格中華ピザの会社は、限界収入と限界費用を考慮して生産する利益最大化数量を決定する。 2つのシナリオが考えられる:
- 限界収入が限界費用を上回る生産量で生産している場合、各限界単位が費用以上の収入をもたらすことによって利益を増やしているので、会社は生産を拡大し続けるべきである。 このように、会社はMR=MC.
- 会社が限界費用が限界収入を上回る量で生産している場合、各限界単位はそれがもたらす収入よりも費用がかかっており、会社はMR=MCまで生産量を減らすことによって利益を増加させることになる。
この例では、MRとMCは40の数量で交差し、これが会社の利益最大化生産量となる。
ステップ2. 独占的競争者は、どのような価格を課すかを決定する。 企業がその利益最大化生産量を決定したとき、それは次にそれが出力のその量に請求できるものを見つけるために、その知覚需要曲線に見ることができます。 グラフでは、このプロセスは、それが会社の需要曲線を打つまで、利益最大化量を通して上に到達する垂直線として示すことができる。
独占的競争相手が数量と価格についての決定を行うプロセスは,独占企業がそのような決定を行う方法と似ているが,2つの違いを覚えておく価値がある。 第一に、独占企業も独占的競争企業も下り勾配の需要曲線に直面しているが、独占企業の知覚される需要曲線は市場の需要曲線であり、独占的競争企業の知覚される需要曲線はその製品の差別化の程度と直面する競争相手の数に基づいていることである。 第二に、独占企業は参入障壁に囲まれており、参入を恐れる必要はないが、利益を得る独占的競争者は、類似の、しかし差別化された製品を持つ企業の参入を期待しなければならない。
Try It
Calculating Profits
独占的競争者が供給すべき利益最大化生産量を決定したら、次はどれだけ利益を得ているか計算する。 完全競争や独占のときと同じプロセスを用いる。 これは、表2からのデータを表1まで拡張し、最後の列に平均総費用を入れたものを用いて、図2に示す。
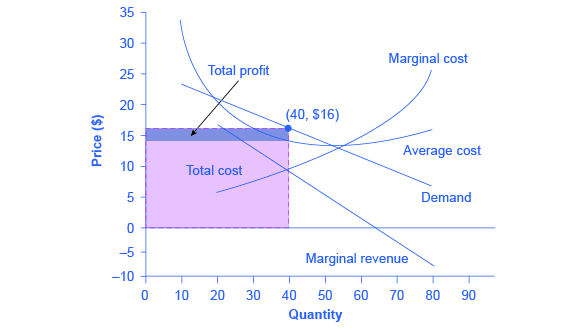
図2. 独占的競争相手の利益の計算。 利益を計算するには、利益最大化量である40から始める。 次に総収益を求める。これは高さP=16ドル×底辺Q=40の長方形の面積である。 次に総費用を求めます。これは高さACの長方形の面積$14.50にQの底辺=40を掛けたものです。 2つの面積の差が利益であり、図の総費用の上にある小さな長方形である。
| 表2. 収益とコストのスケジュール。 平均コストを含む | ||||||
|---|---|---|---|---|---|---|
| 数量 | 価格 | 総収入 | 限界収入 | 総コスト | 限界費用 コスト | 平均コスト |
| 10 | $23 | $230 | – | $340 | – | $34 |
| 20 | $20 | $400 | $17 | $400 | $6 | $20 |
| 30 | $18 | $540 | $14 | $480 | $8 | $16 |
| 40 | $16 | $640 | $10 | $580 | $10 | $14.50 |
| 50 | $14 | $700 | $6 | $700 | $12 | $14 |
| 60 | $12 | $720 | $2 | $840 | $14 | $14 |
| 70 | $10 | $700 | -$2 | $1,020 | $18 | $14.57 |
| 80 | $8 | $640 | -$6 | $1,280 | $26 | $16 |
まず、限界収入が限界費用に等しい、利益最大化レベルの生産量を特定するところから始める。 これはQ=40である。 次に、価格と平均原価の差である利潤率を求めます。 価格は$16で、これは数量が40に等しい場合の需要曲線から読み取れます。 平均コストは14.50ドルで、これは数量が40に等しい場合の平均コスト曲線から読み取ることができます。 利益率は、その会社が販売する各単位について、$16.00 – $14.50 = $1.50です。 また、総収益から総費用を差し引いたものを利益とすることもできます。 総収益は価格×数量、または$16.00×40=$640である。 これは、原点から始まり、価格16ドルまで上がり、需要曲線まで行き、数量40まで下がり、原点に戻る長方形の面積である。 総費用は平均費用×数量で、$14.50×40=$580です。 これは、原点から始まり、縦軸を平均コスト$14.50まで上がり、平均コスト曲線を越え、数量40まで下がり、原点に戻る長方形の面積です。 利益は、2つの領域の差、$640 – $580 = $60です。 これは、総原価の上にある長方形の面積、つまり価格から平均原価を引いたものに数量をかけたものとしてグラフに表示されます。 もし、会社が経済的利益をゼロにしていたら、総収益と総費用の長方形は同じになり、利益の長方形は存在しないことに注意してください。 損益分岐点は、需要曲線が平均費用と交差するところで発生するので、P = ACです。 また、会社が損失を出していた場合、負の利益(つまり損失)は総収入の上にある長方形になることに注意してください。
Try It
Contribute!
このページを改善するもっと知る