一般化線形モデルのチュートリアルでは、線形回帰、ロジスティック回帰などの様々なGLMについて学びました。 TechVidvanのRチュートリアル・シリーズのこのチュートリアルでは、Rでの線形回帰を詳しく見ていきます。 R線形回帰とは何か、Rでどのように実装するかを学びます。最小二乗推定法を見て、モデルの精度を確認する方法も学びます。

では、早速始めましょう。

Linear Regression in R

Linear Regression in R is a method used to predict the value of a variable using the value(s) of one or more input predictor variables.This uses the method of the linear regression in R…Linesar R..Linesar Regression in R…Linear Regression in R….Linesar Regression in the value of the variables with the value (s) of one or more input predictor variables. 線形回帰の目的は、目的の出力変数と入力予測変数の間に線形関係を確立することです。

連続変数 Y を 1 つ以上の入力予測変数 Xi の関数としてモデル化し、Xi の値のみが既知の場合に Y の値を予測するためにその関数を使用できるようにすること。 このような線形関係の一般的な形式は次のとおりです：

Y=?0+?1 X

ここで、?0 は切片
、.1 は傾きです。

Rの線形回帰の種類

Rの線形回帰には2種類あります：

• 単回帰
• 重回帰

これらを一つずつ見ていきましょう。

Simple Linear Regression in R

単回帰は、2つの連続変数間の線形関係を見つけることが目的です。 決定論的関係とは、一方の変数の値が他方の変数の値を使用して正確に求められるものである。 決定論的関係の例としては、キロメートルとマイルの関係があります。 キロメートルの値を使えば、マイル単位の距離を正確に求めることができる。 統計的関係は正確ではなく、常に予測誤差がある。 たとえば、十分なデータがあれば、身長と体重の関係はわかりますが、必ず誤差があり、例外的なケースも存在します。

単線回帰の考え方は、両変数の与えられた値に最も合う直線を見つけることです。 この直線は、従属変数の値が欠落しているときに、その値を見つけるのに役立ちます。

例題を使って、これを勉強してみましょう。 500人の身長と体重からなるデータセットがある。 我々の目的は、身長と体重の関係を定式化する線形回帰モデルを構築することで、モデルへの入力として身長（Y）を与えると、最小限の誤差で体重（X）を返してくれるようにすることである

Y=b0+b1X

b0とb1の値は誤差が最小になるように選択する必要がある。

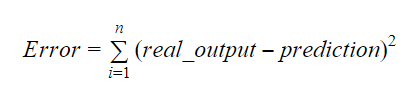
我々は次のように傾きまたは係数を計算できる：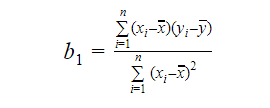

b1 の値は、従属変数と独立変数の関係の性質への洞察を与えてくれる。

• もしb1 > 0なら、変数は正の関係、すなわち
• b1 < 0なら、変数は負の関係、すなわち、xの増加はyの減少をもたらす。

b0または切片の値は、次のように計算することができます：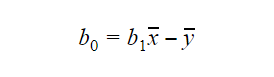
における切片 b0の値もモデルに関する多くの情報を与えることができ、その逆も同様です：

モデルにはx=0が含まれていなければ、b1なしでは予測が無意味になる。 モデルがどの時点でもb0だけで、b1が入っていないためには、その時点でxの値が0でなければならないのです。 身長などの場合、xが0になることはなく、人の身長も0にはならないので、b0だけのモデルは意味がありません。

b0の項がない場合、モデルは原点を通過してしまい、予測値や回帰係数（傾き）に偏りが生じます。

Rにおける重回帰

重回帰は単回帰の拡張版です。 重回帰では、複数の予測変数の値を用いて、対象変数の値を予測できる線形モデルを作成することを目的とする。 このような関数の一般的な形式は次のようになります：

Y=b0+b1X1+b2X2+…+bnXn

モデルの精度の評価

モデルの品質と精度を評価する方法はいろいろとあります。 7061>

R-Squared

データにおける真の情報は、その中に伝えられる分散である。 R2乗は対象変数(y)の変動のうち、モデルによって説明される割合を示している。 我々は、次の式を使用してモデルのR2乗測定を見つけることができます：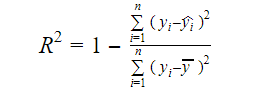

Where,

• yi is the fitted value of y for observation i
• y is the mean of Y.

R-2 乗の低い値は、モデルの低い精度を意味しています。 しかし、R2乗の数値は必ずしも最終的な決め手にはならない。

調整後R2乗

モデル中の変数の数が増えると、R2乗の値も大きくなる。 これは、新たに追加された変数によって説明される変動にも誤差を生じさせる。 そこで、多変数のR二乗の式を調整する。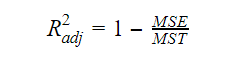
ここで、MSEはMean Standard Errorの略で、

そしてMSTはMean Standard Totalの略で次のように与えられる：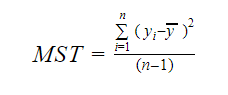

ここでnは観測値、qは係数の個数である。

R2乗と修正R2乗の関係は: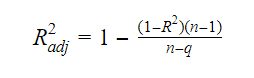

標準誤差とF統計

標準誤差とF統計はともにモデルの適合度の尺度である。 標準誤差とF統計量の計算式は次のとおりです。

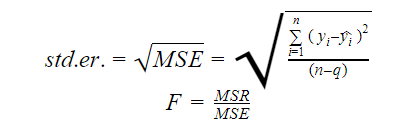
Where MSR stands for Mean Square Regression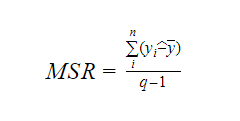

AICとBIC

赤池情報量基準とベイズ情報量は統計モデルの適合度の測定基準であり、赤池の場合はAIC、ベイズの場合はBICが使用される。

AIC=(-2)*ln(L)+2*k
BIC=(-2)*ln(L)+k*ln(n)

ここで、

• Lは尤度関数、
• kはモデルパラメータの数、
• nはサンプルサイズである。

Rのlm関数

Rのlm()関数は線形モデルのフィッティングを行う関数です。 回帰や分散・共分散の分析を行うことができます。 lm関数の構文は以下の通りです：

lm(formula, data, subset, weights, na.action,method = "qr", model = TRUE, x = FALSE, y = FALSE, qr = TRUE,singular.ok = TRUE, offset, …)

Where,

• formula is an object of class “formula” and is a symbolic representation of the model to fit,
• data is the data frame or list that contains the variables in the formula(data is an optional argument.
• subset はフィット処理で使用される観測値のサブセットを含むオプションのベクトル、
• weights はフィット処理で使用される重みを指定するオプションのベクトル、
• na.actionはデータ中にNAがあった場合にどうするかを示す関数、
• methodはモデルのフィット方法を示す、
• model, x, y, qrは対応する値を出力で返すかどうかを制御する論理値である。
• model: モデルフレーム
• x: モデル行列
• y: 応答
• qr: qr分解
• singular.ok は特異フィットを許可するかどうかを制御する論理、
• offset はモデルで使用する既知の予測変数、
• …. …は低レベルの回帰関数に渡される追加の引数です。

Rにおける線形回帰の例

今のところ理論はこれで十分です。 それでは、これらをどのように実装するかを見ていきましょう。 Rの線形回帰を使って、lm()関数の助けを借りて、線形モデルをあてはめようとしています。 また、この後、モデルの適合の質をチェックします。 Rの基本パッケージでデフォルトで提供されているcarsデータセット

1 を使ってみましょう。 まずは、このデータセットに慣れるために、グラフィカルな分析から始めましょう。

Scatter.smooth() 関数を使って、データセットの散布図を作成します。

scatter.smooth(x=cars$speed,y=cars$dist,main="TechVidvan Dist ~ Speed")

Output

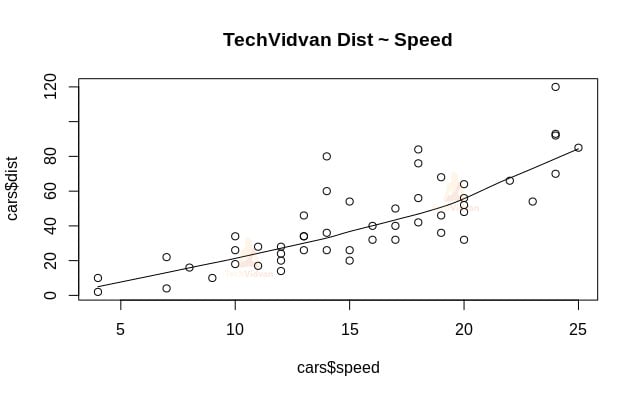
散布図は距離と速度に正の相関があることを表しています。 これは、2つの変数の間に直線的な増加関係があることを示唆しています。 線形関係はデータに線形モデルを当てはめるための基本的な仮定なので、これはデータを線形回帰に適したものにします。 さて、線形回帰がデータに適していることが確認できたので、lm()関数を使って線形モデルを当てはめることができます。

Linear_model <- lm(dist~speed,data=cars)print(Linear_model)

出力

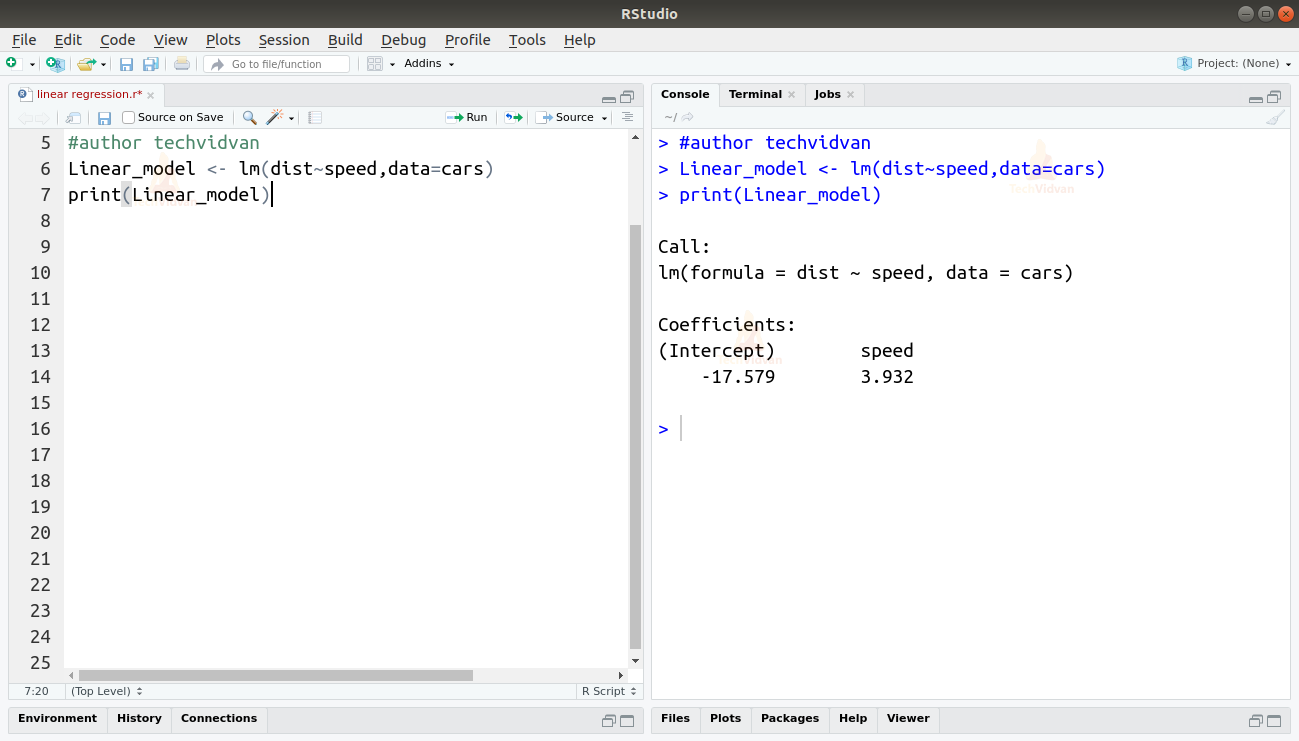
lm()関数の出力には、切片と速度の係数が表示されます。 したがって、距離と速度の線形関係は次のように定義されます：

Distance=Intercept+coefficient*speed

Distance=-17.579+3.932*speed

3. さて、モデルをあてはめたところで、その適合度、品質をチェックしましょう。 summary()関数を使って線形モデルのサマリーをチェックすることから始めましょう。

summary(Linear_model)

Output

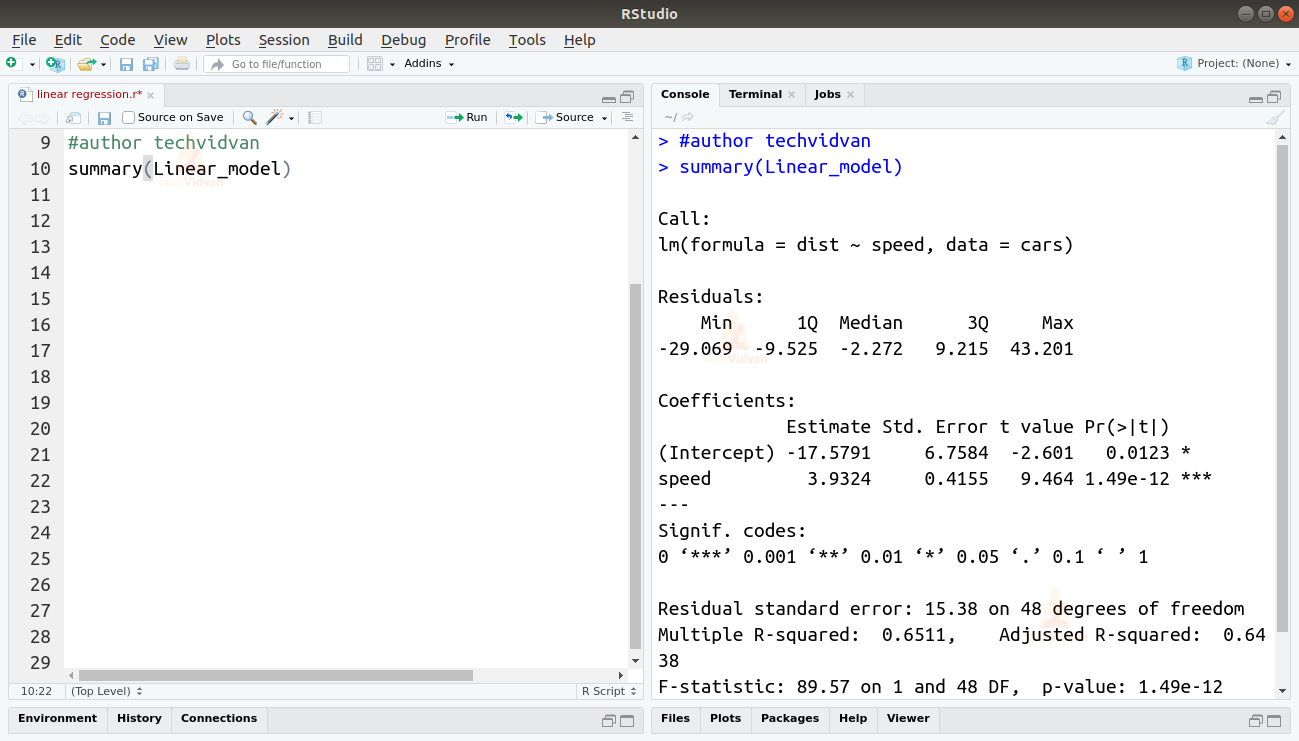
関数が、モデルの適合度を診断するのに役立ついくつかの重要な指標を与えてくれます。 p-値は、モデルの適合度の重要な尺度である。 p値があらかじめ決められた統計的有意水準（理想的には0.05）より大きいと、モデルは適合していないと言われる。

また、summaryはt値も提供してくれる。
また、AIC()関数やBIC()関数を用いて、AICやBICを求めることができる。

AIC(Linear_model)BIC(Linear_model)

出力

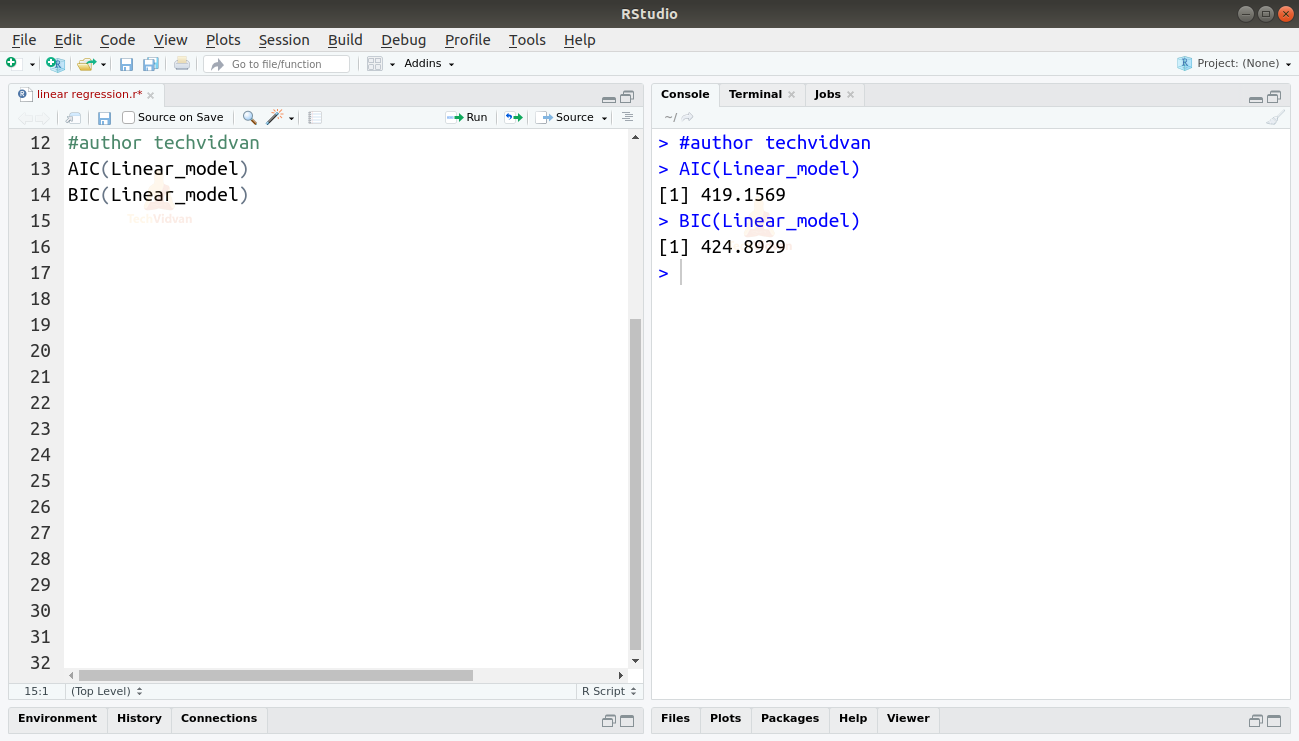
AICとBICスコアを最も低くするモデルが最も好ましい。

まとめ

TechVidvan の R tutorial シリーズのこの章では、線形回帰について学びました。 単回帰と重回帰について学びました。 そして、R2、修正R2、標準誤差、F統計、AIC、BICなど、モデルの品質や精度を評価するための様々な指標を学びました。 そして、Rで線形回帰を実装する方法を学び、Rでモデルの適合の質をチェックしました。

Do share your rating on Google if you liked the Linear Regression tutorial.

.