
信号フロー解析の項で述べたように、何らかの形で信号フロー解析を行うことが負帰還増幅器を扱う最も一般的な方法ですが、2つの2ポートで表現することが教科書に最も多く紹介されている方法ですので、ここで紹介します。 これは、アンプの2ブロックの回路分割を維持したまま、ブロックをバイラテラルにすることができる。 1373>
電子増幅器は電流または電圧を入出力とするので、4種類の増幅器が考えられる(2つの入力のいずれかと2つの出力のいずれかが可能)。 増幅器の分類を参照。 帰還増幅器の目的は、4種類の増幅器のいずれでもよく、開ループ増幅器とは必ずしも同じ種類でなくてもよく、それ自体もこれらの種類のいずれでもよい。 例えば、オペアンプ(電圧増幅器)を電流増幅器にアレンジすることも可能です。
どのタイプの負帰還増幅器も、2ポート・ネットワークの組み合わせで実装できます。 2ポート・ネットワークには4つのタイプがあり、目的のアンプのタイプによって、2ポートの選択と、図に示す4つの異なる接続トポロジのうちの1つの選択が決定されます。 これらの接続は、通常、直列またはシャント(並列)接続と呼ばれます。 図では、左の列がシャント入力、右の列がシリーズ入力を示しています。 上段は直列出力、下段はシャント出力です。 接続と2ポートのさまざまな組み合わせは、下の表に示すとおりです。
| フィードバックアンプのタイプ | 入力接続 | 出力接続 | 理想フィードバック | ツーポートフィードバック |
|---|---|---|---|---|
| 電流 | シャント | シリーズ | CCCS | g-parameter |
| 交差抵抗 | シャント | CCVS | y-> | |
| Transconductance | Series | VCCS | z-…parameter | |
| Voltage | Series | Shunt | VCVS | h-parameter |
例えば、以下のようになります。 電流帰還型アンプの場合、出力からの電流をサンプリングして帰還させ、入力からの電流と合成します。 したがって、理想的には、フィードバックは(出力)電流制御電流源(CCCS)を用いて行われ、2ポートネットワークを用いた不完全な実現もCCCSを組み込む必要があり、つまり、フィードバックネットワークにはgパラメータ2ポートが適切な選択となる。 ここでは、漸近利得モデルの記事で扱った回路を用いて、ほとんどの教科書で使われている2ポート法を紹介する。

図3は帰還抵抗Rf付きの2トランジスタ増幅器を示したものだ。 この回路を解析して、利得、負荷からアンプを見た出力インピーダンス、ソースからアンプを見た入力インピーダンスの3項目を求めることが目的である。
帰還回路網を2ポートに置き換える編集
最初のステップは、帰還回路網を2ポートに置き換える。 2ポートにはどのような部品があるのでしょうか。
2ポートの入力側にはRfがあります。 Rfの右側の電圧が変化すると、入力トランジスタのベースに入る電流から差し引かれるRfの電流が変化します。 つまり、2ポートの入力側は、抵抗R2の上端の電圧で制御される従属電流源なのです。
アンプの2段目は、入力トランジスタのコレクタの電圧をR2の上端に伝達する、単なる電圧フォロワと言えるかも知れません。 つまり、モニターされる出力信号は、実際には入力トランジスタのコレクタの電圧なのです。 この考え方は正しいが、その場合、ボルテージフォロワ段はフィードバックネットワークの一部となる。 図 4: g パラメータのフィードバック・ネットワーク
別の見解として、R2 の上端の電圧は出力トランジスタのエミッタ電流で設定されるというものがある。 この場合、R2とRfで構成される完全受動的なフィードバック・ネットワークになります。 フィードバックを制御する変数はエミッタ電流であるから、フィードバックは電流制御電流源(CCCS)である。 4つの利用可能な2ポートネットワークを検索し、CCCSを持つ唯一のネットワークは、図4に示すgパラメータ2ポートであることを発見しました。 次の課題は、図4の2ポートがR2とRfで構成されるLセクションと電気的に等価になるように、gパラメータを選択することである。 V1=0で2ポートの右側のVCVSを短絡させる場合と、I2=0で左側のCCCSを開回路とする場合である。 この2つの場合の代数は単純で、すべての変数を一度に解くよりずっと簡単だ。 2ポートとL部が同じ挙動をするようなgパラメータの選択は、下表の通りです。
| g11 | g12 | g21 | g22 |
|---|---|---|---|
1 R f + R 2 {displaystyle {frac {1}{R_{theaterm {f} }}} {displaystyle {hat? }+R_{2}}}}
 |
– R 2 R 2 + R f {displaystyle -{frac {R_{2}}{R_{2}+R_{mathrm {f}}} }}}}
 |
R 2 R 2 + R f {displaystyle {}frac {R_{2}}{R_{2}+R_{mathrm {f}}} }}}}
 |
R 2 / / R f {displaystyle R_{2}//R_{mathrm {f} }} {displaystyle R_{2}/R_{mathrm {f }\ }
 |
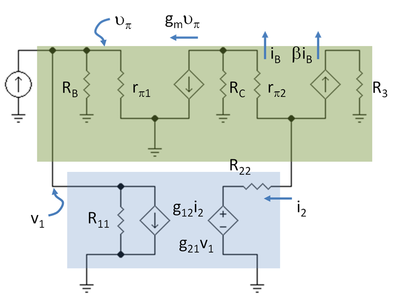
図5:フィードバックネットワークに2ポートを用いた小信号回路、上段斜線枠:メインアンプ、下段斜線枠:RfとR2によるL部をフィードバック2ポートに置換した場合。
小信号回路編集
次に、トランジスタのハイブリッドパイモデルを使って、2ポートを配置したアンプの小信号回路図を描きます。 図5は、R3 = RC2 // RLとR11 = 1 / g11、R22 = g22の表記で回路図を示しています。
Loaded open-loop gainEdit
図3は出力ノードを示していますが、出力変数の選択はしていません。 有用な選択は,アンプの短絡電流出力である(短絡電流利得につながる)。 この変数は、他の選択肢(例えば、負荷電圧または負荷電流)のいずれかに単純につながるため、短絡電流利得は以下で求められます。
最初に、負荷開ループ利得が求められます。 g12=g21=0として帰還をオフにして、帰還回路網の抵抗単体でアンプの利得がどれだけ変わるかを求めるものです。 この計算は、R11、RB、rπ1がすべて並列で、v1=vπなので、とても簡単です。 R1 = R11 // RB // rπ1 とします。 また、i2 = -(β+1)iBとします。 開ループ電流ゲインAOLの結果は:
A O L = β i B i S = g m R C ( β β + 1 ) ( R 1 R 22 + r π 2 + R C β + 1 ) …となります。 {Displaystyle A_{mathrm {OL} }={frac {beta i_{mathrm {B}}} }}{i_{mathrm {S}} のようになります。 }}}=g_{m}R_{mathrm {C}} }left({}frac {}beta }{}right)\left({}frac {R_{1}}{R_{22}+{}frac {r_{pi 2}+R_{}mathrm {C}) }}{beta +1}}}right)\.}.

Gain with feedbackEdit
古典的なフィードバックの考え方では、VCVSで表されるフィードフォワード(つまり、g21 v1)は無視されます。 そのため、図5の回路は図1のブロック図と似ており、フィードバックによる利得は次のようになる:
A F B = A O L 1 + β F B A O L {displaystyle A_{mathrm {FB}}} 。 }={frac {A_{mathrm} {OL}} }}{1+{beta }_{mathrm} {FB} A_{mathmrm {OL}} のようになります。 }}}}

A F B = A O L 1 + R 2 R 2 + R f A O L , {}displaystyle A_{mathrm {FB}} }={frac {A_{mathrm {OL}}} }}{1+{frac {R_{2}}{R_{2}+R_{mathrm {f}}}A_{mathrm}}A_{mathrm {OL}} }}} ,}

ここで、フィードバック係数βFB=-g12である。 1373>
入力抵抗と出力抵抗Edit

信号源と負荷をより一致させるためにフィードバックは使用されます。 たとえば、電圧源を抵抗負荷に直接接続すると、電圧分割により信号が失われることがありますが、負帰還増幅器を挿入すると、信号源から見た見かけの負荷が増加し、負荷から見た見かけの駆動インピーダンスが減少するため、電圧分割による信号減衰を避けることができます。 この利点は電圧増幅器に限られたものではなく、電流増幅器、トランスコンダクタンス増幅器、トランスレジスタンス増幅器にも同様のマッチングの改善が可能です。
こうしたフィードバックのインピーダンスに対する効果を説明するために、まず2ポート理論がどのように抵抗決定にアプローチするかを脱線し、次にそれを手元のアンプに応用します。
抵抗値決定の背景編集
図6は、フィードバック電圧増幅器(左)とフィードバック電流増幅器(右)の入力抵抗を求めるための等価回路である。 電圧増幅器の場合、帰還回路網の出力電圧βVoutは、ループを伝わる入力電圧Vxと逆極性で直列に印加される(ただし、接地に対しては同極性)。 その結果,増幅器入力抵抗 Rin の実効電圧と電流が減少し,回路の入力抵抗が増加します(見かけ上,Rin が増加したように見えるかもしれません)。 その新しい値は、ミラーの定理(電圧の場合)や基本的な回路法則を適用して計算することができる。 したがって、Kirchhoffの電圧法則は次のようになる:
V x = I x R i n + β v o u t , {}displaystyle V_{x}=I_{x}R_{mathrm {in} }+beta v_{mathrm {out}. } ,}

ここで、vout = Av vin = Av Ix Rinとする。 この結果を上式に代入し、帰還増幅器の入力抵抗について解くと、
R i n ( f b ) = V x I x = ( 1 + β A v ) R i n となります。 {R_{mathrm {in}. }(fb)={frac {V_{x}}{I_{x}}=Thinkleft(1+Thinkbeta A_{v} Right)R_{mathrm {in}. }\ .}

この例と出力抵抗の場合の同様の例からの一般的な結論は、入力(出力)での直列フィードバック接続は、入力(出力)抵抗を係数(1+βAOL )だけ増加させ、ここでAOL=開ループゲインです。 その結果、回路入力(入力抵抗Rinだけでなく)を流れる総電流が増加し、その間の電圧が減少するので、回路入力抵抗は減少する(Rinは見かけ上減少する)。 その新しい値は、二重ミラーの定理(電流の場合)または基本的なキルヒホッフの法則を適用することによって計算することができます:
I x = V i n R i n + β i o u t . {I_{x}={frac {V_{mathrm {in} }}{R_{mathrm {in}} }}+β i_{mathrm} {out} }\ .}

ここで、iout = Ai iin = Ai Vx / Rinである。 この結果を上式に代入し、帰還増幅器の入力抵抗について解くと、
R i n ( f b ) = V x I x = R i n ( 1 + β A i ) … となります。 {R i n ( f b ) = V x I x = R i n ( 1 + β A i ) . }(fb)={frac {V_{x}}{I_{x}}}={frac {R_{mathrm {in}}} }}{left(1+Θbeta A_{i}right)}} .}.

この例と出力抵抗の場合の同様の例から一般的に言えることは、入力(出力)での並列帰還接続は入力(出力)抵抗を係数(1 + β AOL )だけ減少させ、AOL = オープンループゲインとなる。
これらの結論は、任意のノートンまたはテベニン駆動、任意の負荷、および一般的な2ポートフィードバックネットワークのケースを扱うために一般化することができる。 しかし、結果は主増幅器が2ポートとして表現されることに依存します。つまり、結果は入力端子に入る電流と出る電流が同じであることに依存し、同様に、一方の出力端子から出た同じ電流は他方の出力端子に入る必要があります。
定量的な詳細とは関係なく、より広い結論は、フィードバックは入力と出力インピーダンスを増加または減少させるために使用することができるということです。
例のアンプへの適用編集
次にこれらの抵抗結果を図3および図5のアンプに適用します。 利得を下げる改善係数、すなわち( 1 + βFB AOL)がそのまま増幅器の入出力抵抗へのフィードバックの効果を決定する。 分路接続の場合、入力インピーダンスはこの係数分減少し、直列接続の場合、インピーダンスはこの係数分乗算される。 ただし、フィードバックによって変化するインピーダンスは、図5のアンプでフィードバックをオフにしたときのインピーダンスであり、フィードバックネットワークの抵抗によるインピーダンスの変化も含まれる。
したがって、フィードバックをオフにした状態でソースが見る入力インピーダンスはRin = R1 = R11 // RB // rπ1 で、フィードバックをオンにした状態(ただしフィードフォワードなし)
R i n = R 1 1 + β F B A O L , {displaystyle R_{mathrm {in}… }={frac {R_{1}}{1+{Подкли}}{{mathrm {FB}}} A_{mathrm {OL}} のようになります。 }}} ,}

ここで、入力接続がシャントであるため、除算が使用されます:フィードバック2ポートがアンプの入力側で信号源と並列に接続されます。 注意点です。 AOLは、フィードバックネットワークの抵抗によって修正された、上記で見つかった負荷開ループゲインである。 図5の負荷は、出力トランジスタのコレクタに接続されているため、出力電流源の無限インピーダンスによってアンプ本体から分離されている。 したがって、フィードバックは出力インピーダンスに影響を与えず、図3の負荷抵抗RLで見るように、単純にRC2のままです。
その代わりに、フィードバック回路に直列接続されている出力トランジスタのエミッタ(コレクタの代わり)に現れるインピーダンスを求めたい場合、フィードバックにより、この抵抗は改善係数(1 + βFB AOL)だけ増加することになります。
負荷電圧と負荷電流編集
上で導いた利得は、出力トランジスタのコレクタでの電流利得です。 この利得と電圧をアンプの出力としたときの利得を関連づけると、負荷RLでの出力電圧はオームの法則によりvL=iC(RC2||RL)としてコレクタ電流に関係することに気がつきます。 したがって、電流利得に RC2 || RL を乗じれば、抵抗利得 vL / iS が求まります:
v L i S = A F B ( R C 2 ∥ R L ) . {L} . }}{i_{mathrm {S}} のようになります。 }}=A_{mathrm {FB} }(R_{mathrm {C2} }parallel R_{mathrm {L} })\ .}.

同様に、アンプの出力を負荷抵抗RLの電流とすると、電流分割で負荷電流が決まり、ゲインは次のようになる: i L i S = A F B R C 2 R C 2 + R L . }}{i_{mathrm {S}} のようになります。 }}=A_{mathrm {FB}} }{frac {R_{mathrm {C2}} }}{R_{mathrm {C2}} }+R_{mathmatrm {L}} }}}\ .}

主アンプブロックは2ポート? 編集

図7は小信号回路図であり、主増幅器とフィードバック2ポートを斜線枠で囲んでいる。 フィードバック2ポートは、入力ポートではIinがポートに入ったり出たり、同様に出力ではIoutが入ったり出たりというポート条件を満たしている。
主増幅器ブロックも2ポートなのだろうか。 主増幅器は上部の斜線枠の中です。 グランド接続にはラベルが貼られています。 図7は、主増幅器がそうなるようにグラウンド接続を選ばないと、入力と出力でポート条件を満たさないという興味深い事実を示しています。 例えば、入力側では、主増幅器に入る電流はISである。 この電流は、帰還回路網、バイアス抵抗RB、入力トランジスタのベース抵抗rπの3通りに分けられる。 主増幅器のポート条件を満たすには、この3つの成分を主増幅器の入力側に戻す必要があります。つまり、G1と書かれたグランドリードをすべて接続し、エミッタリードGE1も接続する必要があります。 同様に、出力側では、すべてのグランド接続G2を接続し、さらにグランド接続GE2も接続しなければならない。 そして、回路図の一番下、フィードバック2ポートの下、アンプブロックの外側で、G1はG2に接続されています。 これで強制的にグランド電流が計画通りに入力側と出力側に振り分けられる。 この接続の配置は、入力トランジスタのエミッターをベース側とコレクター側に分割することに注意してください。物理的に不可能なことですが、電気的には、回路はすべてのグランド接続を1つのノードとして見るので、このフィクションは許可されます。 この人為性はこの方法の弱点である。ポート条件はこの方法を正当化するために必要であるが、回路は実際にグランド接続間で電流がどのように取引されるかに影響されない。
しかし、グランド条件の可能な配置がポート条件につながらない場合、回路は同じように振舞わないかもしれない。 入出力インピーダンスを決定するための改善要因(1 + βFB AOL)が機能しないかもしれない。 この状況は厄介で、2ポートを作れないということは、現実的な問題(不可能である)を反映しているかもしれないし、想像力の欠如(例えば、エミッタノードを2分割することを思いつかなかった)を反映しているかもしれないからである。 Spice を使用して例をシミュレートし、改善因子を使用して結果を比較するか、テストソースを使用してインピーダンスを計算し、結果を比較します。
より実用的な選択は、2 ポートアプローチを完全にやめて、Rosenstark 法、Choma 法、および Blackman の定理の使用など、信号フローグラフ理論に基づくさまざまな代替手段を用いることです。 小信号デバイスのモデルが複雑であったり、利用できない場合(例えば、デバイスが測定やSPICEシミュレーションによる数値的なものしか知らない場合)には、この選択が望ましいかもしれない
。