
今回は、品質を維持するための基本を紹介します。
これには、品質保証、品質管理、計測学が含まれます。 品質保証は、品質要求が満たされるという確信を得るために使います。 品質管理は、要求事項が満たされていることを確認するために使用します。 これは微妙な違いであり、実際にはこの用語は互換的に使われることもある。 計測学は測定の科学です。 世界中で行われる計測の結果を、自信を持って比較できるようにするための方法です。
これらの原則は製品にもサービスにも適用できますが、ここでは製造に焦点を当て、その文脈でこれら3つの基本概念がどのように関係し合っているかを説明します。 そのため、具体的な手法の詳細や、数学的な話には触れませんでした。 それは後日の記事に譲ることにします。
測定の起源
エジプト人は、大規模な建設プロジェクトで石がぴったり合うように、定期的に校正しながら測定基準を使用しました。 しかし、近代的な品質システムは産業革命の時代に実際に始まった。 それ以前は、機械製品は職人によって作られ、職人は組み立てに必要な部品をひとつひとつ調整していた。 つまり、機械も部品も一点ものだったのです。 もし、部品交換が必要な場合は、職人が新しい部品を取り付ける必要がありました。
18世紀後半、フランスの兵器メーカーは、標準的な部品を使ったマスケットを作るようになった。 このため、軍隊は予備部品を携帯し、壊れた部品とすぐに交換することができた。 これらの交換可能な部品は、依然として組立品に適合するように加工されていましたが、各部品を個々の銃に適合させるのではなく、マスター部品に適合させるようにしました。
それから数年後、アメリカの銃器メーカーがこの方法を使い始めたが、訓練を受けていない労働者に合わせてアレンジしていった。 マスターパーツに合わせるゲージをヤスリで削り、作業者はそのゲージを使って治具や生産機械をセットし、さらにそのゲージでパーツをチェックするのです。 こうして、1台の機械が何台も並び、1つの作業を熟練者でなくとも、正確に生産することができるようになった。 そして、その部品を素早く組み立てて、複雑な機械を作ることができるようになった。
こうして近代的な製造業の基礎が築かれたが、フォードがこのアイデアを動く生産ラインに適用する100年以上前のことである。
キャリブレーション、真値、および測定誤差
マスターパーツ、ゲージ、単一使用機械のシステムは、製品全体が単一の工場で生産されていたときに機能しました。 現代のグローバルサプライチェーンには、別のシステムが必要です。
物理的なマスターパーツを持つ代わりに、図面やデジタルCADモデルを持つのです。 指定された公差は、部品が一緒にフィットし、意図されたとおりに機能することを保証します。 すべてのメーカーが1つのマスターパーツにゲージをセットしに来るのではなく、測定器を校正してもらっています。 そして、その測定器を使って生産機械をセットし、生産されたパーツをチェックするのです。
すべての品質は、このキャリブレーション・プロセスに依存しています。
理解すべき最も重要な概念は、すべての測定には不確かさがあるということです。 もし私がこのテキストの高さを推定するよう頼んだら、「約4mmです」と言うかもしれません。 この「約」という言葉を使うことは、あなたの見積もりにはいくらか不確かさがあることを意味します。
実際、私たちは何事も正確な真の値を知ることはできず、すべての測定は実際には推定値であり、何らかの不確実性を持っています。 測定結果と真の値との間の差が測定誤差です。 真の値を知ることができないので、誤差も知ることができない:これらは知ることができない量である。
私たちが身の回りの世界について定量化できるのは測定結果だけであり、その不確かさは非常に小さいものであっても、常に何らかの不確実性を持っているのです。
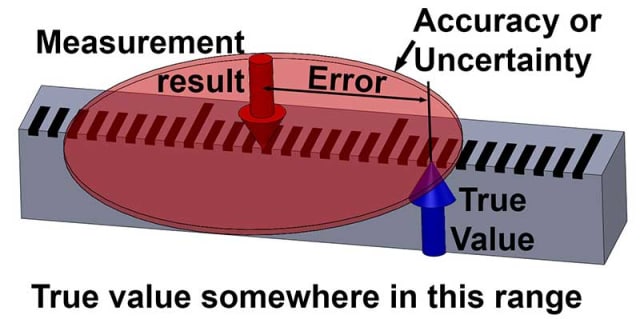
このテキストの高さを「4mm程度、1mm程度の誤差」と見積もった場合、これで不確かさにいくつかの限界を設定したことになります。 しかし、あなたはまだそれが真実であると100%確信することはできません。
ある程度の確信、たとえば95パーセントの確信を持って、それが正しいと言えるかもしれません。 もし、その限界を2mm程度まで広げると、信頼度はおそらく99%にまで高まります。 つまり、不確かさは、真の値が存在するという確信のレベルを示す、ある境界を与えるのです。
OK、哲学の授業は終わり!
今後の投稿では、これらのアイデアと、特定の信頼度に対する不確実性がどのように計算されるかを拡大解釈します。
不確かさと品質
一旦、測定の不確かさ(または「精度」)を決定すると、次にこれを適用して、部品が指定した公差に適合しているかどうかを判断することができます。 例えば、ある部品が100 mm +/- 1 mmであると指定されているとします。 これを測定したところ、100.87mmという結果が出ました。
その部品は仕様通りですか?
答えは簡単で、「わからない、多分そうだろう、しかし我々の測定に誤差があり、実際にはその部品は101mm以上である。 もしかしたらさらに大きな誤差があり、実際には部品は99mm以下かもしれない!”ということです。
測定の不確かさがわからない限り、その部品が仕様の範囲内であることにどれだけ自信を持っていいのかがわかりません。 測定の不確かさが、測定結果が95%の信頼度で100.87 mm +/- 0.1 mmとなるように与えられたとしましょう。 これで、その部品は仕様の範囲内であると95%以上の信頼度で言うことができます。
ですから、測定の不確かさを理解し定量化することは、品質を維持するために非常に重要なことなのです。
さて、校正とそれに関連するトレーサビリティの概念について考えてみましょう。 これは不確かさの基本的な側面です。 校正は基準との比較であり、以下に説明する理由により、この比較の不確かさは常に含まれなければなりません。
トレーサブルな測定とは、一次標準に至るまで校正の切れ目のない連鎖を持つものです。 長さの測定の場合、一次標準はメートルの定義で、パリの国際度量衡局(BIPM)が実現したように、真空中で光が1/299792458秒間に進む距離です。
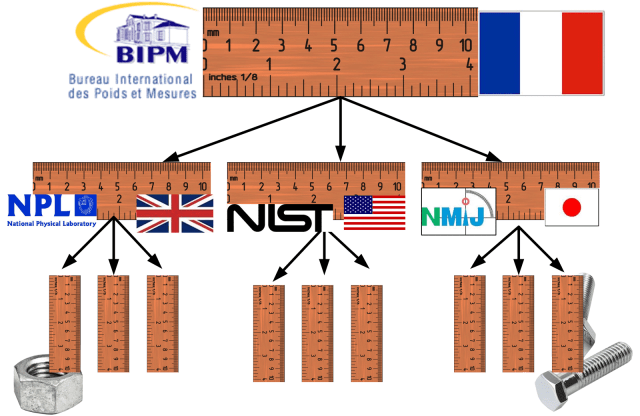
1930年代以降、インチは25.4mmと定義されており、したがって同じメートル標準にトレーサビリティがあります。 異なる国で製造された部品が互いに適合することを保証するために、すべての測定は同じ標準にトレーサブルでなければならない。
不確実性と誤差
測定の不確かさは、さまざまな原因から生じます。 これらのうちのいくつかは、結果に一貫した誤差、または偏りをもたらすことになる。
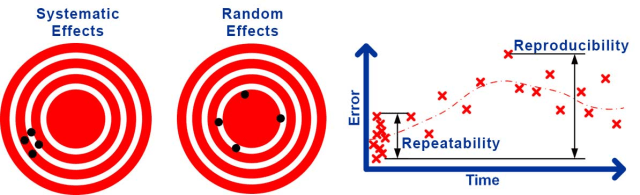
例えば、測定器が校正されたときに存在する未知の誤差は、それが使用されるたびに一貫した誤差につながります。 このような影響は、系統的な誤差をもたらす系統的な不確かさとして知られています。 他の原因では、測定が行われるたびにランダムに変化する誤差が生じます。
例えば、空気中の乱流はレーザー測定に小さな、ランダムに変化する摂動を引き起こすかもしれませんし、機械的な遊びやアライメントは機械的な測定にランダムに変化する誤差を引き起こすかもしれません。 この種の効果は、ランダムな誤差をもたらすランダムな不確かさとして知られています 。
ランダムな不確かさは、同じ条件下での結果のランダムな不確かさである「再現性」と、条件を変えたときのランダムな不確かさである「再現性」に分けるのが一般的である。
もちろん、条件が全く同じ、あるいは全く異なるということはありえないので、この区別はやや曖昧である。 変更される可能性のある条件としては、異なる時間、異なるオペレータ、異なる機器、異なる校正、異なる環境での測定が挙げられます。
測定の不確かさを定量化するために広く使用されている方法が2つあります。 校正機関や科学研究機関では通常、GUM (Guide to the Expression of Uncertainty in Measurement) に従って不確かさ評価を行っています。
GUM法では、まず測定結果に影響を与える可能性のあるすべての影響を検討します。 次に、これらの影響量の関数として測定結果を与える数学的モデルを決定する必要があります。 各入力量の不確かさを考慮し、「不確かさ伝播の法則」を適用することにより、測定の複合不確かさの推定値を算出することができます。
GUMアプローチは、個々の影響を考慮することから始まるため、ボトムアップと表現されることもあります。 各影響は通常、複合不確かさを計算するために使用される不確かさバジェットと呼ばれる表にリストアップされます。
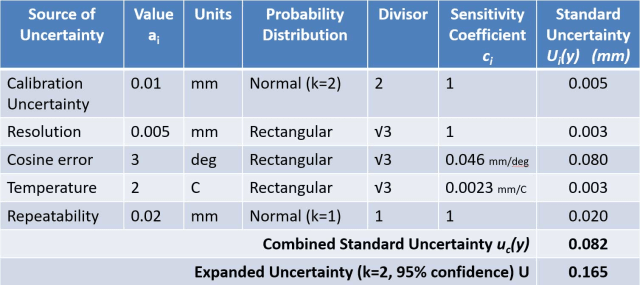
工業計測プロセスは通常、シックスシグマ手法の中で推奨されているように、また通常はAIAG (Automotive Industry Action Group) MSA Reference Manualのガイドラインに従って、計測システム分析 (MSA) のアプローチを使用して評価されています。
MSAでは、偏りや反復性、場合によっては再現性を判断するために、異なる条件下で繰り返し測定値を基準と比較するゲージ研究を実施します。
Type-1 Gage Studyは、最初にゲージのばらつきを理解するために通常実施されるクイックチェックです。 これは、1人の作業者が1つの校正済み基準部品を25回以上測定し、結果のばらつきや偏りを検討するものです。 この種の試験は、MSA以外ではしばしば繰返し性試験と呼ばれます。
ゲージの反復性と再現性(Gage R&R)研究は、測定プロセスのより詳細な理解を得るために使用されます。 通常、10個の部品を少なくとも3人の異なるオペレータがそれぞれ2回測定します。 そして,ANOVAと呼ばれる統計手法を使用して,どれだけの変動が機器(「ゲージ」)によって引き起こされ,どれだけがオペレータによって引き起こされるかを決定する. これにより、オペレーターの変更とその後の時間や環境の変化を再現性の条件の完全な表現とみなします。
MSAは、測定プロセスをブラックボックスとして大きく扱い、系統的およびランダムな不確かさを実験的に決定するので、トップダウンと呼ばれることもあります。 MSAの2つの重要な概念は、不確かさの同等物として使用される「精度」と、ランダムな不確かさの同等物として使用される「正確さ」である。
不確実性評価の利点は、すべての不確実性源を考慮することができ、適切に行われれば、不確実性の最も正確な推定値を与えることができることです。 この方法の問題点は、数学的モデルを作成できる計量士が必要なことと、人為的なミスにより重要な影響が省略されたり、間違って推定されたりする危険性があることである。
GUM法はまた、適用される補正の値が既知の状態で実施された個々の測定に対してのみ有効です。 したがって、工業的な測定プロセスの不確かさを予測するために、不確かさ評価を正しく適用することは困難である。
MSAはもっと簡単に適用でき、工業計測プロセスの精度の予測を提供することを目的としています。 この方法の問題点は、ある種の系統的な効果が無視され、再現性の条件が完全に表現されないことがあり、不確かさが過小評価されることである。
系統的効果の省略の例としては、バイアスを決定する際に、真の値として扱われる基準との比較が行われますが、実際には基準にも不確かさがあり、それは含まれるべきものです。 この方法は、再現条件をすべて変化させ、繰り返し測定したときの結果のばらつきにその影響を見ることができるようにすることに依存しています。 これらの条件を変化させる方法は、実際の測定プロセスで見られる変動を完全には反映しない可能性があります。
測定と品質保証
これまでは品質管理、すなわち部品が生産された後に測定によって仕様に適合していることをいかに証明するかに焦点をあててきた。 ここで、品質保証、つまり、プロセスが最初に良い部品を生産することを保証する方法について簡単に考えてみましょう。
このような品質の側面は、主に統計的工程管理(SPC)により扱われます。 あるプロセスを評価するために、いくつかの部品を作り、それを測定して製造プロセスのばらつきや偏りを判断することがあります。 これらの結果を直接与えるのではなく、部品の公差を工程の精度で割って工作機械能力( C P )、または工程の精度で割って工程能力( C PK )を与えるのが普通である。
SPCは多くの点でMSAと同等です。 ランダム効果および系統的効果を理解するためにトップダウン的なアプローチをとります。 しかし、測定値を評価するのではなく、プロセスの出力を評価するために使用されます。 一般的にMSAと同じ利点と欠点があり、これらが懸念される場合は、ボトムアップの不確かさ評価アプローチを使用することができます。
SPC内の用語が非常に異なるため、当初はMSAとSPCの間に根本的な違いがあるように思われるかもしれません。 しかし、共通原因変動(古い文献では偶然原因変動)は精度に相当し、短期変動は再現性に相当し、長期変動は再現性に相当し、特別原因変動(古い文献では割り当て可能原因変動)はバイアスに相当します。
また、SPCではプロセスが「統計的管理」にあることを保証することに、より大きな重点を置いています。 広い意味で、これは影響がランダムで正規分布し、重大な系統的影響があれば補正されることを意味します。 これはSPCの長所であり、不確かさ評価やMSAでは見落とされることがあります。
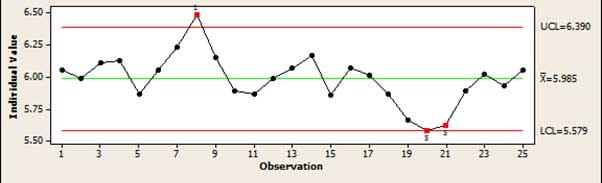
「コントロールされている」プロセスをチェックするためにSPCで使用される主なツールは管理図です。 これは、プロセスがドリフトしていたり、通常のランダムな変動では説明できないエラーが発生している場合に、プロセスをシンプルなグラフで表示するもので、簡単に発見することができます。 例えば、いくつかの点がすべて増加または減少している場合、これはプロセスがドリフトしていることを示しています。
この記事では、大きく複雑なテーマを広く概観することを試みました。 品質を維持するための基本的な原理を紹介しましたが、これらの方法を適用するために必要な数学には一切触れませんでした。
これらのトピックに関する今後の記事にもご期待ください。

Jody Muelaner博士の20年にわたるエンジニアリングキャリアは、機械設計から始まり、医療機器から製材所まであらゆるものに携わってきました。 2007年以来、彼はバース大学で、航空宇宙産業の大手企業と密接に協力しながら、新しい計測技術の開発に取り組んでいる。 この研究は現在、生産システムの不確実性モデリングに焦点を当て、SPC、MSA、計測学の要素を新しい数値メソッドでまとめています。 また、自転車のデザインにも関心を持っています。 詳しくは、彼のウェブサイトをご覧ください。