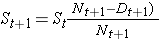私たちはしばしば、参加者の異なるグループ間で生存率（またはイベントの累積発生率）に差があるかどうかを評価することに関心があります。 例えば、生存の結果を伴う臨床試験で、我々は、プラセボ（または標準療法）と比較した新薬の投与を受けた参加者間の生存を比較することに興味があるかもしれません。 観察研究では、我々は男女間、または特定の危険因子（たとえば、高血圧または糖尿病）を持つ参加者と持たない参加者の間で生存を比較することに興味があるかもしれません。
対数順位検定
対数順位検定は、2つ以上の独立したグループの間で生存に差がないという帰無仮説を検定するためによく使われる検定です。 この検定は、グループ間の生存経験全体を比較し、生存曲線が同一（重複）であるかどうかの検定と考えることができます。 生存曲線は、Kaplan-Meier法を用いて、別々に検討された各群について推定され、対数順位検定を用いて統計的に比較される。 様々な統計計算パッケージ（例えば、SAS、R 4,6）で実装されている対数順位検定統計量にはいくつかのバリエーションがあることに注意することが重要である。 ここでは、カイ二乗検定統計量に密接にリンクし、フォローアップ期間中の各時点でのイベントの観察数と期待数を比較する1つのバージョンを紹介します。 試験への参加に同意したステージIVの胃がん患者20名を、手術前に化学療法を行う群と手術後に化学療法を行う群に無作為に割り当てる。 主要評価項目は死亡で、参加者は試験登録後最長48カ月（4年間）追跡されます。 本試験の各アームにおける参加者の体験談は以下の通りです。
|
術前化学療法 |
|
術後化学療法 |
||
|---|---|---|---|---|
|
月齢 死亡 |
最終接触月 |
死亡 |
||
|
8 |
8 |
|
33 |
48 |
|
12 |
32 |
|
28 |
48 |
|
26 |
20 |
|
41 |
25 |
|
14 |
40 |
|
|
37 |
|
21 |
|
|
|
48 |
|
27 |
|
|
|
25 |
|
|
|
|
43 |
|
術前化学療法群では6名が追跡期間中に死亡しており、術前化学療法群では2名が死亡しています。術後化学療法群では3名であった。 各群の他の参加者の追跡期間はさまざまで、48ヵ月で研究が終了するものもある（術後化学療法群）。 上記の手順で、まずKaplan-Meier法を用いて各治療群の生命表を作成する。
手術前に化学療法を受けたグループの生命表
|
Time.Time.Time.Time.Time.Time.Time.Time.Time.Time.Time.Time.Time.Time.Time.Time.Time, ヶ月 |
Number at Risk Nt |
Number of Death Dt |
打ち切り数 Ct |
生存確率
|
|---|---|---|---|---|
|
0 |
10 |
|
|
1 |
|
8 |
10 |
1 |
1 |
0.900 |
|
12 |
8 |
1 |
|
0.788 |
|
14 |
7 |
1 |
|
0.675 |
|
20 |
6 |
|
1 |
0.675 |
|
21 |
5 |
1 |
|
0.540 |
|
26 |
4 |
1 |
|
0.405 |
|
27 |
3 |
1 |
|
0.270 |
|
32 |
2 |
|
1 |
0.270 |
|
40 |
1 |
|
1 |
0.270 |
手術後に化学療法を受けたグループのライフテーブル
|
Time.Time.Time.Time.Time.Time.Time.Time.Time.Time.Time.Time.Time.Time.Time.Time.Time.Time.Time, ヶ月 |
リスクのある数 Nt |
死亡数 Dt |
打ち切り数 Ct |
生存確率
|
|---|---|---|---|---|
|
0 |
10 |
|
|
1 |
|
25 |
10 |
|
2 |
1.000 |
|
28 |
8 |
1 |
|
0.875 |
|
33 |
7 |
1 |
|
0.750 |
|
37 |
6 |
|
1 |
0.750 |
|
41 |
5 |
1 |
|
0.600 |
|
43 |
4 |
|
1 |
0.600 |
|
48 |
3 |
0.600 |
二つの生存曲線は以下の通りである。
各治療群の生存率
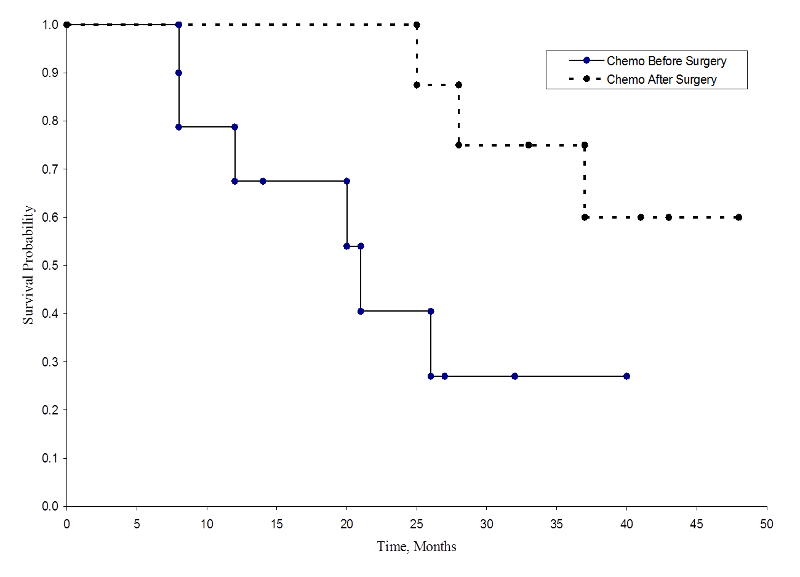
術後化学療法群の生存確率は術前化学療法群の生存確率より高く、生存利益の示唆に富んでいます。 しかし、これらの生存曲線は小さなサンプルから推定されたものである。 群間の生存率を比較するために、対数順位検定を用いることができます。 帰無仮説は、2群間の生存に差がない、またはどの時点でも死亡の確率に集団間の差がない、というものである。 対数順位検定はノンパラメトリック検定で、生存分布について何の仮定も立てない。 本質的に、対数順位検定は、帰無仮説が真である場合（すなわち、.com）に期待されるものと各グループで観察されたイベントの数を比較する。
H0：2つの生存曲線が同一（またはS1t = S2t）対H1：2つの生存曲線が同一ではない（またはS1t ≠ S2t、任意の時間tで）（α=0.05）.
ログ順位統計量はカイ二乗検定統計量として近似分布する(log rank statistics)。 この検定統計量にはいくつかの形式があり、計算の仕方も異なります。 我々は次のものを使う：
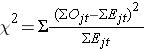
ここでΣOjtはj番目のグループの時間（例えば、j=1，2）にわたるイベントの観察数の合計、ΣEjtはj番目のグループの時間にわたるイベントの期待数の合計を表す。
イベントの観察数と期待数の合計は各イベント時間について計算されて、比較グループごとに合計されている。 対数順位統計量はk-1に等しい自由度を持ち、ここでkは比較群の数を表します。 この例ではk=2なので、検定統計量は自由度1である。
検定統計量を計算するためには、各イベント時間におけるイベントの観察数と期待数が必要である。 イベントの観察数は標本からで、イベントの期待数は帰無仮説が真である（すなわち、生存曲線が同一である）と仮定して計算される。
イベントの期待数を生成するために、イベントが発生したグループにかかわらず、各イベント時間を表す行で生命表にデータを整理する。 また、グループの割り当てを追跡する。 次に、生存率に差がないという仮定（すなわち、帰無仮説が真であると仮定）のもと、両群のデータを合わせて、各時期に発生するイベントの割合（Ot/Nt）を推定する。 これらの推定値に、各比較群のその時点でリスクのある参加者の数（第1群、第2群はそれぞれN1t、N2t）を掛けます。
具体的には、各イベント時間tについて、各群のリスクのある数Njt（例えば、jは群を示し、j=1、2）、各群のイベント（死亡）の数Ojt ,を計算します。 下の表は、上記の生存曲線を比較するために対数順位検定を行うのに必要な情報を含んでいます。 第1群は術前化学療法群、第2群は術後化学療法群を表しています。
生存曲線を比較するためのLog Rank Testのデータ
|
Time.Time.Time.Time.Time.Time.Time.Time.Time.Time.Time.Time.Time.Time, ヶ月 |
第1グループの危険数
N1t |
第2グループの危険数
N2t |
第1グループのイベント数（死亡）
O1t |
グループ数（死亡数 グループ2のイベント（死亡）
O2t |
|---|---|---|---|---|
|
8 |
10 |
1 0 |
||
|
12 |
8 |
10 |
1 |
0 |
|
14 |
7 |
10 |
1 |
0 |
|
21 |
5 |
10 |
1 |
0 |
|
26 |
4 |
8 |
1 |
0 |
|
27 |
3 |
8 |
1 |
0 |
|
28 |
2 |
8 |
0 |
1 |
|
33 |
1 |
7 |
0 |
1 |
|
41 |
0 |
5 |
1 |
次に危険数の合計をします。 各イベント時間におけるNt＝N1t＋N2tと、各イベント時間における観測されたイベント（死亡）数Ot＝O1t＋O2tである。 次に、各グループにおけるイベントの期待数を計算する。 イベントの期待数は各イベント時刻で次のように計算される：
E1t = N1t*(Ot/Nt) for group 1、E2t = N2t*(Ot/Nt) for group 2。 計算結果は下表の通りである。
各グループのイベント数の予想値
|
Time, ヶ月 |
グループ1の危険数 N1t |
グループ2の危険数
N2t |
危険数の合計 Nt |
グループ1のイベント数 O1t |
グループ2のイベント数 O2t |
イベント数合計
Ot |
グループ1 におけるイベント数の期待値 E1t = N1t*(Ot/Nt) |
グループ2 におけるイベント数の期待値 E2t = N2t*(Ot/Nt) |
|---|---|---|---|---|---|---|---|---|
|
8 |
10 |
10 |
20 |
1 |
0 |
1 |
0.500 |
0.500 |
|
12 |
8 |
10 |
18 |
1 |
0 |
1 |
0.444 |
0.556 |
|
14 |
7 |
10 |
17 |
1 |
0 |
1 |
0.412 |
0.588 |
|
21 |
5 |
10 |
15 |
1 |
0 |
1 |
0.333 |
0.667 |
|
26 |
4 |
8 |
12 |
1 |
0 |
1 |
0.333 |
0.667 |
|
27 |
3 |
8 |
11 |
1 |
0 |
1 |
0.273 |
0.727 |
|
28 |
2 |
8 |
10 |
0 |
1 |
1 |
0.200 |
0.800 |
|
33 |
1 |
7 |
8 |
0 |
1 |
1 |
0.125 |
0.875 |
|
41 |
0 |
5 |
5 |
0 |
1 |
1 |
0.000 |
1.000 |
次に、各グループのイベントの観測数（∑O1tとΣO2t）と各グループのイベントの期待数（ΣE1tとΣE2t）を時間的に合計してみる。 これらは次の表の最下段に示されている。
各群の総観測数と期待数
|
Time.Time.Time.Time.Time.Time.Time.Time.Time.Time.Time.Time.Time.Time.Time.Time.Time.Time, 月 |
グループ2の危険数 N2t |
危険数の合計 Nt |
グループ1のイベント数 O1t |
グループ2のイベント数 O2t |
イベント数合計
Ot |
グループ1 におけるイベント数の期待値 E1t = N1t*(Ot/Nt) |
グループ2 におけるイベント数の期待値 E2t = N2t*(Ot/Nt) |
|
|---|---|---|---|---|---|---|---|---|
|
8 |
10 |
10 |
20 |
1 |
0 |
1 |
0.500 |
0.500 |
|
12 |
8 |
10 |
18 |
1 |
0 |
1 |
0.444 |
0.556 |
|
14 |
7 |
10 |
17 |
1 |
0 |
1 |
0.412 |
0.588 |
|
21 |
5 |
10 |
15 |
1 |
0 |
1 |
0.333 |
0.667 |
|
26 |
4 |
8 |
12 |
1 |
0 |
1 |
0.333 |
0.667 |
|
27 |
3 |
8 |
11 |
1 |
0 |
1 |
0.273 |
0.727 |
|
28 |
2 |
8 |
10 |
0 |
1 |
1 |
0.200 |
0.800 |
|
33 |
1 |
7 |
8 |
0 |
1 |
1 |
0.125 |
0.875 |
|
41 |
0 |
5 |
5 |
0 |
1 |
1 |
0.000 |
1.000 |
|
|
6 |
3 |
|
2.620 |
6.380 |
これで検定統計量が計算できる：
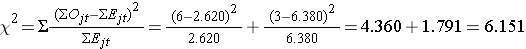
検定統計量は自由度1でカイ二乗として近似分布することがわかる。 したがって、この検定の臨界値は、Χ2分布の臨界値の表で見つけることができます。
この検定では、Χ2 > 3.84 ならH0を棄却するという決定規則があります。 Χ2 = 6.151を観測し、臨界値である3.84を越えている。 したがって、H0を棄却する。 2つの生存曲線が異なることを示すα=0.05の有意な証拠を得た。
例：
ある研究者が、妊娠中のアルコール摂取を防ぐための簡単な介入の有効性を評価したいと考えています。 大量のアルコール摂取の既往がある妊婦が研究に募集され、禁酒に焦点を当てた簡単な介入を受けるか、標準的な出生前ケアを受けるかのいずれかに無作為に割り付けられた。 興味のあるアウトカムは飲酒への再発である。 女性は妊娠約18週で研究に採用され、妊娠の経過から出産（妊娠約39週）まで追跡される。 データは以下の通りであり、女性が飲酒に再発したかどうか、再発した場合は、無作為化からの週数で測定した最初の飲酒の時期を示している。 再発しなかった女性については、無作為化から何週目にアルコールを摂取しなくなったかを記録しています。
|
標準的な出生前ケア |
|
短期介入 |
||
|---|---|---|---|---|
|
再発 |
再発なし |
|
再発なし |
再発なし |
|
19 |
20 |
|
16 |
21 |
|
6 |
19 |
|
21 |
15 |
|
5 |
17 |
|
7 |
18 |
|
4 |
14 |
|
|
18 |
|
|
|
|
||
関心のある質問は、標準の出産前ケアに割り付けられた女性と、短期介入に割り付けられた女性で再発までの時間に差があるかということである。
- Step 1.
仮説を設定し、有意水準を決定する。
H0：再発しない時間はグループ間で同一である vs
H1：再発しない時間はグループ間で同一ではない（α=0.05）
- ステップ 2.
適切な検定統計量を選定する。
対数順位検定の検定統計量は
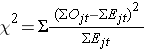
- ステップ3.
決定則の設定
検定統計量はカイ二乗分布に従っているので、Χ2分布の臨界値の表）でdf=k-1=2-1=1、α=0.05のときの臨界値を求めます。 臨界値は3.84であり、決定則はΧ2 > 3.84ならH0を棄却することである。
- Step 4.
検定統計量を計算する
検定統計量を計算するために、イベント（再発）時間に従ってデータを整理し、各処理群におけるリスクのある女性の数、観察された各再発時間に再発する数を決定します。 以下の表で、グループ1は標準的な出生前ケアを受けている女性、グループ2は簡単な介入を受けている女性を表しています。
|
Time, 週数 |
危険数-グループ1 N1t |
危険数-グループ2 N2t |
再発数-グループ1 O1t |
再発数-グループ1 O2t |
|---|---|---|---|---|
|
4 |
8 |
8 1 |
0 |
|
|
5 |
7 |
8 |
1 |
0 |
|
6 |
6 |
7 |
1 |
0 |
|
7 |
5 |
7 |
0 |
1 |
|
16 |
4 |
5 |
0 |
1 |
|
19 |
3 |
2 |
1 |
0 |
|
21 |
0 |
2 |
0 |
1 |
次に危険数の合計を出す。 
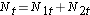、各イベント時間における観察されたイベント（再発）数、
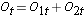、そして
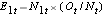と
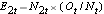を用いて各イベント時間の各グループにおける再発の期待数を決定する。
そして、各群のイベントの観察数（ΣO1tとΣO2t）と各群のイベントの期待数（ΣE1tとΣE2t）を時間的に合計します。 この例のデータに対する計算を以下に示す。
| Time, 週間 |
リスクグループ1の数 N1t |
リスクグループ2の数 N2t |
リスクのある総数 Nt |
再発回数 グループ1 O1t |
再発回数 グループ2 O2t |
総再発回数 Ot |
グループ1の再発予想数
|
グループ2の再発予想数
|
|---|---|---|---|---|---|---|---|---|
|
4 |
8 |
8 |
16 |
1 |
0 |
1 |
0.500 |
0.500 |
|
5 |
7 |
8 |
15 |
1 |
0 |
1 |
0.467 |
0.533 |
|
6 |
6 |
7 |
13 |
1 |
0 |
1 |
0.462 |
0.538 |
|
7 |
5 |
7 |
12 |
0 |
1 |
1 |
0.417 |
0.583 |
|
16 |
4 |
5 |
9 |
0 |
1 |
1 |
0.444 |
0.556 |
|
19 |
3 |
2 |
5 |
1 |
0 |
1 |
0.600 |
0.400 |
|
21 |
0 |
2 |
2 |
0 |
1 |
1 |
0.000 |
1.000 |
|
|
|
|
|
4 |
3 |
|
2.890 |
4.110 |
ここで検定統計量を計算する：
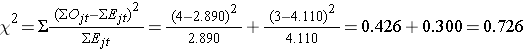
- Step 5.
結論。 0.726 < 3.84なので、H0を棄却しない。 α=0.05で、再発までの時間が群間で異なることを示す統計的に有意な証拠はない
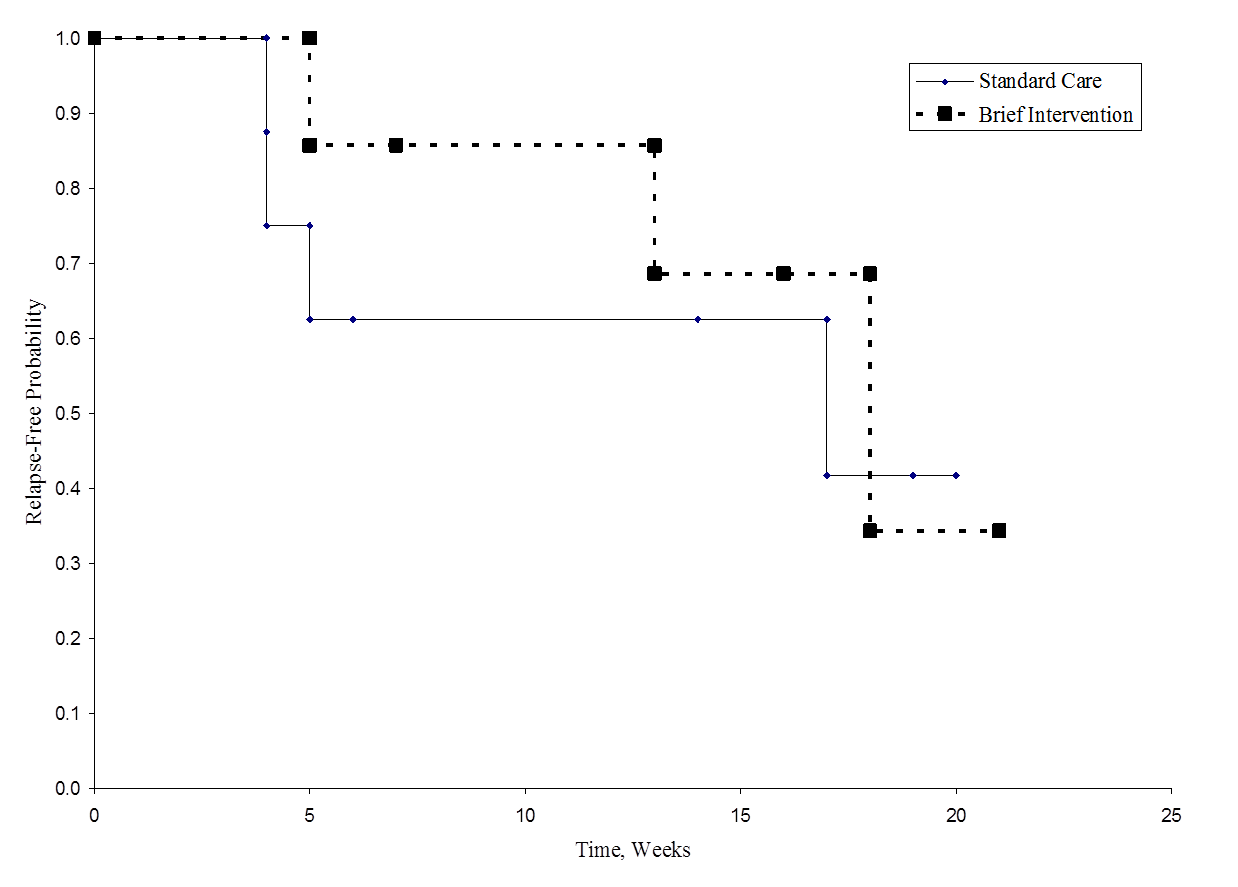
下図は、各群の生存期間（無再発時間）を示しています。 生存曲線はあまり分離していないことに注目し、仮説の検定で有意でない結果と一致しています。
Relapse-Free Time in Each Group
前述のようにlog rank statisticにはいくつかのバリエーションが存在します。 いくつかの統計計算パッケージは、2つの独立したグループを比較するための対数順位検定に次の検定統計量を使用します：
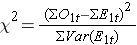
ここでΣO1tはグループ1におけるイベントの観察数の合計、ΣE1tはすべてのイベント時間にわたって取ったグループ1のイベントの期待数の合計である。 分母は各イベント時間でのイベントの期待数の分散の合計で、これは次のように計算されます：
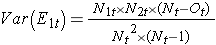
独立グループ間の生存関数を比較する他の検定と同様に対数順位統計の他のバージョンもあります7-9。 例えば、よく使われる検定に修正Wilcoxon検定があり、これはフォローアップの後半とは対照的に、初期のハザードにおける大きな差に敏感である10
先頭に戻る｜前のページ｜次のページ
に戻る