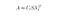Hello Folks! 今回は、自然言語処理で使われるアルゴリズムについて説明します。
このメソッドの主な用途は、言語学において多岐にわたります。 低次元空間における文書の比較（Document Similarity）、文書間で繰り返されるトピックの発見（Topic Modeling）、用語間の関係の発見（Text Synoymity）。

Introduction

潜在的意味解析モデルは、意味
表現が、それがどのように構造化されているかについて明確な指示なしに言語の大きなサンプルに遭遇することからどのように学習されるかもしれないという理論である。
手元の問題は教師なし、つまり、コーパスに割り当てられた固定ラベルやカテゴリを持っていません。

ドキュメントからパターンを抽出し理解するために、LSA は本質的にある仮定に従っています：
1) 文やドキュメントの意味は、その中に現れるすべての単語の意味の合計である。 全体として、ある単語の意味は、それが出現するすべての文書にわたる平均である。
2) LSA は、単語間の意味的な関連付けは、明示的にではなく、言語の大きなサンプルに潜在的にのみ存在すると仮定する。

Mathematical Perspective

Latent Semantic Analysis（LSA）は、文書に関する洞察を得るための特定の数学演算からなる。 このアルゴリズムは、トピック モデリングの基礎を形成しています。 コアとなる考え方は、ドキュメントと用語という今あるものの行列を取り、それを個別のドキュメント-トピック行列とトピック-用語行列に分解することである。
m個の文書とn個の単語があるとすると、
m×nの行列Aを構成することができます。この行列は各行が文書を表し、各列が単語を表します。

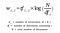
直観的に、ある単語は文書中では頻繁に出現するがコーパスはあまり出現しないと大きな重みを持っていることがわかる。
この変換方法(tf-IDF)を用いて文書-用語行列Aを作り、コーパスをベクトル化する。 (我々はまだ文字列を扱っていないので、我々のモデルが処理・評価できるような方法で！）。
しかし、微妙な欠点があります。それは、Aはノイズが多く、疎な行列なので、Aを観測しても何も推測できないことです。 (5389>

Topic Modeling は本質的に教師なしアルゴリズムであるため、潜在的なトピックを事前に特定する必要があります。 この場合、Truncated Singular Value Decomposition (SVD) を使用した次元削減技術を使用して低ランク近似を実行します。 M=U*S*V, S は M の特異値を表す対角行列。

Truncated SVD は、最大の特異値 t 個だけを選択し、U と V の最初の t 列だけを残して、次元を減らします。 この場合、tは見つけたいトピックの数を反映して選択・調整できるハイパーパラメータである。

注：Truncated SVDは次元削減であって、SVDではない！

注：SVDは次元削減ではない！

注：SVDは次元削減ではない。

これらの文書ベクトルと項ベクトルを使って、コサイン類似度などの評価手段を簡単に適用できるようになりました。

• 異なる文書の類似性
• 異なる単語の類似性
• 用語（または「クエリー」）と文書の類似性（これは情報検索で、検索クエリーに最も関連する文章を取得したいときに有用である）を評価するために、コサイン類似度のような尺度を簡単に適用できる。

最後に、

このアルゴリズムは、さまざまな NLP ベースのタスクで主に使用されており、確率的 LSA や潜在的ディリクレ配分法 (LDA) などのより堅牢なメソッドの基礎となっています。