アイスクリームでは、ソフトでクリーミーな食感を出すために、小さな丸い氷の結晶が重要です。 一般に、凍結速度が速いほど氷の結晶の大きさは小さくなると言われています。 しかし、食品素材によっては、凍結速度に上限があるものもあります。 凍結速度が速すぎると、食品素材に機械的なストレスがかかり、凍結破壊が起こる可能性がある。 また、日本の伝統的な料理であるこり豆腐や、生体組織工学で用いられる足場材など、凍結を利用して材料が構造化される場合も少なくない。 数年前、WURはデルフト工科大学およびユニリーバと共同で、スープ野菜の構造化にフリーズドライを使用することを研究しました。

氷の結晶サイズと凍結速度の関係

したがって、冷凍食品の品質の観点からは、氷の結晶サイズと凍結速度の関係についてよく知ることが重要である。 しかし，凍結速度と氷結晶の大きさとの間には，経験的な関係がいくつか存在するのみである． また，製造された食品には，糖類などの凍結防止剤や凍結防止蛋白質など，氷結晶の大きさを制御するための手段が用いられている． このことから、食品素材の組成と凍結速度、氷晶サイズの間には相互作用があると予想されますが、経験則では食品組成への依存性はありません。 そこで、食品 & バイオベース研究部門は、高度なコンピュータ・シミュレーションを用いて、凍結速度、組成、氷晶サイズの関係をより理論的に理解することを目的とした研究プロジェクトに取り組みました。 この分野の最先端の手法はフェーズフィールドモデルで、乳化剤で安定化されたフォームやエマルションのような分散体の構造を記述するために利用しています。 フェーズフィールド法では、エマルション液滴、フォームバブル、結晶など、分散体の複数の個別要素を同時にモデル化することができます。 この手法では、これらの分散要素の分解と合体を容易に行うことができる。

この手法の強みは、分散相と連続相の間の界面をどのように扱うかにある。 ここでは、オランダの有名な物理学者であるvanderWaalsの提案に従って、熱力学的な枠組みに界面を含める方法をとっている。 私たちは、このフェーズフィールド法を用いて、ショ糖水溶液中の氷晶を記述するコンピュータモデルを構築しました。このモデルは、アイスクリームを代表する挙動と見なすことができます3。 私たちはこれまでの研究で、ショ糖水溶液の熱力学4と、拡散による糖液中の水分移動の速度5を明らかにしてきました。

凍結速度、組成、氷結晶サイズ

計算機モデルを開発した後、いくつかの計算機シミュレーションを行い、凍結速度、組成、氷結晶サイズの関係について検討した。 食品材料の小さな部分にズームインして、氷の結晶が成長するための核をいくつか蒔いた。 そして、この食品素材の一部に、さまざまな凍結速度を適用した。 シミュレーションは2種類のショ糖濃度、および核のランダムな位置の違いについて行い、良い統計値を得ることができました

これらのコンピュータシミュレーションのスナップショットを図1に示します。 濃い青色に分散しているのは個々の氷の結晶である。 凍結速度はそれほど速くないので、氷の結晶はほぼ球状を保っていると考えてよい。 シミュレーション結果を理解する上で重要なことは、氷の結晶には糖分が含まれていないことで、氷の結晶が成長するということは、未凍結相の糖分濃度が上昇することを意味する。

図1: 異なる凝固速度（上から0.01、0.03、0.10K/s）のコンピュータシミュレーションによって得られた、異なる時間（左から右）に観察された砂糖溶液中の氷結晶成長のスナップショット。 特に凝固速度が低い場合（上）、複数の氷晶が合体しているのがわかる。

さらに凝固すると、氷晶同士が衝突し、その間の未凝固液の糖濃度が上昇し、凝固点降下に至ることがある。 その結果、平坦な界面が形成される。 凍結速度が遅いと、糖が衝突領域から拡散する時間があり、結晶が合体することがある。 氷晶成長による糖の局所的な濃度上昇が小さい凍結初期には、数回の合体現象が見られる。

シミュレーションから平均氷結晶サイズを決定し、2種類のショ糖濃度に対して課した凍結速度に対してプロットしました。 核生成過程の確率のため、シミュレーションデータにはかなりのばらつきが観察される。 しかし、多くのシミュレーションを実行することによって、信頼性の高いべき乗則の関係をデータに当てはめることができるようになった。 このフィッティングにより、初期糖度10%と15%の場合のべき乗則の指数は、それぞれ0.31と0.18であることがわかります。 私たちの以前の経験的関係は、べき乗則の指数が0.25であり、これは組成に依存しないと仮定されていた。 この経験則の値が、シミュレーションによって得られた指数にかなり近いという事実は、非常に心強いものです。 さらに、すべての材料と熱力学的特性が既知であるため、シミュレーションモデルにパラメータフィッティングが必要なかったことも特筆されます。

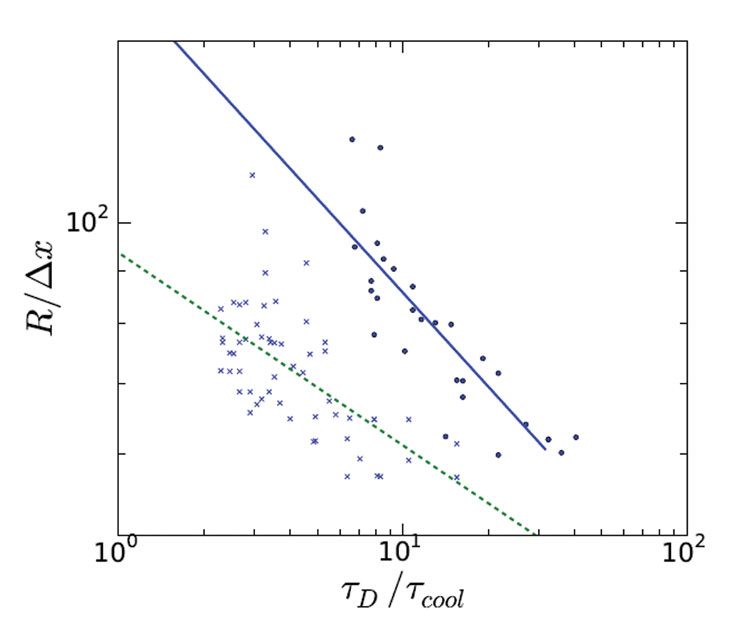
図2：2種類の初期糖濃度（10％と15％、実線と破線で示す）の氷結晶サイズと凍結速度の関係を示す。 半径は計算メッシュの単位である約3ミクロン、凍結速度1/tcoolは水の拡散速度1/tDで測定したものである。 (tD/tcool=1の場合は0.01K/sで) 点は1回のシミュレーションの平均的な大きさを示している。 線はシミュレーションデータに当てはめたべき乗則の関係

Food quality issues for frozen fruits and vegetables

Food & Biobased Researchは、このモデルが大きな現実性を持っていると結論付けています。 さらに、材料と熱力学的特性に関する同様の予測理論が、他の多くの食品材料についても利用可能です。 したがって、このモデルは原理的には他の多くの食品素材に適用可能です。 これを基に、我々は、果物や野菜の冷凍食品の品質問題を調査するために、細胞構造を持つ冷凍食品材料にこのモデルを適用し、開発を続ける新しい研究プロジェクトを立ち上げました。 位相場モデルはマルチスケールモデルに組み込まれる予定です。食品では凍結速度の局所的な違いが生じるため、製品スケールで温度プロファイルを計算し、マイクロスケールで氷結晶成長を計算するという高度なアプローチで解決する必要があるからです。 マクロスケールコンピュータモデルは、マイクロスケールモデルを多くの場所について何度も呼び出します。 マイクロスケールモデルは局所的な氷の割合を報告し、マクロスケールモデルは適用された温度勾配をマイクロスケールモデルに伝えます。

この新しいプロジェクト「食品 & バイオベース研究」では、最初の冷凍段階だけではなく、冷凍保存にも焦点を当てます。 保存中は機械的な冷却やドアの開閉などにより、温度変動が起こります。 このような温度変動により、氷の結晶がさらに成長し、製品の品質が損なわれることが想定される6。 そこで、保存温度を下げることで、温度変化の影響を受けにくくなり、さらにはエネルギー使用量の削減が可能かどうかを調査することを目的としています。 また、保存温度がある程度一定でも、従来の-18℃の条件では保存中に氷の結晶分布の粗密が発生することがある。 これは、エアブラスト凍結とPSF（Pressure Shift Freezing）凍結の比較で示されています。 PSFは従来のエアブラスト凍結に比べ、初期には氷結晶の大きさが非常に小さくなっています。 しかし、数週間の保存後、最終的な氷結晶サイズ分布にはほとんど差が見られず、PSF食品の保存中に粗大化が起こったことが示されました7。 処方と加工が冷凍食品の品質に与える影響を知ることで、製品品質と省エネの両方への影響から、冷凍保存の新しい戦略を評価することができます。

1. Voda, A., Homan, N., Witek, M., Duijster, A., van Dalen, G., van der Sman, R., Nijsse, J, van Vliet, L. Van As, H. & van Duynhoven, J. (2012). ニンジンの微細構造および補水性に及ぼす凍結乾燥の影響。 Food Research International, 49(2), 687-693
2. van der Sman, R. G. M., Voda, A., van Dalen, G., & Duijster, A. (2013).を参照。 冷凍食品における氷晶のインタースペーシング Journal of Food Engineering, 116(2), 622-626
3. van der Sman, R. G. M. (2016).。 糖質溶液における氷結晶成長の位相場シミュレーション． International Journal of Heat and Mass Transfer, 95, 153-161
4. van der Sman, R. G. M., & Meinders, M. B. J. (2011).を参照。 Flory-Huggins自由体積理論によるデンプン水混合物の状態図の予測。 Soft Matter, 7(2), 429-442
5. van der Sman, R. G. M., & Meinders, M. B. J. (2013)。 食品素材における水分の拡散性. Food chemistry, 138(2), 1265-1274
6. Regand, A &Goff HD. “冷凍安定化アイスクリームモデル系における構造と氷の再結晶化”. Food Hydrocolloids1 (2003): 95-102
7. Fernández PP, Otero L, Martino MM ,Molina-García AD, & Sanz PD “High-pressure shift freezing: recrystallization during storage” European Food Research and Technology 5 (2008): 1367-1377

著者について

Ruud van der Smanはデルフト工科大学で応用物理学の修士号を、ワーヘニンゲン大学で農業工学の博士号を取得しています。 ワーヘニンゲンUR（大学&研究センター）の食品&バイオベース研究所の上級研究員、食品プロセス工学の非常勤助教授として勤務している。 研究テーマは、食品材料のソフトマター物理学、マイクロメートルスケールの食品構造のコンピュータモデリング、および生理学のモデリングである。 食肉に関する専門知識は、保水力、熱および物質移動、死後生理学の熱力学から構成されています。www.wageningenur.nl/en/fbr