電磁メタマテリアルは、波長よりも小さいその構造的特徴に衝突するか、またはそれと相互作用する電磁波に影響を与えます。 有効屈折率によって正確に記述される均質な材料として動作するために、その特徴は波長よりもはるかに小さくなければなりません。
マイクロ波放射については、特徴はミリメートルのオーダーになります。 マイクロ波周波数メタマテリアルは、通常、適切な誘導性および容量特性を持つ導電性要素(ループ状のワイヤなど)のアレイとして構築されます。 多くのマイクロ波メタマテリアルは、スプリットリング共振器を使用しています。
フォトニックメタマテリアルは、ナノメートル単位で構造化され、光周波数で光を操作します。 フォトニック結晶や、回折格子、誘電体ミラー、光学コーティングなどの周波数選択的な表面は、サブ波長構造メタマテリアルと類似性を示している。 しかし、これらの機能は回折や干渉から生じるため、均質な物質として近似できないことから、通常、メタマテリアルとは区別して考えられている。 しかし、フォトニック結晶のような物質構造は、可視光領域で有効である。 可視光域の中間の波長は約560nm(太陽光の場合)。
プラズモン メタマテリアルは、金属の表面で光周波数で集団的に振動する電荷の塊である表面プラズモンを利用します。
周波数選択性表面 (FSS) はサブ波長特性を示すことができ、人工磁気導体 (AMC) または高インピーダンス表面 (HIS) としてさまざまな形で知られています。 FSSは、そのサブ波長構造に直接関係する誘導性および容量性特性を示す。
電磁メタマテリアルは、以下のようにさまざまなクラスに分類されます:
負の屈折率編集
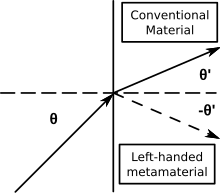
負指数メタマテリアル(NIM)は、負の屈折率によって特徴づけられる。 NIMの他の用語には、「左巻き媒体」、「負の屈折率を有する媒体」、「後方波媒体」などがある。 負の屈折率が負の誘電率と負の透磁率から同時に生じるNIMは、ダブルネガティブメタマテリアルまたはダブルネガティブ材料(DNG)とも呼ばれる。
実数の誘電率と透磁率でよく近似された材料を仮定すると、誘電率ϵ r {\displaystyle \epsilon _{r}} の関係は、次のようになる。

, 透磁率μr {displaystyle \mu _{r}}.

屈折率 n は n = ± ϵ r μ r {displaystyle \scriptstyle n=pm {}sqrt {epsilon _{Àmathrm {r}} で与えられます。 }mu _{mathrm {r}. }}}}

. メタマテリアル以外の透明材料(ガラス、水、…)はすべて正のr { {displaystyle \epsilon _{r}} を持つ。

and μ r {displaystyle \mu _{r}} {4777>
. ただし、一部のメタマテリアルでは、ϵ r { {displaystyle \epsilon _{r}}} が正の平方根になるように設計されています。

and μ r < 0 {displaystyle \mu _{r}<0}

。 なぜなら、積 ϵ r μ r {displaystyle \epsilon _{r}mu _{r}} は、次のようになるからです。

is positive, n is real. このような状況では、nに対して負の平方根をとる必要がある。

and μ r {displaystyle \mu _{r}}}

が正(負)の場合、波は順方向(逆方向)に進むことになります。 r {displaystyle \epsilon _{r}} の物質中では電磁波は伝搬しない。

and μ r {displaystyle \mu _{r}} {4777>
以上の考察は実際の材料では単純で、複素数の ϵ r {displaystyle \epsilon _{r}} を持っていなければいけません。

and μ r {displaystyle \mu _{r}} {4777>

and μ r {displaystyle \mu _{r}}.

は負の屈折を示す受動物質である必要はない。 実際、円偏波に対する負の屈折率は、キラリティーから生じることもある。 負のnを有するメタマテリアルは、多数の興味深い特性を有する。
- スネルの法則(n1sinθ1 = n2sinθ2)はまだ屈折を記述しますが、n2が負なので、正と負の指数材料の界面で入射と屈折光線が表面法線の同じ側にあるのです。
- 時間平均したポインティングベクトルは位相速度と逆平行である。 しかし、波(エネルギー)が伝播するためには、物質パラメータの波数依存性を満たすために、-μと-εが対になっていなければならない k c = ω μ ϵ {displaystyle kc=omega { }sqrt {}mu \epsilon }} {} {}。
.
負の屈折率は数学的にはベクトルの三つ組E、H、kから導かれる。
電磁メタマテリアル中を伝播する平面波に対して電界、磁界、波のベクトルは従来の光学物質の挙動とは逆に左手の法則に従っている。
現在までに、負の屈折率を示すのはメタマテリアルだけです。
Single negative 編集
シングルネガティブ(SNG)メタマテリアルは負の比誘電率(εr)または負の比透磁率(μr)を持ちますが、両方ではありません。
Epsilon negative media (ENG)は、εrが負でµrが正である。 多くのプラズマがこの性質を持つ。 例えば、金や銀などの貴金属は赤外や可視域でENGとなる。
Mu-negative media (MNG) は正のεrと負のµrを示す。 ジャイロトロピックあるいはジャイロマグネティックな物質がこの性質を示す。 ジャイロトロピック材料とは、準静的磁場の存在によって変化し、磁気光学効果を可能にした材料である。 磁気光学効果とは、このような媒質中を電磁波が伝搬する現象である。 このような物質では、左回転楕円偏波と右回転楕円偏波が異なる速度で伝搬することができる。 磁気光学物質の層を光が透過すると、偏光面が回転してファラデー回転子を形成することができ、これをファラデー効果と呼ぶ。 このような反射の結果は、磁気光学カー効果として知られている(非線形カー効果とは混同しないように)。 2つの主偏光の回転方向を逆にした2つのジャイロトロピック材料を光学異性体と呼ぶ。
ENG材料のスラブとMNG材料のスラブを接合すると、共鳴、異常トンネル、透明、ゼロ反射などの性質が得られた。
HyperbolicEdit
双曲線メタマテリアル(HMM)は、ある偏光や光の伝搬方向に対しては金属として振る舞い、それ以外に対しては負と正の誘電率テンソル成分により誘電体として振る舞い、極めて異方性を与えるものである。 この物質の波動ベクトル空間での分散関係は双曲面を形成するため、双曲面メタマテリアルと呼ばれる。 HMMの極端な異方性により、光の伝播が内部および表面で指向性を持つようになる。
BandgapEdit
電磁バンドギャップメタマテリアル(EBGまたはEBM)は、光の伝搬を制御します。 これは、フォトニック結晶(PC)または左手系材料(LHM)で実現される。 PCは光の伝搬を完全に禁止することができる。 どちらも、特定の方向への光の伝播が可能で、希望する周波数にバンドギャップがあるように設計することができます。 EBG の周期サイズは波長のかなりの割合であり、建設的および破壊的干渉を引き起こします。
PC は、その特性がバンドギャップ特性から得られるため、波長可変メタマテリアルのようなサブ波長構造とは区別されます。 PCは、サブ波長構造を露出させる他のメタマテリアルに対して、光の波長に一致するサイズである。 さらに、PCは光を回折させることで機能する。 3174>
PC には周期的な包有物があり、その包有物が散乱による破壊的干渉を起こすことで波の伝搬を抑制している。 PCのフォトニックバンドギャップ特性は、PCを電子半導体結晶の電磁アナログにする。
EBG は、高品質で低損失の周期的な誘電体構造を作成することを目的としている。 EBG は、半導体材料が電子に影響を与えるのと同じように、光子に影響を与えます。 PC は光の伝搬を許さないため、完璧なバンドギャップ材料と言えます。
EBGは、特定の到来角と偏光に対して、割り当てられた周波数帯域の伝搬を阻止するように設計されています。 EBGの特殊な特性を実現するために、さまざまな形状や構造が提案されている。 数ギガヘルツから数テラヘルツの周波数帯、ラジオ、マイクロ波、中赤外の周波数帯で製造されている。 EBGの応用開発には、伝送線路、誘電体の角棒でできたウッドパイル、数種類の低利得アンテナなどがある。
Double positive mediumEdit
DPS (Double positive medium) は、天然由来の誘電体など、自然界にも存在する。 誘電率と透磁率がともに正であり、波の伝搬は順方向である。 DPS、ENG、MNGの特性を兼ね備えた人工材料が作製されている。
Bi-isotropic and bianisotropicEdit
メタマテリアルをダブルあるいはシングルネガティブ、ダブルポジティブに分類すると、通常はメタマテリアルがεとμで表される独立した電気および磁気応答を持つと仮定される。 このような媒体を「二等方性」と呼ぶ。
二等方性媒体の磁気電気結合には、4つの材料パラメータが内在しています。 それらは電界強度(E)と磁界強度(H)、電荷密度(D)と磁束密度(B)である。 これらのパラメータはそれぞれ、ε、μ、κ、χ、または誘電率、透磁率、カイラリティの強さ、テレゲンパラメータである。 この種の媒体では、材料パラメータは回転した測定座標系に沿って変化することはない。 この意味で、それらは不変またはスカラーである。
固有磁性パラメータであるκおよびχは、波の位相に影響を与える。 キラリティパラメータの効果は屈折率を分割することである。 等方性媒質では、εとµが同じ符号を持つ場合にのみ、波の伝搬がこの結果となります。 χをゼロと仮定し、κをゼロ以外の値とした二等方性媒質では、異なる結果が現れます。 後方波または前方波のいずれかが発生する可能性があります。
一般に、双異方性材料の構成式はD = ϵ E + ξ H , { {displaystyle \mathbf {D} =epsilon \mathbf {E}} となる。 +xi \mathbf {H} ,}

B = ζ E + μ H , {}displaystyle \mathbf {B} = Neitherzeta \mathbf {E}. +mu \mathbf {H} ,}
where ϵ {displaystyle \epsilon }.

and μ {displaystyle \mu } }.

はそれぞれ誘電率、透磁率テンソル、ξ {displaystyle \xi }は誘電率、透磁率テンソルです。

とζ{displaystyle \zeta }の2つです。

は2つの磁電テンソルである。 媒質が逆数の場合、誘電率と透磁率は対称テンソルであり、ξ = – ζ T = – i κ T {displaystyle \xi =-πzeta ^{T}=-πkappa ^{T}} となる。

, where κ {displaystyle \kappa } 가능합니다.

はキラルな電磁気的、逆磁気電気的応答を記述するキラルテンソルである。 キラルテンソルは、κ = 1 3 tr ( κ ) I + N + J {displaystyle \kappa ={}tfrac {1}{3}} {operatorname {tr}} で表される。 (\kappa )I+N+J}。

, where tr ( κ ) {displaystyle \operatorname {tr}. (┳┳)┳┳。}

は κ {displaystyle \kappa } のトレースです。

, I は単位行列、N は対称なトレースフリーテンソル、Jは反対称なテンソルである。 このような分解により、逆バイアス応答を分類することができ、以下の3つの主要なクラスを確認することができる。 (i) キラル媒体( tr ( κ ) ≠ 0 , N ≠ 0 , J = 0 {displaystyle \operatorname {tr} } }. (\kappa )\neq 0,Nneq 0,J=0}.

), (ii) pseudochiral media ( tr ( κ ) = 0 , N ≠ 0 , J = 0 {displaystyle \operatorname {tr} ]擬似キラル媒体 (\kappa )=0,Nneq 0,J=0}.

), (iii) omega media ( tr ( κ ) = 0 , N = 0 , J ≠ 0 {displaystyle \operatorname {tr} ). (\kappa )=0,N=0,Jneq 0}

).
ChiralEdit
メタマテリアルの文献には、左利きと右利きの用語の2つの矛盾した使い方が含まれているため、メタマテリアルの手の大きさは、混乱の原因となる可能性があります。 1つは、キラル媒体の伝搬モードである2つの円偏波のうちの1つを指します。 2つ目は、ほとんどの場合キラルではない負の屈折率媒質で生じる電場、磁場、ポインティングベクトルの三つ組に関連する。
一般にキラルおよび/または双等性の電磁応答は、3次元幾何学キラリティの結果である。 2次元キラリティーという概念も存在し、平面上の物体を平面から持ち上げないと鏡像に重ね合わせることができない場合、キラリティーという。 異方的で損失の大きい2次元キラルメタマテリアルは、円形変換二色性により円偏波の方向非対称な透過(反射、吸収)を示すことが確認されている。 一方、2次元でも3次元でもない幾何学的なアキラル構造からは、双等方的な応答が生じることがある。 Plumらは、放射波動ベクトルとともに(アキラル)構造の配置がその鏡像と異なる外部キラリティーによる磁電結合を調べ、大きく調整可能な線形光学活性、非線形光学活性、鏡面光学活性、円形変換二色性を観測した。 Rizzaらは、幾何学的に一次元キラルであれば実効キラルテンソルが消失しない(回転を伴わない並進では構造全体の鏡像が重ねられない)1次元キラメタマテリアルを提案した
3次元キラメタマテリアルは、実効キラリティパラメータκ {displaystyle \kappa }がキラル材料または共振器から構成されている。

は0でない。 このようなキラルメタマテリアルにおける波動伝播特性は、強いキラリティと正の r {displaystyle \epsilon _{r}} を持つメタマテリアルで負の屈折が実現できることを示している。

and μ r {displaystyle \mu _{r}} {6611>

. これは、屈折率n { {displaystyle n} が

は左右の円偏波に対して異なる値を持ち、
n = ± ϵ r μ r ± κ {displaystyle n=pm {}sqrt {}epsilon _{r}mu _{r}}}pm \kappa } によって表される。

κ {displaystyle \kappa }が1偏波で負の指数となることがわかる。

> ϵ r μ r {displaystyle {sqrt {epsilon _{r} ◇mu _{r}}}}

. この場合、ϵ r {displaystyle \epsilon _{r}} のどちらか、または両方が必要なわけではありません。

and μ r { 쇼displaystyle \mu _{r}}}.

は後方波動伝播のため負の値である。 キラリティーによる負の屈折率は、2009年にPlumらとZhangらによって同時かつ独立に初めて観測された。
FSS basedEdit
周波数選択性表面ベースメタマテリアルは、ある波長帯の信号をブロックし、別の波長帯の信号を通過させる。 固定周波数メタマテリアルの代替品として注目されている。 固定周波数応答の制限ではなく、1つの媒体で周波数を任意に変更することができます。
