
Dans cet article, je vais présenter les bases du maintien de la qualité.
Cela implique l’assurance qualité, le contrôle qualité et la métrologie. Nous utilisons l’assurance qualité pour avoir la certitude que les exigences de qualité seront satisfaites. Le contrôle de la qualité est utilisé pour vérifier que les exigences ont été remplies. Il s’agit d’une différence subtile et, dans la pratique, les termes sont parfois utilisés de manière interchangeable. La métrologie est la science de la mesure. C’est la façon dont nous nous assurons que nous pouvons comparer en toute confiance les résultats des mesures effectuées dans le monde entier.
Ces principes peuvent s’appliquer à des produits ou à un service, mais je vais me concentrer sur la fabrication et sur la façon dont ces trois concepts fondamentaux sont liés les uns aux autres dans ce contexte. J’ai donc évité les détails des méthodes spécifiques et je n’entre pas dans les mathématiques. Je garderai cela pour un article ultérieur.
Origines de la mesure
Les Égyptiens utilisaient des étalons de mesure, avec des calibrages réguliers, pour s’assurer que les pierres s’emboîteraient les unes dans les autres dans leurs grands projets de construction. Mais les systèmes de qualité modernes ont vraiment commencé pendant la révolution industrielle. Auparavant, les biens mécaniques étaient construits par des artisans qui ajustaient chaque pièce individuellement pour qu’elle s’intègre dans un ensemble. Cela signifie que chaque machine, et chaque pièce qui la compose, était unique. Si une pièce devait être remplacée, alors un artisan devait monter une nouvelle pièce.
A la fin du 18 ème siècle, les fabricants d’armes français ont commencé à fabriquer des mousquets avec des pièces standard. Cela signifiait que l’armée pouvait transporter des pièces de rechange et les échanger rapidement contre des pièces cassées. Ces pièces interchangeables étaient encore ébarbées pour s’adapter à l’assemblage mais au lieu d’adapter chaque pièce à l’arme individuelle, elle était adaptée à une pièce maîtresse .
Quelques années plus tard, les armuriers américains ont commencé à utiliser cette méthode mais l’ont adaptée à leurs ouvriers non formés. Ils déposaient des calibres pour s’adapter à la pièce maîtresse, les ouvriers réglaient les gabarits et les machines de production en utilisant les calibres, et utilisaient également les calibres pour vérifier les pièces. Cela permettait à une rangée de machines, chacune effectuant une seule opération avec un opérateur non qualifié, de produire des pièces précises. Ces pièces pouvaient ensuite être rapidement assemblées en machines complexes.
Les bases de la fabrication moderne avaient ainsi été posées, plus de 100 ans avant que Ford n’applique ces idées à une ligne de production en mouvement.
Calibrage, valeur réelle et erreur de mesure
Un système de pièces maîtresses, de jauges et de machines à usage unique fonctionnait lorsqu’un produit entier était fabriqué dans une seule usine. Les chaînes d’approvisionnement mondiales modernes ont besoin d’un système différent.
Au lieu d’avoir une pièce maîtresse physique, nous avons un dessin ou un modèle CAO numérique. Les tolérances spécifiées garantissent que les pièces s’emboîteront et fonctionneront comme prévu. Au lieu que chaque fabricant vienne à une pièce maîtresse unique pour régler ses jauges, ils font étalonner leurs instruments de mesure. Ces instruments sont ensuite utilisés pour régler les machines de production et pour contrôler les pièces produites.
Toute la qualité dépend de ce processus d’étalonnage.
Le concept le plus important à comprendre est que toutes les mesures ont une incertitude. Si je vous demandais d’estimer la hauteur de ce texte, vous pourriez dire, ‘ c’est environ 4 mm’ . L’utilisation du mot ‘environ’ implique qu’il y a une certaine incertitude dans votre estimation.
En fait, nous ne pouvons jamais connaître la vraie valeur exacte de quoi que ce soit, toutes les mesures sont en fait des estimations, et présentent une certaine incertitude. La différence entre le résultat d’une mesure et la vraie valeur est l’erreur de mesure . Puisque nous ne pouvons pas connaître la vraie valeur, nous ne pouvons pas non plus connaître l’erreur : ce sont des quantités inconnaissables.
Tout ce que nous pouvons quantifier sur le monde qui nous entoure, ce sont les résultats des mesures et celles-ci comportent toujours une certaine incertitude, même si cette incertitude est très faible.
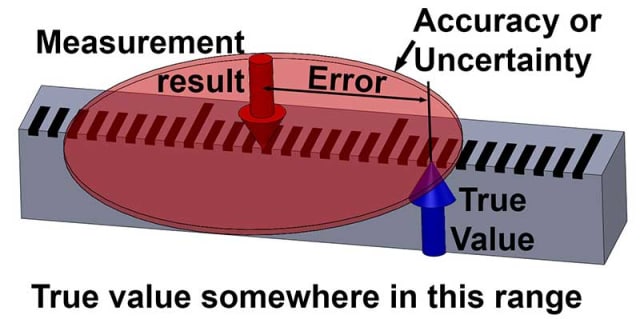
Si vous deviez estimer la hauteur de ce texte à ‘ environ 4 mm, à 1 mm près’, alors vous avez maintenant attribué certaines limites à votre incertitude. Mais vous ne pouvez toujours pas être sûr à 100% que c’est vrai.
Vous pourriez avoir un certain niveau de confiance, disons 95 pour cent, que c’est vrai. Si vous augmentez les limites, à 2 mm près, alors votre confiance augmentera, peut-être jusqu’à 99%. Donc l’incertitude donne certaines limites dans lesquelles nous avons un niveau de confiance que la vraie valeur se trouve.
OK, le cours de philosophie est terminé !
Dans un prochain billet, je développerai ces idées et comment on peut calculer l’incertitude pour un niveau de confiance particulier.
Incertitude et qualité
Une fois que nous avons déterminé l’incertitude (ou « précision ») d’une mesure, nous pouvons ensuite l’appliquer pour décider si une pièce est conforme à une tolérance spécifiée. Par exemple, disons qu’une pièce est spécifiée comme devant être de 100 mm +/- 1 mm. Nous la mesurons et obtenons un résultat de 100,87 mm.
La pièce est-elle conforme aux spécifications ?
La réponse simple est : « Nous ne savons pas, peut-être qu’elle l’est, mais peut-être qu’il y a eu une erreur dans notre mesure et qu’en fait la pièce fait plus de 101 mm. Peut-être qu’il y a eu une erreur encore plus grande et que la pièce est en fait inférieure à 99 mm ! ».
A moins de savoir quelle est l’incertitude de la mesure, nous n’avons aucune idée de la confiance que nous pouvons avoir dans le fait que la pièce est conforme aux spécifications. Supposons que l’incertitude de la mesure ait été donnée de sorte que le résultat de la mesure soit de 100,87 mm +/- 0,1 mm avec une confiance de 95 %. Maintenant, nous pouvons dire avec plus de 95 % de confiance que la pièce est conforme aux spécifications.
Donc, comprendre et quantifier l’incertitude des mesures est essentiel pour maintenir la qualité.
Maintenant, considérons l’étalonnage et le concept associé de traçabilité. C’est un aspect fondamental de l’incertitude. Un étalonnage est une comparaison avec une référence, et l’incertitude de cette comparaison doit toujours être incluse, pour les raisons expliquées ci-dessous.
Une mesure traçable est une mesure qui possède une chaîne ininterrompue d’étalonnages remontant jusqu’à l’étalon primaire. Dans le cas des mesures de longueur, l’étalon primaire est la définition du mètre ; la distance parcourue par la lumière dans le vide en 1/299 792 458 secondes, telle que réalisée par le Bureau international des poids et mesures (BIPM) à Paris.
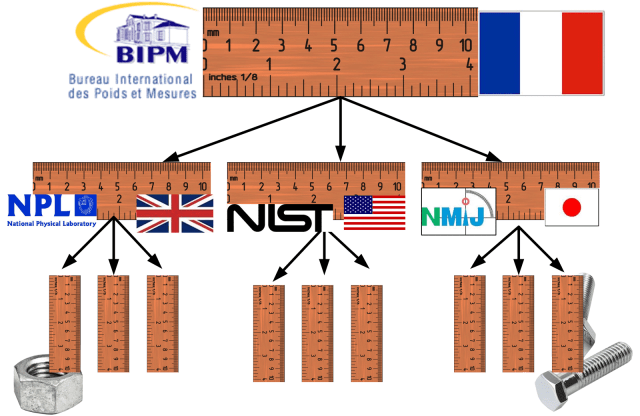
Depuis les années 1930, le pouce est défini comme 25,4 mm et est donc également traçable au même étalon de mètre. Toutes les mesures doivent être traçables jusqu’à la même norme pour garantir que les pièces fabriquées dans différents pays s’emboîtent.
Incertitude et erreur
L’incertitude des mesures provient de différentes sources. Certaines d’entre elles entraîneront une erreur cohérente, ou un biais, dans le résultat.
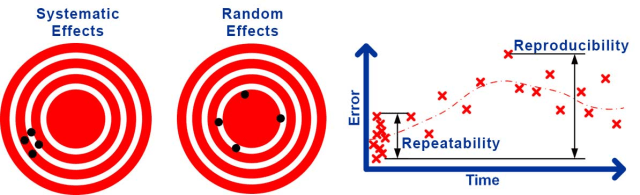
Par exemple, l’erreur inconnue présente lors de l’étalonnage d’un instrument conduira à une erreur constante chaque fois qu’il sera utilisé. Ce type d’effet est connu comme une incertitude systématique conduisant à une erreur systématique . D’autres sources conduiront à des erreurs qui changent aléatoirement à chaque fois qu’une mesure est effectuée.
Par exemple, les turbulences de l’air peuvent provoquer de petites perturbations des mesures laser qui changent de manière aléatoire, les jeux et alignements mécaniques peuvent provoquer une erreur qui change de manière aléatoire dans les mesures mécaniques. Ce type d’effet est connu comme une incertitude aléatoire conduisant à une erreur aléatoire .
Il est classique de diviser l’incertitude aléatoire en répétabilité , l’incertitude aléatoire des résultats dans les mêmes conditions, et reproductibilité , l’incertitude aléatoire dans des conditions modifiées.
Bien sûr, les conditions ne peuvent jamais être exactement les mêmes ou complètement différentes, donc la distinction est quelque peu vague. Les types de conditions qui pourraient être changées sont de faire la mesure à un moment différent, avec un opérateur différent, un instrument différent, en utilisant un étalonnage différent et dans un environnement différent.
Il existe deux méthodes largement utilisées pour quantifier l’incertitude d’une mesure. Les laboratoires d’étalonnage et les institutions scientifiques effectuent normalement l’évaluation de l’incertitude selon le Guide pour l’expression de l’incertitude de mesure (GUM) .
La méthode GUM consiste à considérer d’abord toutes les influences qui peuvent affecter le résultat de la mesure. Il faut ensuite déterminer un modèle mathématique donnant le résultat de la mesure en fonction de ces grandeurs d’influence. En considérant l’incertitude de chaque grandeur d’entrée et en appliquant la ‘ loi de propagation de l’incertitude ‘, une estimation de l’incertitude combinée de la mesure peut être calculée.
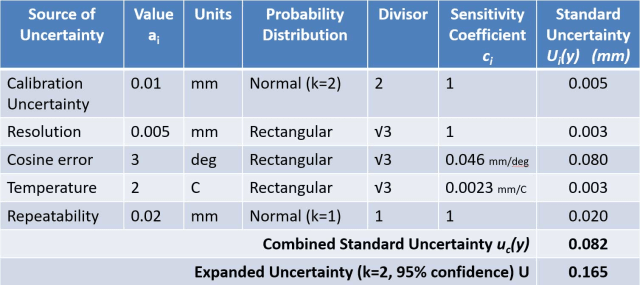
L’approche GUM est parfois décrite comme ascendante , car elle commence par la prise en compte de chaque influence individuelle. Chaque influence est normalement répertoriée dans un tableau appelé budget d’incertitude qui est utilisé pour calculer l’incertitude combinée.
Les processus de mesure industriels sont généralement évalués à l’aide d’une approche d’analyse des systèmes de mesure (MSA), comme le recommande la méthodologie Six-Sigma, et en suivant habituellement les directives du manuel de référence MSA de l’Automotive Industry Action Group (AIAG) .
La MSA consiste à réaliser des études de jaugeage dans lesquelles des mesures répétées sont comparées à une référence dans différentes conditions afin de déterminer le biais, la répétabilité et parfois la reproductibilité.
Une étude de jauge de type 1 est la vérification rapide normalement effectuée pour comprendre initialement la variation d’une jauge. Elle implique qu’un seul opérateur mesure une seule pièce de référence étalonnée 25 fois ou plus et considère ensuite la variation et le biais des résultats. Ce type de test est souvent appelé une étude de répétabilité en dehors de la MSA.
Une étude de répétabilité et de reproductibilité des jauges (Gage R&R) est utilisée pour obtenir une compréhension plus détaillée d’un processus de mesure. Typiquement, 10 pièces sont chacune mesurées deux fois par au moins trois opérateurs différents. Une technique statistique appelée ANOVA est ensuite utilisée pour déterminer la part de variation causée par l’instrument (‘jauge’) et celle causée par l’opérateur. On considère ainsi que le changement d’opérateur et les changements ultérieurs dans le temps et l’environnement constituent une représentation complète des conditions de reproductibilité.
La MSA est parfois qualifiée de descendante car elle traite largement le processus de mesure comme une boîte noire et détermine expérimentalement les incertitudes systématiques et aléatoires. Deux concepts importants dans la MSA sont l’exactitude , utilisée comme l’équivalent de l’incertitude ; et la précision , utilisée comme l’équivalent de l’incertitude aléatoire.
L’avantage de l’évaluation de l’incertitude est qu’elle est capable de considérer toutes les sources d’incertitude et, si elle est faite correctement, elle donne l’estimation la plus précise de l’incertitude. Les problèmes de cette approche comprennent le fait qu’elle nécessite un métrologue capable de produire le modèle mathématique et le risque d’erreur humaine conduisant à l’omission ou à l’estimation incorrecte d’influences importantes.
La méthode GUM n’est également valable que pour une mesure individuelle qui a été effectuée avec des valeurs connues pour toutes les corrections appliquées. Il est donc difficile d’appliquer correctement l’évaluation de l’incertitude pour prédire l’incertitude d’un processus de mesure industriel.
La MSA peut être beaucoup plus facilement appliquée et est destinée à fournir une prédiction pour la précision d’un processus de mesure industriel. Le problème de cette approche est que certains effets systématiques sont ignorés et que les conditions de reproductibilité peuvent ne pas être entièrement représentées, ce qui conduit à une sous-estimation de l’incertitude.
Un exemple de l’omission des effets systématiques est que lors de la détermination du biais, une comparaison est faite avec une référence qui est traitée comme la vraie valeur-en réalité la référence a aussi une incertitude, qui devrait être incluse. Cette méthode repose sur la variation de toutes les conditions de reproductibilité de manière à ce que leurs effets soient visibles dans la variation des résultats lors de mesures répétées. Il est probable que la manière dont ces conditions sont variées ne reflète pas entièrement la variation observée pendant la durée de vie du processus de mesure réel.
Mesures et assurance qualité
Jusqu’à présent, je me suis concentré sur le contrôle de la qualité, c’est-à-dire sur la façon dont les mesures peuvent prouver que les pièces sont conformes aux spécifications après avoir été produites. Maintenant, considérons brièvement l’assurance qualité, c’est-à-dire la façon dont nous nous assurons que le processus produit de bonnes pièces en premier lieu.
Cet aspect de la qualité est largement abordé par le contrôle statistique des processus (SPC) . On peut évaluer un processus en fabriquant plusieurs pièces et en les mesurant pour déterminer la variation et le biais du processus de fabrication. Plutôt que de donner ces résultats directement, il est normal de diviser la tolérance de la pièce par la précision du processus pour donner la capacité de la machine-outil ( C P ) ou par la précision du processus pour donner la capacité du processus ( C PK ).
La SPC est à bien des égards équivalente à la MSA. Elle adopte une approche descendante pour comprendre les effets aléatoires et systématiques. Cependant, au lieu d’évaluer les mesures, elle est utilisée pour évaluer les sorties du processus. Il a généralement les mêmes avantages et inconvénients que MSA, et une approche ascendante d’évaluation de l’incertitude peut être utilisée si ceux-ci sont une préoccupation.
Il peut sembler initialement qu’il existe des différences fondamentales entre MSA et SPC en raison de la terminologie très différente au sein de SPC. Cependant, la variation de cause commune (ou variation de cause fortuite dans la littérature plus ancienne) est l’équivalent de la précision ; la variabilité à court terme est l’équivalent de la répétabilité ; la variabilité à long terme est l’équivalent de la reproductibilité ; et la variation de cause spéciale (ou variation de cause assignable dans la littérature plus ancienne) est l’équivalent du biais.
La MSP met également beaucoup plus l’accent sur la garantie qu’un processus est en ‘ contrôle statistique ‘. En termes généraux, cela signifie que les effets sont aléatoires et normalement distribués et que tout effet systématique significatif est corrigé. C’est un point fort du SPC et il est parfois négligé à la fois dans l’évaluation de l’incertitude et dans l’ASM.
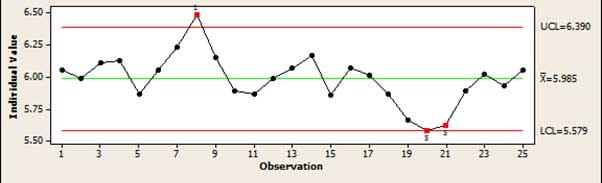
Le principal outil utilisé en SPC pour vérifier un processus ‘en contrôle’ est la carte de contrôle . Cela donne une vue graphique simple d’un processus qui permet de repérer facilement quand un processus dérive ou produit des erreurs qui ne peuvent pas être expliquées par des variations aléatoires normales. Par exemple, si plusieurs points sont tous en augmentation ou en diminution, cela indique que le processus dérive.
Dans cet article, j’ai essayé de donner un large aperçu d’un sujet vaste et complexe. J’ai présenté les principes fondamentaux du maintien de la qualité sans entrer dans les mathématiques nécessaires à l’application de ces méthodes.
Restez à l’écoute pour de futurs articles sur ces sujets.

La carrière d’ingénieur du Dr Jody Muelaner, qui a duré 20 ans, a commencé dans la conception de machines, travaillant sur tout, des appareils médicaux aux scieries. Depuis 2007, il développe une nouvelle métrologie à l’université de Bath, en étroite collaboration avec des entreprises aérospatiales de premier plan. Cette recherche se concentre actuellement sur la modélisation de l’incertitude des systèmes de production, en réunissant des éléments de SPC, MSA et de métrologie avec de nouvelles méthodes numériques. Il s’intéresse également à la conception de vélos. Visitez son site web pour plus d’informations.