Dans le tutoriel sur les modèles linéaires généralisés, nous avons appris les différents GLM comme la régression linéaire, la régression logistique, etc. Dans ce tutoriel de la série de tutoriels R de TechVidvan, nous allons examiner en détail la régression linéaire en R. Nous apprendrons ce qu’est la régression linéaire en R et comment l’implémenter en R. Nous examinerons la méthode d’estimation des moindres carrés et nous apprendrons également comment vérifier la précision du modèle.

Donc, sans plus attendre, commençons !

Régression linéaire en R

La régression linéaire en R est une méthode utilisée pour prédire la valeur d’une variable en utilisant la ou les valeurs d’une ou plusieurs variables prédicteurs d’entrée. Le but de la régression linéaire est d’établir une relation linéaire entre la variable de sortie souhaitée et les prédicteurs d’entrée.

Modéliser une variable continue Y comme une fonction d’une ou plusieurs variables prédicteurs d’entrée Xi, de sorte que la fonction puisse être utilisée pour prédire la valeur de Y lorsque seules les valeurs de Xi sont connues. La forme générale d’une telle relation linéaire est :

Y=?0+?1 X

Ici, ?0 est l’intercept
et ?1 est la pente.

Types de régression linéaire dans R

Il existe deux types de régression linéaire dans R :

• Régression linéaire simple
• Régression linéaire multiple

Regardons-les un par un.

Régression linéaire simple dans R

La régression linéaire simple vise à trouver une relation linéaire entre deux variables continues. Il est important de noter que cette relation est de nature statistique et non déterministe.

Une relation déterministe est une relation où la valeur d’une variable peut être trouvée avec précision en utilisant la valeur de l’autre variable. Un exemple de relation déterministe est celle qui existe entre les kilomètres et les miles. En utilisant la valeur du kilomètre, nous pouvons trouver avec précision la distance en miles. Une relation statistique n’est pas précise et comporte toujours une erreur de prédiction. Par exemple, avec suffisamment de données, nous pouvons trouver une relation entre la taille et le poids d’une personne, mais il y aura toujours une marge d’erreur et des cas exceptionnels existeront.

L’idée derrière la régression linéaire simple est de trouver une ligne qui correspond le mieux aux valeurs données des deux variables. Cette ligne peut alors nous aider à trouver les valeurs de la variable dépendante lorsqu’elles sont manquantes.

Etudions cela à l’aide d’un exemple. Nous disposons d’un jeu de données constitué des tailles et des poids de 500 personnes. Notre objectif ici est de construire un modèle de régression linéaire qui formule la relation entre la taille et le poids, de telle sorte que lorsque nous donnons la taille (Y) en entrée du modèle, il puisse nous donner le poids (X) en retour avec une marge ou une erreur minimale.

Y=b0+b1X

Les valeurs de b0 et b1 doivent être choisies de manière à minimiser la marge d’erreur. La métrique d’erreur peut être utilisée pour mesurer la précision du modèle.

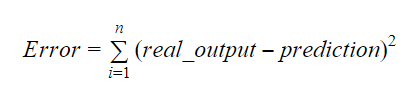
Nous pouvons calculer la pente ou le coefficient comme: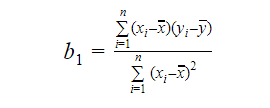

La valeur de b1 nous donne un aperçu de la nature de la relation entre les variables dépendantes et indépendantes.

• Si b1 > 0, alors les variables ont une relation positive c’est-à-dire. une augmentation de x entraînera une augmentation de y.
• Si b1 < 0, alors les variables ont une relation négative c’est-à-dire qu’une augmentation de x entraînera une diminution de y.

La valeur de b0 ou intercept peut être calculée comme suit :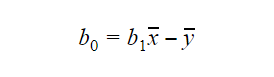
La valeur de b0 peut également donner beaucoup d’informations sur le modèle et vice-versa.

Si le modèle n’inclut pas x=0, alors la prédiction n’a aucun sens sans b1. Pour que le modèle ne comporte que b0 et pas b1 à un moment donné, il faut que la valeur de x soit 0 à ce moment-là. Dans des cas tels que la hauteur, x ne peut pas être 0 et la hauteur d’une personne ne peut pas être 0. Par conséquent, un tel modèle n’a aucun sens avec seulement b0.

Si le terme b0 est manquant, alors le modèle passera par l’origine, ce qui signifie que la prédiction et le coefficient de régression(pente) seront biaisés.

Régression linéaire multiple dans R

La régression linéaire multiple est une extension de la régression linéaire simple. Dans la régression linéaire multiple, nous cherchons à créer un modèle linéaire capable de prédire la valeur de la variable cible à l’aide des valeurs de plusieurs variables prédictives. La forme générale d’une telle fonction est la suivante :

Y=b0+b1X1+b2X2+…+bnXn

Évaluer la précision du modèle

Il existe différentes méthodes pour évaluer la qualité et la précision du modèle. Examinons certaines de ces méthodes une par une.

R-carré

La véritable information contenue dans les données est la variance qu’elles véhiculent. Le R-carré nous indique la proportion de la variation de la variable cible (y) expliquée par le modèle. Nous pouvons trouver la mesure du R-carré d’un modèle en utilisant la formule suivante :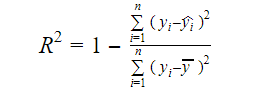

Où,

• yi est la valeur ajustée de y pour l’observation i
• y est la moyenne de Y.

Une valeur plus faible du R-carré signifie une précision plus faible du modèle. Cependant, la mesure du R-carré n’est pas nécessairement un facteur décisif final.

R-carré ajusté

Lorsque le nombre de variables augmente dans le modèle, la valeur du R-carré augmente également. Cela entraîne également des erreurs dans la variation expliquée par les variables nouvellement ajoutées. Par conséquent, nous ajustons la formule du R carré pour les variables multiples.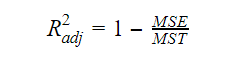
Ici, le MSE représente l’erreur standard moyenne qui est :

Et le MST représente le total standard moyen qui est donné par :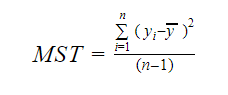

Où, n est le nombre d’observations et q est le nombre de coefficients.

La relation entre le R-carré et le R-carré ajusté est: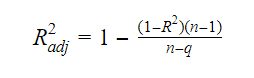

Erreur standard et F-statistique

L’erreur standard et la F-statistique sont toutes deux des mesures de la qualité de l’ajustement d’un modèle. Les formules de l’erreur standard et de la statistique F sont :

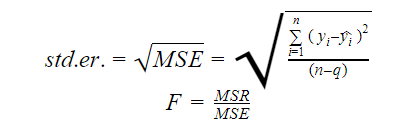
Où MSR signifie Mean Square Regression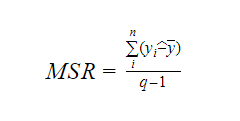

AIC et BIC

Le critère d’information d’Akaike et le critère d’information bayésien sont des mesures de la qualité de l’ajustement des modèles statistiques. Ils peuvent également être utilisés comme critères de sélection d’un modèle.

AIC=(-2)*ln(L)+2*k
BIC=(-2)*ln(L)+k*ln(n)

Où,

• L est la fonction de vraisemblance,
• k est le nombre de paramètres du modèle,
• n est la taille de l’échantillon.

Fonction lm dans R

La fonction lm() de R ajuste des modèles linéaires. Elle peut effectuer des régressions et des analyses de variance et de covariance. La syntaxe de la fonction lm est la suivante :

lm(formula, data, subset, weights, na.action,method = "qr", model = TRUE, x = FALSE, y = FALSE, qr = TRUE,singular.ok = TRUE, offset, …)

Où,

• formule est un objet de la classe « formula » et est une représentation symbolique du modèle à ajuster,
• données est le cadre de données ou la liste qui contient les variables de la formule(data est un argument facultatif. S’il est manquant, la fonction prend les variables de l’environnement),
• subset est un vecteur optionnel contenant un sous-ensemble d’observations qui doivent être utilisées dans le processus d’ajustement,
• weights est un vecteur optionnel qui spécifie les poids à utiliser dans le processus d’ajustement,
• na.action est une fonction qui montre ce qui doit se passer lorsque des NA sont rencontrés dans les données,
• method signifie la méthode d’ajustement du modèle,
• model, x, y, et qr sont des logiques qui contrôlent si les valeurs correspondantes doivent être retournées avec la sortie ou non. Ces valeurs sont :
• modèle : le cadre du modèle
• x : la matrice du modèle
• y : la réponse
• qr : la décomposition qr
• singulier.ok est une logique qui contrôle si les ajustements singuliers sont autorisés ou non,
• offset est un prédicteur connu à l’avance qui doit être utilisé dans le modèle,
• . . sont des arguments supplémentaires à passer aux fonctions de régression de niveau inférieur.

Exemple pratique de régression linéaire dans R

C’est assez de théorie pour le moment. Voyons comment mettre tout cela en œuvre. Nous allons ajuster un modèle linéaire en utilisant la régression linéaire dans R avec l’aide de la fonction lm(). Nous allons également vérifier la qualité de l’ajustement du modèle par la suite. Utilisons le jeu de données des voitures qui est fourni par défaut dans le package R de base.

1. Commençons par une analyse graphique du jeu de données pour nous familiariser avec lui. Pour ce faire, nous allons dessiner un diagramme de dispersion et vérifier ce qu’il nous dit sur les données.

Nous pouvons utiliser la fonction scatter.smooth() pour créer un diagramme de dispersion pour l’ensemble de données.

scatter.smooth(x=cars$speed,y=cars$dist,main="TechVidvan Dist ~ Speed")

Sortie

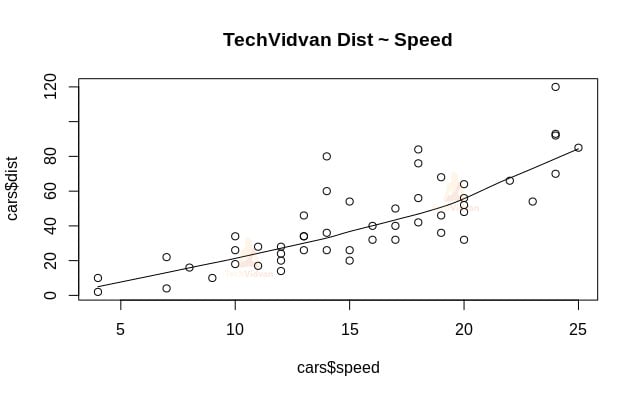
Le diagramme de dispersion nous montre une corrélation positive entre la distance et la vitesse. Il suggère une relation linéairement croissante entre les deux variables. Cela rend les données appropriées pour la régression linéaire car une relation linéaire est une hypothèse de base pour l’ajustement d’un modèle linéaire sur les données.

2. Maintenant que nous avons vérifié que la régression linéaire est appropriée pour les données, nous pouvons utiliser la fonction lm() pour y ajuster un modèle linéaire.

Linear_model <- lm(dist~speed,data=cars)print(Linear_model)

Sortie

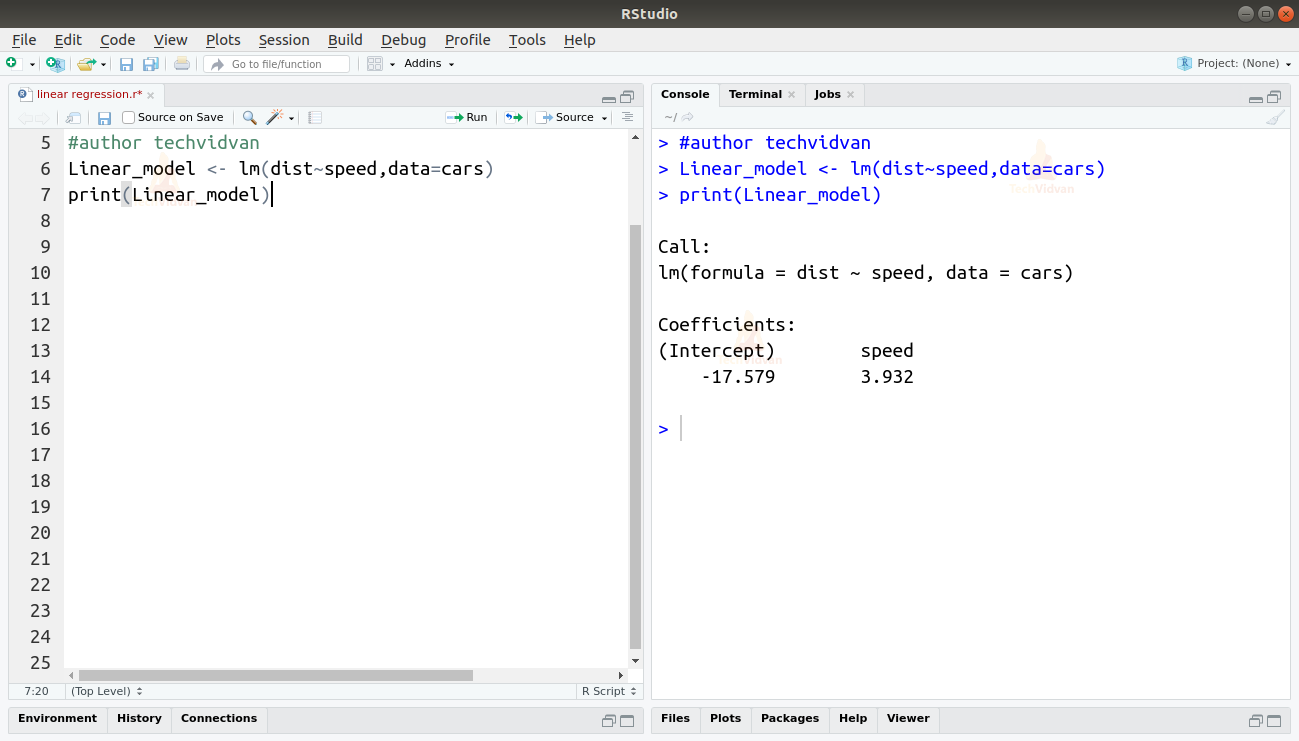
La sortie de la fonction lm() nous montre l’intercept et le coefficient de vitesse. Ainsi, définissant la relation linéaire entre la distance et la vitesse comme:

Distance=Intercept+coefficient*vitesse

Distance=-17.579+3.932*vitesse

3. Maintenant que nous avons ajusté un modèle, vérifions la qualité ou la justesse de l’ajustement. Commençons par vérifier le résumé du modèle linéaire en utilisant la fonction summary().

summary(Linear_model)

Sortie

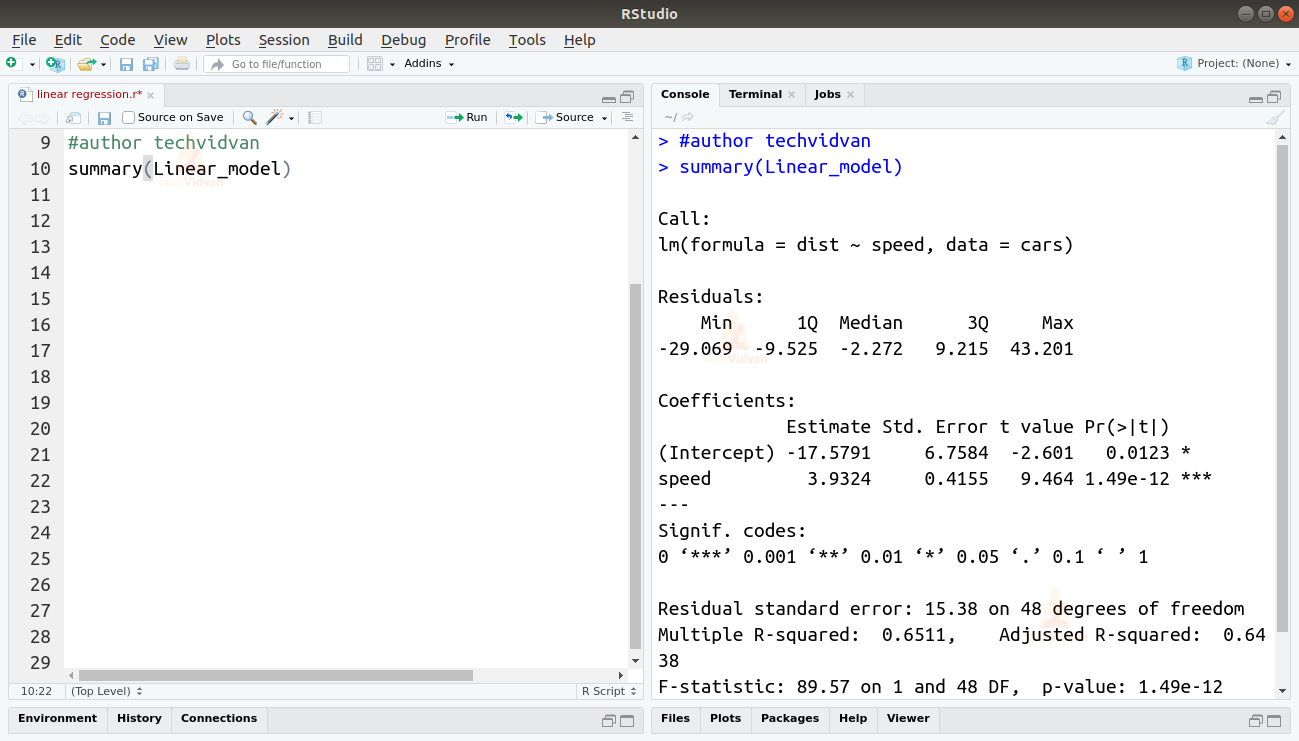
La fonction summary() nous donne quelques mesures importantes pour aider à diagnostiquer l’ajustement du modèle. La valeur p est une mesure importante de la qualité de l’ajustement d’un modèle. On dit qu’un modèle n’est pas ajusté si la valeur p est supérieure à un niveau de signification statistique prédéterminé qui est idéalement de 0,05.

Le résumé nous fournit également la valeur t. Plus la valeur t est élevée, plus le modèle est bien ajusté.
Nous pouvons également trouver l’AIC et le BIC en utilisant les fonctions AIC() et BIC().

AIC(Linear_model)BIC(Linear_model)

Sortie

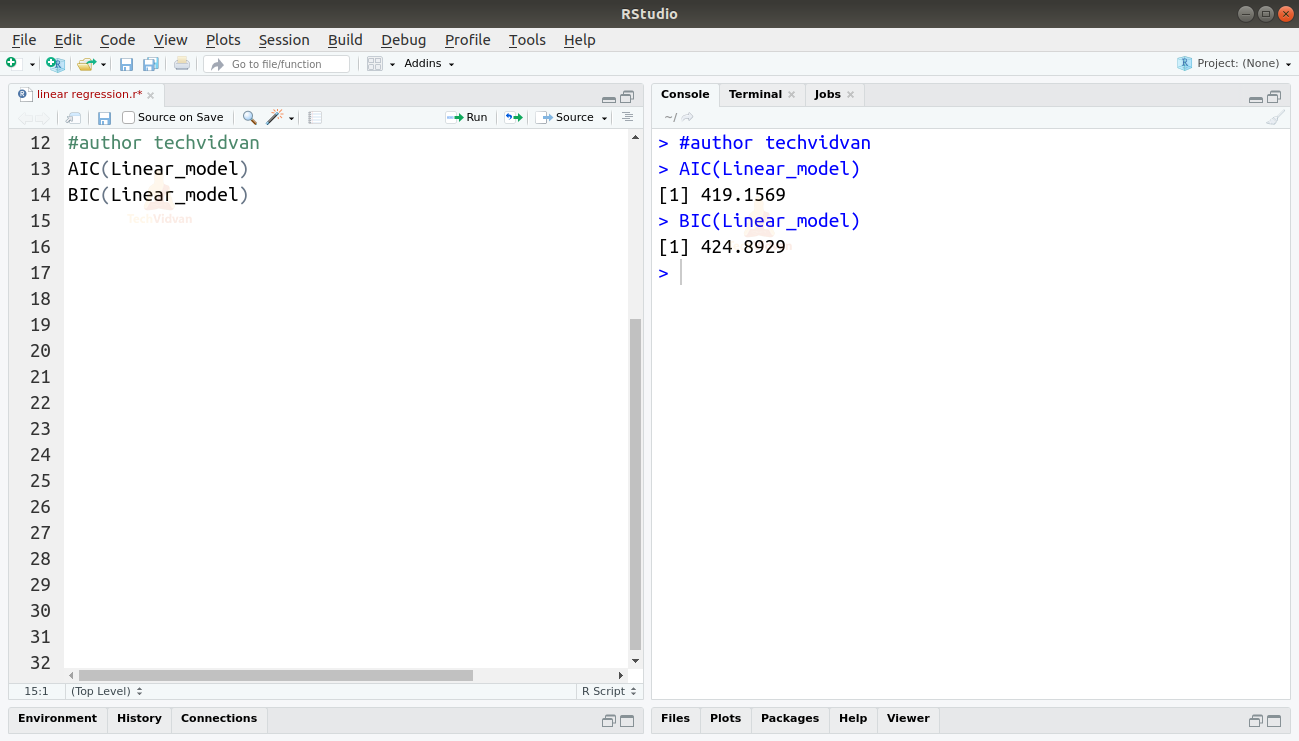
Le modèle qui entraîne les scores AIC et BIC les plus bas est le plus préféré.

Sommaire

Dans ce chapitre de la série de tutoriels R de TechVidvan, nous avons appris la régression linéaire. Nous avons appris la régression linéaire simple et la régression linéaire multiple. Puis nous avons étudié différentes mesures pour évaluer la qualité ou la précision du modèle, comme le R2, le R2 ajusté, l’erreur standard, les statistiques F, l’AIC et le BIC. Nous avons ensuite appris à mettre en œuvre la régression linéaire dans R. Nous avons ensuite vérifié la qualité de l’ajustement du modèle dans R.

Partagez votre évaluation sur Google si vous avez aimé le tutoriel sur la régression linéaire.