Un métamatériau électromagnétique affecte les ondes électromagnétiques qui frappent ou interagissent avec ses caractéristiques structurelles, qui sont plus petites que la longueur d’onde. Pour se comporter comme un matériau homogène décrit avec précision par un indice de réfraction effectif, ses caractéristiques doivent être beaucoup plus petites que la longueur d’onde.
Pour le rayonnement micro-ondes, les caractéristiques sont de l’ordre du millimètre. Les métamatériaux à fréquence micro-ondes sont généralement construits comme des réseaux d’éléments électriquement conducteurs (tels que des boucles de fil) qui ont des caractéristiques inductives et capacitives appropriées. De nombreux métamatériaux micro-ondes utilisent des résonateurs à anneau fendu.
Les métamatériaux photoniques sont structurés à l’échelle nanométrique et manipulent la lumière à des fréquences optiques. Les cristaux photoniques et les surfaces sélectives en fréquence telles que les réseaux de diffraction, les miroirs diélectriques et les revêtements optiques présentent des similitudes avec les métamatériaux structurés à l’échelle sub-longueur d’onde. Cependant, ces derniers sont généralement considérés comme distincts des métamatériaux, car leur fonction découle de la diffraction ou de l’interférence et ne peut donc pas être assimilée à un matériau homogène. Cependant, les structures matérielles telles que les cristaux photoniques sont efficaces dans le spectre de la lumière visible. Le milieu du spectre visible a une longueur d’onde d’environ 560 nm (pour la lumière du soleil). Les structures de cristaux photoniques ont généralement la moitié de cette taille ou moins, c’est-à-dire <280 nm.
Les métamatériaux plasmoniques utilisent des plasmons de surface, qui sont des paquets de charge électrique qui oscillent collectivement à la surface des métaux à des fréquences optiques.
Les surfaces sélectives en fréquence (SFS) peuvent présenter des caractéristiques sub-longueur d’onde et sont connues sous le nom de conducteurs magnétiques artificiels (AMC) ou de surfaces à haute impédance (HIS). Les FSS présentent des caractéristiques inductives et capacitives qui sont directement liées à leur structure sub-longueur d’onde.
Les métamatériaux électromagnétiques peuvent être divisés en différentes classes, comme suit :
Indice de réfraction négatifEdit
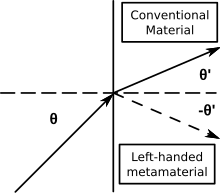
Les métamatériaux à indice négatif (MNI) sont caractérisés par un indice de réfraction négatif. D’autres termes pour désigner les MNI comprennent les « milieux gauchers », les « milieux à indice de réfraction négatif » et les « milieux à onde arrière ». Les MNI où l’indice de réfraction négatif provient simultanément d’une permittivité négative et d’une perméabilité négative sont également connus sous le nom de métamatériaux doublement négatifs ou de matériaux doublement négatifs (DNG).
En supposant un matériau bien approché par une permittivité et une perméabilité réelles, la relation entre la permittivité ϵ r {\displaystyle \epsilon _{r}}.

, perméabilité μ r {\displaystyle \mu _{r}}

et l’indice de réfraction n est donné par n = ± ϵ r μ r {\displaystyle \scriptstyle n=\pm {\sqrt {\epsilon _{\mathrm {r} }\mu _{\mathrm {r} }}}}

. Tous les matériaux transparents non métamatériaux connus (verre, eau, …) possèdent un ϵ r positif {\displaystyle \epsilon _{r}}.

et μ r {\displaystyle \mu _{r}}

. Par convention, la racine carrée positive est utilisée pour n. Cependant, certains métamatériaux techniques ont ϵ r {\displaystyle \epsilon _{r}}

et μ r < 0 {\displaystyle \mu _{r}<0}

. Parce que le produit ϵ r μ r {\displaystyle \epsilon _{r}\mu _{r}}

est positif, n est réel. Dans ces circonstances, il est nécessaire de prendre la racine carrée négative de n. Lorsque les deux ϵ r {\displaystyle \epsilon _{r}}

et μ r {\displaystyle \mu _{r}}

sont positifs (négatifs), les ondes se propagent dans le sens avant (arrière). Les ondes électromagnétiques ne peuvent pas se propager dans les matériaux avec ϵ r {\displaystyle \epsilon _{r}}

et μ r {\displaystyle \mu _{r}}

de signe opposé lorsque l’indice de réfraction devient imaginaire. De tels matériaux sont opaques au rayonnement électromagnétique et on peut citer à titre d’exemple les matériaux plasmoniques tels que les métaux (or, argent, …).
Les considérations précédentes sont simplistes pour les matériaux réels, qui doivent avoir une valeur complexe ϵ r {\displaystyle \epsilon _{r}}.

et μ r {\displaystyle \mu _{r}}

. Les parties réelles des deux ϵ r {\displaystyle \epsilon _{r}}

et μ r {\displaystyle \mu _{r}}

n’ont pas besoin d’être négatifs pour qu’un matériau passif présente une réfraction négative. En effet, un indice de réfraction négatif pour des ondes polarisées circulairement peut également provenir de la chiralité. Les métamatériaux à n négatif présentent de nombreuses propriétés intéressantes :
- La loi de Snell (n1sinθ1 = n2sinθ2) décrit toujours la réfraction, mais comme n2 est négatif, les rayons incidents et réfractés sont du même côté de la normale à la surface à une interface de matériaux à indice positif et négatif.
- Le rayonnement Cherenkov pointe dans l’autre sens.
- Le vecteur de Poynting moyenné dans le temps est antiparallèle à la vitesse de phase. Cependant, pour que les ondes (énergie) se propagent, un -µ doit être apparié à un -ε afin de satisfaire la dépendance du nombre d’onde aux paramètres matériels k c = ω μ ϵ {\displaystyle kc=\omega {\sqrt {\mu \epsilon }}.
.
L’indice de réfraction négatif dérive mathématiquement du triplet de vecteurs E, H et k.
Pour les ondes planes se propageant dans les métamatériaux électromagnétiques, le champ électrique, le champ magnétique et le vecteur d’onde suivent une règle de gauche, l’inverse du comportement des matériaux optiques conventionnels.
À ce jour, seuls les métamatériaux présentent un indice de réfraction négatif.
Négatif simpleEdit
Les métamatériaux négatifs simples (SNG) ont soit une permittivité relative négative (εr), soit une perméabilité relative négative (µr), mais pas les deux. Ils agissent comme des métamatériaux lorsqu’ils sont combinés avec un SNG différent et complémentaire, agissant conjointement comme un DNG.
Les milieux négatifs epsilon (ENG) présentent un εr négatif alors que µr est positif. De nombreux plasmas présentent cette caractéristique. Par exemple, les métaux nobles comme l’or ou l’argent sont des ENG dans les spectres infrarouge et visible.
Les milieux négatifs Mu (MNG) affichent un εr positif et un µr négatif. Les matériaux gyrotropes ou gyromagnétiques présentent cette caractéristique. Un matériau gyrotrope est un matériau altéré par la présence d’un champ magnétique quasi-statique, permettant un effet magnéto-optique. L’effet magnéto-optique est un phénomène dans lequel une onde électromagnétique se propage dans un tel milieu. Dans un tel matériau, les polarisations elliptiques de rotation gauche et droite peuvent se propager à des vitesses différentes. Lorsque la lumière est transmise à travers une couche de matériau magnéto-optique, le résultat est appelé effet Faraday : le plan de polarisation peut être tourné, formant un rotateur de Faraday. Les résultats d’une telle réflexion sont connus sous le nom d’effet Kerr magnéto-optique (à ne pas confondre avec l’effet Kerr non linéaire). Deux matériaux gyrotropes dont les sens de rotation des deux polarisations principales sont inversés sont appelés isomères optiques.
La jonction d’une dalle de matériau ENG et d’une dalle de matériau MNG a permis d’obtenir des propriétés telles que des résonances, un effet tunnel anormal, une transparence et une réflexion nulle. Comme les matériaux d’indice négatif, les SNG sont intrinsèquement dispersifs, ainsi leurs εr, µr et indice de réfraction n, sont fonction de la fréquence.
Métamatériaux hyperboliquesEdit
Les métamatériaux hyperboliques (HMM) se comportent comme un métal pour une certaine polarisation ou direction de propagation de la lumière et se comportent comme un diélectrique pour l’autre en raison des composantes négatives et positives du tenseur de permittivité, ce qui donne une anisotropie extrême. La relation de dispersion du matériau dans l’espace du vecteur d’onde forme un hyperboloïde et on l’appelle donc un métamatériau hyperbolique. L’anisotropie extrême des HMMs conduit à une propagation directionnelle de la lumière à l’intérieur et sur la surface. Les HMMs ont montré diverses applications potentielles, telles que la détection, l’imagerie, la direction des signaux optiques, les effets de résonance plasmonique améliorés.
Bande interditeEdit
Les métamatériaux à bande interdite électromagnétique (EBG ou EBM) contrôlent la propagation de la lumière. Ceci est accompli soit avec des cristaux photoniques (PC), soit avec des matériaux gauchers (LHM). Les PC peuvent interdire complètement la propagation de la lumière. Les deux catégories peuvent permettre à la lumière de se propager dans des directions spécifiques et conçues, et les deux peuvent être conçues avec des bandes interdites aux fréquences souhaitées. La taille de la période des EBG est une fraction appréciable de la longueur d’onde, créant des interférences constructives et destructives.
Les PC se distinguent des structures sous-longueur d’onde, telles que les métamatériaux accordables, car le PC tire ses propriétés de ses caractéristiques de bande interdite. Les PC sont dimensionnés pour correspondre à la longueur d’onde de la lumière, contrairement à d’autres métamatériaux qui exposent une structure sub-longueur d’onde. En outre, les PC fonctionnent en diffractant la lumière. En revanche, le métamatériau n’utilise pas la diffraction.
Les PCs ont des inclusions périodiques qui inhibent la propagation des ondes en raison de l’interférence destructive des inclusions due à la diffusion. La propriété de bande interdite photonique des PC en fait l’analogue électromagnétique des cristaux semi-conducteurs électroniques.
Les EBG ont pour objectif de créer des structures diélectriques périodiques de haute qualité, à faibles pertes. Un EBG affecte les photons de la même manière que les matériaux semi-conducteurs affectent les électrons. Les PC sont le matériau à bande interdite parfait, car ils ne permettent aucune propagation de la lumière. Chaque unité de la structure périodique prescrite agit comme un atome, bien que de taille beaucoup plus grande.
Les EBG sont conçus pour empêcher la propagation d’une bande passante de fréquences allouée, pour certains angles d’arrivée et certaines polarisations. Diverses géométries et structures ont été proposées pour fabriquer les propriétés spéciales des EBG. En pratique, il est impossible de construire un dispositif EBG sans défaut.
Les EBG ont été fabriqués pour des fréquences allant de quelques gigahertz (GHz) à quelques térahertz (THz), dans les régions de fréquences radio, micro-ondes et infrarouge moyen. Les développements d’applications EBG comprennent une ligne de transmission, des pieux de bois constitués de barres diélectriques carrées et plusieurs types différents d’antennes à faible gain.
Milieu doublement positifEdit
Les milieux doublement positifs (MDP) existent dans la nature, comme les diélectriques naturels. La permittivité et la perméabilité magnétique sont toutes deux positives et la propagation des ondes se fait dans le sens direct. Des matériaux artificiels ont été fabriqués qui combinent les propriétés DPS, ENG et MNG.
Bi-isotrope et bianisotropeEdit
La catégorisation des métamatériaux en double ou simple négatif, ou double positif, suppose normalement que le métamatériau a des réponses électriques et magnétiques indépendantes décrites par ε et µ. Cependant, dans de nombreux cas, le champ électrique provoque une polarisation magnétique, tandis que le champ magnétique induit une polarisation électrique, connue sous le nom de couplage magnétoélectrique. De tels milieux sont qualifiés de bi-isotropes. Les milieux qui présentent un couplage magnétoélectrique et qui sont anisotropes (ce qui est le cas de nombreuses structures métamatérielles), sont qualifiés de bi-anisotropes.
Quatre paramètres matériels sont intrinsèques au couplage magnétoélectrique des milieux bi-isotropes. Il s’agit des intensités de champ électrique (E) et magnétique (H), et des densités de flux électrique (D) et magnétique (B). Ces paramètres sont ε, µ, κ et χ ou respectivement la permittivité, la perméabilité, la force de chiralité et le paramètre de Tellegen. Dans ce type de milieux, les paramètres matériels ne varient pas avec les changements le long d’un système de coordonnées de mesures tourné. En ce sens, ils sont invariants ou scalaires.
Les paramètres magnétoélectriques intrinsèques, κ et χ, affectent la phase de l’onde. L’effet du paramètre de chiralité est de diviser l’indice de réfraction. Dans les milieux isotropes, cela entraîne la propagation de l’onde uniquement si ε et µ ont le même signe. Dans les milieux bi-isotropes où χ est supposé être nul et κ une valeur non nulle, des résultats différents apparaissent. Soit une onde arrière, soit une onde avant peut se produire. Alternativement, deux ondes avant ou deux ondes arrière peuvent se produire, selon la force du paramètre de chiralité.
Dans le cas général, les relations constitutives pour les matériaux bi-anisotropes se lisent D = ϵ E + ξ H , {\displaystyle \mathbf {D} =\epsilon \mathbf {E} +\xi \mathbf {H} ,}

B = ζ E + μ H , {\displaystyle \mathbf {B} =\zeta \mathbf {E} +\mu \mathbf {H} ,}

où ϵ {\displaystyle \epsilon }

et μ {\displaystyle \mu }

sont les tenseurs de permittivité et de perméabilité, respectivement, tandis que ξ {\displaystyle \xi }

et ζ {\displaystyle \zeta }

sont les deux tenseurs magnéto-électriques. Si le milieu est réciproque, permittivité et perméabilité sont des tenseurs symétriques, et ξ = – ζ T = – i κ T {\displaystyle \xi =-\zeta ^{T}=-i\kappa ^{T}}

, où κ {\displaystyle \kappa }

est le tenseur chiral décrivant la réponse chirale électromagnétique et magnéto-électrique réciproque. Le tenseur chiral peut être exprimé par κ = 1 3 tr ( κ ) I + N + J {\displaystyle \kappa ={\tfrac {1}{3}}\operatorname {tr} (\kappa )I+N+J}

, où tr ( κ ) {\displaystyle \operatorname {tr} (\kappa )}

est la trace de κ {\displaystyle \kappa }

, I est la matrice identité, N est un tenseur symétrique sans trace, et J est un tenseur antisymétrique. Une telle décomposition nous permet de classer la réponse bianisotrope réciproque et nous pouvons identifier les trois classes principales suivantes : (i) milieu chiral ( tr ( κ ) ≠ 0 , N ≠ 0 , J = 0 {\displaystyle \operatorname {tr} (\kappa )\neq 0,N\neq 0,J=0}

), (ii) les milieux pseudochiraux ( tr ( κ ) = 0 , N ≠ 0 , J = 0 {\displaystyle \operatorname {tr}) (\kappa )=0,N\neq 0,J=0}

), (iii) milieu oméga ( tr ( κ ) = 0 , N = 0 , J ≠ 0 {\displaystyle \operatorname {tr} (\kappa )=0,N=0,J\neq 0}

).
ChiralEdit
La maniabilité des métamatériaux est une source potentielle de confusion car la littérature sur les métamatériaux comprend deux utilisations contradictoires des termes gaucher et droitier. Le premier fait référence à l’une des deux ondes polarisées circulairement qui sont les modes de propagation dans les milieux chiraux. Le second se rapporte au triplet de champ électrique, de champ magnétique et de vecteur de Poynting qui apparaît dans les milieux à indice de réfraction négatif, qui dans la plupart des cas ne sont pas chiraux.
Généralement, une réponse électromagnétique chirale et/ou bianisotrope est une conséquence de la chiralité géométrique 3D : les métamatériaux 3D-chiraux sont composés par l’intégration de structures 3D-chirales dans un milieu hôte et ils présentent des effets de polarisation liés à la chiralité tels que l’activité optique et le dichroïsme circulaire. Le concept de chiralité 2D existe également et un objet plan est dit chiral s’il ne peut être superposé à son image miroir à moins d’être soulevé du plan. On a observé que les métamatériaux 2D-chiraux anisotropes et à pertes présentent une transmission (réflexion, absorption) directionnellement asymétrique d’ondes polarisées circulairement en raison du dichroïsme de conversion circulaire. D’autre part, une réponse bianisotrope peut provenir de structures géométriques achirales ne possédant pas de chiralité intrinsèque 2D ou 3D. Plum et ses collègues ont étudié le couplage magnéto-électrique dû à la chiralité extrinsèque, où la disposition d’une structure (achirale) avec le vecteur d’onde de rayonnement est différente de son image miroir, et ont observé une activité optique linéaire, une activité optique non linéaire, une activité optique spéculaire et un dichroïsme de conversion circulaire importants et accordables. Rizza et al. ont suggéré des métamatériaux chiraux 1D où le tenseur de chiralité effective n’est pas évanouissant si le système est géométriquement chiral unidimensionnel (l’image miroir de la structure entière ne peut pas lui être superposée en utilisant des translations sans rotations).
Les métamatériaux chiraux 3D sont construits à partir de matériaux ou de résonateurs chiraux dans lesquels le paramètre de chiralité effective κ {\displaystyle \kappa }.

est non nul. Les propriétés de propagation des ondes dans de tels métamatériaux chiraux démontrent que la réfraction négative peut être réalisée dans des métamatériaux avec une forte chiralité et un ϵ r positif {\displaystyle \epsilon _{r}}.

et μ r {\displaystyle \mu _{r}}

. Ceci est dû au fait que l’indice de réfraction n {\displaystyle n}

a des valeurs distinctes pour les ondes polarisées circulairement à gauche et à droite, données par
n = ± ϵ r μ r ± κ {\displaystyle n=\pm {\sqrt {\epsilon _{r}\mu _{r}}\pm \kappa }.

On peut voir qu’un indice négatif se produira pour une polarisation si κ {\displaystyle \kappa }

> ϵ r μ r {\displaystyle {\sqrt {\epsilon _{r}\mu _{r}}}}}.

. Dans ce cas, il n’est pas nécessaire que l’un ou l’autre ou les deux ϵ r {\displaystyle \epsilon _{r}}

et μ r {\displaystyle \mu _{r}}

être négatifs pour la propagation des ondes vers l’arrière. Un indice de réfraction négatif dû à la chiralité a été observé pour la première fois simultanément et indépendamment par Plum et al. et Zhang et al. en 2009.
FSS basedEdit
Les métamatériaux à base de surfaces sélectives en fréquence bloquent les signaux dans une bande d’onde et laissent passer ceux d’une autre bande d’onde. Ils sont devenus une alternative aux métamatériaux à fréquence fixe. Ils permettent des changements optionnels de fréquences dans un seul milieu, plutôt que les limitations restrictives d’une réponse en fréquence fixe.
