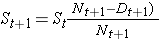Nous sommes souvent intéressés à évaluer s’il existe des différences de survie (ou d’incidence cumulative d’événement) entre différents groupes de participants. Par exemple, dans un essai clinique avec un résultat de survie, nous pourrions être intéressés à comparer la survie entre les participants recevant un nouveau médicament par rapport à un placebo (ou un traitement standard). Dans une étude d’observation, on peut vouloir comparer la survie entre les hommes et les femmes, ou entre les participants avec et sans un facteur de risque particulier (par exemple, l’hypertension ou le diabète). Il existe plusieurs tests pour comparer la survie entre des groupes indépendants.

Le test du log rank

Le test du log rank est un test populaire pour tester l’hypothèse nulle d’absence de différence de survie entre deux ou plusieurs groupes indépendants. Le test compare l’ensemble de l’expérience de survie entre les groupes et peut être considéré comme un test permettant de déterminer si les courbes de survie sont identiques (se chevauchent) ou non. Les courbes de survie sont estimées pour chaque groupe, considéré séparément, à l’aide de la méthode Kaplan-Meier et comparées statistiquement à l’aide du test du log rank. Il est important de noter qu’il existe plusieurs variantes de la statistique du test du log rank qui sont mises en œuvre par divers progiciels de calcul statistique (par exemple, SAS, R 4,6). Nous présentons ici une version qui est étroitement liée à la statistique du test du chi carré et qui compare le nombre observé au nombre attendu d’événements à chaque point temporel de la période de suivi.

Exemple:

Un petit essai clinique est mené pour comparer deux traitements combinés chez des patients atteints d’un cancer gastrique avancé. Vingt participants atteints d’un cancer gastrique de stade IV qui consentent à participer à l’essai sont répartis au hasard pour recevoir une chimiothérapie avant la chirurgie ou une chimiothérapie après la chirurgie. Le principal résultat est le décès et les participants sont suivis jusqu’à 48 mois (4 ans) après leur inscription à l’essai. Les expériences des participants dans chaque bras de l’essai sont présentées ci-dessous.

.

Chémothérapie avant la chirurgie			Chémothérapie après la chirurgie
Mois de… décès	Mois du dernier contact		Mois du décès	Mois du dernier contact
8	8		33	48
12	32		28	48
26	20		41	25
14	40			37
21				48
27				25
				43

Six participants du groupe chimiothérapie avant chirurgie meurent au cours du suivi-.suivi, contre trois participants dans le groupe chimiothérapie après chirurgie. Les autres participants de chaque groupe sont suivis pendant un nombre variable de mois, certains jusqu’à la fin de l’étude à 48 mois (dans le groupe chimiothérapie après chirurgie). En utilisant les procédures décrites ci-dessus, nous construisons d’abord des tables de survie pour chaque groupe de traitement en utilisant l’approche de Kaplan-Meier.

Table de vie pour le groupe recevant une chimiothérapie avant chirurgie

.

.

Temps, Mois	Nombre à risque Nt	Nombre de décès Dt	Nombre censuré Ct	Probabilité de survie
0	10			1
8	10	1	1	0.900
12	8	1		0.788
14	7	1		0.675
20	6		1	0.675
21	5	1		0.540
26	4	1		0.405
27	3	1		0.270
32	2		1	0.270
40	1		1	0.270

Tableau de vie pour le groupe recevant une chimiothérapie après chirurgie

.

.

Temps, Mois	Nombre à risque Nt	Nombre de décès Dt	Nombre censuré Ct	Probabilité de survie
0	10			1
25	10		2	1.000
28	8	1		0.875
33	7	1		0.750
37	6		1	0.750
41	5	1		0.600
43	4		1	0.600
48	3		3	0,600

Les deux courbes de survie sont présentées ci-dessous.

Survie dans chaque groupe de traitement

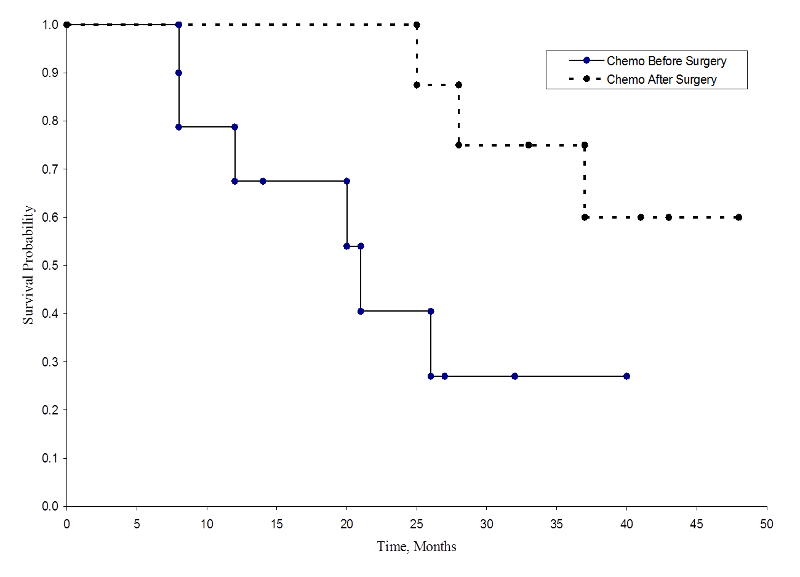
Les probabilités de survie pour le groupe chimiothérapie après chirurgie sont plus élevées que les probabilités de survie pour le groupe chimiothérapie avant chirurgie, suggérant un bénéfice de survie. Cependant, ces courbes de survie sont estimées à partir de petits échantillons. Pour comparer la survie entre les groupes, nous pouvons utiliser le test du log rank. L’hypothèse nulle est qu’il n’y a pas de différence de survie entre les deux groupes ou qu’il n’y a pas de différence entre les populations dans la probabilité de décès à un moment donné. Le test du log rank est un test non paramétrique qui ne fait aucune hypothèse sur les distributions de survie. En substance, le test du log rank compare le nombre d’événements observés dans chaque groupe à ce qui serait attendu si l’hypothèse nulle était vraie (c’est-à-dire si les courbes de survie étaient identiques), si les courbes de survie étaient identiques).

H0 : Les deux courbes de survie sont identiques (ou S1t = S2t) versus H1 : Les deux courbes de survie ne sont pas identiques (ou S1t ≠ S2t, à tout moment t) (α=0,05).

La statistique du log rank est approximativement distribuée comme une statistique de test du chi-deux. Il existe plusieurs formes de cette statistique de test, et elles varient en termes de mode de calcul. Nous utilisons la suivante :

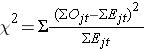
où ΣOjt représente la somme du nombre observé d’événements dans le jème groupe au cours du temps (par exemple, j=1,2) et ΣEjt représente la somme du nombre attendu d’événements dans le jème groupe au cours du temps.

Les sommes des nombres observés et attendus d’événements sont calculées pour chaque temps d’événement et additionnées pour chaque groupe de comparaison. La statistique du log rank a des degrés de liberté égaux à k-1, où k représente le nombre de groupes de comparaison. Dans cet exemple, k=2 donc la statistique de test a 1 degré de liberté.

Pour calculer la statistique de test, nous avons besoin du nombre observé et attendu d’événements à chaque temps d’événement. Le nombre observé d’événements provient de l’échantillon et le nombre attendu d’événements est calculé en supposant que l’hypothèse nulle est vraie (c’est-à-dire que les courbes de survie sont identiques).

Pour générer les nombres attendus d’événements, nous organisons les données dans une table de survie avec des lignes représentant chaque temps d’événement, indépendamment du groupe dans lequel l’événement s’est produit. Nous gardons également la trace de l’affectation des groupes. Nous estimons ensuite la proportion d’événements qui se produisent à chaque moment (Ot/Nt) en utilisant les données des deux groupes combinés, en supposant qu’il n’y a pas de différence dans la survie (c’est-à-dire en supposant que l’hypothèse nulle est vraie). Nous multiplions ces estimations par le nombre de participants à risque à ce moment-là dans chacun des groupes de comparaison (N1t et N2t pour les groupes 1 et 2 respectivement).

Spécifiquement, nous calculons pour chaque temps d’événement t, le nombre à risque dans chaque groupe, Njt (par exemple, où j indique le groupe, j=1, 2) et le nombre d’événements (décès), Ojt ,dans chaque groupe. Le tableau ci-dessous contient les informations nécessaires pour effectuer le test du log rank afin de comparer les courbes de survie ci-dessus. Le groupe 1 représente le groupe chimiothérapie avant chirurgie, et le groupe 2 représente le groupe chimiothérapie après chirurgie.

Données pour le test du log rank pour comparer les courbes de survie

.

Temps, Mois	Nombre à risque dans le groupe 1 N1t	Nombre à risque dans le groupe 2 N2t	Nombre d’événements (décès) dans le groupe 1 O1t	Nombre. d’événements (décès) dans le groupe 2 O2t
8	10	10	1	0
12	8	10	1	0
14	7	10	1	0
21	5	10	1	0
26	4	8	1	0
27	3	8	1	0
28	2	8	0	1
33	1	7	0	1
41	0	5	0	1

Nous totalisons ensuite le nombre à risque, Nt = N1t+N2t, à chaque temps d’événement et le nombre d’événements observés (décès), Ot = O1t+O2t, à chaque temps d’événement. Nous calculons ensuite le nombre attendu d’événements dans chaque groupe. Le nombre attendu d’événements est calculé à chaque temps d’événement comme suit :

E1t = N1t*(Ot/Nt) pour le groupe 1 et E2t = N2t*(Ot/Nt) pour le groupe 2. Les calculs sont présentés dans le tableau ci-dessous.

Nombre attendu d’événements dans chaque groupe

.

.

Temps, Mois	Nombre à risque dans le groupe 1 N1t	Nombre à risque dans le groupe 2 N2t	Nombre total à risque Nt .	Nombre d’événements dans le groupe 1 O1t	Nombre d’événements dans le groupe 2 O2t	Nombre total d’événements Ot	Nombre attendu d’événements dans Groupe 1 E1t = N1t*(Ot/Nt)	Nombre attendu d’événements dans Groupe 2 E2t = N2t*(Ot/Nt)
8	10	10	20	1	0	1	0.500	0.500
12	8	10	18	1	0	1	0.444	0.556
14	7	10	17	1	0	1	0.412	0.588
21	5	10	15	1	0	1	0.333	0.667
26	4	8	12	1	0	1	0.333	0.667
27	3	8	11	1	0	1	0.273	0.727
28	2	8	10	0	1	1	0.200	0.800
33	1	7	8	0	1	1	0.125	0.875
41	0	5	5	0	1	1	0.000	1,000

Nous additionnons ensuite les nombres observés d’événements dans chaque groupe (∑O1t et ΣO2t) et les nombres attendus d’événements dans chaque groupe (ΣE1t et ΣE2t) en fonction du temps. Ils sont présentés dans la ligne inférieure du tableau suivant ci-dessous.

Nombre total observé et attendu d’observés dans chaque groupe

.

.

Temps, Mois	Nombre à risque dans le groupe 1 N1t	Nombre à risque dans le groupe 2 N2t	Nombre total à risque Nt .	Nombre d’événements dans le groupe 1 O1t	Nombre d’événements dans le groupe 2 O2t	Nombre total d’événements Ot	Nombre attendu d’événements dans Groupe 1 E1t = N1t*(Ot/Nt)	Nombre attendu d’événements dans Groupe 2 E2t = N2t*(Ot/Nt)
8	10	10	20	1	0	1	0.500	0.500
12	8	10	18	1	0	1	0.444	0.556
14	7	10	17	1	0	1	0.412	0.588
21	5	10	15	1	0	1	0.333	0.667
26	4	8	12	1	0	1	0.333	0.667
27	3	8	11	1	0	1	0.273	0.727
28	2	8	10	0	1	1	0.200	0.800
33	1	7	8	0	1	1	0.125	0.875
41	0	5	5	0	1	1	0.000	1.000
				6	3		2.620	6,380

Nous pouvons maintenant calculer la statistique de test :

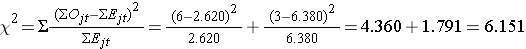
La statistique de test est approximativement distribuée comme un chi-deux avec 1 degré de liberté. Ainsi, la valeur critique du test peut être trouvée dans le tableau des valeurs critiques de la distribution Χ2.

Pour ce test, la règle de décision est de rejeter H0 si Χ2 > 3,84. Nous observons Χ2 = 6,151, ce qui dépasse la valeur critique de 3,84. Par conséquent, nous rejetons H0. Nous avons une preuve significative, α=0,05, pour montrer que les deux courbes de survie sont différentes.

Exemple:

Un investigateur souhaite évaluer l’efficacité d’une intervention brève pour prévenir la consommation d’alcool pendant la grossesse. Les femmes enceintes ayant des antécédents de forte consommation d’alcool sont recrutées dans l’étude et randomisées pour recevoir soit l’intervention brève axée sur l’abstinence d’alcool, soit les soins prénataux standard. Le résultat recherché est la rechute dans la consommation d’alcool. Les femmes sont recrutées dans l’étude à environ 18 semaines de gestation et suivies tout au long de la grossesse jusqu’à l’accouchement (environ 39 semaines de gestation). Les données sont présentées ci-dessous et indiquent si les femmes rechutent et, dans l’affirmative, la date de leur premier verre, mesurée en nombre de semaines à partir de la randomisation. Pour les femmes qui ne rechutent pas, nous enregistrons le nombre de semaines à partir de la randomisation où elles n’ont pas consommé d’alcool.

.

.

Soins prénataux standard			Intervention brève
Rechute	Pas de rechute		Rechute	Pas de rechute
19	20		16	21
6	19		21	15
5	17		7	18
4	14			18
				5

La question d’intérêt est de savoir s’il y a une différence dans le temps de rechute entre les femmes assignées aux soins prénataux standards par rapport à celles assignées à l’intervention brève.

• Etape 1.

Mettre en place des hypothèses et déterminer le niveau de signification.

H0 : Le temps sans rechute est identique entre les groupes versus

H1 : Le temps sans rechute n’est pas identique entre les groupes (α=0,05)

• Etape 2.

Sélectionner la statistique de test appropriée.

La statistique de test pour le test du log rank est

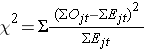
• Étape 3.

Mettre en place la règle de décision.

La statistique de test suit une distribution du chi carré, et nous trouvons donc la valeur critique dans le tableau des valeurs critiques pour la distribution Χ2) pour df=k-1=2-1=1 et α=0,05. La valeur critique est de 3,84 et la règle de décision est de rejeter H0 si Χ2 > 3,84.

• Étape 4.

Calculer la statistique de test.

Pour calculer la statistique de test, nous organisons les données selon les temps d’événement (rechute) et déterminons le nombre de femmes à risque dans chaque groupe de traitement et le nombre qui rechute à chaque temps de rechute observé. Dans le tableau suivant, le groupe 1 représente les femmes qui reçoivent des soins prénataux standard et le groupe 2 représente les femmes qui reçoivent l’intervention brève.

.

Temps, Semaines	Nombre à risque – groupe 1 N1t	Nombre à risque – groupe 2 N2t	Nombre de rechutes – groupe 1 O1t	Nombre de rechutes – groupe 2 O2t	. Groupe 2 O2t
4	8	8	1	0
5	7	8	1	0
6	6	7	1	0
7	5	7	0	1
16	4	5	0	1
19	3	2	1	0
21	0	2	0	1

Nous totalisons ensuite le nombre à risque, 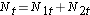, à chaque temps d’événement, le nombre d’événements observés (rechutes), 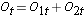, à chaque temps d’événement et déterminons le nombre attendu de rechutes dans chaque groupe à chaque temps d’événement en utilisan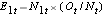t et .

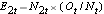Nous additionnons ensuite les nombres observés d’événements dans chaque groupe (ΣO1t et ΣO2t) et les nombres attendus d’événements dans chaque groupe (ΣE1t et ΣE2t) au fil du temps. Les calculs pour les données de cet exemple sont présentés ci-dessous.

.

Temps, Semaines	Nombre à risque groupe 1 N1t	Nombre à risque groupe 2 N2t	Nombre total à risque Nt	. Nombre de rechutes Groupe 1 O1t	Nombre de rechutes Groupe 2 O2t	Nombre total de rechutes . Ot	Nombre attendu de rechutes dans le groupe 1	Nombre attendu de rechutes dans le groupe 2
4	8	8	16	1	0	1	0.500	0.500
5	7	8	15	1	0	1	0.467	0.533
6	6	7	13	1	0	1	0.462	0.538
7	5	7	12	0	1	1	0.417	0.583
16	4	5	9	0	1	1	0.444	0.556
19	3	2	5	1	0	1	0.600	0.400
21	0	2	2	0	1	1	0.000	1.000
				4	3		2.890	4.110

Nous calculons maintenant la statistique de test :

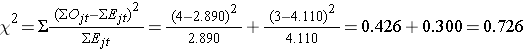
• Étape 5.

Conclusion. Ne pas rejeter H0 parce que 0,726 < 3,84. Nous n’avons pas de preuve statistiquement significative à α=0,05, pour montrer que le temps de rechute est différent entre les groupes.

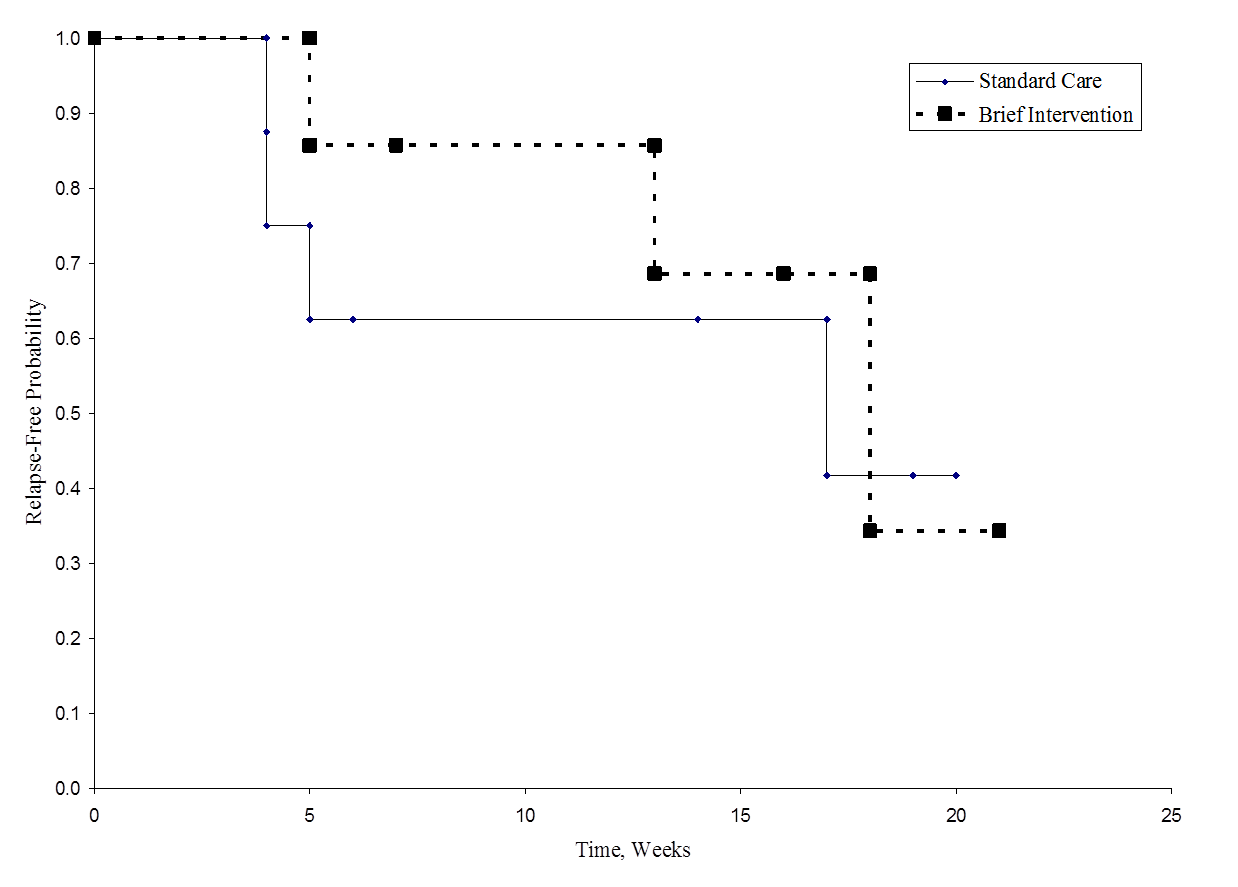
La figure ci-dessous montre la survie (temps sans rechute) dans chaque groupe. Remarquez que les courbes de survie ne montrent pas beaucoup de séparation, ce qui correspond aux résultats non significatifs du test d’hypothèse.

Temps sans rechute dans chaque groupe

Comme nous l’avons noté, il existe plusieurs variantes de la statistique du log rank. Certains progiciels de calcul statistique utilisent la statistique suivante pour le test du log rank afin de comparer deux groupes indépendants :

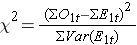
où ΣO1t est la somme du nombre observé d’événements dans le groupe 1, et ΣE1t est la somme du nombre attendu d’événements dans le groupe 1 pris sur tous les temps d’événements. Le dénominateur est la somme des variances des nombres attendus d’événements à chaque temps d’événement, qui est calculée comme suit :

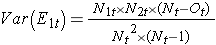
Il existe d’autres versions de la statistique du log rank ainsi que d’autres tests pour comparer les fonctions de survie entre groupes indépendants7-9. Par exemple, un test populaire est le test de Wilcoxon modifié qui est sensible à des différences plus importantes dans les risques plus tôt que plus tard dans le suivi.10

retour en haut | page précédente | page suivante

.