Avant de répondre à notre question racine c’est-à-dire. Comment formuler mathématiquement les problèmes de RL (en utilisant le MDP), nous devons développer notre intuition sur :

• La relation Agent-Environnement
• Propriété de Markov
• Processus de Markov et chaînes de Markov
• Processus de récompense de Markov (MRP)
• Équation de Bellman
• Processus de récompense de Markov

Atteignez votre café et ne vous arrêtez pas avant d’être fier !🧐

La relation agent-environnement

D’abord, regardons quelques définitions formelles :

Agent : programmes logiciels qui prennent des décisions intelligentes et ce sont les apprenants dans le RL. Ces agents interagissent avec l’environnement par des actions et reçoivent des récompenses en fonction de leurs actions.

Environnement :C’est la démonstration du problème à résoudre.Maintenant, nous pouvons avoir un environnement réel ou un environnement simulé avec lequel notre agent va interagir.

État : C’est la position des agents à un pas de temps spécifique dans l’environnement.Ainsi,chaque fois qu’un agent effectue une action, l’environnement lui donne une récompense et un nouvel état où l’agent a atteint en effectuant l’action.

Tout ce que l’agent ne peut pas changer arbitrairement est considéré comme faisant partie de l’environnement. En termes simples, les actions peuvent être toute décision que nous voulons que l’agent apprenne et l’état peut être tout ce qui peut être utile dans le choix des actions. Nous ne supposons pas que tout dans l’environnement est inconnu de l’agent, par exemple, le calcul de la récompense est considéré comme une partie de l’environnement même si l’agent sait un peu comment sa récompense est calculée en fonction de ses actions et des états dans lesquels elles sont prises. Cela est dû au fait que les récompenses ne peuvent pas être modifiées arbitrairement par l’agent. Parfois, l’agent peut être parfaitement conscient de son environnement mais éprouver des difficultés à maximiser la récompense, comme nous pouvons savoir comment jouer au Rubik’s cube mais ne pas réussir à le résoudre. Ainsi, nous pouvons dire sans risque que la relation agent-environnement représente la limite du contrôle de l’agent et non sa connaissance.

La propriété de Markov

Transition : Passer d’un état à un autre est appelé Transition.

Probabilité de transition : La probabilité que l’agent passe d’un état à un autre est appelée probabilité de transition.

La propriété de Markov énonce que :

« Le futur est indépendant du passé étant donné le présent »

Mathématiquement, nous pouvons exprimer cette affirmation comme suit :

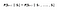
S désigne l’état actuel de l’agent et s désigne l’état suivant. Ce que cette équation signifie, c’est que la transition de l’état S à S est entièrement indépendante du passé. Ainsi, le RHS de l’équation signifie la même chose que le LHS si le système a une propriété de Markov. Intuitivement, cela signifie que notre état actuel capture déjà l’information des états passés.

Probabilité de transition d’état :

Comme nous connaissons maintenant la probabilité de transition, nous pouvons définir la probabilité de transition d’état comme suit :

Pour un état de Markov de S à S c’est-à-dire. tout autre état successeur , la probabilité de transition d’état est donnée par

Nous pouvons formuler la probabilité de transition d’état en une matrice de probabilité de transition d’état par :

Chaque ligne de la matrice représente la probabilité de passer de notre état d’origine ou de départ à tout état successeur.La somme de chaque ligne est égale à 1.

Processus de Markov ou chaînes de Markov

Le processus de Markov est le processus aléatoire sans mémoire c’est-à-dire une séquence d’un état aléatoire S,S,….S avec une propriété de Markov.C’est donc essentiellement une séquence d’états avec la propriété de Markov.Il peut être défini en utilisant un ensemble d’états(S) et une matrice de probabilité de transition (P).La dynamique de l’environnement peut être entièrement définie en utilisant les états(S) et la matrice de probabilité de transition(P).

Mais que signifie processus aléatoire ?

Pour répondre à cette question regardons un exemple:

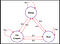
Les arêtes de l’arbre désignent la probabilité de transition. A partir de cette chaîne, prenons un échantillon. Maintenant, supposons que nous dormions et que, selon la distribution de probabilité, il y a 0,6 chance que nous courions et 0,2 chance que nous dormions davantage et encore 0,2 chance que nous mangions une glace. De même, nous pouvons penser à d’autres séquences que nous pouvons échantillonner à partir de cette chaîne.

Quelques échantillons de la chaîne :

• Dormir – Courir – Glace – Dormir
• Dormir – Glace – Glace – Courir

Dans les deux séquences ci-dessus, ce que nous voyons est que nous obtenons un ensemble aléatoire d’États(S) (c’est-à-dire Dormir,Glace,Dormir ) chaque fois que nous exécutons la chaîne.J’espère que l’on comprend maintenant pourquoi le processus de Markov est appelé ensemble aléatoire de séquences.

Avant d’aborder le processus de Markov de récompense, examinons quelques concepts importants qui nous aideront à comprendre les MRP.

Récompense et retours

Les récompenses sont les valeurs numériques que l’agent reçoit en effectuant une action à un ou plusieurs états de l’environnement. La valeur numérique peut être positive ou négative en fonction des actions de l’agent.

Dans l’apprentissage par renforcement, on se soucie de maximiser la récompense cumulative (toutes les récompenses que l’agent reçoit de l’environnement) au lieu de, la récompense que l’agent reçoit de l’état actuel(aussi appelée récompense immédiate). Cette somme totale de récompense que l’agent reçoit de l’environnement est appelée rendement.

Nous pouvons définir les retours comme :

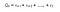
r est la récompense reçue par l’agent au pas de temps t lors de l’exécution d’une action(a) pour passer d’un état à un autre. De même, r est la récompense reçue par l’agent au pas de temps t en réalisant une action pour passer à un autre état. Et, r est la récompense reçue par l’agent par au dernier pas de temps en effectuant une action pour passer à un autre état.

Tâches épisodiques et continues

Tâches épisodiques : Ce sont les tâches qui ont un état terminal (état final).On peut dire qu’elles ont des états finis. Par exemple, dans les jeux de course, on commence le jeu (on commence la course) et on y joue jusqu’à la fin du jeu (la course se termine !). C’est ce qu’on appelle un épisode. Une fois que nous redémarrons le jeu, il repartira d’un état initial et donc, chaque épisode est indépendant.

Tâches continues : Ce sont les tâches qui n’ont pas de fin c’est-à-dire qu’elles n’ont pas d’état terminal.Ces types de tâches ne se termineront jamais.Par exemple, Apprendre à coder !

Maintenant, il est facile de calculer les rendements des tâches épisodiques car elles finiront par se terminer mais qu’en est-il des tâches continues, car cela continuera à l’infini. Les rendements de la somme jusqu’à l’infini ! Alors, comment définir les rendements des tâches continues ?

C’est là que nous avons besoin du facteur d’actualisation (ɤ).

Facteur d’actualisation (ɤ) : Il détermine l’importance à accorder à la récompense immédiate et aux récompenses futures. Cela nous aide essentiellement à éviter l’infini comme récompense dans les tâches continues. Sa valeur est comprise entre 0 et 1. Une valeur de 0 signifie que l’on accorde plus d’importance à la récompense immédiate et une valeur de 1 signifie que l’on accorde plus d’importance aux récompenses futures. Dans la pratique, un facteur d’actualisation de 0 n’apprendra jamais car il ne prend en compte que la récompense immédiate et un facteur d’actualisation de 1 continuera à prendre en compte les récompenses futures, ce qui peut mener à l’infini. Par conséquent, la valeur optimale du facteur d’actualisation se situe entre 0,2 et 0,8.

Donc, nous pouvons définir les rendements en utilisant le facteur d’escompte comme suit :(Disons que c’est l’équation 1 ,car nous allons utiliser cette équation plus tard pour dériver l’équation de Bellman)

Comprenons cela avec un exemple,Supposons que vous vivez dans un endroit où vous faites face à une pénurie d’eau, donc si quelqu’un vient vous dire qu’il vous donnera 100 litres d’eau !(assumez s’il vous plaît !) pour les 15 prochaines heures en fonction d’un certain paramètre (ɤ).Regardons deux possibilités : (Disons que c’est l’équation 1 ,car nous allons utiliser cette équation dans la suite pour dériver l’équation de Bellman)

L’une avec le facteur d’actualisation (ɤ) 0.8 :

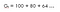
Cela signifie que nous devrions attendre jusqu’à la 15e heure car la diminution n’est pas très significative , donc cela vaut toujours la peine d’aller jusqu’au bout.Cela signifie que nous sommes également intéressés par les récompenses futures.Donc, si le facteur d’actualisation est proche de 1, alors nous ferons un effort pour aller jusqu’à la fin car les récompenses ont une importance significative.

Deuxièmement, avec le facteur d’actualisation (ɤ) 0,2 :

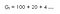
Cela signifie que nous sommes plus intéressés par les récompenses précoces car les récompenses deviennent significativement faibles à l’heure.Donc, nous pourrions ne pas vouloir attendre jusqu’à la fin (jusqu’à la 15e heure) car cela ne vaudrait rien.Donc, si le facteur d’actualisation est proche de zéro, alors les récompenses immédiates sont plus importantes que le futur.

Alors quelle valeur du facteur d’actualisation utiliser ?

Cela dépend de la tâche pour laquelle nous voulons entraîner un agent. Supposons que, dans une partie d’échecs, le but est de vaincre le roi de l’adversaire. Si nous donnons de l’importance aux récompenses immédiates comme une récompense sur la défaite d’un pion de n’importe quel joueur adverse, alors l’agent apprendra à réaliser ces sous-objectifs peu importe si ses joueurs sont également vaincus. Ainsi, dans cette tâche, les récompenses futures sont plus importantes. Dans certains, nous pourrions préférer utiliser des récompenses immédiates comme l’exemple de l’eau que nous avons vu plus tôt.

Processus de récompense de Markov

Jusqu’à présent, nous avons vu comment la chaîne de Markov définissait la dynamique d’un environnement en utilisant un ensemble d’états(S) et une matrice de probabilité de transition(P).Mais, nous savons que l’apprentissage par renforcement est tout au sujet du but de maximiser la récompense.Donc, ajoutons la récompense à notre chaîne de Markov.Cela nous donne le processus de récompense de Markov.

Processus de récompense de Markov : Comme son nom l’indique, les MDP sont les chaînes de Markov avec jugement de valeurs.En gros, nous obtenons une valeur de chaque état dans lequel se trouve notre agent.

Mathématiquement, nous définissons le processus de récompense de Markov comme :

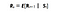
Ce que cette équation signifie, c’est combien de récompense (Rs) nous obtenons d’un état particulier S. Cela nous indique la récompense immédiate de cet état particulier dans lequel se trouve notre agent. Comme nous allons le voir dans l’histoire suivante, nous maximisons ces récompenses pour chaque état dans lequel se trouve notre agent. En termes simples, maximiser la récompense cumulative que nous obtenons de chaque état.

Nous définissons le MRP comme (S,P,R,ɤ) ,où :

• S est un ensemble d’états,
• P est la matrice de probabilité de transition,
• R est la fonction de récompense , que nous avons vue précédemment,
• ɤ est le facteur d’actualisation

Processus de décision de Markov

Maintenant, développons notre intuition pour l’équation de Bellman et le processus de décision de Markov.

Fonction de politique et fonction de valeur

La fonction de valeur détermine combien il est bon pour l’agent d’être dans un état particulier. Bien sûr, pour déterminer à quel point il sera bon d’être dans un état particulier, il faut que cela dépende de certaines actions qu’il va entreprendre. C’est là qu’intervient la politique. Une politique définit les actions à effectuer dans un état particulier s.

Une politique est une fonction simple, qui définit une distribution de probabilité sur les actions (a∈ A) pour chaque état (s ∈ S). Si un agent au temps t suit une politique π alors π(a|s) est la probabilité que l’agent avec prendre l’action (a ) à un pas de temps particulier (t).Dans l’apprentissage par renforcement, l’expérience de l’agent détermine le changement de politique. Mathématiquement, une politique est définie comme suit :

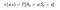
Maintenant, comment on trouve la valeur d’un état.La valeur de l’état s, lorsque l’agent suit une politique π qui est dénotée par vπ(s) est le rendement attendu en partant de s et en suivant une politique π pour les états suivants,jusqu’à atteindre l’état terminal.Nous pouvons formuler cela comme :(Cette fonction est également appelée fonction État-valeur)

Cette équation nous donne les rendements attendus en partant de l’état(s) et en allant vers les états successifs par la suite, avec la politique π. Une chose à noter est que les retours que nous obtenons sont stochastiques alors que la valeur d’un état n’est pas stochastique. Il s’agit de l’espérance des rendements à partir de l’état de départ s et ensuite, à tout autre état. Notez également que la valeur de l’état terminal (s’il existe) est égale à zéro. Voyons un exemple :

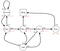
Supposons que notre état de départ soit la classe 2, et que nous passions à la classe 3 puis à la passe puis au sommeil.En bref, classe 2 > classe 3 > passe > sommeil.

Notre rendement attendu est avec un facteur d’escompte de 0,5:

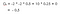
Note:C’est -2 + (-2 * 0.5) + 10 * 0,25 + 0 au lieu de -2 * -2 * 0,5 + 10 * 0,25 + 0.Alors la valeur de la classe 2 est -0,5 .

Équation de Bellman pour la fonction de valeur

L’équation de Bellman nous aide à trouver les politiques optimales et la fonction de valeur.Nous savons que notre politique change avec l’expérience donc nous aurons une fonction de valeur différente selon les différentes politiques.La fonction de valeur optimale est celle qui donne une valeur maximale par rapport à toutes les autres fonctions de valeur.

L’équation de Bellman stipule que la fonction de valeur peut être décomposée en deux parties :

• Récompense immédiate, R
• Valeur actualisée des états successeurs,

Mathématiquement, nous pouvons définir l’équation de Bellman comme :

Comprenons ce que dit cette équation à l’aide d’un exemple :

Supposons qu’il y ait un robot dans un certain état (s) et qu’il se déplace ensuite de cet état vers un autre état (s’). Maintenant, la question est de savoir s’il était bon pour le robot d’être dans cet état (s). En utilisant l’équation de Bellman, on peut que c’est l’espérance de récompense qu’il a obtenue en quittant l’état (s) plus la valeur de l’état (s’) vers lequel il s’est déplacé.

Regardons un autre exemple :

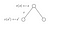
Nous voulons connaître la valeur de l’état s.La valeur de l’état s est la récompense que nous avons obtenue en quittant cet état, plus la valeur actualisée de l’état sur lequel nous avons atterri, multipliée par la probabilité de transition que nous y entrions.

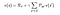
L’équation ci-dessus peut être exprimée sous forme de matrice comme suit :

Où v est la valeur de l’état dans lequel nous étions, qui est égale à la récompense immédiate plus la valeur actualisée de l’état suivant multipliée par la probabilité de passer dans cet état.

La complexité du temps d’exécution pour ce calcul est O(n³). Par conséquent, ce n’est clairement pas une solution pratique pour résoudre les plus grands MRP (même chose pour les MDP, aussi).Dans les Blogs suivants, nous examinerons des méthodes plus efficaces comme la programmation dynamique (itération de valeur et itération de politique), les méthodes de Monte-Claro et le TD-Learning.

Nous allons parler de l’équation de Bellman de manière beaucoup plus détaillée dans la prochaine histoire.

Qu’est-ce que le processus de décision de Markov ?

Processus de décision de Markov : C’est un processus de récompense de Markov avec des décisions.Tout est identique comme MRP mais maintenant nous avons une agence réelle qui prend des décisions ou prend des actions.

C’est un tuple de (S, A, P, R, 𝛾) où :

• S est un ensemble d’états,
• A est l’ensemble des actions que l’agent peut choisir de prendre,
• P est la matrice de probabilité de transition,
• R est la récompense accumulée par les actions de l’agent,
• 𝛾 est le facteur d’actualisation.

P et R auront un léger changement en fonction des actions comme suit :

Matrice de probabilité de transition

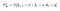
Fonction de récompense

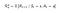
Maintenant, notre fonction de récompense dépend de l’action.

Jusqu’à présent, nous avons parlé d’obtenir une récompense (r) lorsque notre agent passe par un ensemble d’états (s) en suivant une politique π.En fait, dans le processus de décision de Markov (PDM), la politique est le mécanisme qui permet de prendre des décisions .Donc maintenant nous avons un mécanisme qui va choisir de prendre une action.

Les politiques dans un PDM dépendent de l’état actuel.Elles ne dépendent pas de l’histoire.C’est la propriété de Markov.Donc, l’état actuel dans lequel nous sommes caractérise l’histoire.

Nous avons déjà vu combien il est bon pour l’agent d’être dans un état particulier(fonction de valeur d’état).Maintenant, voyons combien il est bon de prendre une action particulière en suivant une politique π à partir de l’état s (fonction de valeur d’action).

Fonction de valeur d’état-action ou fonction Q

Cette fonction spécifie le combien il est bon pour l’agent de prendre une action (a) dans un état (s) avec une politique π.

Mathématiquement, nous pouvons définir la fonction de valeur État-action comme :

Basiquement, elle nous indique la valeur d’effectuer une certaine action (a) dans un état (s) avec une politique π.

Regardons un exemple de processus de décision de Markov :

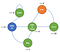
Maintenant, nous pouvons voir qu’il n’y a plus de probabilités.En fait, maintenant notre agent a des choix à faire comme après s’être réveillé ,on peut choisir de regarder netflix ou de coder et déboguer.Bien sûr, les actions de l’agent sont définies par rapport à une certaine politique π et sera obtenir la récompense en conséquence.

.