Bonjour les amis ! Dans cet article, je vais décrire un algorithme utilisé dans le traitement du langage naturel : Latent Semantic Analysis ( LSA ).
Les principales applications de cette méthode susmentionnée sont vastes en linguistique : Comparer les documents dans des espaces de faible dimension (Similarité des documents), Trouver des sujets récurrents à travers les documents (Modélisation des sujets), Trouver des relations entre les termes (Synoymité des textes).

Introduction
Le modèle de l’analyse sémantique latente est une théorie sur la façon dont les représentations de sens
pourraient être apprises à partir de la rencontre de grands échantillons de langage sans indications explicites sur la façon dont il est structuré.
Le problème à la main n’est pas supervisé, c’est-à-dire que nous n’avons pas d’étiquettes ou de catégories fixes assignées au corpus.
Pour extraire et comprendre les modèles à partir des documents, LSA suit intrinsèquement certaines hypothèses :
1) La signification des phrases ou des documents est une somme de la signification de tous les mots qui y apparaissent. Globalement, la signification d’un certain mot est une moyenne de tous les documents dans lesquels il apparaît.
2) LSA suppose que les associations sémantiques entre les mots ne sont pas présentes de manière explicite, mais seulement de manière latente dans le grand échantillon de langage.
Perspective mathématique
L’analyse sémantique latente (LSA) comprend certaines opérations mathématiques pour obtenir un aperçu sur un document. Cet algorithme constitue la base de la modélisation thématique. L’idée centrale est de prendre une matrice de ce que nous avons – documents et termes – et de la décomposer en une matrice document-sujet et une matrice sujet-terme distinctes.
La première étape consiste à générer notre matrice document-terme en utilisant le Vectoriseur Tf-IDF. Elle peut également être construite à l’aide d’un modèle de sac de mots, mais les résultats sont épars et n’apportent aucune signification à la question.
Donné m documents et n mots dans notre vocabulaire, nous pouvons construire une
m × n matrice A dans laquelle chaque ligne représente un document et chaque colonne représente un mot.
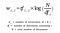
Intuitivement, un terme a un poids important lorsqu’il apparaît fréquemment dans le document mais peu fréquemment dans le corpus.
Nous formons une matrice document-terme, A en utilisant cette méthode de transformation(tf-IDF) pour vectoriser notre corpus. ( D’une manière, que notre modèle ultérieur peut traiter ou évaluer puisque nous ne travaillons pas encore sur les chaînes de caractères !).
Mais il y a un inconvénient subtil, nous ne pouvons rien déduire en observant A, puisque c’est une matrice bruyante et éparse. ( Parfois trop grande pour même être calculée pour les processus ultérieurs).
Puisque la modélisation des sujets est par nature un algorithme non supervisé, nous devons spécifier les sujets latents à l’avance. C’est analogue à K-Means Clustering tel que nous spécifions le nombre de cluster à l’avance.
Dans ce cas, nous effectuons une Approximation à faible rang en utilisant une technique de réduction de la dimensionnalité en utilisant une décomposition en valeur singulière tronquée (SVD).
La décomposition en valeur singulière est une technique d’algèbre linéaire qui factorise toute matrice M en produit de 3 matrices séparées : M=U*S*V, où S est une matrice diagonale des valeurs singulières de M.
La SVD tronquée réduit la dimensionnalité en ne sélectionnant que les t plus grandes valeurs singulières et en ne conservant que les t premières colonnes de U et V. Dans ce cas, t est un hyperparamètre que nous pouvons sélectionner et ajuster pour refléter le nombre de sujets que nous voulons trouver.
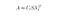
Note : la SVD tronquée fait la réduction de dimensionnalité et non la SVD !

Avec ces vecteurs de documents et vecteurs de termes, nous pouvons maintenant facilement appliquer des mesures telles que la similarité en cosinus pour évaluer :
- la similarité de différents documents
- la similarité de différents mots
- la similarité de termes (ou « requêtes ») et de documents (ce qui devient utile en recherche d’information, lorsque nous voulons récupérer les passages les plus pertinents pour notre requête de recherche).
Marques finales
Cet algorithme est principalement utilisé dans diverses tâches basées sur le NLP et est la base de méthodes plus robustes comme le LSA probabiliste et l’allocation de Dirichlet latente (LDA).
Kushal Vala, Junior Data Scientist at Datametica Solutions Pvt Ltd
.