
Bien que, comme mentionné dans la section Analyse du flux de signaux, une certaine forme d’analyse du flux de signaux est la façon la plus générale de traiter l’amplificateur à contre-réaction négative, la représentation sous forme de deux deux-ports est l’approche la plus souvent présentée dans les manuels et est présentée ici. Elle conserve une partition de circuit à deux blocs de l’amplificateur, mais permet aux blocs d’être bilatéraux. Certains inconvénients de cette méthode sont décrits à la fin.
Les amplificateurs électroniques utilisent le courant ou la tension comme entrée et sortie, donc quatre types d’amplificateurs sont possibles (l’une des deux entrées possibles avec l’une des deux sorties possibles). Voir la classification des amplificateurs. L’objectif de l’amplificateur à rétroaction peut être l’un quelconque des quatre types d’amplificateur et n’est pas nécessairement du même type que l’amplificateur en boucle ouverte, qui peut lui-même être l’un quelconque de ces types. Ainsi, par exemple, un amplificateur op (amplificateur de tension) peut être agencé pour faire un amplificateur de courant à la place.
Les amplificateurs à rétroaction négative de tout type peuvent être mis en œuvre en utilisant des combinaisons de réseaux à deux ports. Il existe quatre types de réseaux à deux ports, et le type d’amplificateur souhaité dicte le choix des deux ports et la sélection de l’une des quatre topologies de connexion différentes présentées dans le schéma. Ces connexions sont généralement appelées connexions série ou shunt (parallèles). Dans le diagramme, la colonne de gauche montre les entrées shunt ; la colonne de droite montre les entrées série. La rangée supérieure montre les sorties en série, la rangée inférieure les sorties en dérivation. Les différentes combinaisons de connexions et de deux ports sont répertoriées dans le tableau ci-dessous.
| Type d’amplificateur de rétroaction | Connexion d’entrée | Connexion de sortie | Rétroaction idéale | Rétroaction à deux-port |
|---|---|---|---|---|
| Courant | Shunt | Série | CCCS | g-paramètre |
| Transrésistance | Shunt | Shunt | CCVS | y-paramètre |
| Transconductance | Série | Série | VCCS | z-paramètre |
| Tension | Série | Shunt | VCVS | h-paramètre |
Par exemple, pour un amplificateur à rétroaction en courant, le courant de la sortie est échantillonné pour la rétroaction et combiné au courant à l’entrée. Par conséquent, la rétroaction est idéalement réalisée à l’aide d’une source de courant (sortie) contrôlée par le courant (CCCS), et sa réalisation imparfaite à l’aide d’un réseau à deux ports doit également incorporer un CCCS, c’est-à-dire que le choix approprié pour le réseau de rétroaction est un g-paramètre à deux ports. On présente ici la méthode à deux ports utilisée dans la plupart des manuels, en utilisant le circuit traité dans l’article sur le modèle de gain asymptotique.

La figure 3 montre un amplificateur à deux transistors avec une résistance de rétroaction Rf. Le but est d’analyser ce circuit pour trouver trois éléments : le gain, l’impédance de sortie en regardant l’amplificateur depuis la charge, et l’impédance d’entrée en regardant l’amplificateur depuis la source.
- Remplacement du réseau de rétroaction par un deux-portesModifier
- Circuit à petit signalEdit
- Gain en boucle ouverte chargéEdit
- Gain avec rétroactionEdit
- Résistances d’entrée et de sortieEdit
- Contexte de la détermination de la résistanceEdit
- Application à l’amplificateur d’exempleModifier
- Tension de charge et courant de chargeEdit
- Le bloc amplificateur principal est-il à deux ports ? Editer
Remplacement du réseau de rétroaction par un deux-portesModifier
La première étape est le remplacement du réseau de rétroaction par un deux-portes. Quels sont exactement les composants qui entrent dans le deux-port ?
Du côté de l’entrée du deux-port, nous avons Rf. Si la tension du côté droit de Rf change, cela change le courant dans Rf qui est soustrait du courant entrant dans la base du transistor d’entrée. C’est-à-dire que le côté d’entrée du deux ports est une source de courant dépendante contrôlée par la tension au sommet de la résistance R2.
On pourrait dire que le deuxième étage de l’amplificateur est juste un suiveur de tension, transmettant la tension au collecteur du transistor d’entrée au sommet de R2. Autrement dit, le signal de sortie contrôlé est en réalité la tension au collecteur du transistor d’entrée. Ce point de vue est légitime, mais l’étage suiveur de tension devient alors une partie du réseau de rétroaction. Cela rend l’analyse de la rétroaction plus compliquée.
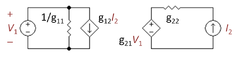
Un autre point de vue est que la tension au sommet de R2 est fixée par le courant d’émetteur du transistor de sortie. Cette vue conduit à un réseau de rétroaction entièrement passif composé de R2 et Rf. La variable contrôlant la rétroaction est le courant de l’émetteur, la rétroaction est donc une source de courant contrôlée par le courant (CCCS). Nous recherchons parmi les quatre réseaux à deux ports disponibles et nous constatons que le seul à posséder une CCCS est le réseau à deux ports à paramètre g, illustré à la figure 4. La tâche suivante consiste à sélectionner les paramètres g de manière à ce que le réseau à deux ports de la figure 4 soit électriquement équivalent à la section L composée de R2 et Rf. Cette sélection est une procédure algébrique réalisée très simplement en examinant deux cas individuels : le cas avec V1 = 0, qui fait du VCVS du côté droit du double port un court-circuit ; et le cas avec I2 = 0, qui fait du CCCS du côté gauche un circuit ouvert. L’algèbre dans ces deux cas est simple, beaucoup plus facile que de résoudre pour toutes les variables à la fois. Le choix des paramètres g qui font que la section à deux ports et la section en L se comportent de la même façon est indiqué dans le tableau ci-dessous.
| g11 | g12 | g21 | g22 |
|---|---|---|---|
1 R f + R 2 {\displaystyle {\frac {1}{R_{\mathrm {f} }+R_{2}}}}
 |
– R 2 R 2 + R f {\displaystyle -{\frac {R_{2}}{R_{2}+R_{\mathrm {f} }}}}
 |
R 2 R 2 + R f {\displaystyle -{frac {R_{2}}{R_{2}+R_{\mathrm {f} }}}}
 |
R 2 / / R f {\displaystyle R_{2}//R_{\mathrm {f} }\ }
 |
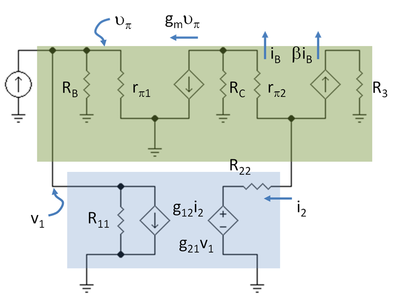
Circuit à petit signalEdit
L’étape suivante consiste à dessiner le schéma à petit signal pour l’amplificateur avec le deux-port en place en utilisant le modèle hybride-pi pour les transistors. La figure 5 montre le schéma avec la notation R3 = RC2 // RL et R11 = 1 / g11, R22 = g22.
Gain en boucle ouverte chargéEdit
La figure 3 indique le nœud de sortie, mais pas le choix de la variable de sortie. Un choix utile est la sortie de courant de court-circuit de l’amplificateur (conduisant au gain de courant de court-circuit). Comme cette variable mène simplement à l’un des autres choix (par exemple, la tension de charge ou le courant de charge), le gain de courant de court-circuit est trouvé ci-dessous.
D’abord, le gain de boucle ouverte chargée est trouvé. La rétroaction est désactivée en réglant g12 = g21 = 0. L’idée est de trouver de combien le gain de l’amplificateur est modifié à cause des résistances du réseau de rétroaction par elles-mêmes, avec la rétroaction désactivée. Ce calcul est assez facile car R11, RB et rπ1 sont tous en parallèle et v1 = vπ. Soit R1 = R11 // RB // rπ1. De plus, i2 = -(β+1) iB. Le résultat pour le gain en courant en boucle ouverte AOL est :
A O L = β i B i S = g m R C ( β β + 1 ) ( R 1 R 22 + r π 2 + R C β + 1 ) . A_{{\mathrm {OL}} style d’affichage }={\frac {\beta i_{\mathrm {B} }}{i_{{\mathrm {S}} }}=g_{m}R_{\mathrm {C} }\left({\frac {R_{beta }{\beta +1}\right)\left({\frac {R_{1}}{R_{22}+{\frac {r_{\pi 2}+R_{\mathrm {C}} }}{\beta +1}}}}\right)\ .}

Gain avec rétroactionEdit
Dans l’approche classique de la rétroaction, la rétroaction représentée par le VCVS (c’est-à-dire g21 v1) est négligée. Cela fait que le circuit de la figure 5 ressemble au schéma-bloc de la figure 1, et le gain avec rétroaction est alors :
A F B = A O L 1 + β F B A O L {\displaystyle A_{\mathrm {FB}}. }={\frac {A_{{\mathrm {OL}} }{1+{\beta }_{\mathrm {FB} }A_{\mathrm {OL} }}}}

A F B = A O L 1 + R 2 R 2 + R f A O L , {\displaystyle A_{\mathrm {FB} }={\frac {A_{\mathrm {OL} }}{1+{\frac {R_{2}}{R_{2}+R_{\mathrm {f}}} }}}A_{\mathrm {OL} }}}, }

où le facteur de rétroaction βFB = -g12. La notation βFB est introduite pour le facteur de rétroaction pour le distinguer du transistor β.
Résistances d’entrée et de sortieEdit

La rétroaction est utilisée pour mieux adapter les sources de signaux à leurs charges. Par exemple, la connexion directe d’une source de tension à une charge résistive peut entraîner une perte de signal due à la division de tension, mais l’interjection d’un amplificateur de contre-réaction peut augmenter la charge apparente vue par la source, et réduire l’impédance apparente du conducteur vue par la charge, évitant ainsi l’atténuation du signal par la division de tension. Cet avantage n’est pas limité aux amplificateurs de tension, mais des améliorations analogues de l’adaptation peuvent être organisées pour les amplificateurs de courant, les amplificateurs de transconductance et les amplificateurs de transrésistance.
Pour expliquer ces effets de la rétroaction sur les impédances, il faut d’abord faire une digression sur la façon dont la théorie à deux ports aborde la détermination de la résistance, puis son application à l’amplificateur en question.
Contexte de la détermination de la résistanceEdit
La figure 6 montre un circuit équivalent pour trouver la résistance d’entrée d’un amplificateur de tension à rétroaction (à gauche) et pour un amplificateur de courant à rétroaction (à droite). Ces montages sont des applications typiques du théorème de Miller.
Dans le cas de l’amplificateur de tension, la tension de sortie βVout du réseau de rétroaction est appliquée en série et avec une polarité opposée à la tension d’entrée Vx parcourant la boucle (mais par rapport à la masse, les polarités sont les mêmes). En conséquence, la tension effective aux bornes de la résistance d’entrée Rin de l’amplificateur et le courant qui la traverse diminuent de sorte que la résistance d’entrée du circuit augmente (on pourrait dire que Rin augmente apparemment). Sa nouvelle valeur peut être calculée en appliquant le théorème de Miller (pour les tensions) ou les lois de base des circuits. Ainsi, la loi de tension de Kirchhoff fournit:
V x = I x R i n + β v o u t , {\displaystyle V_{x}=I_{x}R_{\mathrm {in}} }+\beta v_{\mathrm {out}

où vout = Av vin = Av Ix Rin. En substituant ce résultat dans l’équation ci-dessus et en résolvant pour la résistance d’entrée de l’amplificateur de rétroaction, on obtient :
R i n ( f b ) = V x I x = ( 1 + β A v ) R i n . {\displaystyle R_{\mathrm {in} }(fb)={\frac {V_{x}}{I_{x}}=\left(1+\beta A_{v}\right)R_{\mathrm {in} }\ .}

La conclusion générale de cet exemple et d’un exemple similaire pour le cas de la résistance de sortie est :Une connexion de rétroaction en série à l’entrée (sortie) augmente la résistance d’entrée (sortie) d’un facteur ( 1 + β AOL ), où AOL = gain en boucle ouverte.
D’autre part, pour l’amplificateur de courant, le courant de sortie βIout du réseau de rétroaction est appliqué en parallèle et avec une direction opposée au courant d’entrée Ix. En conséquence, le courant total circulant à travers l’entrée du circuit (pas seulement à travers la résistance d’entrée Rin) augmente et la tension à ses bornes diminue de sorte que la résistance d’entrée du circuit diminue (Rin diminue apparemment). Sa nouvelle valeur peut être calculée en appliquant le théorème dual de Miller (pour les courants) ou les lois de base de Kirchhoff :
I x = V i n R i n + β i o u t . {\displaystyle I_{x}={\frac {V_{\mathrm {in} }}{R_{\mathrm {in}} }}+\beta i_{\mathrm {out} }\ .}

où iout = Ai iin = Ai Vx / Rin. En substituant ce résultat dans l’équation ci-dessus et en résolvant pour la résistance d’entrée de l’amplificateur de rétroaction, on obtient :
R i n ( f b ) = V x I x = R i n ( 1 + β A i ) . {\displaystyle R_{\mathrm {in} }(fb)={\frac {V_{x}}{I_{x}}={\frac {R_{\mathrm {in}} }{\left(1+\beta A_{i}\right)}} .}

La conclusion générale de cet exemple et d’un exemple similaire pour le cas de la résistance de sortie est :Une connexion de rétroaction parallèle à l’entrée (sortie) diminue la résistance d’entrée (sortie) d’un facteur ( 1 + β AOL ), où AOL = gain en boucle ouverte.
Ces conclusions peuvent être généralisées pour traiter des cas avec des commandes arbitraires de Norton ou de Thévenin, des charges arbitraires, et des réseaux généraux de rétroaction à deux ports. Cependant, les résultats dépendent de la représentation de l’amplificateur principal comme étant à deux ports – c’est-à-dire que les résultats dépendent du même courant entrant et sortant des bornes d’entrée, et de même, le même courant qui quitte une borne de sortie doit entrer dans l’autre borne de sortie.
Une conclusion plus large, indépendante des détails quantitatifs, est que la rétroaction peut être utilisée pour augmenter ou diminuer l’impédance d’entrée et de sortie.
Application à l’amplificateur d’exempleModifier
Ces résultats de résistance sont maintenant appliqués à l’amplificateur de la figure 3 et de la figure 5. Le facteur d’amélioration qui réduit le gain, à savoir ( 1 + βFB AOL), décide directement de l’effet de la rétroaction sur les résistances d’entrée et de sortie de l’amplificateur. Dans le cas d’une connexion shunt, l’impédance d’entrée est réduite par ce facteur ; et dans le cas d’une connexion série, l’impédance est multipliée par ce facteur. Cependant, l’impédance qui est modifiée par la rétroaction est l’impédance de l’amplificateur de la figure 5 avec la rétroaction désactivée, et inclut les modifications de l’impédance causées par les résistances du réseau de rétroaction.
Donc, l’impédance d’entrée vue par la source avec la contre-réaction désactivée est Rin = R1 = R11 // RB // rπ1, et avec la contre-réaction activée (mais pas de feedforward)
R i n = R 1 1 + β F B A O L , {\displaystyle R_{\mathrm {in} }={\frac {R_{1}}{1+{\beta }_{\mathrm {FB}} ,}{\c}.} }A_{{\mathrm {OL}} }}}, }

où la division est utilisée car la connexion d’entrée est shuntée : la rétroaction à deux ports est en parallèle avec la source du signal en entrée de l’amplificateur. Un rappel : AOL est le gain en boucle ouverte chargé trouvé ci-dessus, tel que modifié par les résistances du réseau de rétroaction.
L’impédance vue par la charge nécessite une discussion plus approfondie. La charge de la figure 5 est connectée au collecteur du transistor de sortie, et est donc séparée du corps de l’amplificateur par l’impédance infinie de la source de courant de sortie. Par conséquent, la rétroaction n’a aucun effet sur l’impédance de sortie, qui reste simplement RC2 comme on le voit par la résistance de charge RL dans la figure 3.
Si nous voulions plutôt trouver l’impédance présentée à l’émetteur du transistor de sortie (au lieu de son collecteur), qui est connecté en série au réseau de rétroaction, la rétroaction augmenterait cette résistance par le facteur d’amélioration ( 1 + βFB AOL).
Tension de charge et courant de chargeEdit
Le gain dérivé ci-dessus est le gain de courant au collecteur du transistor de sortie. Pour relier ce gain au gain lorsque la tension est la sortie de l’amplificateur, remarquez que la tension de sortie à la charge RL est liée au courant du collecteur par la loi d’Ohm comme vL = iC (RC2 || RL). Par conséquent, le gain de transrésistance vL / iS est trouvé en multipliant le gain de courant par RC2 || RL:
v L i S = A F B ( R C 2 ∥ R L ) . {\displaystyle {\frac {v_{\mathrm {L}] }}{i_{{\mathrm {S}} }}=A_{\mathrm {FB} }(R_{\mathrm {C2}}\parallèle R_{\mathrm {L}})}.

De même, si l’on considère que la sortie de l’amplificateur est le courant dans la résistance de charge RL, la division de courant détermine le courant de charge, et le gain est alors:
i L i S = A F B R C 2 R C 2 + R L . {\displaystyle {\frac {i_{\mathrm {L} }}{i_{{\mathrm {S}} }}=A_{\mathrm {FB} }{\frac {R_{\mathrm {C2}}.}. }}{R_{\mathrm {C2} }+R_{\mathrm {L} }}}\ .}

Le bloc amplificateur principal est-il à deux ports ? Editer

Des inconvénients de l’approche à deux ports suivent, destinés au lecteur attentif.
La figure 7 montre le schéma à petit signal avec l’amplificateur principal et le deux ports de rétroaction dans des cases ombrées. La rétroaction à deux ports satisfait aux conditions de port : au port d’entrée, Iin entre et sort du port, et de même à la sortie, Iout entre et sort.
Le bloc amplificateur principal est-il également à deux ports ? L’amplificateur principal est représenté dans la boîte grisée supérieure. Les connexions de masse sont étiquetées. La figure 7 montre le fait intéressant que l’amplificateur principal ne satisfait pas les conditions de port à son entrée et à sa sortie, sauf si les connexions de masse sont choisies pour que cela se produise. Par exemple, du côté de l’entrée, le courant entrant dans l’amplificateur principal est IS. Ce courant est réparti de trois façons : vers le réseau de rétroaction, vers la résistance de polarisation RB et vers la résistance de base du transistor d’entrée rπ. Pour satisfaire la condition de port de l’amplificateur principal, les trois composants doivent être renvoyés du côté de l’entrée de l’amplificateur principal, ce qui signifie que tous les fils de masse étiquetés G1 doivent être connectés, ainsi que le fil d’émetteur GE1. De même, du côté sortie, toutes les connexions de masse G2 doivent être connectées, ainsi que la connexion de masse GE2. Ensuite, en bas du schéma, sous la rétroaction à deux ports et à l’extérieur des blocs amplificateurs, G1 est connecté à G2. Cela oblige les courants de masse à se diviser entre les côtés entrée et sortie comme prévu. Remarquez que cette disposition de connexion divise l’émetteur du transistor d’entrée en un côté base et un côté collecteur – une chose physiquement impossible à faire, mais électriquement le circuit voit toutes les connexions de masse comme un seul nœud, donc cette fiction est autorisée.
Bien sûr, la façon dont les fils de masse sont connectés ne fait aucune différence pour l’amplificateur (ils sont tous un seul nœud), mais elle fait une différence pour les conditions de port. Cette artificialité est une faiblesse de cette approche : les conditions de port sont nécessaires pour justifier la méthode, mais le circuit n’est vraiment pas affecté par la façon dont les courants sont échangés entre les connexions de masse.
Cependant, si aucun arrangement possible des conditions de masse ne conduit aux conditions de port, le circuit pourrait ne pas se comporter de la même façon. Les facteurs d’amélioration (1 + βFB AOL) pour déterminer l’impédance d’entrée et de sortie pourraient ne pas fonctionner. Cette situation est délicate, car l’impossibilité de réaliser un circuit à deux ports peut refléter un problème réel (ce n’est tout simplement pas possible) ou un manque d’imagination (par exemple, on n’a tout simplement pas pensé à diviser le nœud émetteur en deux). En conséquence, lorsque les conditions de port sont en doute, au moins deux approches sont possibles pour établir si les facteurs d’amélioration sont précis : soit simuler un exemple en utilisant Spice et comparer les résultats avec l’utilisation d’un facteur d’amélioration, soit calculer l’impédance en utilisant une source de test et comparer les résultats.
Un choix plus pratique est d’abandonner complètement l’approche à deux ports, et d’utiliser diverses alternatives basées sur la théorie des graphes de flux de signaux, y compris la méthode Rosenstark, la méthode Choma, et l’utilisation du théorème de Blackman. Ce choix peut être conseillé si les modèles de dispositifs à petits signaux sont complexes ou ne sont pas disponibles (par exemple, les dispositifs ne sont connus que numériquement, peut-être à partir de mesures ou de simulations SPICE).