#InsideRL

Tyypillisessä Reinforcement Learning (RL) -ongelmassa on oppija ja päätöksentekijä, jota kutsutaan agentiksi ja ympäristöä, jonka kanssa se on vuorovaikutuksessa, kutsutaan ympäristöksi. Ympäristö puolestaan tarjoaa palkintoja ja uuden tilan agentin toimien perusteella. Vahvistusoppimisessa emme siis opeta agentille, miten sen pitäisi tehdä jotakin, vaan annamme sille sen toimien perusteella joko positiivisia tai negatiivisia palkkioita. Tämän blogin peruskysymys on siis se, miten RL-ongelmat muotoillaan matemaattisesti. Tässä kohtaa Markovin päätösprosessi(MDP) astuu kuvaan.

Ennen kuin vastaamme perimmäiseen kysymykseen eli. Miten muotoilemme RL-ongelmat matemaattisesti (käyttäen MDP:tä), meidän on kehitettävä intuitiomme :

• Agentti-ympäristö-suhde
• Markovin ominaisuus
• Markovin prosessi ja Markovin ketjut
• Markovin palkitsemisprosessi (MRP)
• Bellmanin yhtälö
• Markovin palkitsemisprosessi

Naapikaa kahvinne älkääkä pysähtykö, ennen kuin olette ylpeitä!🧐

Agentti-ympäristö-suhde

Katsotaan ensin muutamia muodollisia määritelmiä :

Agentti : Ohjelmisto-ohjelmat, jotka tekevät älykkäitä päätöksiä ja ne ovat RL:n oppijoita. Nämä agentit ovat vuorovaikutuksessa ympäristön kanssa toimimalla ja saavat palkkioita toimiensa perusteella.

Ympäristö :Se on ratkaistavan ongelman esittely.Nyt meillä voi olla reaalimaailman ympäristö tai simuloitu ympäristö, jonka kanssa agenttimme on vuorovaikutuksessa.

Tila : Tämä on agenttien sijainti tietyllä aika-askeleella ympäristössä.siis,aina kun agentti suorittaa toiminnon,ympäristö antaa agentille palkkion ja uuden tilan,johon agentti saavutti suorittamalla toiminnon.

Kaikkea,mitä agentti ei voi muuttaa mielivaltaisesti,pidetään osana ympäristöä. Yksinkertaistettuna toiminta voi olla mikä tahansa päätös, jonka haluamme agentin oppivan, ja tila voi olla mikä tahansa, josta voi olla hyötyä toiminnan valinnassa. Emme oleta, että kaikki ympäristössä oleva on agentille tuntematonta, esimerkiksi palkkion laskemista pidetään ympäristön osana, vaikka agentti tietäisikin jonkin verran siitä, miten sen palkkio lasketaan sen toimien ja tilojen funktiona, joissa niitä tehdään. Tämä johtuu siitä, että agentti ei voi muuttaa palkkioita mielivaltaisesti. Joskus agentti saattaa olla täysin tietoinen ympäristöstään, mutta hänen on silti vaikea maksimoida palkkiotaan, kuten esimerkiksi tiedämme, miten Rubikin kuutiota pelataan, mutta emme silti osaa ratkaista sitä. Voimme siis turvallisesti sanoa, että agentti-ympäristö-suhde edustaa agentin hallinnan rajaa eikä sen tietämystä.

Markovin ominaisuus

Transition : Siirtymistä tilasta toiseen kutsutaan siirtymäksi.

Transition todennäköisyys: Todennäköisyyttä, että agentti siirtyy tilasta toiseen, kutsutaan siirtymätodennäköisyydeksi.

Markovin ominaisuuden mukaan :

”Tulevaisuus on riippumaton menneisyydestä, kun otetaan huomioon nykyisyys”

Matemaattisesti voimme ilmaista tämän väitteen seuraavasti :

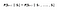
S tarkoittaa agentin nykyistä tilaa ja s tarkoittaa seuraavaa tilaa. Tämä yhtälö tarkoittaa sitä, että siirtyminen tilasta S tilaan S on täysin riippumaton menneisyydestä. Yhtälön RHS tarkoittaa siis samaa kuin LHS, jos järjestelmällä on Markovin ominaisuus. Intuitiivisesti se tarkoittaa sitä, että nykyinen tilamme sisältää jo tietoa menneistä tiloista.

Tilan siirtymätodennäköisyys :

Koska nyt tiedämme siirtymätodennäköisyydestä, voimme määritellä tilan siirtymätodennäköisyyden seuraavasti :

Markovin tilalle S:stä S:ään ts. mihin tahansa toiseen seuraajatilaan , tilan siirtymätodennäköisyys saadaan

Voidaan muotoilla tilan siirtymätodennäköisyys tilan siirtymätodennäköisyystodennäköisyystodennäköisyystodennäköisyystodennäköisyystodennäköisyystodennäköisyystodennäköisyystodennäköisyystodennäköisyysmatriisiksi :

Matriisin jokainen rivi edustaa todennäköisyyttä siirtyä alkuperäisestä tai alkutilastamme mihin tahansa seuraajatilaan.Jokaisen rivin summa on yhtä suuri kuin 1.

Markovin prosessi tai Markovin ketjut

Markovin prosessi on muistia vailla oleva satunnaisprosessi eli satunnaisten tilojen S,S,….S sekvenssi, jolla on Markovin ominaisuus.Kyseessä on siis pohjimmiltaan tilojen sekvenssi, jolla on Markovin ominaisuus.Se voidaan määritellä tilojen joukon(S) ja siirtymätodennäköisyystodennäköisyysmatriisin (P) avulla.Ympäristön dynamiikka voidaan täysin määritellä käyttämällä tiloja(S) ja siirtymätodennäköisyysmatriisia(P).

Mutta mitä satunnaisprosessi tarkoittaa ?

Kysymykseen vastaamiseksi tarkastellaan esimerkkiä:

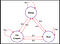
Puun särmät merkitsevät siirtymätodennäköisyyttä. Otetaan tästä ketjusta jokin otos. Oletetaan nyt, että olimme nukkumassa ja todennäköisyysjakauman mukaan on 0,6 mahdollisuus, että juoksemme ja 0,2 mahdollisuus, että nukumme enemmän ja taas 0,2, että syömme jäätelöä. Vastaavasti voimme ajatella muitakin sekvenssejä, joista voimme ottaa näytteitä tästä ketjusta.

Joitakin näytteitä ketjusta :

• Nukkuminen – Juokseminen – Jäätelö – Nukkuminen
• Nukkuminen – Jäätelö – Jäätelö – Jäätelö – Juokseminen

Yllä olevissa kahdessa sekvenssissä näemme, että saamme sattumanvaraisen joukon olotiloja(S)(eli Nukkuminen,Jäätelö,Nukkuminen ) joka kerta, kun juoksemme ketjun.Toivottavasti nyt on selvää, miksi Markov-prosessia kutsutaan satunnaisjoukoksi sekvensseistä.

Katsotaanpa ennen Markov-palkkio-prosessin käsittelyä muutamia tärkeitä käsitteitä, jotka auttavat meitä ymmärtämään MRP:tä.

Palkkio ja palautus

Palkkiot ovat numeerisia arvoja, joita agentti saa suorittaessaan jonkin toiminnon jossakin (jossakin) tilassa (jossakin) ympäristössä. Numeroarvo voi olla positiivinen tai negatiivinen agentin toimien perusteella.

Vahvistusoppimisessa huolehdimme kumulatiivisen palkkion maksimoimisesta (kaikki palkkiot, jotka agentti saa ympäristöstä) sen sijaan, että maksimoimme palkinnon, jonka agentti saa senhetkisestä tilasta (jota kutsutaan myös välittömäksi palkkioksi). Tätä agentin ympäristöstä saaman palkkion kokonaissummaa kutsutaan tuotoksi.

Voidaan määritellä Returns seuraavasti :

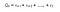
r on palkkio, jonka agentti saa aika-askeleella t suorittaessaan toiminnon(a) siirtyäkseen tilasta toiseen. Vastaavasti r on palkkio, jonka agentti saa aika-askeleella t suorittaessaan toiminnon siirtyäkseen toiseen tilaan. Ja r on palkkio, jonka agentti saa viimeisellä aika-askeleella suorittamalla toiminnon siirtyäkseen toiseen tilaan.

Episodiset ja jatkuvat tehtävät

Episodiset tehtävät: Nämä ovat tehtäviä, joilla on lopputila (lopputila).Voidaan sanoa, että niillä on äärelliset tilat. Esimerkiksi ajopeleissä aloitamme pelin (start the race) ja pelaamme sitä, kunnes peli on ohi (race ends!). Tätä kutsutaan episodiksi. Kun käynnistämme pelin uudelleen, se alkaa alkutilasta ja näin ollen jokainen jakso on itsenäinen.

Jatkuvat tehtävät : Nämä ovat tehtäviä, joilla ei ole loppua eli niillä ei ole lopputilaa. tämäntyyppiset tehtävät eivät koskaan lopu. esimerkiksi koodaamisen opettelu!

Nyt on helppo laskea episoditehtävien tuotot, koska ne loppuvat lopulta, mutta entä jatkuvat tehtävät, koska ne jatkuvat ikuisesti. Tuottojen summa on ääretön! Miten siis määrittelemme jatkuvien tehtävien tuoton?

Tässä kohtaa tarvitsemme Alennuskerrointa (ɤ).

Alennuskerroin (ɤ): Se määrittää, kuinka suuri merkitys annetaan välittömälle palkkiolle ja tuleville palkkioille. Tämä auttaa periaatteessa välttämään äärettömyyttä palkkiona jatkuvissa tehtävissä. Sen arvo on välillä 0 ja 1. Arvo 0 tarkoittaa, että välittömälle palkinnolle annetaan suurempi merkitys, ja arvo 1 tarkoittaa, että tuleville palkkioille annetaan suurempi merkitys. Käytännössä diskonttauskerroin, jonka arvo on 0, ei koskaan opi, koska se ottaa huomioon vain välittömän palkkion, ja diskonttauskerroin, jonka arvo on 1, ottaa huomioon tulevat palkkiot, mikä voi johtaa äärettömyyteen. Siksi diskonttauskertoimen optimaalinen arvo on välillä 0,2-0,8.

Voidaan siis määritellä tuotot diskonttauskertoimen avulla seuraavasti :(Sanotaan, että tämä on yhtälö 1 ,koska käytämme tätä yhtälöä myöhemmin Bellmanin yhtälön johtamiseen)

Ymmärretään se esimerkin avulla,Oletetaan, että asut paikassa, jossa sinulla on vesipula, joten jos joku tulee luoksesi ja sanoo, että hän antaa sinulle 100 litraa vettä!(olettakaa kiitos!) seuraavien 15 tunnin aikana jonkin parametrin (ɤ) funktiona.Tarkastellaan kahta vaihtoehtoa : (Sanotaan, että tämä on yhtälö 1 ,koska käytämme tätä yhtälöä myöhemmin Bellmanin yhtälön johtamiseen)

Yksi, jossa diskonttokerroin (ɤ) on 0.8 :

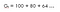
Tämä tarkoittaa, että kannattaa odottaa 15. tuntiin asti, koska lasku ei ole kovin merkittävä , joten kannattaa silti mennä loppuun asti.tämä tarkoittaa, että olemme kiinnostuneita myös tulevista palkkioista.Joten jos diskonttauskerroin on lähellä 1, niin pyrimme menemään loppuun asti, koska palkkiot ovat merkittäviä.

Toiseksi, diskonttauskertoimen (ɤ) ollessa 0.2 :

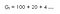
Tämä tarkoittaa, että olemme kiinnostuneempia varhaisista palkkioista, koska palkkiot pienenevät huomattavasti tunnissa.Emme siis välttämättä halua odottaa loppuun asti (15. tuntiin asti), koska se on arvotonta.Jos siis diskonttauskerroin on lähellä nollaa, välittömät palkkiot ovat tärkeämpiä kuin tulevat.

Minkä arvoista diskonttauskerrointa käytetään?

Se riippuu tehtävästä, jota varten haluaisimme kouluttaa agentin. Oletetaan, että shakkipelissä tavoitteena on voittaa vastustajan kuningas. Jos annamme painoarvoa välittömille palkkioille, kuten palkkiolle, kun sotilas voittaa minkä tahansa vastustajan pelaajan, agentti oppii suorittamaan nämä osatavoitteet riippumatta siitä, voitetaanko myös hänen pelaajansa. Tässä tehtävässä tulevat palkkiot ovat siis tärkeämpiä. Joissakin tapauksissa saatamme käyttää mieluummin välittömiä palkkioita, kuten aiemmin näkemässämme vesiesimerkissä.

Markovin palkitsemisprosessi

Tähän asti olemme nähneet, miten Markovin ketju määrittelee ympäristön dynamiikan käyttämällä tilojen joukkoa (S) ja siirtymätodennäköisyysmatriisia (P).Tiedämme kuitenkin, että vahvistusoppimisessa on kyse tavoitteesta maksimoida palkkio.Lisäämme siis palkinnon Markovin ketjuun.Näin saamme Markovin palkitsemisprosessin.

Markovin palkitsemisprosessi : Kuten nimestä voi päätellä, MDP:t ovat Markovin ketjuja, joissa on arvojen arviointi.Periaatteessa saamme arvon jokaisesta tilasta, jossa agenttimme on.

Matemaattisesti määrittelemme Markovin palkitsemisprosessin seuraavasti :

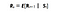
Mitä tämä yhtälö tarkoittaa, on se, kuinka paljon palkkiota (Rs) saamme jostain tietystä tilasta S. Tämä kertoo välittömän palkkiomme siitä tietystä tilasta, jossa agenttimme on. Kuten näemme seuraavassa tarinassa, miten maksimoimme nämä palkkiot jokaisesta tilasta, jossa agenttimme on. Yksinkertaisesti sanottuna maksimoimme kumulatiivisen palkkion, jonka saamme kustakin tilasta.

Määrittelemme MRP:n seuraavasti: (S,P,R,ɤ) ,missä :

• S on joukko tiloja,
• P on siirtymätodennäköisyysmatriisi,
• R on palkitsemisfunktio , jonka näimme aiemmin,
• ɤ on diskonttauskerroin

Markovin päätöksentekoprosessi

Kehitellään nyt intuitiotamme Bellmanin yhtälöä ja Markovin päätöksentekoprosessia varten.

Policy Function ja Value Function

Valuefunktio määrittää, kuinka hyvä agentin on olla tietyssä tilassa. Tietysti sen määrittämiseksi, kuinka hyvä on olla tietyssä tilassa, sen täytyy riippua joistakin toimista, joita se tekee. Tässä kohtaa politiikka tulee kuvaan mukaan. Politiikka määrittelee, mitä toimia suoritetaan tietyssä tilassa s.

Politiikka on yksinkertainen funktio, joka määrittelee todennäköisyysjakauman toimille (a∈ A) jokaiselle tilalle (s ∈ S). Jos agentti ajanhetkellä t noudattaa politiikkaa π, π(a|s) on todennäköisyys, että agentti ryhtyy toimeen (a ) tietyllä aika-askeleella (t).Vahvistavassa oppimisessa agentin kokemus määrittää politiikan muutoksen. Matemaattisesti politiikka määritellään seuraavasti :

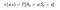
Nyt, miten löydämme tilan arvon.Tilan s arvo, kun agentti noudattaa politiikkaa π, jota merkitään vπ(s), on odotettu tuotto alkaen tilasta s ja seuraten politiikkaa π seuraavissa tiloissa,kunnes saavutamme lopputilan.Voimme muotoilla tämän seuraavasti :(Tätä funktiota kutsutaan myös tila-arvofunktioksi)

Tämän yhtälön avulla saamme odotetun tuoton, joka alkaa tilasta(s) ja kulkee sen jälkeen seuraaviin seuraajina oleviin tiloihin, joissa noudatetaan politiikkaa π. On huomattava, että saamamme tuotot ovat stokastisia, kun taas tilan arvo ei ole stokastinen. Se on tuotto-odotus alkutilasta s ja sen jälkeen mistä tahansa muusta tilasta. Huomaa myös, että lopputilan arvo (jos sellainen on olemassa) on nolla. Tarkastellaan esimerkkiä :

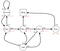
Esitettäköön, että alkutilamme on luokka 2 ja siirrymme luokkaan 3, sitten luokkaan Pass ja sen jälkeen luokkaan Sleep. lyhyesti sanottuna: Luokka 2 > Luokka 3 > Pass > Sleep.

Odotettu tuottomme on diskonttauskertoimella 0,5:

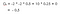
Huomautus: Se on -2 + (-2 * 0.5) + 10 * 0.25 + 0 eikä -2 * -2 * 0.5 + 10 * 0.25 + 0.Silloin luokan 2 arvo on -0.5 .

Bellmanin yhtälö arvofunktiolle

Bellmanin yhtälö auttaa meitä löytämään optimaaliset politiikat ja arvofunktion.Tiedämme, että politiikkamme muuttuu kokemuksen myötä, joten meillä on erilainen arvofunktio eri politiikoille.Optimaalinen arvofunktio on sellainen, joka antaa maksimaalisen arvon verrattuna kaikkiin muihin arvofunktioihin.

Bellmanin yhtälön mukaan arvofunktio voidaan purkaa kahteen osaan:

• välitön palkkio, R
• seuraavien tilojen diskontattu arvo,

Matemaattisesti voimme määritellä Bellmanin yhtälön seuraavasti :

Ymmärretäänpä esimerkin avulla, mitä tämä yhtälö sanoo :

Esitettäköön, että robotti on jossakin tilassa (s) ja sitten hän siirtyy tästä tilasta johonkin toiseen tilaan (s’). Nyt kysytään, kuinka hyvä robotin oli olla tilassa(s). Bellmanin yhtälön avulla voimme todeta, että se on odotusarvo palkkiosta, jonka se sai poistuessaan tilasta (s), lisättynä sen tilan (s’) arvolla, johon se siirtyi.

Katsotaan toinen esimerkki :

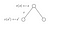
Haluamme tietää tilan s arvon.Tilan s arvo on palkkio, jonka saimme poistuessamme kyseisestä tilasta, plus sen tilan diskontattu arvo, johon laskeuduimme, kerrottuna siirtymätodennäköisyydellä, että siirrymme siihen.

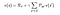
Yllä oleva yhtälö voidaan ilmaista matriisimuodossa seuraavasti :

Jossa v on sen tilan arvo, jossa olimme, joka on yhtä suuri kuin välitön palkkio lisättynä seuraavan tilan diskontatulla arvolla kerrottuna todennäköisyydellä siirtyä tähän tilaan.

Tämän laskutoimituksen ajallinen monimutkaisuus on O(n³). Siksi tämä ei selvästikään ole käytännöllinen ratkaisu suurempien MRP:iden ratkaisemiseen (sama koskee myös MDP:tä).Myöhemmissä blogeissa tarkastelemme tehokkaampia menetelmiä, kuten dynaamista ohjelmointia (arvo-iteraatio ja politiikka-iteraatio), Monte-Claro-menetelmiä ja TD-oppimista.

Keskustelemme Bellmanin yhtälöstä paljon yksityiskohtaisemmin seuraavassa jutussa.

Mikä on Markovin päätöksentekoprosessi?

Markovin päätöksentekoprosessi : Se on Markovin palkitsemisprosessi, jossa on päätöksiä.Kaikki on samaa kuin MRP:ssä, mutta nyt meillä on varsinainen virasto, joka tekee päätöksiä tai ryhtyy toimiin.

Se on tupli (S, A, P, R, 𝛾), jossa:

• S on joukko tiloja,
• A on joukko toimia, jotka agentti voi valita tekevänsä,
• P on siirtymätodennäköisyystodennäköisyysmatriisi,
• R on agentin toimista kertynyt palkinto,
• 𝛾 on diskonttokerroin.

P ja R muuttuvat hieman toimien suhteen seuraavasti :

Transition Probability Matrix

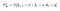
Palkkiofunktio

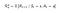
Nyt palkitsemisfunktiomme on riippuvainen actionista.

Tähän asti olemme puhuneet siitä, että saamme palkkion (r), kun agenttimme käy läpi joukon tiloja (s) noudattaen politiikkaa π.Itse asiassa Markovin päätöksentekoprosessissa (MDP) politiikka on mekanismi, jolla tehdään päätöksiä.Nyt meillä on siis mekanismi, joka valitsee toimen.

Politiikat MDP:ssä riippuvat nykyisestä tilasta.Ne eivät riipu historiasta.Se on Markovin ominaisuus.Nykyinen tila, jossa olemme, luonnehtii siis historiaa.

Olemme jo nähneet, kuinka hyvä agentin on olla tietyssä tilassa(Tila-arvofunktio).Katsotaan nyt, kuinka hyvä on tehdä tietty toiminta politiikkaa π noudattaen tilasta s (Toiminta-arvofunktio).

Tila-toiminta-arvofunktio tai Q-funktio

Tämä funktio määrittelee, kuinka hyvä agentin on tehdä toiminta (a) tilassa (s) politiikalla π.

Matemaattisesti voimme määritellä State-action value function seuraavasti :

Periaatteessa se kertoo, kuinka arvokasta on suorittaa tietty toiminto (a) tilassa (s) politiikalla π.

Katsotaanpa esimerkki Markovin päätösprosessista :

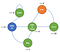
Nyt näemme, että todennäköisyyksiä ei enää ole.Itse asiassa nyt agentillamme on valinnanvaraa, kuten heräämisen jälkeen voimme valita katsommeko Netflixiä vai koodaammeko ja debuggaammeko.Tietenkin agentin toimet on määritelty jonkin politiikan π mukaan ja saamme palkkion sen mukaisesti.