
Vaikka, kuten kohdassa Signaalivirta-analyysi mainittiin, jonkinlainen signaalivirta-analyysi on yleisin tapa käsitellä negatiivisen takaisinkytkennän vahvistinta, esitystapa kahtena kaksiporttisena on oppikirjoissa useimmiten esitetty lähestymistapa, ja se esitetään tässä. Siinä säilytetään vahvistimen kahden lohkon piirijako, mutta lohkot voivat olla kahdenvälisiä. Joitakin tämän menetelmän haittoja kuvataan lopussa.
Elektroniset vahvistimet käyttävät tulona ja lähtönä virtaa tai jännitettä, joten neljä vahvistintyyppiä on mahdollista (mikä tahansa kahdesta mahdollisesta sisääntulosta millä tahansa kahdesta mahdollisesta ulostulosta). Katso vahvistimien luokittelu. Takaisinkytkentävahvistimen tavoite voi olla mikä tahansa näistä neljästä vahvistintyypistä, eikä se välttämättä ole samaa tyyppiä kuin avoimen silmukan vahvistin, joka itsessään voi olla mikä tahansa näistä tyypeistä. Niinpä esimerkiksi op-vahvistin (jännitevahvistin) voidaan järjestää niin, että sen sijaan saadaan aikaan virtavahvistin.
Minkä tahansa tyyppiset negatiivisen takaisinkytkennän vahvistimet voidaan toteuttaa käyttämällä kahden portin verkkojen yhdistelmiä. Kaksiporttisia verkkoja on neljää eri tyyppiä, ja halutun vahvistimen tyyppi sanelee kaksiporttisten verkkojen valinnan ja yhden neljästä eri kytkentätopologiasta, jotka on esitetty kuvassa. Näihin kytkentöihin viitataan yleensä sarja- tai shunttikytkentöinä (rinnakkaiskytkentöinä). Kaaviossa vasemmassa sarakkeessa on shunttitulot ja oikeassa sarakkeessa sarjatulot. Ylärivillä on sarjalähdöt ja alarivillä shunttilähdöt. Seuraavassa taulukossa on lueteltu eri kytkentäyhdistelmät ja kaksiporttiset liitännät.
| Takaisinkytkentävahvistimen tyyppi | Tuloliitäntä | Lähtöliitäntä | Ideaalinen takaisinkytkentä | Kaksoiskytkentä | Kaksi-portin takaisinkytkentä |
|---|---|---|---|---|---|
| Virta | Shuntti | Sarja | CCCS | g-parametri | |
| Transresistanssi | Shuntti | Shuntti | CCVS | y-parametri | |
| Transkonduktanssi | Sarja | Sarja | VCCS | z-parametri | |
| Jännite | Sarja | Shuntti | VCVS | h-parametri |
Esim, virran takaisinkytkentävahvistimessa ulostulon virta otetaan näytteeksi takaisinkytkentää varten ja yhdistetään tulossa olevaan virtaan. Siksi takaisinkytkentä suoritetaan ideaalisesti käyttämällä (ulostulon) virtaohjattua virtalähdettä (CCCS), ja sen epätäydellisen toteutuksen, jossa käytetään kaksiporttista verkkoa, on myös sisällettävä CCCS, eli sopiva valinta takaisinkytkentäverkoksi on g-parametrinen kaksiporttinen. Tässä esitellään useimmissa oppikirjoissa käytetty kaksiporttinen menetelmä käyttäen asymptoottista vahvistusmallia käsittelevässä artikkelissa käsiteltyä piiriä.

Kuvassa 3 on esitetty kahden transistorin vahvistin, jossa on takaisinkytkentävastus Rf. Tarkoituksena on analysoida tätä piiriä ja löytää kolme asiaa: vahvistus, vahvistimeen kuormasta katsottuna lähtöimpedanssi ja vahvistimeen lähteestä katsottuna tuloimpedanssi.
- Takaisinkytkentäverkon korvaaminen kaksiporttisellaEdit
- Piensignaalipiiri Muokkaa
- Kuormitettu avoimen silmukan vahvistusMuokkaa
- Vahvistus takaisinkytkennälläEdit
- Sisääntulo- ja ulostuloresistanssitEdit
- Taustaa resistanssin määrittämisestäEdit
- Soveltaminen esimerkkivahvistimeenMuokkaa
- Kuormitusjännite ja kuormitusvirtaEdit
- Onko päävahvistinlohko kaksiporttinen?Edit
Takaisinkytkentäverkon korvaaminen kaksiporttisellaEdit
Ensimmäinen vaihe on takaisinkytkentäverkon korvaaminen kaksiporttisella. Mitä komponentteja juuri kaksiporttiseen menee?
Kaksiporttisen tulopuolella meillä on Rf. Jos jännite Rf:n oikealla puolella muuttuu, se muuttaa Rf:ssä olevaa virtaa, joka vähennetään tulotransistorin pohjaan tulevasta virrasta. Toisin sanoen kaksiportin tulopuoli on riippuvainen virtalähde, jota ohjaa vastuksen R2 yläpuolella oleva jännite.
Voidaan sanoa, että vahvistimen toinen vaihe on vain jännitteen seuraaja, joka välittää jännitteen tulotransistorin kollektorissa R2:n yläpuolelle. Toisin sanoen valvottu lähtösignaali on todella jännite tulotransistorin kollektorissa. Tämä näkemys on oikeutettu, mutta silloin jänniteseurantavaiheesta tulee osa takaisinkytkentäverkkoa. Tämä tekee takaisinkytkennän analysoinnista monimutkaisempaa.
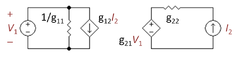
Vaihtoehtoinen näkemys on, että jännite R2:n yläpäässä määräytyy lähtötransistorin emitterivirran mukaan. Tämä näkemys johtaa täysin passiiviseen takaisinkytkentäverkkoon, joka koostuu R2:sta ja Rf:stä. Takaisinkytkentää ohjaava muuttuja on emitterivirta, joten takaisinkytkentä on virtaohjattu virtalähde (CCCS). Käymme läpi neljä saatavilla olevaa kaksiporttista verkkoa ja huomaamme, että ainoa CCCS:n sisältävä verkko on kuvassa 4 esitetty g-parametrinen kaksiporttinen verkko. Seuraavana tehtävänä on valita g-parametrit siten, että kuvan 4 kaksiporttinen verkko vastaa sähköisesti R2:n ja Rf:n muodostamaa L-jaksoa. Tämä valinta on algebrallinen menettely, joka tehdään yksinkertaisimmin tarkastelemalla kahta yksittäistä tapausta: tapaus, jossa V1 = 0, jolloin kaksoisportin oikeanpuoleinen VCVS on oikosulku, ja tapaus, jossa I2 = 0, jolloin vasemmanpuoleinen CCCS on avoin piiri. Algebra näissä kahdessa tapauksessa on yksinkertaista, paljon helpompaa kuin kaikkien muuttujien ratkaiseminen kerralla. Seuraavassa taulukossa esitetään g-parametrien valinta, joka saa kaksiportin ja L-osan käyttäytymään samalla tavalla.
| g11 | g12 | g21 | g22 |
|---|---|---|---|
1 R f + R 2 {\displaystyle {\frac {1}{R_{{\mathrm {f} }+R_{2}}}}
 |
– R 2 R 2 + R f {\displaystyle -{\frac {R_{2}}{R_{2}+R_{\mathrm {f} }}}}
 |
R 2 R 2 + R f {\displaystyle {\frac {\frac {R_{2}}{R_{2}+R_{\mathrm {f} }}}}
 |
R 2 / / R f {\displaystyle R_{2}//R_{\mathrm {f} }\ }
 |
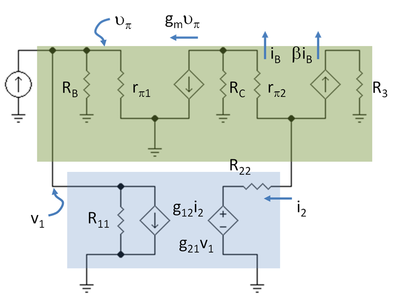
Piensignaalipiiri Muokkaa
Seuraavaksi piirretään piensignaalikaavio vahvistimelle, jossa kaksiportti on paikallaan, käyttäen transistorien hybridi-pi-mallia. Kuvassa 5 on esitetty kaavio merkinnöillä R3 = RC2 // RL ja R11 = 1 / g11, R22 = g22.
Kuormitettu avoimen silmukan vahvistusMuokkaa
Kuvassa 3 on ilmoitettu lähtösolmu, mutta ei lähtömuuttujan valintaa. Hyödyllinen valinta on vahvistimen oikosulkuvirtalähtö (johtaa oikosulkuvirran vahvistukseen). Koska tämä muuttuja johtaa yksinkertaisesti mihin tahansa muuhun valintaan (esimerkiksi kuormitusjännite tai kuormitusvirta), oikosulkuvirran vahvistus etsitään jäljempänä.
Ensin etsitään kuormitetun avoimen silmukan vahvistus. Takaisinkytkentä kytketään pois päältä asettamalla g12 = g21 = 0. Ajatuksena on löytää, kuinka paljon vahvistimen vahvistus muuttuu takaisinkytkentäverkossa olevien vastusten takia yksinään, kun takaisinkytkentä on pois päältä. Tämä laskenta on melko helppoa, koska R11, RB ja rπ1 ovat kaikki rinnakkain ja v1 = vπ. Olkoon R1 = R11 // RB // rπ1. Lisäksi i2 = -(β+1) iB. Tulos avoimen silmukan virtavahvistukselle AOL on:
A O L = β i B i S = g m R C ( β β β + 1 ) ( R 1 R 22 + r π 2 + R C β + 1 ) . {\displaystyle A_{\mathrm {OL} }={\frac {\beta i_{\mathrm {B} }}{i_{\mathrm {S}{i_mathrm {S}{i_mathrm {S} }}}=g_{m}R_{{\mathrm {C}} }\left({\frac {\beta }{\beta +1}}\right)\left({\frac {R_{1}}{R_{22}+{\frac {r_{\pi 2}+R_{\mathrm {C}}} }}{\beta +1}}}}\right)\ .} .}

Vahvistus takaisinkytkennälläEdit
Klassisessa takaisinkytkennässä VCVS:n edustama feedforward (eli g21 v1) jätetään huomiotta. Tämä saa kuvan 5 piirin muistuttamaan kuvan 1 lohkokaaviota, ja vahvistus takaisinkytkennän kanssa on tällöin:
A F B = A O L 1 + β F B A O L {\displaystyle A_{\mathrm {FB} }={\frac {A_{\mathrm {OL}} }}{1+{\beta}_{\mathrm {FB} }A_{\mathrm {OL} }}}}

A F B = A O L 1 + R 2 R 2 + R f A O L , {\displaystyle A_{\mathrm {FB} }={\frac {A_{\mathrm {OL} }}{1+{\frac {R_{2}}{R_{2}+R_{{\mathrm {f}} }}}A_{\mathrm {OL}}A_{\mathrm {OL}}A_{\mathrm {OL} }}}\\ ,}

jossa takaisinkytkentäkerroin βFB = -g12. Takaisinkytkentäkertoimelle on otettu käyttöön merkintä βFB, jotta se voidaan erottaa transistorin β:stä.
Sisääntulo- ja ulostuloresistanssitEdit

Takaisinkytkentää käytetään signaalilähteiden ja niiden kuormien parempaan sovittamiseen. Esimerkiksi jännitelähteen suora kytkentä resistiiviseen kuormaan voi johtaa signaalin häviämiseen jännitteen jakautumisen vuoksi, mutta negatiivisen takaisinkytkentävahvistimen välikytkentä voi kasvattaa lähteen näkemää näennäistä kuormaa ja pienentää kuorman näkemää näennäistä kuljettajan impedanssia, jolloin vältetään jännitteen jakautumisen aiheuttama signaalin vaimeneminen. Tämä etu ei rajoitu vain jännitevahvistimiin, vaan analogisia parannuksia sovituksessa voidaan järjestää virtavahvistimille, transkonduktanssivahvistimille ja transresistanssivahvistimille.
Tämän takaisinkytkennän vaikutuksen selittämiseksi impedansseihin tarvitaan ensin ekskursio siitä, miten kaksiporttiteoriassa lähestytään resistanssin määrittämistä, ja sen jälkeen sen soveltaminen käsillä olevaan vahvistimeen.
Taustaa resistanssin määrittämisestäEdit
Kuvassa 6 on esitetty ekvivalenttipiiri takaisinkytketyn jännitevahvistimen (vasemmalla) ja takaisinkytketyn virtavahvistimen (oikealla) sisääntuloresistanssin löytämiseksi. Nämä järjestelyt ovat tyypillisiä Millerin teoreeman sovelluksia.
Jännitevahvistimen tapauksessa takaisinkytkentäverkon lähtöjännite βVout kytketään sarjaan ja vastakkaisella polariteetilla kuin silmukan yli kulkeva tulojännite Vx (mutta maan suhteen polariteetit ovat samat). Tämän seurauksena tehollinen jännite vahvistimen sisääntulovastuksen Rin yli ja virta vahvistimen sisääntulovastuksen Rin läpi pienenevät niin, että piirin sisääntulovastus kasvaa (voisi sanoa, että Rin ilmeisesti kasvaa). Sen uusi arvo voidaan laskea soveltamalla Millerin teoreemaa (jännitteille) tai piirin peruslakeja. Siten Kirchhoffin jännitelaki antaa:
V x = I x R i n + β v o u t , {\displaystyle V_{x}=I_{x}R_{\mathrm {in} }+\beta v_{\mathrm {out} }\ ,}

jossa vout = Av vin = Av Ix Rin. Kun tämä tulos korvataan edellä olevaan yhtälöön ja ratkaistaan takaisinkytkentävahvistimen sisääntulovastuksen suhteen, saadaan tulos:
R i n ( f b ) = V x I x = ( 1 + β A v ) R i n . {\displaystyle R_{\mathrm {in} }(fb)={\frac {V_{x}}{I_{x}}}=\left(1+\beta A_{v}\right)R_{{\mathrm {in}} }\ .}

Yleinen johtopäätös tästä esimerkistä ja vastaavasta esimerkistä lähtövastuksen tapauksessa on: Sarjatakaisinkytkentä sisääntulossa (ulostulossa) kasvattaa sisääntulon (ulostulon) vastusta kertoimella ( 1 + β AOL ), missä AOL = avoimen silmukan vahvistus.
Virtavahvistimessa toisaalta takaisinkytkentäverkon ulostulon virtaa βIout syötetään samansuuntaisena ja vastakkaissuuntaisena sisääntulon tulovirralle Ix. Tämän seurauksena piirin sisääntulon kautta kulkeva kokonaisvirta (ei vain sisääntulovastuksen Rin kautta) kasvaa ja sen yli kulkeva jännite pienenee niin, että piirin sisääntulovastus pienenee (Rin ilmeisesti pienenee). Sen uusi arvo voidaan laskea soveltamalla kaksois-Millerin teoreemaa (virroille) tai Kirchhoffin peruslakeja:
I x = V i n R i n + β i o u t . {\displaystyle I_{x}={\frac {V_{\mathrm {in} }}{R_{\mathrm {in}{R_mathrm {in}{R_mathrm {in} }}}+\beta i_{\mathrm {out}}} }\ .}

jossa iout = Ai iin = Ai Vx / Rin. Kun tämä tulos korvataan edellä olevaan yhtälöön ja ratkaistaan takaisinkytkentävahvistimen sisääntulovastuksen suhteen, saadaan tulos:
R i n ( f b ) = V x I x = R i n ( 1 + β A i ) . {\displaystyle R_{\mathrm {in} }(fb)={\frac {V_{x}}{I_{x}}}={\frac {R_{\mathrm {in}}} }}{\left(1+\beta A_{i}\right)}\ .}\ .}

Yleinen johtopäätös tästä esimerkistä ja vastaavasta esimerkistä lähtövastuksen tapauksessa on: Rinnakkainen takaisinkytkentä sisääntulossa (ulostulossa) pienentää sisääntulon (ulostulon) resistanssia kertoimella ( 1 + β AOL ), missä AOL = avoimen silmukan vahvistus.
Nämä johtopäätökset voidaan yleistää käsittelemään tapauksia, joissa on mielivaltaisia Nortonin tai Théveninin asemia, mielivaltaisia kuormia ja yleisiä kahden portin takaisinkytkentäverkkoja. Tulokset riippuvat kuitenkin siitä, että päävahvistimen esitys on kaksiporttinen – toisin sanoen tulokset riippuvat siitä, että tuloterminaaleihin tulee ja niistä lähtee sama virta, ja vastaavasti saman virran, joka lähtee toisesta lähtöterminaalista, on tultava toiseen lähtöterminaaliin.
Kvantitatiivisista yksityiskohdista riippumaton laajempi johtopäätös on, että takaisinkytkentää voidaan käyttää tulo- ja lähtöimpedanssin kasvattamiseen tai pienentämiseen.
Soveltaminen esimerkkivahvistimeenMuokkaa
Näitä resistanssituloksia sovelletaan nyt kuvien 3 ja 5 vahvistimiin. Vahvistusta pienentävä parannuskerroin eli ( 1 + βFB AOL) ratkaisee suoraan takaisinkytkennän vaikutuksen vahvistimen tulo- ja lähtövastuksiin. Shunttikytkennän tapauksessa tuloimpedanssi pienenee tällä kertoimella, ja sarjakytkennän tapauksessa impedanssi kerrotaan tällä kertoimella. Takaisinkytkennän muuttama impedanssi on kuitenkin kuvan 5 vahvistimen impedanssi, kun takaisinkytkentä on kytketty pois päältä, ja se sisältää takaisinkytkentäverkon vastusten aiheuttamat muutokset impedanssiin.
Siten lähteen näkemä tuloimpedanssi, kun takaisinkytkentä on kytketty pois päältä, on Rin = R1 = R11 // RB // rπ1, ja kun takaisinkytkentä on kytketty päälle (mutta ei takaisinkytkentää)
R i n = R 1 1 + β F B A O L , {\displaystyle R_{{\mathrm {in} }={\frac {R_{1}}{1+{\beta }_{{\mathrm {FB}} }A_{\mathrm {OL} }}}\ ,}

jossa käytetään jakoa, koska tulokytkentä on shunttiliitäntä: takaisinkytketty kaksiporttinen takaisinkytkentä on rinnakkain signaalilähteen kanssa vahvistimen tulopuolella. Muistutus: AOL on edellä todettu kuormitetun avoimen silmukan vahvistus, jota on muokattu takaisinkytkentäverkon vastuksilla.
Kuorman näkemä impedanssi kaipaa lisää keskustelua. Kuvassa 5 esitetty kuorma on kytketty lähtötransistorin kollektoriin, ja siksi se on erotettu vahvistimen rungosta lähtövirtalähteen äärettömällä impedanssilla. Siksi takaisinkytkennällä ei ole mitään vaikutusta lähtöimpedanssiin, joka pysyy yksinkertaisesti RC2:na, kuten kuorman vastus RL näkee kuvassa 3.
Jos sen sijaan haluaisimme löytää impedanssin, joka esitetään lähtötransistorin emitterissä (sen kollektorin sijasta), joka on sarjaan kytketty takaisinkytkentäverkkoon, takaisinkytkentä lisäisi tätä vastusta parannuskertoimella ( 1 + βFB AOL).
Kuormitusjännite ja kuormitusvirtaEdit
Edellä johdettu vahvistus on virtavahvistus lähtötransistorin kollektorissa. Tämän vahvistuksen suhteuttamiseksi vahvistukseen, kun vahvistimen ulostulona on jännite, huomaa, että lähtöjännite kuormalla RL liittyy kollektorivirtaan Ohmin lain avulla seuraavasti: vL = iC (RC2 || RL). Näin ollen transresistanssivahvistus vL / iS saadaan kertomalla virtavahvistus RC2 || RL:llä:
v L i S = A F B ( R C 2 ∥ R L ) . {\displaystyle {\frac {v_{\mathrm {L} }}{i_{{\mathrm {S}}{i_mathrm {S}{i_mathrm {S}{i_mathrm {S} }}}=A__{\mathrm {FB}} }(R_{\mathrm {C2} }\paralleeli R_{\mathrm {L} })\ .}

Samoin jos vahvistimen ulostulo otetaan kuormitusvastuksen RL virraksi, virranjako määrittää kuormitusvirran, ja vahvistus on tällöin:
i L i S = A F B R C 2 R C 2 R C 2 + R L . {{\displaystyle {\frac {i_{\mathrm {L}} }}{i_{\mathrm {S} }}}=A__{\mathrm {FB}} {{\frac {R_{\mathrm {C2}} }}{R_{\mathrm {C2}}{R_\mathrm {C2}}{R_\mathrm {C2} }+R_{{\mathrm {L}} }}}\ .}

Onko päävahvistinlohko kaksiporttinen?Edit

Seuraavaksi seuraa tarkkaavaiselle lukijalle tarkoitettuja kahden kaksoporttisen lähestymistavan haittapuolia.
Kuvassa 7 on esitetty piensignaalikaavio, jossa päävahvistin ja takaisinkytketty kaksoporttinen ovat tummennetuissa laatikoissa. Takaisinkytketty kaksiporttinen täyttää porttiehdot: sisääntuloportissa porttiin tulee ja sieltä poistuu Iin, ja samoin ulostulossa porttiin tulee ja sieltä poistuu Iout.
Onko päävahvistimen lohko myös kaksiporttinen? Päävahvistin on esitetty ylemmässä tummennetussa laatikossa. Maaliitännät on merkitty. Kuvasta 7 nähdään se mielenkiintoinen seikka, että päävahvistin ei täytä porttiehtoja tulossaan ja lähdössään, ellei maadoitusliitäntöjä valita siten, että näin tapahtuu. Esimerkiksi tulopuolella päävahvistimeen tuleva virta on IS. Tämä virta jakautuu kolmeen suuntaan: takaisinkytkentäverkkoon, bias-vastukseen RB ja tulotransistorin perusresistanssiin rπ. Jotta päävahvistimen porttiehto täyttyisi, kaikki kolme komponenttia on palautettava päävahvistimen tulopuolelle, mikä tarkoittaa, että kaikki maadoitusjohdot, joissa on merkintä G1, on kytkettävä, samoin kuin emitterijohto GE1. Vastaavasti lähtöpuolella on kytkettävä kaikki maadoitusjohdot G2 ja myös maadoitusjohto GE2. Sitten kaavion alaosassa, takaisinkytkentäkaksoisportin alapuolella ja vahvistinlohkojen ulkopuolella, G1 on kytketty G2:een. Tämä pakottaa maasulkuvirrat jakautumaan tulo- ja lähtöpuolen välillä suunnitellulla tavalla. Huomaa, että tämä kytkentäjärjestely jakaa tulotransistorin emitterin pohja-puolelle ja kollektori-puolelle – fyysisesti mahdoton asia, mutta sähköisesti piiri näkee kaikki maadoitusliitännät yhtenä solmuna, joten tämä fiktio on sallittu.
Tapa, jolla maadoitusjohdot on kytketty, ei tietenkään muuta vahvistinta (ne ovat kaikki yhtä solmua), mutta porttiolosuhteisiin sillä on merkitystä. Tämä keinotekoisuus on tämän lähestymistavan heikkous: porttiolosuhteita tarvitaan menetelmän perustelemiseksi, mutta piiriin ei todellakaan vaikuta se, miten virrat käyvät kauppaa maadoitusliitäntöjen välillä.
Mutta jos mikään mahdollinen maadoitusolosuhteiden järjestely ei johda porttiolosuhteisiin, piiri ei välttämättä käyttäydy samalla tavalla. Parannuskertoimet (1 + βFB AOL) tulo- ja lähtöimpedanssin määrittämiseksi eivät välttämättä toimi. Tämä tilanne on hankala, koska epäonnistuminen kahden portin tekemisessä voi heijastaa todellista ongelmaa (se ei vain ole mahdollista) tai heijastaa mielikuvituksen puutetta (esimerkiksi ei vain ajatellut jakaa emitterisolmua kahtia). Tämän seurauksena, kun porttiolosuhteet ovat epävarmoja, on ainakin kaksi lähestymistapaa, joilla voidaan selvittää, ovatko parannuskertoimet tarkkoja: joko simuloidaan esimerkki Spicen avulla ja verrataan tuloksia parannuskertoimen käyttöön tai lasketaan impedanssi testilähteen avulla ja verrataan tuloksia.
Käytännöllisempi vaihtoehto on luopua kokonaan kaksiporttisesta lähestymistavasta ja käyttää erilaisia signaalivirtauksen kuvaajateoriaan pohjautuvia vaihtoehtoja, mukaan lukien Rosenstarkin menetelmää, Choma-menetelmää ja Blackmanin lauseen käyttöä. Tämä valinta voi olla suositeltava, jos pienisignaaliset laitemallit ovat monimutkaisia tai niitä ei ole saatavilla (esimerkiksi jos laitteet tunnetaan vain numeerisesti, ehkä mittauksista tai SPICE-simulaatioista).