Elektromagneettinen metamateriaali vaikuttaa sähkömagneettisiin aaltoihin, jotka osuvat sen aallonpituutta pienempiin rakenteellisiin ominaisuuksiin tai ovat vuorovaikutuksessa niiden kanssa. Käyttäytyäkseen homogeenisena materiaalina, jota kuvaa tarkasti efektiivinen taitekerroin, sen piirteiden on oltava paljon aallonpituutta pienempiä.

Mikroaaltosäteilyn osalta piirteet ovat millimetrien luokkaa. Mikroaaltotaajuiset metamateriaalit rakennetaan yleensä sähköä johtavien elementtien (kuten lankasilmukoiden) muodostamiksi ruuduiksi, joilla on sopivat induktiiviset ja kapasitiiviset ominaisuudet. Monissa mikroaaltotaajuuden metamateriaaleissa käytetään jaetun renkaan resonaattoreita.

Fotoniset metamateriaalit ovat rakenteeltaan nanometrin mittakaavassa ja manipuloivat valoa optisilla taajuuksilla. Fotoniset kiteet ja taajuusselektiiviset pinnat, kuten diffraktioristikot, dielektriset peilit ja optiset pinnoitteet, ovat samankaltaisia kuin aallonpituusrakenteiset metamateriaalit. Näitä pidetään kuitenkin yleensä metamateriaaleista erillisinä, koska niiden toiminta perustuu diffraktioon tai interferenssiin, eikä niitä siten voida approksimoida homogeeniseksi materiaaliksi. Fotonisten kiteiden kaltaiset materiaalirakenteet ovat kuitenkin tehokkaita näkyvän valon spektrissä. Näkyvän spektrin keskellä on aallonpituus noin 560 nm (auringonvalo). Fotoniset kiderakenteet ovat yleensä puolet tästä tai pienempiä, eli <280 nm.

Plasmoniset metamateriaalit hyödyntävät pintaplasmoneita, jotka ovat sähkövarauksen paketteja, jotka värähtelevät kollektiivisesti metallien pinnoilla optisilla taajuuksilla.

Frekvenssiselektiiviset pinnat (FSS, Frequency Selective Surfaces, FSS) voivat osoittaa aallonpituuksien alapuolella sijaitsevia piirteitä, ja ne tunnetaan monin eri tavoin nimillä keinotekoiset magneettiset johtimet (AMC, Artificial Magnetic Conductors) tai korkea-impedanssiset pinnat (High Impedance Surfaces, HIS). FSS:llä on induktiivisia ja kapasitiivisia ominaisuuksia, jotka liittyvät suoraan niiden aallonpituusrakenteeseen.

Elektromagneettiset metamateriaalit voidaan jakaa eri luokkiin seuraavasti:

Negatiivinen taitekerroinEdit

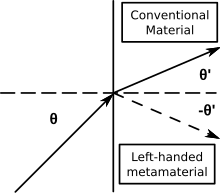
Pääartikkelit: Negatiivisen indeksin metamateriaali ja Negatiivinen taittuminen

Negatiivisen indeksin metamateriaaleille (NIM) on ominaista negatiivinen taitekerroin. Muita termejä NIM-materiaaleille ovat muun muassa ”vasenkätiset väliaineet”, ”väliaineet, joilla on negatiivinen taitekerroin” ja ”taaksepäin aaltoilevat väliaineet”. NIM:ejä, joissa negatiivinen taitekerroin syntyy samanaikaisesti negatiivisesta permittiivisyydestä ja negatiivisesta permeabiliteetista, kutsutaan myös kaksoisnegatiivisiksi metamateriaaleiksi tai kaksoisnegatiivisiksi materiaaleiksi (DNG, double negative materials).

Edellyttäen, että materiaalilla on hyvin approksimoituna reaalinen permittiivisyys ja permeabiliteetti, permittiivisyyden ϵ r \displaystyle \epsilon _{r}}:n välinen suhde.

, permeabiliteetin μ r {\displaystyle \mu _{r}}

ja taitekerroin n on n = ± ϵ r μ r {\displaystyle \scriptstyle n=\pm {\sqrt {\epsilon _{\mathrm {r}} }\mu _{\mathrm {r} }}}}

. Kaikilla tunnetuilla ei-metamateriaalisilla läpinäkyvillä materiaaleilla (lasi, vesi, …) on positiivinen ϵ r {\displaystyle \epsilon _{r}}

ja μ r {\displaystyle \mu _{r}}

. Konvention mukaan n:lle käytetään positiivista neliöjuurta. Joillakin teknisillä metamateriaaleilla on kuitenkin ϵ r {\displaystyle \epsilon _{r}}

ja μ r < 0 {\displaystyle \mu _{r}<0}

. Koska tuote ϵ r μ r {\displaystyle \epsilon _{r}\mu _{r}}

on positiivinen, n on reaalinen. Tällaisessa tilanteessa n:lle on otettava negatiivinen neliöjuuri. Kun sekä ϵ r {\displaystyle \epsilon _{r}} että {\displaystyle \epsilon _{r}}

ja μ r {\displaystyle \mu _{r}}

ovat positiivisia (negatiivisia), aallot kulkevat eteenpäin (taaksepäin). Sähkömagneettiset aallot eivät voi levitä materiaaleissa, joiden ϵ r {\displaystyle \epsilon _{r}}

ja μ r {\displaystyle \mu _{r}}

vastakkaisen merkin, kun taitekerroin muuttuu imaginaariseksi. Tällaiset materiaalit ovat läpinäkymättömiä sähkömagneettiselle säteilylle, ja esimerkkeinä ovat plasmoniset materiaalit, kuten metallit (kulta, hopea, …).

Edellä olevat tarkastelut ovat yksinkertaistettuja todellisille materiaaleille, joilla on oltava kompleksiarvoinen ϵ r {\displaystyle \epsilon _{r}}).

ja μ r {\displaystyle \mu _{r}}

. Sekä ϵ r {\displaystyle \epsilon _{r}} että ϵ r {\displaystyle \epsilon _{r}}:n reaaliosat ovat seuraavat.

ja μ r {\displaystyle \mu _{r}}

ei tarvitse olla negatiivisia, jotta passiivinen materiaali osoittaisi negatiivista taittumista. Itse asiassa negatiivinen taitekerroin ympyräpolarisoiduille aalloille voi syntyä myös kiraalisuudesta. Metamateriaaleilla, joilla on negatiivinen n, on lukuisia mielenkiintoisia ominaisuuksia:

• Snellin laki (n1sinθ1 = n2sinθ2) kuvaa edelleen taittumista, mutta koska n2 on negatiivinen, osuvat ja taittuvat säteet ovat pintanormaalin samalla puolella positiivisen ja negatiivisen indeksin omaavien materiaalien rajapinnalla.
• Tšerenkovin säteily osoittaa toiseen suuntaan.
• Aikakeskiarvoistettu Poyntingin vektori on vastakkaissuuntainen vaihenopeuteen nähden. Aaltojen (energian) eteneminen edellyttää kuitenkin, että -µ on parina -ε, jotta aaltoluvun riippuvuus materiaaliparametreista k c = ω μ ϵ {\displaystyle kc=\omega {\sqrt {\mu \epsilon }}}
  

  .

Negatiivinen taitekerroin juontuu matemaattisesti vektorikolmikosta E, H ja k.

Sähkömagneettisissa metamateriaaleissa eteneville tasoaalloille sähkökenttä, magneettikenttä ja aaltovektori noudattavat vasemmanpuoleista sääntöä, mikä on käänteistä perinteisten optisten materiaalien käyttäytymiseen verrattuna.

Tähän mennessä vain metamateriaaleilla on negatiivinen taitekerroin.

YksittäisnegatiivinenMuutos

Yksittäisnegatiivisilla (SNG) metamateriaaleilla on joko negatiivinen suhteellinen permittiivisyys (εr) tai negatiivinen suhteellinen permeabiliteetti (µr), mutta ei molempia. Ne toimivat metamateriaaleina, kun ne yhdistetään toiseen, täydentävään SNG:hen, jotka yhdessä toimivat DNG:nä.

Epsilon-negatiivisilla väliaineilla (ENG) on negatiivinen εr, kun µr on positiivinen. Monilla plasmoilla on tämä ominaisuus. Esimerkiksi jalometallit, kuten kulta tai hopea, ovat ENG infrapuna- ja näkyvässä spektrissä.

Mu-negatiivisilla väliaineilla (MNG) on positiivinen εr ja negatiivinen µr. Gyrotrooppisilla tai gyromagneettisilla materiaaleilla on tämä ominaisuus. Gyrotrooppinen materiaali on materiaali, joka on muuttunut kvasistaattisen magneettikentän vaikutuksesta, mikä mahdollistaa magneto-optisen vaikutuksen. Magnetooptinen ilmiö on ilmiö, jossa sähkömagneettinen aalto etenee tällaisen väliaineen läpi. Tällaisessa materiaalissa vasemmalle ja oikealle pyörivät elliptiset polarisaatiot voivat edetä eri nopeuksilla. Kun valo kulkee magneto-optisen materiaalikerroksen läpi, tulosta kutsutaan Faradayn efektiksi: polarisaatiotaso voi kääntyä, jolloin muodostuu Faradayn rotaattori. Tällaisen heijastuksen tuloksia kutsutaan magneto-optiseksi Kerr-ilmiöksi (ei pidä sekoittaa epälineaariseen Kerr-ilmiöön). Kahta gyrotrooppista materiaalia, joiden kahden pääpolarisaation pyörimissuunnat ovat päinvastaiset, kutsutaan optisiksi isomeereiksi.

ENG-materiaalista koostuvan laatan ja MNG-materiaalista koostuvan laatan yhdistäminen johti sellaisiin ominaisuuksiin kuin resonanssit, anomaalinen tunnelointi, läpinäkyvyys ja nollaheijastus. SNG-materiaalit ovat negatiivisen indeksin materiaalien tavoin luonnostaan dispersiivisiä, joten niiden εr, µr ja taitekerroin n, ovat taajuuden funktio.

HyperbolicEdit

Hyperboliset metamateriaalit (HMM) käyttäytyvät metallina tietylle polarisaatiolle tai valon etenemissuunnalle ja dielektrisinä toiselle negatiivisen ja positiivisen permittiivisyystensorikomponentin vuoksi, mikä antaa äärimmäistä anisotropiaa. Materiaalin dispersiosuhde aaltovektoriavaruudessa muodostaa hyperboloidin, ja siksi sitä kutsutaan hyperboliseksi metamateriaaliksi. HMM:n äärimmäinen anisotropia johtaa valon suuntautuneeseen etenemiseen pinnan sisällä ja pinnalla. HMM:t ovat osoittaneet erilaisia potentiaalisia sovelluksia, kuten aistiminen, kuvantaminen, optisten signaalien ohjaaminen, tehostetut plasmoniresonanssi-ilmiöt.

BandgapEdit

Elektromagneettiset bandgap-metamateriaalit (EBG tai EBM) ohjaavat valon etenemistä. Tämä tapahtuu joko fotonikiteillä (PC) tai vasenkätisillä materiaaleilla (LHM). PC:t voivat estää valon etenemisen kokonaan. Molemmat luokat voivat sallia valon etenemisen tiettyihin, suunniteltuihin suuntiin, ja molemmat voidaan suunnitella niin, että kaistanleveydet ovat halutuilla taajuuksilla. EBG:n jakson koko on huomattava osa aallonpituudesta, mikä aiheuttaa rakentavaa ja tuhoavaa interferenssiä.

PC eroaa aallonpituuden alapuolisista rakenteista, kuten viritettävistä metamateriaaleista, koska PC saa ominaisuutensa kaistaläpän ominaisuuksista. PC:t on mitoitettu vastaamaan valon aallonpituutta, toisin kuin muut metamateriaalit, jotka paljastavat aallonpituuden alittavan rakenteen. Lisäksi PC:t toimivat diffraktoimalla valoa. Sitä vastoin metamateriaali ei käytä diffraktiota.

PC:ssä on jaksollisia sulkeumia, jotka estävät aaltojen etenemisen sulkeumien hajonnan aiheuttaman tuhoavan interferenssin vuoksi. PC:n fotoninen bandgap-ominaisuus tekee niistä elektronisten puolijohdekiteiden sähkömagneettisen analogian.

EBG:n tavoitteena on luoda korkealaatuisia, vähähäviöisiä, jaksollisia, dielektrisiä rakenteita. EBG vaikuttaa fotoneihin samalla tavalla kuin puolijohdemateriaalit vaikuttavat elektroneihin. PC:t ovat täydellisiä bandgap-materiaaleja, koska ne eivät salli valon etenemistä. Jokainen määrätyn jaksollisen rakenteen yksikkö toimii kuin yksi atomi, vaikkakin paljon suuremman kokoisena.

EBG:t on suunniteltu estämään määrätyn kaistanleveyden taajuuksien eteneminen tietyillä saapumiskulmilla ja polarisaatioilla. EBG:n erityisominaisuuksien valmistamiseksi on ehdotettu erilaisia geometrioita ja rakenteita. Käytännössä on mahdotonta rakentaa virheetöntä EBG-laitetta.

EBG:tä on valmistettu taajuuksille, jotka vaihtelevat muutamasta gigahertsistä (GHz) muutamaan terahertsiin (THz), radio-, mikroaalto- ja infrapunataajuusalueille. EBG-sovellusten kehityskohteita ovat muun muassa siirtojohto, neliönmuotoisista dielektrisistä tangoista tehdyt puupaalut ja useat erityyppiset matalan vahvistuksen antennit.

Kaksoispositiivinen väliaineTiedosto

Kaksoispositiivisia väliaineita (DPS, Double Positive Medium) esiintyy luonnossa, kuten esimerkiksi luonnossa esiintyviä dielektrisiä aineita. Permittiivisyys ja magneettinen permeabiliteetti ovat molemmat positiivisia ja aaltojen eteneminen on etenemissuunnassa. On valmistettu keinotekoisia materiaaleja, joissa yhdistyvät DPS-, ENG- ja MNG-ominaisuudet.

Bi-isotrooppinen ja bianisotrooppinenMuokkaa

Kategorisoitaessa metamateriaaleja kaksinegatiivisiksi, yksinegatiivisiksi tai kaksinegatiivisiksi oletetaan tavallisesti, että metamateriaaleilla on toisistaan riippumattomat sähköiset ja magneettiset vasteet, joita kuvataan ε:llä ja µ:llä. Monissa tapauksissa sähkökenttä aiheuttaa kuitenkin magneettisen polarisaation, kun taas magneettikenttä indusoi sähköisen polarisaation, jota kutsutaan magneettisähköiseksi kytkennäksi. Tällaisia väliaineita nimitetään bi-isotrooppisiksi. Medioita, joissa esiintyy magnetosähköistä kytkentää ja jotka ovat anisotrooppisia (kuten monet metamateriaalirakenteet), kutsutaan bi-anisotrooppisiksi.

Bi-isotrooppisten medioiden magnetosähköiselle kytkennälle ovat ominaisia neljä materiaaliparametria. Ne ovat sähköinen (E) ja magneettinen (H) kentänvoimakkuus sekä sähköinen (D) ja magneettinen (B) vuontiheys. Nämä parametrit ovat ε, µ, κ ja χ eli permittiivisyys, permeabiliteetti, kiraalisuuden voimakkuus ja Tellegenin parametri. Tämäntyyppisissä väliaineissa materiaaliparametrit eivät muutu muuttuessaan pitkin kierrettyä mittauskoordinaatistoa. Tässä mielessä ne ovat invariantteja eli skalaarisia.

Sisäiset magnetosähköiset parametrit κ ja χ vaikuttavat aallon vaiheeseen. Kiraliteettiparametrin vaikutus on taitekertoimen jakaminen. Isotrooppisissa väliaineissa tämä johtaa aallon etenemiseen vain, jos ε ja µ ovat samanmerkkisiä. Bi-isotrooppisissa väliaineissa, joissa χ:n oletetaan olevan nolla ja κ:n nollasta poikkeava arvo, saadaan erilaisia tuloksia. Voi syntyä joko taaksepäin suuntautuva aalto tai eteenpäin suuntautuva aalto. Vaihtoehtoisesti voi esiintyä kaksi eteenpäin suuntautuvaa aaltoa tai kaksi taaksepäin suuntautuvaa aaltoa riippuen kiraalisuusparametrin voimakkuudesta.

Yleisessä tapauksessa bi-anisotrooppisten materiaalien konstitutiiviset suhteet ovat D = ϵ E + ξ H , {\displaystyle \mathbf {D} =\epsilon \mathbf {E} +\xi \mathbf {H} ,}

B = ζ E + μ H , {\displaystyle \mathbf {B} =\zeta \mathbf {E} +\mu \mathbf {H} ,}

missä ϵ {\displaystyle \epsilon }

ja μ {\displaystyle \mu } {\displaystyle \mu }

ovat vastaavasti permittiivisyys- ja permeabiliteettitensoreita, kun taas ξ {\displaystyle \xi }

ja ζ {\displaystyle \zeta }

ovat kaksi magnetosähköistä tensoria. Jos väliaine on vastavuoroinen, permittiivisyys ja permeabiliteetti ovat symmetrisiä tensoreita ja ξ = – ζ T = – i κ T {\displaystyle \xi =-\zeta ^{T}=-i\kappa ^{T}}

, missä κ {\displaystyle \kappa }

on kiraalinen tensori, joka kuvaa kiraalista sähkömagneettista ja vastavuoroista magnetosähköistä vastetta. Kiraalinen tensori voidaan ilmaista muodossa κ = 1 3 tr ( κ ) I + N + J {\displaystyle \kappa ={\tfrac {1}{3}}\operatorname {tr} (\kappa )I+N+J}}

, missä tr ( κ ) {\displaystyle \operatorname {tr} (\kappa )}

on jälki κ {\displaystyle \kappa } {\displaystyle \kappa }

, I on identiteettimatriisi, N on symmetrinen jälkivapaa tensori ja J on antisymmetrinen tensori. Tällaisen dekomposition avulla voimme luokitella vastavuoroisen bianisotrooppisen vasteen, ja voimme tunnistaa seuraavat kolme pääluokkaa: (i) kiraaliset väliaineet ( tr ( κ ) ≠ 0 , N ≠ 0 , J = 0 {\displaystyle \operatorname {tr} (\kappa )\neq 0,N\neq 0,J=0}}

), (ii) pseudokiraaliset väliaineet ( tr ( κ ) = 0 , N ≠ 0 , J = 0 {\displaystyle \operatorname {tr} (\kappa )=0,N\neq 0,J=0}}

), (iii) omega media ( tr ( κ ) = 0 , N = 0 , J ≠ 0 {\displaystyle \operatorname {tr} (\kappa )=0,N=0,J\neq 0}

).

ChiralEdit

Metamateriaalien kätisyys on potentiaalinen sekaannuksen lähde, sillä metamateriaalikirjallisuudessa termit vasen- ja oikeakätinen käytetään kahdella ristiriitaisella tavalla. Ensimmäinen viittaa jompaankumpaan kahdesta ympyräpolarisoidusta aallosta, jotka ovat eteneviä moodeja kiraalisissa väliaineissa. Toinen liittyy sähkökentän, magneettikentän ja Poyntingin vektorin triplettiin, joka syntyy negatiivisen taitekertoimen väliaineissa, jotka useimmissa tapauksissa eivät ole kiraalisia.

Yleisesti kiraalinen ja/tai bianisotrooppinen sähkömagneettinen vaste on seurausta 3D-geometrisestä kiraalisuudesta: 3D-kiraaliset metamateriaalit koostuvat upottamalla 3D-kiraalisia rakenteita isäntäväliaineeseen ja niissä esiintyy kiraalisuuteen liittyviä polarisaatioefektejä, kuten optista aktiivisuutta ja sirkulaarista dikroismia. Myös 2D-kiraliteetin käsite on olemassa, ja tasokappaleen sanotaan olevan kiraalinen, jos sitä ei voi asettaa päällekkäin peilikuvansa kanssa, ellei sitä nosteta tasosta. Anisotrooppisilla ja häviöllisillä 2D-kiraalisilla metamateriaaleilla on havaittu olevan ympyräpolarisoitujen aaltojen suuntaisesti epäsymmetristä läpäisyä (heijastusta, absorptiota) sirkulaarisen konversiodikroosin vuoksi. Toisaalta bianisotrooppinen vaste voi syntyä geometrisista akiraalisista rakenteista, joilla ei ole 2D- eikä 3D-intrinsistä kiraalisuutta. Plum ja kollegat tutkivat ekstrinsisestä kiraalisuudesta johtuvaa magneettisähköistä kytkentää, jossa (akiraalisen) rakenteen järjestys yhdessä säteilyn aaltovektorin kanssa poikkeaa sen peilikuvasta, ja havaitsivat suurta, säädettävissä olevaa lineaarista optista aktiivisuutta, epälineaarista optista aktiivisuutta, spekulaarista optista aktiivisuutta ja sirkulaarista konversiodikroismia. Rizza et al. ehdottivat 1D-kiraalisia metamateriaaleja, joissa efektiivinen kiraalinen tensori ei ole häviävä, jos systeemi on geometrisesti yksiulotteisen kiraalinen (koko rakenteen peilikuvaa ei voida asettaa siihen päällekkäin käyttämällä translaatioita ilman rotaatioita).

3D-kiraalisia metamateriaaleja rakennetaan kiraalisista materiaaleista tai resonaattoreista, joissa efektiivinen kiraalisuusparametrin κ \displaystyle \kappa }

on nollasta poikkeava. Aaltojen etenemisominaisuudet tällaisissa kiraalisissa metamateriaaleissa osoittavat, että negatiivinen taittuminen voidaan toteuttaa metamateriaaleissa, joilla on voimakas kiraalisuus ja positiivinen ϵ r {\displaystyle \epsilon _{r}}

ja μ r {\displaystyle \mu _{r}}

. Tämä johtuu siitä, että taitekerroin n {\displaystyle n}

on erilaiset arvot vasemmalle ja oikealle ympyräpolarisoidulle aallolle, joka saadaan kaavalla

n = ± ϵ r μ r ± κ {\displaystyle n=\pm {\sqrt {\epsilon _{r}\mu _{r}}}\pm \kappa }

Voidaan nähdä, että yhdelle polarisaatiolle syntyy negatiivinen indeksi, jos κ {\displaystyle \kappa }

> ϵ r μ r {\displaystyle {\sqrt {\epsilon _{r}\mu _{r}}}}

. Tällöin ei ole välttämätöntä, että jompikumpi tai molemmat ϵ r {\displaystyle \epsilon _{r}}

ja μ r {\displaystyle \mu _{r}}

ovat negatiivisia taaksepäin suuntautuvan aallon etenemiselle. Kiraliteetista johtuvan negatiivisen taitekertoimen havaitsivat ensimmäisen kerran samanaikaisesti ja toisistaan riippumatta Plum et al. ja Zhang et al. vuonna 2009.

FSS-pohjainenEdit

Taajuusselektiiviseen pintaan perustuvat metamateriaalit estävät signaalit yhdellä aaltokaistalla ja päästävät ne läpi toisella aaltokaistalla. Niistä on tullut vaihtoehto kiinteän taajuuden metamateriaaleille. Ne mahdollistavat valinnaiset taajuusmuutokset yhdessä väliaineessa kiinteän taajuusvasteen rajoittavien rajoitusten sijaan.