Yleistettyjen lineaaristen mallien opetusohjelmassa tutustuimme erilaisiin GLM-malleihin, kuten lineaariseen regressioon, logistiseen regressioon jne. Tässä TechVidvanin R-opetussarjan opetusohjelmassa tarkastelemme yksityiskohtaisesti lineaarista regressiota R:ssä. Opimme, mitä on R lineaarinen regressio ja miten se toteutetaan R:ssä. Tarkastelemme pienimmän neliösumman estimointimenetelmää ja opimme myös, miten mallin tarkkuus tarkistetaan.

Siinä, ilman muuta, aloitetaan!

Lineaarinen regressio R:ssä

Lineaarinen regressio R:ssä on menetelmä, jota käytetään ennustamaan muuttujan arvoa yhden tai useamman syöttöennustemuuttujan arvon tai arvojen avulla. Lineaarisen regression tavoitteena on luoda lineaarinen suhde halutun tulomuuttujan ja tuloennustemuuttujien välille.

Mallinnetaan jatkuva muuttuja Y yhden tai useamman tuloennustemuuttujan Xi funktiona siten, että funktiota voidaan käyttää ennustamaan Y:n arvoa, kun vain Xi:n arvot tunnetaan. Tällaisen lineaarisen suhteen yleinen muoto on:

Y=?0+?1 X

Tässä ?0 on leikkauspiste
ja ?1 on kaltevuus.

Lineaarisen regression tyypit R:ssä

R:n lineaarisen regression tyyppejä on kaksi:

• yksinkertainen lineaarinen regressio
• moninkertainen lineaarinen regressio

Katsotaan näitä yksitellen.

Yksinkertainen lineaarinen regressio R:ssä

Yksinkertaisen lineaarisen regression tarkoituksena on löytää lineaarinen suhde kahden jatkuvan muuttujan välille. On tärkeää huomata, että suhde on luonteeltaan tilastollinen eikä deterministinen.

Deterministinen suhde on sellainen, jossa yhden muuttujan arvo voidaan löytää tarkasti toisen muuttujan arvon avulla. Esimerkki deterministisestä suhteesta on kilometrien ja mailien välinen suhde. Käyttämällä kilometrin arvoa voimme löytää tarkasti etäisyyden maileina. Tilastollinen suhde ei ole tarkka ja siinä on aina ennustusvirhe. Esimerkiksi, kun annetaan riittävästi tietoja, voimme löytää henkilön pituuden ja painon välisen suhteen, mutta siinä on aina virhemarginaali ja poikkeustapauksia on olemassa.

Yksinkertaisen lineaarisen regression ideana on löytää viiva, joka parhaiten sopii molempien muuttujien annettuihin arvoihin. Tämä viiva voi sitten auttaa meitä löytämään riippuvan muuttujan arvot silloin, kun ne puuttuvat.

Tutkitaan tätä esimerkin avulla. Meillä on tietokokonaisuus, joka koostuu 500 ihmisen pituuksista ja painoista. Tavoitteenamme on rakentaa lineaarinen regressiomalli, joka muotoilee pituuden ja painon välisen suhteen siten, että kun annamme pituuden (Y) syötteenä malliin, se voi antaa meille vastineeksi painon (X) mahdollisimman pienellä virhemarginaalilla.

Y=b0+b1X

B0:n ja b1:n arvot on valittava siten, että ne minimoivat virhemarginaalin. Virhemittarin avulla voidaan mitata mallin tarkkuutta.

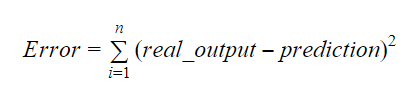
Voidaan laskea kaltevuus tai kerroin seuraavasti:
Virhemittarin kerroin R
Virhemittari R
B1:n arvo antaa meille tietoa riippuvaisen ja riippumattoman muuttujan välisen suhteen luonteesta.

• Jos b1 > 0, muuttujilla on positiivinen suhde ts. x:n kasvu johtaa y:n kasvuun.
• Jos b1 < 0, muuttujilla on negatiivinen suhde eli x:n kasvu johtaa y:n vähenemiseen.

B0:n eli interceptin arvo voidaan laskea seuraavasti: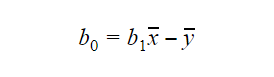
B0:n arvo voi myös antaa paljon tietoa mallista ja päinvastoin.

Jos mallissa ei ole x=0, niin ennuste on merkityksetön ilman b1:tä. Jotta mallissa olisi jossakin pisteessä vain b0 eikä b1, x:n arvon on oltava kyseisessä pisteessä 0. Esimerkiksi pituuden tapauksessa x ei voi olla 0, eikä ihmisen pituus voi olla 0. Siksi tällainen malli on merkityksetön, jos siinä on vain b0.

Jos b0-termi puuttuu, malli kulkee origon kautta, mikä tarkoittaa, että ennuste ja regressiokerroin (kaltevuus) ovat vääristyneitä.

Multiple Lineaarinen regressio R:ssä

Multiple Lineaarinen regressio on yksinkertaisen lineaarisen regression laajennus. Moninkertaisessa lineaarisessa regressiossa pyritään luomaan lineaarinen malli, jolla voidaan ennustaa kohdemuuttujan arvo käyttämällä useiden ennustemuuttujien arvoja. Tällaisen funktion yleinen muoto on seuraava:

Y=b0+b1X1+b2X2+…+bnXn

Mallin tarkkuuden arviointi

Mallin laadun ja tarkkuuden arviointiin on erilaisia menetelmiä. Tarkastellaan joitakin näistä menetelmistä yksi kerrallaan.

R-neliö

Datan todellinen informaatio on sen välittämä varianssi. R-kvartiili kertoo, kuinka suuren osan kohdemuuttujan (y) vaihtelusta malli selittää. Voimme löytää mallin R-kvartiilimittarin seuraavan kaavan avulla: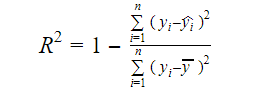

Jossa,

• yi on y:n sovitettu arvo havainnolle i
• y on Y:n keskiarvo.

Matalampi R-kvartiilimuuttujan arvo merkitsee mallin alhaisempaa tarkkuutta. R-kvartiilimittari ei kuitenkaan välttämättä ole lopullinen ratkaiseva tekijä.

Oikaistu R-kvartiili

Kun muuttujien määrä mallissa kasvaa, kasvaa myös R-kvartiilin arvo. Tämä aiheuttaa myös virheitä äskettäin lisättyjen muuttujien selittämään vaihteluun. Siksi mukautamme R-neliön kaavaa useiden muuttujien osalta.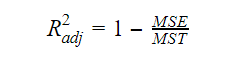
Tässä MSE tarkoittaa keskivirhettä, joka on:

Ja MST tarkoittaa keskivirhettä, joka saadaan kaavasta: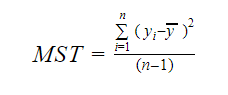

Jossa n tarkoittaa havaintojen lukumäärää ja q kertoimien lukumäärää.

R-squaredin ja oikaistun R-squaredin suhde on: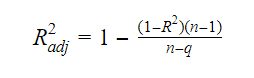

Standardivirhe ja F-statistiikka

Standardivirhe ja F-statistiikka ovat kumpikin mallin sopivuuden laadun mittareita. Standardivirheen ja F-statistiikan kaavat ovat:

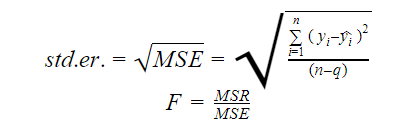
Jossa MSR on lyhenne sanoista Mean Square Regression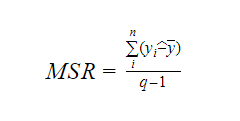

AIC ja BIC

Akaiken informaatiokriteeri (Akaiken informaatiokriteeri) ja Bayesin informaatiokriteeri (Bayesin informaatiokriteeri) ovat tilastollisten mallien soveltuvuuden laadun mittauksia. Niitä voidaan käyttää myös mallin valintakriteereinä.

AIC=(-2)*ln(L)+2*k
BIC=(-2)*ln(L)+k*ln(n)

Jossa,

• L on todennäköisyysfunktio,
• k on malliparametrien lukumäärä,
• n on otoskoko.

lm-funktio R:ssä

R:n lm()-funktio sovittaa lineaarisia malleja. Se voi suorittaa regression sekä varianssi- ja kovarianssianalyysin. Lm-funktion syntaksi on seuraava:

lm(formula, data, subset, weights, na.action,method = "qr", model = TRUE, x = FALSE, y = FALSE, qr = TRUE,singular.ok = TRUE, offset, …)

Jossa,

• formula on luokan ”formula” objekti ja on sovitettavan mallin symbolinen esitys,
• data on datakehys tai -luettelo, joka sisältää kaavan muuttujat(data on valinnainen argumentti. Jos se puuttuu, funktio poimii muuttujat ympäristöstä),
• subset on valinnainen vektori, joka sisältää sovitusprosessissa käytettävän havaintojen osajoukon,
• weights on valinnainen vektori, joka määrittää sovitusprosessissa käytettävät painot,
• na.action on funktio, joka osoittaa, mitä pitäisi tapahtua, kun datassa esiintyy NA:ta,
• method tarkoittaa menetelmää, jolla malli sovitetaan,
• model, x, y ja qr ovat loogisia lausekkeita, jotka kontrolloivat sitä, palautetaanko vastaavat arvot ulostulon mukana vai ei. Nämä arvot ovat:
• model: mallin kehys
• x: mallin matriisi
• y: vaste
• qr: qr-dekompositio
• singular.ok on logiikka, joka kontrolloi sallitaanko singulaariset sovitukset vai ei,
• offset on ennalta tunnettu ennustaja, jota tulisi käyttää mallissa,
• . . ovat lisäargumentteja, jotka välitetään alemman tason regressiofunktioille.

Käytännön esimerkki lineaarisesta regressiosta R:ssä

Tässä riittää teoriaa toistaiseksi. Katsotaanpa, miten tämä kaikki toteutetaan. Sovitamme lineaarisen mallin käyttämällä lineaarista regressiota R:ssä lm()-funktion avulla. Tarkistamme jälkikäteen myös mallin sopivuuden laadun. Käytetään autojen tietokokonaisuutta, joka on oletusarvoisesti mukana R-peruspaketissa.

1. Aloitetaan datasetin graafisella analyysillä, jotta tutustumme siihen paremmin. Tätä varten piirretään hajontakuvio ja tarkistetaan, mitä se kertoo meille datasta.

Voimme käyttää funktiota scatter.smooth() luodaksemme hajontakuvion datasetille.

scatter.smooth(x=cars$speed,y=cars$dist,main="TechVidvan Dist ~ Speed")

Tulos

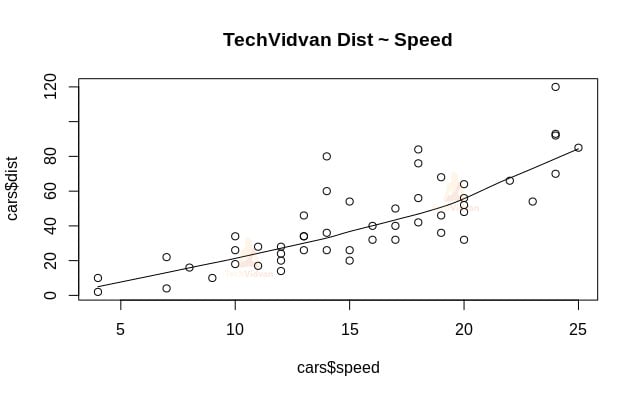
Scatter Plot osoittaa meille positiivisen korrelaation matkan ja nopeuden välillä. Se viittaa lineaarisesti kasvavaan suhteeseen näiden kahden muuttujan välillä. Tämä tekee aineistosta sopivan lineaarista regressiota varten, sillä lineaarinen suhde on perusoletus sovitettaessa lineaarista mallia aineistoon.

2. Nyt kun olemme varmistaneet, että lineaarinen regressio sopii aineistoon, voimme käyttää lm()-funktiota sovittaaksemme siihen lineaarisen mallin.

Linear_model <- lm(dist~speed,data=cars)print(Linear_model)

Tulos

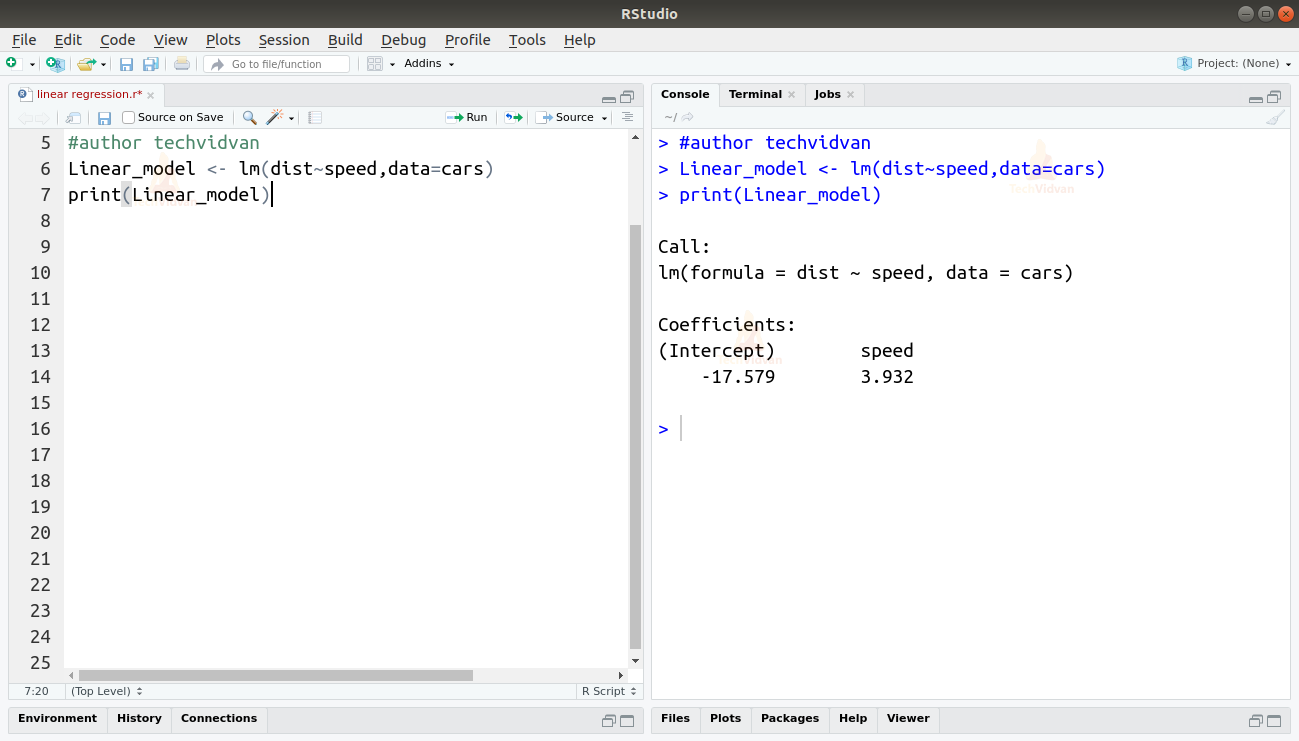
Lm()-funktion tulosteesta näemme leikkauspisteen ja nopeuskertoimen. Näin määritetään lineaarinen yhteys etäisyyden ja nopeuden välille seuraavasti:

Etäisyys=Sisäpiste+kerroin*nopeus

Etäisyys=-17,579+3,932*nopeus

3. Nyt kun olemme sovittaneet mallin, tarkistetaan sovituksen laatu tai hyvyys. Aloitetaan tarkastamalla lineaarisen mallin yhteenveto käyttämällä summary()-funktiota.

summary(Linear_model)

Output

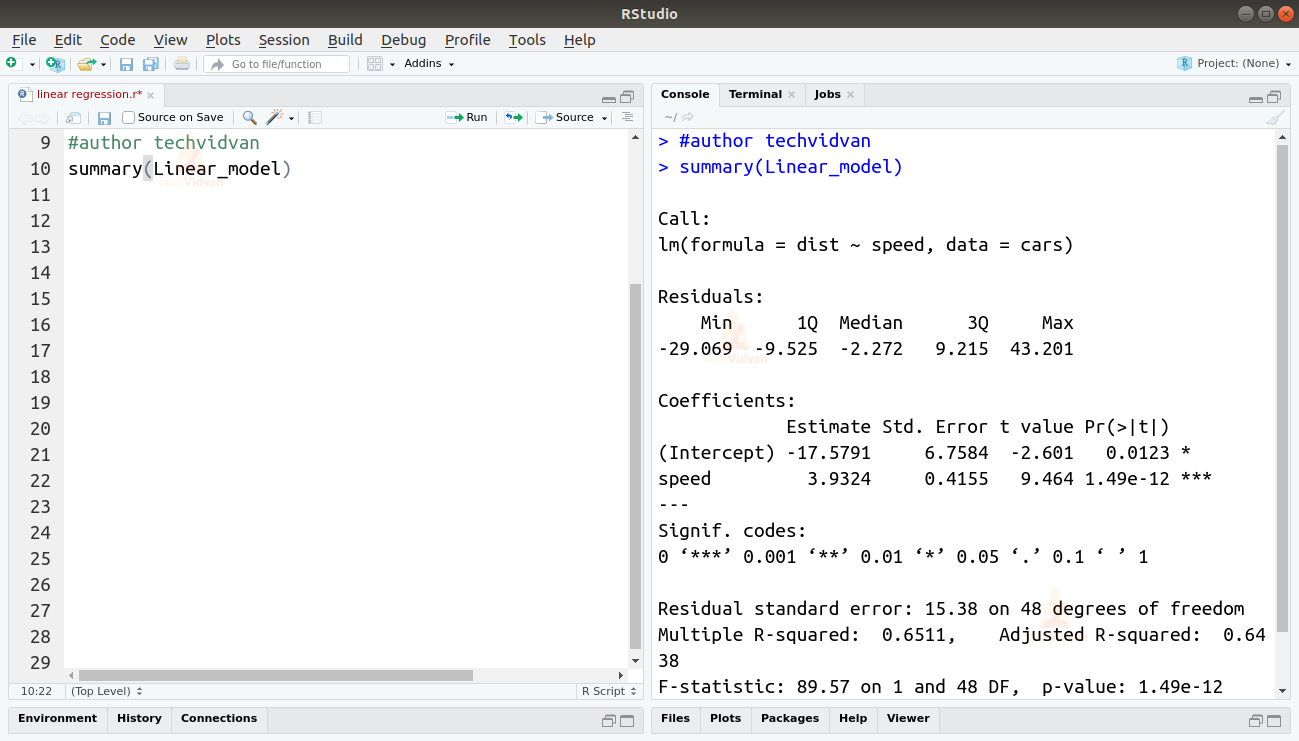
Summary()-funktio antaa meille muutamia tärkeitä mittareita, joiden avulla voimme diagnosoida mallin sopivuutta. P-arvo on tärkeä mittari mallin sopivuuden hyvyydelle. Mallin sanotaan olevan sopimaton, jos p-arvo on suurempi kuin ennalta määritetty tilastollinen merkitsevyystaso, joka on ihanteellisesti 0,05.

Yhteenveto antaa meille myös t-arvon. Mitä suurempi t-arvo on, sitä paremmin malli sopii.
Voidaan myös löytää AIC- ja BIC-arvot käyttämällä AIC()- ja BIC()-funktioita.

AIC(Linear_model)BIC(Linear_model)

Tulos

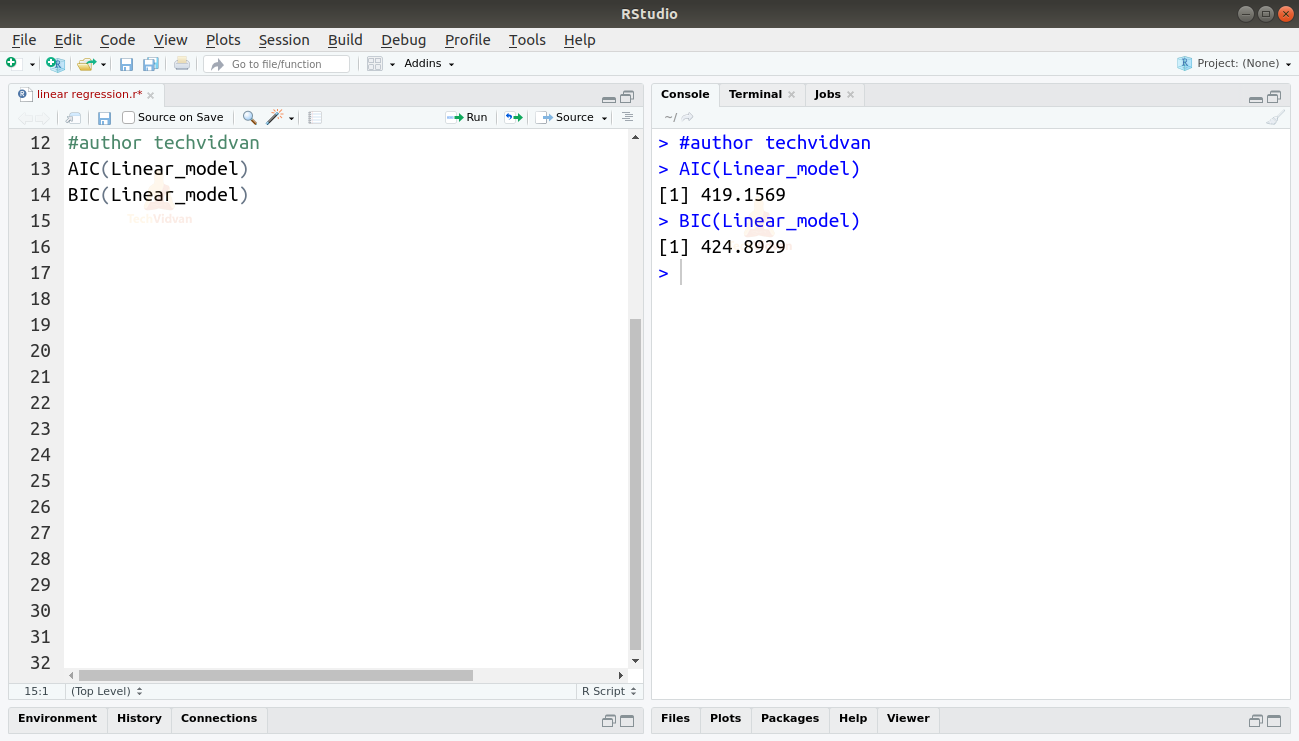
Malli, joka tuottaa pienimmät AIC- ja BIC-pisteet, on suositeltavin.

Yhteenveto

Tässä TechVidvan R-opetussarjan luvussa opimme lineaarisesta regressiosta. Opimme yksinkertaisesta lineaarisesta regressiosta ja moninkertaisesta lineaarisesta regressiosta. Sitten tutkimme erilaisia mittareita mallin laadun tai tarkkuuden arvioimiseksi, kuten R2, korjattu R2, keskivirhe, F-statistiikka, AIC ja BIC. Sitten opimme, miten lineaarinen regressio toteutetaan R:ssä. Sitten tarkistimme mallin sopivuuden laadun R:ssä.

Jaa arvosanasi Googlessa, jos pidit lineaarisen regression opetusohjelmasta.