
Tässä artikkelissa esittelen laadun ylläpitämisen perusteet.
Tähän kuuluvat laadunvarmistus, laadunvalvonta ja metrologia. Käytämme laadunvarmistusta saadaksemme varmuuden siitä, että laatuvaatimukset täyttyvät. Laadunvalvontaa käytetään sen tarkistamiseen, että vaatimukset on täytetty. Tämä on hienovarainen ero, ja käytännössä termejä käytetään joskus vaihdellen. Metrologia on mittaustiedettä. Sen avulla varmistamme, että voimme varmuudella vertailla eri puolilla maailmaa tehtyjen mittausten tuloksia.
Näitä periaatteita voidaan soveltaa tuotteisiin tai palveluihin, mutta aion keskittyä valmistukseen ja siihen, miten nämä kolme peruskäsitettä liittyvät toisiinsa siinä yhteydessä. Olen siksi välttänyt tiettyjen menetelmien yksityiskohtia enkä mene mihinkään matematiikkaan. Säästän sen myöhempään artikkeliin.
Mittaamisen alkuperä
Egyptiläiset käyttivät mittanormaaleja ja säännöllisiä kalibrointeja varmistaakseen, että kivet sopivat toisiinsa suurissa rakennushankkeissaan. Nykyaikaiset laatujärjestelmät alkoivat kuitenkin toden teolla teollisen vallankumouksen aikana. Sitä ennen mekaanisia tuotteita rakensivat käsityöläiset, jotka hioivat jokaisen osan erikseen, jotta se sopisi kokoonpanoon. Tämä tarkoitti, että jokainen kone ja sen jokainen osa oli ainutlaatuinen. Jos jokin osa oli vaihdettava, käsityöläisen oli asennettava uusi osa.
1700-luvun lopulla ranskalaiset asevalmistajat alkoivat valmistaa musketteja, joissa oli vakio-osat. Näin armeija pystyi kantamaan mukanaan varaosia ja vaihtamaan ne nopeasti rikkinäisiin. Nämä vaihdettavat osat sovitettiin edelleen kokoonpanoon, mutta sen sijaan, että kukin osa olisi sovitettu yksittäiseen aseeseen, se sovitettiin master-osaan .
Muutamaa vuotta myöhemmin amerikkalaiset asevalmistajat alkoivat käyttää tätä menetelmää, mutta sovittivat sen heidän kouluttamattomille työntekijöilleen sopivaksi. He viilasivat mittoja sovitettavaksi master-osaan, työntekijät asensivat jigit ja tuotantokoneet mittojen avulla ja käyttivät mittoja myös osien tarkistamiseen. Tämä mahdollisti sen, että rivi koneita, joista kukin suoritti yhden toiminnon ammattitaidottoman käyttäjän kanssa, pystyi tuottamaan tarkkoja osia. Osat voitiin sitten nopeasti koota monimutkaisiksi koneiksi.
Nykyaikaisen valmistuksen perusta oli siis luotu yli 100 vuotta ennen kuin Ford sovelsi näitä ideoita liikkuvaan tuotantolinjaan.
Kalibrointi, todellinen arvo ja mittausvirhe
Pääosien, mittalaitteiden ja kertakäyttökoneiden järjestelmä toimi, kun koko tuote valmistettiin yhdessä tehtaassa. Nykyaikaiset globaalit toimitusketjut tarvitsevat toisenlaisen järjestelmän.
Fyysisen master-osan sijaan meillä on piirustus tai digitaalinen CAD-malli. Määritetyt toleranssit varmistavat, että osat sopivat yhteen ja toimivat tarkoitetulla tavalla. Sen sijaan, että jokainen valmistaja tulisi yhdelle master-osalle asettamaan mittalaitteitaan, ne kalibroivat mittalaitteitaan. Mittalaitteita käytetään sitten tuotantokoneiden säätämiseen ja tuotettujen osien tarkastamiseen.
Kaikki laatu riippuu tästä kalibrointiprosessista.
Tärkein käsite, joka on ymmärrettävä, on se, että kaikissa mittauksissa on epävarmuutta. Jos pyytäisin sinua arvioimaan tämän tekstin korkeuden, saattaisit sanoa: ” se on noin 4 mm” . Sanan ’noin’ käyttäminen viittaa siihen, että arviossasi on jonkin verran epävarmuutta.
Itse asiassa emme voi koskaan tietää minkään asian tarkkaa todellista arvoa, kaikki mittaukset ovat itse asiassa arvioita, ja niihin liittyy jonkin verran epävarmuutta. Mittaustuloksen ja todellisen arvon välinen ero on mittausvirhe . Koska emme voi tietää todellista arvoa, emme voi tietää myöskään virhettä: nämä ovat tuntemattomia suureita.
Kaikki mitä voimme kvantifioida ympäröivästä maailmasta, ovat mittaustulokset, ja niihin liittyy aina jonkin verran epävarmuutta, vaikka tämä epävarmuus olisikin hyvin pieni.
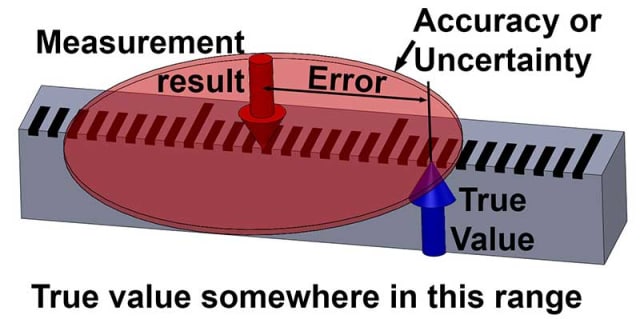
Jos arvioit tämän tekstin korkeudeksi ” noin 4 mm, plus miinus 1 mm”, olet nyt asettanut epävarmuudellesi joitakin rajoja. Mutta et silti voi olla 100-prosenttisen varma, että se pitää paikkansa.
Sinulla saattaa olla jokin luottamustaso, vaikkapa 95 prosenttia, että se on totta. Jos kasvattaisit rajoja, vaikkapa enemmän tai vähemmän 2 mm , niin luottamuksesi kasvaisi, ehkä 99 prosenttiin. Epävarmuus antaa siis joitakin rajoja, joiden sisällä meillä on luottamustaso, että todellinen arvo on.
OK, filosofian tunti ohi!
Tulevassa postauksessa laajennan näitä ajatuksia ja miten epävarmuus tietylle luottamustasolle voidaan laskea.
Epävarmuus ja laatu
Kun olemme määritelleet mittauksen epävarmuuden (tai ”tarkkuuden”), voimme soveltaa sitä päättäessämme, onko osa tietyn toleranssin mukainen. Sanotaan esimerkiksi, että osan on määritetty olevan 100 mm +/- 1 mm. Mittaamme sen ja saamme tulokseksi 100,87 mm.
Onko osa spesifikaation mukainen?
Yksinkertainen vastaus on: ”Emme tiedä, ehkä se on, mutta ehkä mittauksessamme oli virhe ja itse asiassa osa on yli 101 mm. Ehkä oli vielä suurempi virhe ja osa on itse asiassa pienempi kuin 99 mm!””
Ellemme tiedä, mikä on mittauksen epävarmuus, meillä ei ole aavistustakaan, kuinka varmoja voimme olla siitä, että osa on spesifikaation sisällä. Oletetaan, että mittauksen epävarmuus annettiin siten, että mittaustulos on 100,87 mm +/- 0,1 mm 95 prosentin varmuudella. Nyt voimme sanoa paremmalla kuin 95 prosentin varmuudella, että osa on spesifikaation sisällä.
Mittausten epävarmuuden ymmärtäminen ja kvantifiointi on siis kriittinen tekijä laadun ylläpitämisessä.
Tarkastellaan nyt kalibrointia ja siihen liittyvää jäljitettävyyden käsitettä. Tämä on epävarmuuden perustavanlaatuinen näkökohta. Kalibrointi on vertailu referenssiin, ja tämän vertailun epävarmuus on aina sisällytettävä, jäljempänä selitettävistä syistä.
Jäljitettävissä oleva mittaus on mittaus, jolla on katkeamaton kalibrointien ketju, joka ulottuu aina ensisijaiseen standardiin asti. Pituusmittausten tapauksessa ensisijainen standardi on metrin määritelmä; etäisyys, jonka valo kulkee tyhjiössä 1/299,792,458 sekunnissa, sellaisena kuin Pariisissa sijaitseva kansainvälinen paino- ja mittatoimisto (BIPM) on sen toteuttanut.
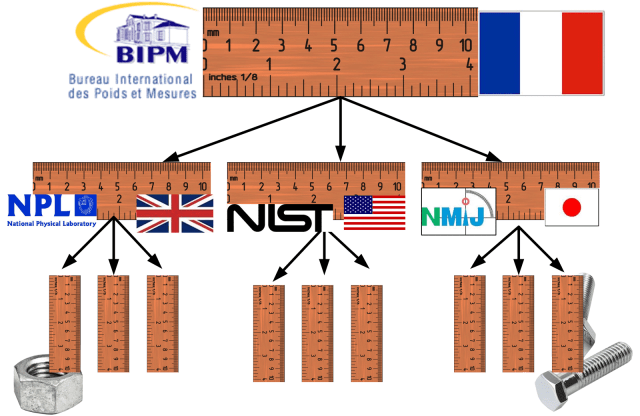
1930-luvulta lähtien tuuma on määritelty 25,4 mm:ksi ja on siten myös jäljitettävissä samaan metrin standardiin. Kaikkien mittausten on oltava jäljitettävissä samaan standardiin, jotta voidaan varmistaa, että eri maissa valmistetut osat sopivat yhteen.
Epävarmuus ja virhe
Mittausten epävarmuus syntyy eri lähteistä. Osa niistä aiheuttaa tulokseen johdonmukaisen virheen eli harhan.
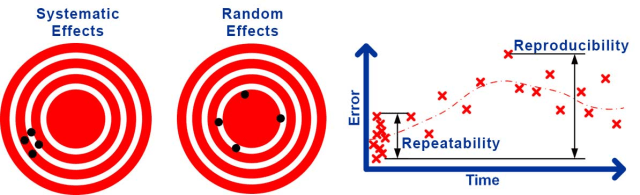
Esimerkiksi mittalaitteen kalibroinnissa esiintyvä tuntematon virhe johtaa johdonmukaiseen virheeseen aina, kun sitä käytetään. Tällaista vaikutusta kutsutaan systemaattiseksi epävarmuudeksi, joka johtaa systemaattiseen virheeseen . Muut lähteet johtavat virheisiin, jotka muuttuvat satunnaisesti joka kerta, kun mittaus tehdään.
Esimerkiksi ilman turbulenssi voi aiheuttaa pieniä, satunnaisesti muuttuvia häiriöitä lasermittauksiin, mekaaninen peli ja kohdistus voivat aiheuttaa satunnaisesti muuttuvia virheitä mekaanisiin mittauksiin. Tämäntyyppistä vaikutusta kutsutaan satunnaiseksi epävarmuudeksi, joka johtaa satunnaiseen virheeseen .
On tavanomaista jakaa satunnainen epävarmuus toistettavuuteen , tulosten satunnainen epävarmuus samoissa olosuhteissa, ja toistettavuuteen , satunnainen epävarmuus muuttuneissa olosuhteissa.
Olosuhteet eivät tietenkään voi koskaan olla täsmälleen samat tai täysin erilaiset, joten erottelu on hieman epämääräinen. Olosuhteita, joita voidaan muuttaa, ovat mittauksen tekeminen eri aikaan, eri operaattorilla, eri laitteella, eri kalibrointia käyttäen ja eri ympäristössä.
Mittauksen epävarmuuden kvantifiointiin on kaksi yleisesti käytettyä menetelmää. Kalibrointilaboratoriot ja tieteelliset laitokset suorittavat tavallisesti epävarmuuden arvioinnin Guide to the Expression of Uncertainty in Measurement (GUM) -oppaan mukaisesti.
GUM-menetelmässä otetaan ensin huomioon kaikki ne tekijät, jotka voivat vaikuttaa mittaustulokseen. Tämän jälkeen on määritettävä matemaattinen malli, joka antaa mittaustuloksen näiden vaikutussuureiden funktiona. Tarkastelemalla kunkin syöttösuureen epävarmuutta ja soveltamalla ”epävarmuuden leviämislakia” voidaan laskea arvio mittauksen yhdistetystä epävarmuudesta.
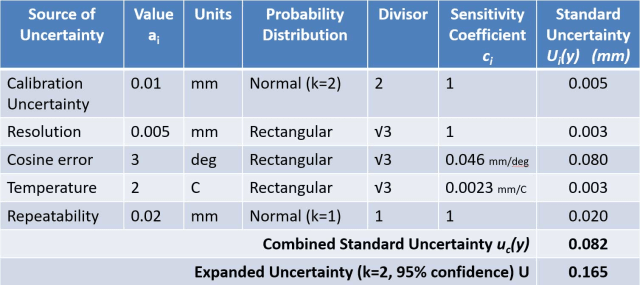
GUM-lähestymistapaa kuvataan joskus alhaalta ylöspäin -lähestymistavaksi, koska se alkaa jokaisen yksittäisen vaikutussuureen tarkastelulla. Jokainen vaikutus luetellaan yleensä taulukossa, jota kutsutaan epävarmuusbudjetiksi ja jota käytetään yhdistetyn epävarmuuden laskemiseen.
Teollisuuden mittausprosesseja arvioidaan tyypillisesti käyttäen mittausjärjestelmäanalyysia (Measurement Systems Analysis, MSA), jota suositellaan Six-Sigma-menetelmässä, ja tavallisesti noudattaen Automotive Industry Action Groupin (AIAG) MSA-viitekäsikirjan ohjeita .
MSA:ssa suoritetaan mittatutkimuksia, joissa toistuvia mittauksia verrataan referenssiin eri olosuhteissa harhan, toistettavuuden ja joskus toistettavuuden määrittämiseksi.
Tyypin 1 mittalaitetutkimus on pikatarkastus, joka yleensä tehdään mittalaitteen vaihtelun ymmärtämiseksi aluksi. Siinä yksi käyttäjä mittaa yhden kalibroidun vertailukappaleen 25 tai useampia kertoja ja tarkastelee sitten tulosten vaihtelua ja harhaa. Tämäntyyppistä testiä kutsutaan usein toistettavuustutkimukseksi MSA:n ulkopuolella.
Mittauksen toistettavuus- ja uusittavuustutkimusta (Gage R&R) käytetään, kun halutaan saada yksityiskohtaisempi käsitys mittausprosessista. Tyypillisesti 10 osaa mitataan kahdesti vähintään kolmen eri käyttäjän toimesta. Tämän jälkeen käytetään ANOVA-nimistä tilastollista menetelmää sen määrittämiseksi, kuinka suuri osa vaihtelusta johtuu mittalaitteesta (”gage”) ja kuinka suuri osa operaattorista. Tällöin katsotaan, että käyttäjän vaihtuminen ja sitä seuraavat muutokset ajassa ja ympäristössä edustavat täydellisesti uusittavuusolosuhteita.
MSA:ta kutsutaan joskus ylhäältä alaspäin suuntautuvaksi, koska siinä käsitellään mittausprosessia suurelta osin mustana laatikkona ja määritetään kokeellisesti systemaattiset ja satunnaiset epävarmuudet. Kaksi tärkeää käsitettä MSA:ssa ovat tarkkuus , jota käytetään epävarmuuden vastineena, ja tarkkuus , jota käytetään satunnaisen epävarmuuden vastineena.
Epävarmuuden arvioinnin etuna on, että se pystyy ottamaan huomioon kaikki epävarmuuden lähteet ja antaa oikein tehtynä tarkimman arvion epävarmuudesta. Tämän lähestymistavan ongelmiin kuuluu se, että se vaatii metrologin, joka pystyy tuottamaan matemaattisen mallin, ja inhimillisen erehdyksen riski, joka johtaa siihen, että merkittäviä vaikutteita jätetään pois tai arvioidaan väärin.
GUM-menetelmä pätee myös vain yksittäiseen mittaukseen, joka on suoritettu siten, että kaikkien käytettyjen korjausten arvot tunnetaan. Siksi epävarmuuden arviointia on vaikea soveltaa oikein teollisen mittausprosessin epävarmuuden ennustamiseen.
MSA-menetelmää voidaan soveltaa paljon helpommin, ja sen tarkoituksena on antaa ennuste teollisen mittausprosessin tarkkuudesta. Tämän lähestymistavan ongelmana on, että tietyt systemaattiset vaikutukset jätetään huomiotta ja uusittavuusolosuhteet eivät välttämättä ole täysin edustettuina, mikä johtaa epävarmuuden aliarviointiin.
Esimerkki systemaattisten vaikutusten huomiotta jättämisestä on se, että harhaa määritettäessä tehdään vertailu referenssiin, jota pidetään todellisena arvona – todellisuudessa referenssissä on myös epävarmuutta, joka pitäisi ottaa huomioon. Tämä menetelmä perustuu siihen, että kaikkia uusittavuusolosuhteita vaihdellaan siten, että niiden vaikutukset näkyvät tulosten vaihtelussa toistomittauksia tehtäessä. On todennäköistä, että tapa, jolla näitä olosuhteita vaihdellaan, ei täysin vastaa todellisen mittausprosessin aikana tapahtuvaa vaihtelua.
Mittaaminen ja laadunvarmistus
Tähän mennessä olen keskittynyt laadunvalvontaan eli siihen, miten mittauksilla voidaan todistaa osien vaatimustenmukaisuus sen jälkeen, kun ne on valmistettu. Tarkastellaan nyt lyhyesti laadunvarmistusta, eli tapaa, jolla varmistetaan, että prosessi ylipäätään tuottaa hyviä osia.
Tätä laadun näkökulmaa käsitellään suurelta osin tilastollisessa prosessinohjauksessa (SPC) . Prosessia voidaan arvioida valmistamalla useita osia ja mittaamalla ne valmistusprosessin vaihtelun ja harhan määrittämiseksi. Sen sijaan, että nämä tulokset annettaisiin suoraan, on tavallista jakaa osan toleranssi prosessin tarkkuudella, jolloin saadaan työstökoneen kapasiteetti ( C P ), tai prosessin tarkkuudella, jolloin saadaan prosessin kapasiteetti ( C PK ).
SPC vastaa monin tavoin MSA:ta. Siinä käytetään ylhäältä alaspäin suuntautuvaa lähestymistapaa satunnaisten ja systemaattisten vaikutusten ymmärtämiseksi. Mittausten arvioinnin sijasta sitä käytetään kuitenkin prosessin tuotosten arviointiin. Sillä on yleensä samat edut ja haitat kuin MSA:lla, ja alhaalta ylöspäin suuntautuvaa epävarmuuden arviointimenetelmää voidaan käyttää, jos nämä ovat ongelma.
Aluksi saattaa vaikuttaa siltä, että MSA:n ja SPC:n välillä on perustavanlaatuisia eroja SPC:n hyvin erilaisen terminologian vuoksi. Yleisen syyn aiheuttama vaihtelu (tai vanhemmassa kirjallisuudessa satunnaisen syyn aiheuttama vaihtelu) vastaa kuitenkin tarkkuutta; lyhytaikainen vaihtelu vastaa toistettavuutta; pitkäaikainen vaihtelu vastaa uusittavuutta; ja erityissyistä johtuva vaihtelu (tai vanhemmassa kirjallisuudessa määritettävissä olevan syyn aiheuttama vaihtelu) vastaa harhaa.
SPC painottaa myös paljon enemmän sen varmistamista, että prosessi on ”tilastollisessa hallinnassa”. Laajasti ilmaistuna tämä tarkoittaa, että vaikutukset ovat satunnaisia ja normaalisti jakautuneita ja että kaikki merkittävät systemaattiset vaikutukset on korjattu. Tämä on SPC:n vahvuus, ja se jätetään joskus huomiotta sekä epävarmuuden arvioinnissa että MSA:ssa.
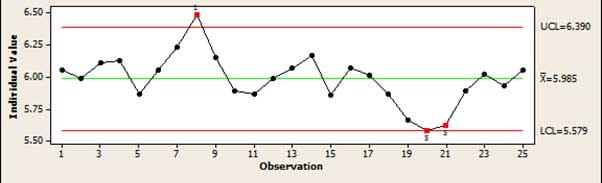
Tärkein SPC:ssä käytetty työkalu, jolla tarkistetaan, että prosessi on ”hallinnassa”, on säätökaavio. Tämä antaa yksinkertaisen graafisen näkymän prosessista, josta voidaan helposti havaita, jos prosessi on ajautumassa tai tuottaa virheitä, joita ei voida selittää tavanomaisilla satunnaisvaihteluilla. Jos esimerkiksi useat pisteet kasvavat tai laskevat, tämä osoittaa, että prosessi on ajautumassa.
Tässä artikkelissa olen yrittänyt antaa laajan yleiskatsauksen suuresta ja monimutkaisesta aiheesta. Olen esitellyt laadun ylläpitämisen perusperiaatteet menemättä kuitenkaan näiden menetelmien soveltamiseen tarvittavaan matematiikkaan.
Pysy kuulolla tulevissa artikkeleissa näistä aiheista.

Tohtori Jody Muelanerin 20-vuotinen insinööriura alkoi konesuunnittelun parissa työskentelemällä kaikenlaisten laitteiden parissa lääkinnällisistä laitteista sahalaitoksiin. Vuodesta 2007 lähtien hän on kehittänyt uudenlaista metrologiaa Bathin yliopistossa työskennellen tiiviisti johtavien ilmailu- ja avaruusalan yritysten kanssa. Tutkimus keskittyy tällä hetkellä tuotantojärjestelmien epävarmuuden mallintamiseen, jossa yhdistyvät SPC:n, MSA:n ja metrologian elementit sekä uudet numeeriset menetelmät. Hän on kiinnostunut myös polkupyörien suunnittelusta. Lisätietoja on hänen verkkosivustollaan.