>Tietäisit ehkä sen, että jos halutaan ratkaista 2. asteen yhtälö, ax²+bx+c = 0, käytämme kvadraattikaavaa.

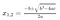
Yhtälöille, joiden aste on 3 ja 4, on olemassa samanlaisia kaavoja, mutta ne puuttuvat mystisesti yhtälöille, joiden aste on 5 tai suurempi. Tarkemmin sanottuna näyttää siltä, että emme voi muodostaa kvintin (asteen 5 yhtälö) tai sitä korkeamman yhtälön ratkaisuja käyttämällä vain yhteen-, vähennys-, kerto- ja jakolaskuja sekä radikaaleja (neliöjuuria, kuutiojuuria jne.). Miksi näin on, mikä numerossa 5 on niin erityistä? Nämä kysymykset askarruttivat nuorta ranskalaista Evariste Galois’ta 1800-luvun alussa, ja yönä ennen kuin hän haavoittui kuolettavasti kaksintaistelussa, hän kirjoitti ylös teorian uudesta matemaattisesta objektista nimeltä ”ryhmä”, joka ratkaisee kysymyksen yllättävän tyylikkäästi.

Näin hän teki sen.

Eriyhtälöiden juurien joukko on eri monimutkainen. Jotkut joukot ovat niin monimutkaisia, että niitä ei voi ilmaista vain yksinkertaisilla kohteilla, kuten radikaaleilla. Mutta miten mittaamme juurten monimutkaisuutta, jos emme voi edes laskea niitä, ja mitä monimutkaisuuden mittaria meidän pitäisi käyttää?

Permutoitavat juuret ja symmetria

Vastaus piilee juurten symmetriassa.

Juurten symmetria saatat kysyä, mitä tekemistä sillä on minkään kanssa? Mitä se edes tarkoittaa?

Piirretään kahden yhtälön juuret ja katsotaan, saammeko siitä tolkkua:

Vasemmalla olevasta yhtälöstä sanotaan, että sen juuret ovat vähemmän symmetrisiä kuin oikealla. Tämä saattaa yllättää, sillä puhekielessä symmetristä käytetään yleensä, jos kohdetta voidaan peilata tai kääntää ilman, että sen ulkonäkö muuttuu. Tässä mielessä vasen kuva näyttää symmetrisemmältä.

Esim: Tähti on symmetrisempi kuin sydän, koska sen heijastamisen lisäksi sitä voi myös kiertää.

Meidän tapauksessamme otamme kuitenkin symmetrioita yleisemmällä tavalla. Emme rajoitu vain heijastuksiin ja rotaatioihin, vaan mikä tahansa funktio, joka muuttaa objektia muuttamatta sen ulkonäköä, on reilu peli. Juurten tapauksessa tämä tarkoittaa, että mikä tahansa funktio, joka vaihtaa (muuttaa) juuria millä tahansa tavalla, on kelvollinen. Enemmän funktioita tarkoittaa symmetrisempää.

Kävi ilmi, että oikeassa tapauksessa on olemassa funktioita kaikkien juurien permutaatiolle missä tahansa kuviteltavissa olevassa järjestyksessä, jopa 5!=120, joten se on erittäin symmetrinen. Mutta vasemmassa tapauksessa, jos vaihdamme r₂↔r₄ käyttäen muunnosta i↔-i, vaihdamme välttämättä myös r₁↔r₅. Tämä rajoittaa meitä, ja siten kaikki ajateltavissa olevat permutaatiot eivät ole mahdollisia. Se on vähemmän symmetrinen.

Juuria permutoivia funktioita kutsutaan ”automorfismeiksi”, ja jos ryhmittelemme nämä automorfismit yhteen, saamme niin sanotun ”ryhmän” (palaan automorfismien ja ryhmien parempiin määritelmiin myöhemmin).

Tämä tarkoittaa, että ryhmä, joka edustaa juurten symmetrioita, on oikeassa tapauksessa suurempi ja monimutkaisempi. Oikeassa tapauksessa ryhmä on itse asiassa niin monimutkainen, että juuria ei voi kuvata radikaalien avulla.

Miten tiedämme, kuinka monimutkainen ryhmä on? Ymmärtääksemme tämän tarvitsemme hieman lisää teoriaa.

Kvintin koko

Katsotaan ensin ryhmän kokoa. Mistä tiedän, että on olemassa kvinttejä, joiden ryhmä on 5! suuri?

Yleinen kvintti näyttää yleensä tältä:

x⁵+ax⁴+bx³+cx²+dx+e=0

Mutta jos lähestymme asiaa ”juurevammin”, voimme sanoa, että se näyttää tältä:

(x-r₁)(x-r₂)(x-r₃)(x-r₄)(x-r₅)=
x⁵-(r₁+r₂+r₂+r₃+r₄+r₅)x⁴+
(r₁r₂+r₁r₃+r₁r₄+r₂r₄+r₃r₄+r₁r₅+r₂r₅+r₃r₅+r₄r₅)x³…- r₁r₂r₃r₂r₃r₄r₅=0

Tämähän tarkoittaa, että ensimmäisessä yhtälössä olevat vakiot a,b,c,d,e korvataan juurten symmetrisellä yhdistelmällä: huomataan, että juurien vaihtaminen keskenään ei vaikuta yhtälöön (kokeile sitä esimerkiksi edellä olevan b:n kohdalla). Tämä pätee kaikenasteisille polynomeille. Koska pystymme vaihtamaan kaikki juuret keskenään, voimme vetää johtopäätöksen, että tämän yleisen kvintin symmetriaryhmä on itse asiassa kaikki permutaatiot, jota kutsutaan myös nimellä S₅ (symmetrinen ryhmä, jonka järjestys on 5).

Kentät ja automorfismit

Nyt laajennamme automorfismien määritelmäämme hiukan, sillä automorfismit ovat muutakin kuin pelkkiä funktioita, jotka permutoivat juuria. Tässä yhteydessä meidän on esiteltävä jotain, jota kutsutaan ”kentiksi”. Miksi haluaisimme tehdä niin, sanotte? Syy on se, että vaikka juurien ja niiden permutaatioiden kanssa työskentely on hauskaa, on hieman helpompaa työskennellä kenttien ja niiden automorfismien kanssa. Kyse on täsmälleen samoista funktioista, älä huoli, vain toisesta tavasta tarkastella niitä.

Jos siis yhtälö on vaikkapa x²-2=0, sen sijaan, että työskentelisimme juurien kanssa, r₁=√2, r₂=-√2, otamme käyttöön kentän Q(√2). Tämä on kaikki rationaaliluvut Q, joihin on lisätty √2. √2:ta kutsutaan ”kentän laajennukseksi”. Se näyttää seuraavalta: a+b√2 a,b∈Q. Jotta voimme kuvata yhtälön juuren, tarvitsemme kentän Q(√2). Jokaiselle kenttälaajennukselle (ja myös muille matemaattisille objekteille) on joukko funktioita σₙ, jotka lähettävät luvun toiselle ainutlaatuiselle luvulle samassa kentässä ja noudattavat ehtoa σ(a+b)=σ(a)+σ(b) ja σ(ab)=σ(a)σ(b). σ on laajennuksen funktio eikä kosketa sen taustalla olevaa kenttää Q. Näitä funktioita kutsutaan automorfismeiksi. Muuten ne myös permuteeraavat juuria. Tämä johtuu siitä, että juurelle r:

r⁵+ar⁴+br³+cr²+dr+e=0⟹
σ(r⁵+ar⁴+br³+cr²+dr+e)=σ(0)⟹
σ(r)⁵+aσ(r)⁴+bσ(r)³+cσ(r)²+dσ(r)+e=0 (koska σ ei kosketa Q:ta (missä a, b, c, d,e elää))

Tämä tarkoittaa, että σ(r) on myös yhtälön ratkaisu. Ja koska:

σ(r₁)-σ(r₂)=σ(r₁)+σ(-1)σ(r₂)=σ(r₁-r₂)≠0

juuret ovat erillisiä, joten niitä on viisi, joiden täytyy olla alkuperäiset viisi. Näin ollen σ:n täytyy permutoida juuret.

Tämä toimii tietysti minkä tahansa asteen yhtälölle.

Siten:

1. Meillä on yhtälömme.
2. Tämässä yhtälössä on kenttä, joka saattaa sisältää muutaman radikaalin laajennuksen
3. Tämässä kenttälaajennuksessa on ryhmä, joka on kokoelma sen kaikista automorfismeista.

Kaksi esimerkkiä 3. asteen yhtälöstä

Yhtälö: x³-x²-2x+2=0

Juuret ovat (1,√2,-√2) (voit todentaa tämän itse liittämällä ne), joten kentän täytyy olla Q(√2)

Kirjoitetaan ylös kaikki mieleen tulevat tavat permutaatioida juuret (e tarkoittaa identiteettipermutaatiota, se ei tee mitään):

(e)
(√2↔-√2)
(1↔√2)
(1↔-√2)
(√2→-√2 ja 1→√2)
(√2↔-√2 ja 1↔-√2)

Kokeillaan yhtä: Olkoon (√2↔-√2) σ₁:

σ₁(√2+-√2)=σ₁(0)=0=σ₁(√2)+σ₁(-√2)
σ₁((√2)(-√2))=σ₁(-2)=-2=σ₁(√2)σ₁(-√2)

Siinä pitkälle. Vielä yksi.

Tulkoon (1↔√2) σ₂:

σ₂(√2+-√2)=σ₂(0)=0 ≠ σ₂(√2)+σ₂(-√2)=1+-√2
σ₂((√2)(-√2))=2 ≠ σ₂(√2)σ₂(-√2)=1(-√2)

Avastaavasti σ₂ ei ole automorfismia, niinpä joudumme hylkäämään. Muut σ törmäävät samanlaisiin ongelmiin, jäljelle jäävät vain e ja σ₁. Tätä kutsutaan sykliseksi ryhmäksi C₂, koska voimme permuteerata vain ympyrässä (tässä tapauksessa hyvin pienessä ympyrässä).

Esimerkki 2

Yhtälö:

Juuret ovat

so kentän on oltava

käyttämällä lyhyyden vuoksi ζ. Tältä se näyttää:

Voi leikkiä juuripermutaatioiden kanssa hieman, ja huomaa pian, että tässä tapauksessa ne ovat kaikki automorfismeja. Automorfismeja on siis 3! eli kaikki juuripermutaatiot, joten ryhmän täytyy olla S₃.

Yllä olevasta kuvasta on hauska huomata myös se, että se näyttää tasasivuiselta kolmiolta ja että automorfismit vastaavat täsmälleen kolmion kiertämistä ja heijastamista. Jos automorfismit vastaavat säännöllisen monikulmion symmetrioita tällä tavalla, ryhmää kutsutaan ”dihedriseksi ryhmäksi”. Tässä tapauksessa D₃. Yleensä kaikkien permutaatioiden ryhmä Sₙ ei ole sama kuin dihedriryhmä Dₙ, mutta tapauksessa n=3 se on.

Ryhmät

Tämä tuntuu olevan hyvä paikka siirtyä hieman pidempään keskusteluun ryhmistä. Ryhmät alkoivat siis juurten permutaatioiden kokoelmina, mutta ne voidaan nähdä myös automorfismien kokoelmina eli symmetristen geometristen kappaleiden rotaatioina ja heijastuksina. Mitä tahansa funktioiden kokoelmaa, joka muuttaa kohdetta siten, että se näyttää samalta, voidaan pitää ryhmänä. Voimme kuitenkin itse asiassa tarkastella itse muunnoksia välittämättä symmetrisestä kohteesta, johon ne vaikuttavat. Aivan samalla tavalla kuin emme vaivaudu omenakasoista, kun teemme aritmeettisia laskutoimituksia, vaan yksinkertaisesti noudatamme sääntöjä, samalla tavalla voimme määritellä joitakin sääntöjä, joita ryhmän muunnokset noudattavat, ja käyttää niitä.

Säännöt ovat jotakuinkin seuraavat:

Jos teemme ensin muunnoksen ja sitten toisen, saamme kolmannen muunnoksen, joka on edelleen ryhmässä. Esimerkiksi ryhmä C₄ on kaikkien niiden pyörähdysten ryhmä, joita voi tehdä neliölle. Jos a kääntyy 90∘, b kääntyy 180∘ ja c kääntyy 270∘, niin a∗b=c. Missä ∗ tarkoittaa, että ensin tehdään b ja sitten a. Tätä kutsutaan yleisesti kertolaskuksi, koska se on (tavallaan) samanlainen kuin lukujen kertominen. Yllä olevan säännön mukaan c:n on oltava ryhmässä. Tätä kutsutaan sulkeutumiseksi.

On oltava identiteettielementti (e), joka ei tee yhtään mitään.

Jokaista elementtiä varten on oltava kyseisen elementin käänteisluku.

Nyt voimme tutkia erilaisten ryhmien ominaisuuksia ilman, että meidän tarvitsee huolehtia juurista tai monikulmioista.

Ryhmien visualisointi

Kaksi hauskaa tapaa visualisoida ryhmiä ovat:

Cayleyn taulukot

Yllä on Cayleyn taulukko tasasivuiselle kolmiolle, D₃-ryhmälle. Siinä on kaikki ryhmän alkuaineet ja mitä alkuaineita saamme, kun kerromme ne. Jos esimerkiksi teemme ensin 120∘:n kierron (r) ja sitten saman kierron uudelleen, saamme 240∘:n kierron rr=r², kuten taulukosta näkyy. Jos teemme 120∘ kierto-käännön rf ja r, saamme tulokseksi pelkän käännöksen. Huomaa, että elementit f ja r eivät vaihtele. Ryhmää, jossa alkuaineet kommutoivat, kutsutaan abeeliseksi ryhmäksi.

Tämä taulukko on silti hyvin symmetrinen, mutta sen ei tarvitse olla niin. Mikä tahansa sääntöjen mukainen alkioiden sekoittuminen on pätevää.

Caylay-graafi

Ylläoleva on D₃ Caylay-graafi. Tässä elementit on esitetty siten, että nähdään, miten elementistä pääsee seuraavaan, jolloin särmät ovat operaatioita. Tässä tapauksessa tarvitaan 120∘ kierto ja kääntäminen, näitä (r ja f) kutsutaan myös ryhmän generaattoreiksi, koska niiden avulla voidaan generoida koko ryhmä identiteettielementistä lähtien.

Ryhmien käyttötarkoitukset

Ryhmät ovat yleensä käyttökelpoisia kaikkialle, missä on symmetria. Esimerkiksi tapettiryhmiä käytetään kuvaamaan symmetrisiä tapetteja. On olemassa taustakuvia, joita voi kääntää 180∘ ja joitakin taustakuvia, joita voi peilata ja joitakin, joissa voi tehdä molempia, ja niin edelleen. Kävi ilmi, että niitä on vain 17, joten se on siisti tapa luokitella taustakuvia.

Yllä olevat taustakuvat kuuluvat molemmat ryhmään nimeltä p6m.

Toinen, yllättävämpi, ryhmien käyttö on fysiikassa. Näyttää siltä, että luonnonlait noudattavat tiettyjä symmetrioita. Jos esimerkiksi muunnetaan Newtonin toinen laki F=ma, 10 minuutin päähän tulevaisuuteen se on edelleen sama. Se, että luonnonlait eivät muutu päivästä toiseen, näyttää osoittavan, että ne ovat symmetrisiä aikamuunnoksen suhteen. Ne eivät myöskään muutu paikasta toiseen, joten myös avaruudessa tapahtuvat muutokset ovat sallittuja. Koska aikaa ja avaruutta on mahdollista muuttaa mielivaltaisen pieninä tai suurina kokonaisuuksina, näitä kuvaavat ryhmät, Lie-ryhmät, sisältävät äärettömän määrän alkioita.

Mielenkiintoisesti käy ilmi, että kaikki nämä symmetriat liittyvät kukin yhteen säilymislakiin. Aikasymmetriaan liittyy energian säilyminen, tilasymmetriaan impulssin säilyminen, kulmasymmetriaan (luonto näyttää samalta kaikista kulmista) kulmamomentin säilyminen ja niin edelleen. Tämän osoitti Emmy Noether yhdistämällä symmetriat pienimmän toiminnan periaatteeseen, joka on luonnonlaki, jonka mukaan luonnolla on taipumus ”kulkea lyhintä tietä”.

Minusta on mielenkiintoista, kuinka suuri osa luonnon monimutkaisuudesta ja näennäisestä kaaoksesta voidaan selittää sellaisilla intuitiivisilla käsitteillä kuin ”luonnonlait eivät muutu päivästä toiseen” ja ”luonnolla on taipumus kulkea lyhintä tietä”.

Takaisin kenttien pariin

Välipuhe loppuu tähän, missä olimme? Aivan, puhuimme x³-3=0:sta ja sen juurista ja kentistä.

Tämän yhtälön kenttä on Q(³√2, ζ) ja olisi luonnollista ajatella, että se näyttää tältä: a+b³√2+cζ, mutta se on väärin. Syy tähän on se, että haluamme kenttämme olevan ”Suljettu”. Toisin sanoen, jos lisäämme tai kerromme kaksi elementtiä kentässä, haluamme niiden pysyvän kentässä. Joten esimerkiksi ³√2 ja ζ ovat molemmat edellä olevassa kentässä, mutta ³√2ζ ei ole.

Alakentät ja alaryhmät

Katsomalla edellä olevia 3. asteen esimerkkejämme, meillä on

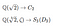
Näyttäisi siltä, että toinen kenttä ja ryhmä ovat monimutkaisempia kuin ensimmäinen kenttä ja ryhmä. Voimme arvata tämän laskemalla termien lukumäärän kenttätapauksessa tai automorfismien lukumäärän ryhmätapauksessa. Mutta pelkkä laskeminen ei näytä todella kuvaavan sitä, mitä kompleksisuus tarkoittaa. Otetaan esimerkiksi ryhmä C₁₂. Siinä on paljon alkioita, mutta se kiertää vain juuria, joten se ei vaikuta kovinkaan monimutkaiselta. Vastaava kenttä on Q(e^π/6). Se sisältää e^π/6,e^2π/6… mutta ei taaskaan kovin monimutkainen.

Huolta siitä, kuinka monimutkainen ryhmä on, tulee olemaan avainasemassa sen ymmärtämisessä, miksi joitain juuria ei voi kuvata pelkillä radikaaleilla, muistakaa.

Saadaksemme paremman tavan arvostaa monimutkaisuutta otamme käyttöön ”alakentän” (Subfield, ”Subfield”) ja ”alaryhmän” (Subgroup, ”Subgroup”) käsitteet. Alikenttä on se, kun poistat osan termeistä, mutta sinulla on edelleen suljettu kenttä. Vastaavasti alaryhmä on se, kun poistat joitakin automorfismeja, mutta sinulla on silti suljettu ryhmä.

Ensimmäisessä tapauksessa Q(√2), ainoa asia, jonka voi tehdä, on poistaa √2 kentässä ja toinen kahdesta automorfismista ryhmässä (emme voi poistaa (e) ja silti saada ryhmää).

Toisen tapauksen Q(³√2, ζ) kohdalla asia muuttuu hieman monimutkaisemmaksi. Voidaan manuaalisesti tislata alakenttä/ryhmä vain poistamalla elementtejä yksi kerrallaan ja katsoa, onko tuloksena oleva kenttä/ryhmä suljettu. Jonkin ajan kuluttua päädytään tähän:

Huomionarvoista on se, että sekä kentässä että ryhmässä on neljä osatekijää. Nyt olisi järkevä arvaus, että alaryhmät sisältävät aina täsmälleen alakenttien automorfismit. Mutta näin ei ole.

Kiinteät kentät

Ei hätää, olemme melkein perillä, se on vain vähän monimutkaisempaa. Nähdäksemme tämän tarkastellaan kenttää Q(⁴√2, i) ja sen alakenttiä.

Kentällä Q(⁴√2, i) on permutaatioryhmä D₄ (sama kuin neliö). Tarkastellaan D₄:tä ja sen alaryhmiä.

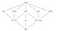
Alaryhmäverkko on tässä kuvassa ylösalaisin, ja D₄ on alareunassa, pääsen siihen pian, mutta tarkastellaan ensin alaryhmien alakenttiä vasten. Q(⁴√2, i):llä on 5 isoa alakenttää ja 3 pientä alakenttää, mutta D₄:llä on vain 3 isoa alakenttää ja 5 pientä alakenttää.

Näyttäisi siltä, että isoja ryhmiä ei ole tarpeeksi, jotta 5 isoa kenttää voitaisiin permutoida. Jos leikkisit alaryhmien ja alakenttien kanssa, tulisit lopulta siihen tulokseen, että alaryhmät eivät itse asiassa permuta alakenttiä, vaan pikemminkin kaikkea, mikä ei ole alakentissä, että ne ”korjaavat” tai eivät koske alakenttiin.

Siten esimerkiksi (f) fiksoi Q(⁴√2) ja (r², f) fiksoi Q(√2).

Miksi asia on näin eikä toisinpäin, kuten ensin arvelimme?

Minulla ei ole intuitiivista tapaa selittää tätä, näen asian niin, että löysimme sen empiirisesti ja nyt voimme yrittää todistaa sen. Todistus menee suurin piirtein näin:

Käsin aaltoileva Galois-teorian perustava lause todistusluonnos

Haluamme osoittaa, että jos käännämme alaryhmähaarukan ylösalaisin, saamme yksi-yhteen vastaavuuden alaryhmähaarukan kanssa, jossa kentät ovat ryhmien kiinteitä kenttiä.

Aluksi haluan huomauttaa, että on järkevää (tavallaan), että asia on näin. Alaryhmässä meillä on kaikki automorfismit, jotka tietysti liikkuvat kaiken muun paitsi Q:n ympärillä (fiksoi Q:n), ja ylhäällä meillä on vain e-automorfismi, joka ei liiku minkään ympärillä (fiksoi kaiken).

Jos aloitamme alaryhmästä ja poistamme muutaman automorfismin, poistetut automorfismit eivät enää liiku pienen osan kentästä ympärillä ja näin ollen fiksoivat tuon osan kentästä. Kun poistamme useampia automorfismeja, yhä suurempi osa kentästä jää koskemattomaksi ja näin ollen saamme suuremman kiinteän kentän.

Jotta olisimme hieman tiukempia, meidän on voitava verrata ryhmän ja kentän kokoa. Ryhmän koko on tietenkin siinä olevien automorfismien lukumäärä. Kentän koko on termien lukumäärä. Nämä kaksi sattuvat olemaan samat, mutta miksi näin on?

Quotiantti

Nyt voisimme tarkastella kvintin S₅-alaryhmäverkkoa ja huomata, että tosiaankin se näyttää aika monimutkaiselta. Mutta sitoaksemme tämän yhteen radikaalien kanssa tarvitsemme tavan analysoida kompleksisuutta ryhmien ja sen alaryhmien välillä. Toisin sanoen: Kuinka paljon monimutkaisempi on D₄ kuin esimerkiksi C₄? Tätä varten otamme käyttöön käsitteen ”Quotientti”. Kvotiivi on periaatteessa ryhmän jako. Miten se toimii?

Tavallisessa jakolaskussa teemme jotakuinkin näin: Jos haluamme jakaa 15 omenaa viidelle henkilölle, ryhmittelemme omenasarjan omenat viiteen yhtä suureen kasaan, ja jokainen kasa vastaa yhtä henkilöä henkilösarjassa. Vastaus kysymykseen 15/5 on 3, yksi kasoista, mikä tahansa kasa kelpaa, koska ne ovat samanarvoisia.

Samankaltainen asia tapahtuu, kun jaamme ryhmiä. Jakaaksemme D₄:n C₄:llä ryhmittelemme D₄:n 8 elementtiä neljään yhtä suureen ryhmään, yksi kutakin C₄:n elementtiä kohden. Miten teemme ryhmistä yhtäläisiä? Eihän elementit ole kaikki samanlaisia omenoita. Ne voivat olla esimerkiksi hyvin erilaisia automorfismeja. No, kvartiilit eivät aina ole mahdollisia juuri tästä syystä. Mutta joskus ryhmä voidaan jakaa ”kosetteihin”. Sanotaan, että jaamme D₄:n neljään yhtä suureen osaan, joissa jokaisessa on 2 elementtiä. Jos olemme onnekkaita, voimme saada 4 elementtikasaa, joissa kahden elementin välinen suhde on sama kaikissa kasoissa. Pystyäksemme tähän alkuperäisen ryhmän on osoitettava suurta itsekohtaista samankaltaisuutta. Nähdäksemme tämän tarkastellaan D₄:n Cayley-graafia.

Kuten nähdään, tässä on itse asiassa korkea itsekohtaisen samankaltaisuuden taso. Vasemmassa yläkulmassa, oikeassa yläkulmassa, vasemmassa alakulmassa ja oikeassa alakulmassa kaikki näyttävät samalta. Tämä on meidän cosetimme.

Siten D₄/C₄ on periaatteessa yksi näistä coseteista, joka on C₂. Näin ollen: D₄/C₄=C₂.

Nyt ottamalla käyttöön kvotientit meillä on itse asiassa käsitys siitä, miten ryhmiä rakennetaan alusta alkaen. Aivan kuten 21 koostuu 3:sta ja 7:stä, myös ryhmät koostuvat alaryhmistä. Ja aivan kuten voimme saada luvun osatekijät jakamalla, 21/7=3, niin voimme saada ryhmän osatekijät ottamalla osamäärän. Koska D₄/C₄=C₂, tämä tarkoittaa, että jos meillä on C₄-ryhmä, meidän on kerrottava se C₂:lla saadaksemme D₄. Koska kenttien ja ryhmien välillä on vastaavuus, tämä vaikuttaa siihen, miten rakennamme kenttiä.

Radikaalit

Kvintin alaryhmät

Nyt, En näytä kuvaa S₅:n ryhmähaarukasta, koska se on liian suuri, mutta sanon pari asiaa sen alaryhmistä. Yksi alaryhmistä on A₅ (vuorotteleva ryhmä), joka on helppo tarkistaa. Jotta pääsemme A₅:stä S₅:hen, tarvitsemme S₅/A₅=C₂. Voimme siis päästä sinne radikaalien avulla, mutta: Yksi A₅:n alaryhmä on (e), mutta A₅/e ei ole syklinen ryhmä. Tämä pätee muuten mille tahansa An:lle, jonka n≥5. Emme siis pääse sinne radikaalien avulla, ja valitettavasti mitään polynomia, jonka aste on≥5, ei voi ratkaista radikaalien avulla.

Ja näin Galois keksi teini-ikäisenä ryhmän käsitteen todistaakseen pitkään avoimena olleen kysymyksen kvintin⁹ ratkaisemattomuudesta.

Kulman leikkaaminen

Yksi hauska bonusfakta, jonka saamme Galois’n teoriaa ympäröivästä koneistosta, tässä tapauksessa kenttien tornilaista, on mukava todiste ongelmasta, joka on askarruttanut ihmiskuntaa antiikin kreikkalaisista lähtien, nimittäin: Mahdottomuus kolmioida kulmaa viivoittimella ja kompassilla. Ilmeisesti kreikkalaiset rakastivat piirtää asioita tällä tavalla ja olivat uteliaita menetelmän rajoituksista.

Yksi esimerkki on pisteen löytäminen kahden muun pisteen keskeltä. Tätä varten asetetaan kompassi kahden pisteen kohdalle ja piirretään ensin ympyrä yhden ja sitten toisen pisteen ympärille. Käytä viivoitinta viivoittimena ja piirrä viiva pisteiden väliin ja sitten pisteiden väliin, joissa ympyrät risteävät. Keskellä on paikka, jossa viivat risteävät.

Mutta miten tämä piirtotapa siirtyy kenttäteoriaan? No, yllä olevan ongelman voi nähdä niin, että vaikkapa meillä on kenttä, jossa on kaksi pistettä, (x₁,y₁) ja (x₂,y₂). Haluaisimme laajentaa kenttää niin, että se sisältää myös keskimmäisen pisteen. Tätä varten etsimme ympyröiden (x-x₁)²+(y-y₁)²=r ja (x-x₂)²+(y-y₂)²=r leikkauspisteet. Saadaan kaksi uutta pistettä (x₃, y₃) ja (x₄,y₄). Niiden välinen suora on y=(y₄-y₃)/(x₄-x₃)x. Kahden ensimmäisen pisteen välinen suora on y=(y₂-y₁)/(x₂-x₁)x. Ratkaise x:n avulla, jotta saat, missä ne risteävät.

Näyttää siltä, että suorakulma- ja kompassikonstruktiot ovat yhtä paljon kuin ykkös- ja kakkosasteen yhtälöiden ratkominen.

Mutta mitä kulman kolmijaottelulla tarkoitetaan?

Kolmiokulman kaava antaa:

Mutta koska suorakulmion ja kompassin käyttäminen oli yhtä kuin yksi- ja kaksiasteisten yhtälöiden ratkominen, ainoat mahdolliset kenttälajin laajentamiset ovat 2:lla yhdelle operaatioille, minkä jälkeen uusilla pisteillä päästäänkin 2:n potensseihin: 4,8,16 jne. mutta ei koskaan 3:een.

Vaikka kulman kolmijaon tekeminen pelkällä viivoittimella ja kompassilla on mahdotonta, se on mahdollista origamin avulla.

Yleisen kvintin ratkaiseminen

On sanottava, että vaikka yleistä kvinttiä ei voi ratkaista radikaaleilla, se voidaan ratkaista ”Jacobin theta-funktiolla”.

1. Galois-teoriaa aloittelijoille: A Historical Perspective. Jörg Bewersdorff
2. http://pi.math.cornell.edu/~kbro…
3. Kenttäautomorfismit
4. https://kconrad.math.uconn.edu/b…
5. https://faculty.math.illinois.ed…
6. Wolfram|Alpha: Making the world’s knowledge computable
7. https://www.wikiwand.com/en/Galois_theory
8. https://www.wikiwand.com/en/%C3%89variste_Galois
9. https://www.youtube.com/watch?v=8qkfW35AqrQ&list=PLwV-9DG53NDxU337smpTwm6sef4x-SCLv&index=36