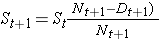Olemme usein kiinnostuneita arvioimaan, onko eloonjäämisessä (tai tapahtuman kumulatiivisessa esiintyvyydessä) eroja eri osallistujaryhmien välillä. Esimerkiksi kliinisessä tutkimuksessa, jossa on eloonjäämistulos, saatamme olla kiinnostuneita vertailemaan eloonjäämistä uutta lääkettä saavien osallistujien välillä verrattuna lumelääkkeeseen (tai vakiohoitoon). Havainnointitutkimuksessa saatamme olla kiinnostuneita vertailemaan eloonjäämistä miesten ja naisten välillä tai sellaisten osallistujien välillä, joilla on ja joilla ei ole tiettyä riskitekijää (esim. verenpainetauti tai diabetes). Käytettävissä on useita testejä, joilla voidaan vertailla eloonjäämistä riippumattomien ryhmien välillä.

Log-rank-testi

Log-rank-testi on suosittu testi, jolla testataan nollahypoteesia siitä, ettei eloonjäämisessä ole eroa kahden tai useamman riippumattoman ryhmän välillä. Testissä verrataan koko eloonjäämiskokemusta ryhmien välillä, ja sitä voidaan ajatella testinä siitä, ovatko eloonjäämiskäyrät identtisiä (päällekkäisiä) vai eivät. Eloonjäämiskäyrät arvioidaan kullekin ryhmälle erikseen Kaplan-Meierin menetelmällä ja niitä verrataan tilastollisesti log-rank-testillä. On tärkeää huomata, että log-rank-testin tilastosta on olemassa useita muunnelmia, jotka on toteutettu eri tilastollisissa laskentapaketeissa (esim. SAS, R 4,6). Esittelemme tässä yhden version, joka liittyy läheisesti khiin neliö -testistatistiikkaan ja jossa verrataan havaittujen ja odotettujen tapahtumien lukumäärää kullakin ajanhetkellä seurantajakson aikana.

Esimerkki:

Pientä kliinistä tutkimusta tehdään kahden yhdistelmähoidon vertailemiseksi potilailla, joilla on pitkälle edennyt mahasyöpä. Kaksikymmentä osallistujaa, joilla on vaiheessa IV oleva mahasyöpä ja jotka suostuvat osallistumaan tutkimukseen, satunnaistetaan saamaan kemoterapiaa ennen leikkausta tai kemoterapiaa leikkauksen jälkeen. Ensisijainen päätetapahtuma on kuolema, ja osallistujia seurataan enintään 48 kuukauden (4 vuoden) ajan tutkimukseen osallistumisen jälkeen. Tutkimuksen kumpaankin haaraan osallistuneiden kokemukset on esitetty alla.

Kemoterapia ennen leikkausta			Kemoterapia leikkauksen jälkeen
Kuukausi. Kuolema	Viimeisen yhteydenoton kuukausi		Viimeisen yhteydenoton kuukausi	Viimeisen yhteydenoton kuukausi
8	8		33	48
12	32		28	48
26	20		41	25
14	40			37
21				48
27				25
				43

Kuusi osallistujaa sytostaattihoitoa ennen leikkausta -ryhmässä kuoli seurannan aikana-verrattuna kolmeen osallistujaan kemoterapiaa leikkauksen jälkeen -ryhmässä. Muita osallistujia kussakin ryhmässä seurataan vaihtelevan määrän kuukausia, joitakin tutkimuksen loppuun 48 kuukauteen asti (kemoterapiaa leikkauksen jälkeen -ryhmässä). Edellä kuvattuja menettelyjä käyttäen laadimme ensin elinaikataulukot kullekin hoitoryhmälle Kaplan-Meierin menetelmää käyttäen.

Elinaikataulukko ryhmälle, joka sai kemoterapiaa ennen leikkausta

Aika, Months	Number at Risk Nt	Number of Deaths Dt	Lukumäärä sensuroitu Ct	Eloonjäämistodennäköisyys
0	10			1
8	10	1	1	0.900
12	8	1		0.788
14	7	1		0.675
20	6		1	0.675
21	5	1		0.540
26	4	1		0.405
27	3	1		0.270
32	2		1	0.270
40	1		1	0.270

Leikkauksen jälkeen kemoterapiaa saavan ryhmän elinaikataulukko

Aika, Months	Number at Risk Nt	Number of Deaths Dt	Lukumäärä sensuroitu Ct	Eloonjäämistodennäköisyys
0	10			1
25	10		2	1.000
28	8	1		0.875
33	7	1		0.750
37	6		1	0.750
41	5	1		0.600
43	4		1	0.600
48	3		3	0.600

Kahdesta eloonjäämiskäyrästöstä on esitetty alla.

Eloonjääminen kussakin hoitoryhmässä

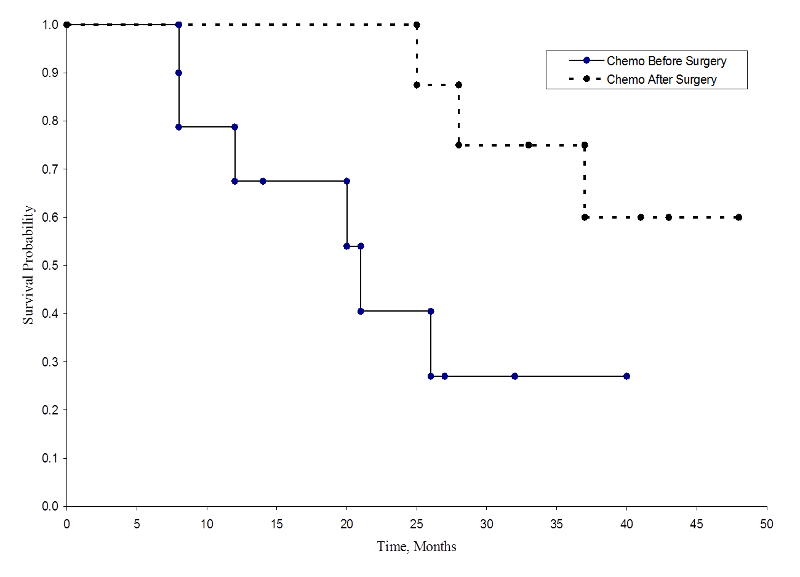
Solunsalpaajahoitoa leikkauksen jälkeen -ryhmän eloonjäämistodennäköisyydet ovat suuremmat kuin solunsalpaajahoitoa ennen leikkausta -ryhmän eloonjäämistodennäköisyydet, mikä viittaa eloonjäämishyötyyn. Nämä eloonjäämiskäyrät on kuitenkin arvioitu pienistä otoksista. Ryhmien välisen selviytymisen vertailemiseksi voidaan käyttää log-rank-testiä. Nollahypoteesina on, että näiden kahden ryhmän välillä ei ole eroa eloonjäämisessä tai että populaatioiden välillä ei ole eroa kuoleman todennäköisyydessä missään vaiheessa. Log-rank-testi on ei-parametrinen testi, eikä se tee oletuksia eloonjäämisjakaumista. Pohjimmiltaan log-rank-testissä verrataan havaittua tapahtumien lukumäärää kussakin ryhmässä siihen, mitä olisi odotettavissa, jos nollahypoteesi olisi tosi (ts, jos eloonjäämiskäyrät olisivat identtiset).

H0: Kaksi eloonjäämiskäyrää ovat identtiset (tai S1t = S2t) vs. H1: Kaksi eloonjäämiskäyrää eivät ole identtiset (tai S1t ≠ S2t, millä tahansa ajankohdalla t) (α=0,05).

Log-rank-statistiikka jakaantuu likimääräisesti khiin neliö -testistatistiksi. Testistatistiikasta on olemassa useita muotoja, ja ne vaihtelevat sen suhteen, miten ne lasketaan. Käytämme seuraavaa:

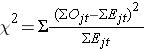
jossa ΣOjt edustaa j:nnen ryhmän havaittujen tapahtumien lukumäärän summaa ajassa (esim. j=1,2) ja ΣEjt edustaa j:nnen ryhmän odotettujen tapahtumien lukumäärän summaa ajassa.

Havaittujen ja odotettujen tapahtumien lukumäärien summat lasketaan kullekin tapahtuma-ajankohdalle ja summataan kullekin vertailuryhmälle. Log rank -tilaston vapausasteet ovat yhtä suuret kuin k-1, missä k edustaa vertailuryhmien lukumäärää. Tässä esimerkissä k=2, joten testistatistiikalla on 1 vapausaste.

Testistatistiikan laskemiseksi tarvitsemme havaitun ja odotetun tapahtumamäärän kullakin tapahtuma-ajankohdalla. Havaitut tapahtumamäärät ovat otoksesta ja odotetut tapahtumamäärät lasketaan olettaen, että nollahypoteesi on tosi (eli että eloonjäämiskäyrät ovat identtiset).

Tapahtumien odotettujen lukumäärien tuottamiseksi järjestämme aineiston elossaolotaulukkoon, jossa rivit edustavat kutakin tapahtuma-aikaa riippumatta siitä, missä ryhmässä tapahtuma tapahtui. Pidämme myös kirjaa ryhmäjakautumisesta. Arvioimme sitten kullakin ajankohdalla tapahtuvien tapahtumien osuuden (Ot/Nt) käyttäen molempien ryhmien tietoja yhdistettynä olettaen, että eloonjäämisessä ei ole eroa (eli olettaen, että nollahypoteesi on tosi). Kerromme nämä estimaatit riskissä olevien osallistujien lukumäärällä kyseisenä ajankohtana kussakin vertailuryhmässä (N1t ja N2t ryhmille 1 ja 2).

Kohtaisesti laskemme kullekin tapahtuma-ajankohdalle t riskissä olevien osallistujien lukumäärän kussakin ryhmässä, Njt (esim. j tarkoittaa ryhmää, j=1, 2) ja tapahtumien (kuolemantapausten) lukumäärän (Ojt), Ojt ,kussakin ryhmässä. Alla oleva taulukko sisältää tiedot, joita tarvitaan log-rank-testin suorittamiseen edellä esitettyjen eloonjäämiskäyrien vertailemiseksi. Ryhmä 1 edustaa kemoterapiaa ennen leikkausta käyttävää ryhmää ja ryhmä 2 kemoterapiaa leikkauksen jälkeen käyttävää ryhmää.

Data for Log Rank Test to Compare Survival Curves

Aika, Months	Riskiluku ryhmässä 1 N1t	Riskiluku ryhmässä 2 N2t	Tapahtumien (kuolemantapausten) lukumäärä ryhmässä 1 O1t	Luku. of Events (Deaths) in Group 2 O2t
8	10	10	1	0
12	8	10	1	0
14	7	10	1	0
21	5	10	1	0
26	4	8	1	0
27	3	8	1	0
28	2	8	0	1
33	1	7	0	1
41	0	5	0	1

Seuraavaksi laskemme yhteen riskissä olevien määrän, Nt = N1t+N2t, kullakin tapahtuma-ajankohdalla ja havaittujen tapahtumien (kuolemantapausten) määrän, Ot = O1t+O2t, kullakin tapahtuma-ajankohdalla. Tämän jälkeen lasketaan tapahtumien odotettu lukumäärä kussakin ryhmässä. Tapahtumien odotettu lukumäärä lasketaan kullakin tapahtuma-ajankohdalla seuraavasti:

E1t = N1t*(Ot/Nt) ryhmälle 1 ja E2t = N2t*(Ot/Nt) ryhmälle 2. Laskelmat on esitetty alla olevassa taulukossa.

Tapahtumien odotetut lukumäärät kussakin ryhmässä

Aika, Months	Riskissä olevien määrä ryhmässä 1 N1t	Riskissä olevien määrä ryhmässä 2 N2t		Riskissä olevien määrä yhteensä Nt	Tapahtumien lukumäärä ryhmässä 1 O1t	Tapahtumien lukumäärä ryhmässä 2 O2t	Tapahtumien kokonaismäärä Ot	Tapahtumien odotettu lukumäärä Ryhmässä 1 E1t = N1t*(Ot/Nt)	Tapahtumien odotettu lukumäärä Ryhmässä 2 E2t = N2t*(Ot/Nt)
8	10	10	20	1	0	1	0.500	0.500
12	8	10	18	1	0	1	0.444	0.556
14	7	10	17	1	0	1	0.412	0.588
21	5	10	15	1	0	1	0.333	0.667
26	4	8	12	1	0	1	0.333	0.667
27	3	8	11	1	0	1	0.273	0.727
28	2	8	10	0	1	1	0.200	0.800
33	1	7	8	0	1	1	0.125	0.875
41	0	5	5	0	1	1	0.000	1.000

Seuraavaksi laskemme yhteen kunkin ryhmän havaitut tapahtumamäärät (∑O1t ja ΣO2t) ja kunkin ryhmän odotetut tapahtumamäärät (ΣE1t ja ΣE2t) ajan suhteen. Nämä on esitetty seuraavan taulukon alimmalla rivillä.

Havaittujen ja odotettujen tapahtumien kokonaismäärät kussakin ryhmässä

Aika, Months	Riskissä olevien lukumäärä ryhmässä 1 N1t	Riskissä olevien lukumäärä ryhmässä 2 N2t	Riskissä olevien lukumäärä yhteensä Nt	Tapahtumien lukumäärä ryhmässä 1 O1t	Tapahtumien lukumäärä ryhmässä 2 O2t	Tapahtumien kokonaismäärä Ot	Tapahtumien odotettu lukumäärä Ryhmässä 1 E1t = N1t*(Ot/Nt)	Tapahtumien odotettu lukumäärä Ryhmässä 2 E2t = N2t*(Ot/Nt)
8	10	10	20	1	0	1	0.500	0.500
12	8	10	18	1	0	1	0.444	0.556
14	7	10	17	1	0	1	0.412	0.588
21	5	10	15	1	0	1	0.333	0.667
26	4	8	12	1	0	1	0.333	0.667
27	3	8	11	1	0	1	0.273	0.727
28	2	8	10	0	1	1	0.200	0.800
33	1	7	8	0	1	1	0.125	0.875
41	0	5	5	0	1	1	0.000	1.000
				6	3		2.620	6.380

Voimme nyt laskea testistatistiikan:

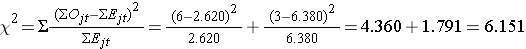
Testistatistiikka jakaantuu approksimatiivisesti khiin neliönä 1 vapausasteella. Näin ollen testin kriittinen arvo löytyy taulukosta Χ2-jakauman kriittiset arvot.

Tälle testille päätössääntö on hylätä H0, jos Χ2 > 3.84. Havaitsemme Χ2 = 6,151, joka ylittää kriittisen arvon 3,84. Näin ollen hylkäämme H0:n. Meillä on merkitsevää näyttöä, α=0,05, joka osoittaa, että nämä kaksi eloonjäämiskäyrää ovat erilaisia.

Esimerkki:

Tutkija haluaa arvioida lyhyen intervention tehokkuutta alkoholinkäytön ehkäisemiseksi raskauden aikana. Raskaana olevat naiset, joilla on aiemmin ollut runsasta alkoholinkäyttöä, rekrytoidaan tutkimukseen ja satunnaistetaan saamaan joko lyhyt interventio, jossa keskitytään alkoholista pidättäytymiseen, tai tavanomainen raskaudenaikainen hoito. Kiinnostava lopputulos on alkoholinkäytön uusiutuminen. Naiset rekrytoidaan tutkimukseen noin 18 raskausviikolla, ja heitä seurataan koko raskauden ajan synnytykseen asti (noin 39 raskausviikolla). Alla on esitetty tiedot, joista käy ilmi, aloittavatko naiset uudelleen juomisen, ja jos aloittavat, milloin he joivat ensimmäisen kerran satunnaistamisesta kuluneiden viikkojen lukumääränä mitattuna. Niiden naisten osalta, jotka eivät palaa takaisin, kirjataan niiden viikkojen lukumäärä satunnaistamisesta, jolloin he ovat olleet alkoholittomia.

Tavanomainen raskaudenaikainen hoito			Lyhyt interventio
Relapse	Ei relapse		Relapse	Ei relapse	Ei relapse
19	20		16	21
6	19		21	15
5	17		7	18
4	14			18
					5

Kiinnostavana kysymyksenä on se, onko tavanomaiseen synnytystä edeltävään hoitoon määrätyillä ja lyhytinterventioon määrätyillä naisilla eroa ajassa, joka kuluu ennen uusiutumista.

• Vaihe 1.

Aseta hypoteesit ja määrittele merkitsevyystaso.

H0: Ryhmien välinen relapsivapaa aika on identtinen vs.

H1: Ryhmien välinen relapsivapaa aika ei ole identtinen (α=0.05)

• Vaihe 2.

Valitse sopiva testitilasto.

Log-rank-testin testistatistiikka on

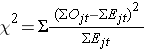
• Vaihe 3.

Päätöksentekosäännön asettaminen.

Testistatistiikka noudattaa khiin neliö -jakaumaa, joten löydämme kriittisen arvon taulukosta kriittisten arvojen taulukosta Χ2-jakaumalle), kun df=k-1=2-1=1 ja α=0.05. Kriittinen arvo on 3,84 ja päätössääntö on hylätä H0, jos Χ2 > 3,84.

• Vaihe 4.

Testistatistiikan laskeminen.

Testistatistiikan laskemiseksi järjestämme aineiston tapahtuma- (relapsi-) ajankohtien mukaan ja määrittelemme riskiryhmään kuuluvien naisten lukumäärät kussakin hoitoryhmässä ja relapsien lukumäärän kullakin havaitulla relapsi-ajankohdalla. Seuraavassa taulukossa ryhmä 1 edustaa naisia, jotka saavat tavanomaista raskaudenaikaista hoitoa, ja ryhmä 2 edustaa naisia, jotka saavat lyhytinterventiota.

Aika, Viikkoja	Riskissä olevien määrä – Ryhmä 1 N1t	Riskissä olevien määrä – Ryhmä 2 N2t	Riskissä olevien määrä – Ryhmä 1 O1t	Riskissä olevien määrä – Ryhmä 1 O1t	Riskissä olevien määrä – Ryhmä 1 O1t	. Ryhmä 2 O2t
4	8	8	8	1	0
5	7	8	1	0
6	6	7	1	0
7	5	7	0	1
16	4	5	0	1
19	3	2	1	0
21	0	2	0	1

Seuraavaksi laskemme yhteen riskiluvun, 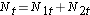kullakin tapahtuma-ajankohdalla, havaittujen tapahtumien (relapsien) lukumäärän 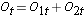kullakin tapahtuma-ajankohdalla ja määrittelemme odotetun relapsien lukumäärän kussakin ryhmässä kullakin tapahtuma-ajankohdalla käyttäen 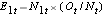ja .

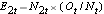Summataan sitten havaitut tapahtumien lukumäärät kussakin ryhmässä (ΣO1t ja ΣO2t) ja odotetut tapahtumien lukumäärät kussakin ryhmässä (ΣE1t ja ΣE2t) ajan kuluessa. Tämän esimerkin tietoja koskevat laskelmat on esitetty alla.

Aika, Viikkoja	Riskiryhmän 1 lukumäärä N1t	Riskiryhmän 2 lukumäärä N2t	Riskiryhmän 2 lukumäärä N2t	Riskiryhmän 1 lukumäärä N1t	. Relapsien määrä Ryhmä 1 O1t	Relapsien määrä Ryhmä 2 O2t	Kokonaisluku Relapsien määrä . Ot	Relapsien odotettu määrä ryhmässä 1	Relapsien odotettu määrä ryhmässä 2
4	8	8	16	1	0	1	0.500	0.500
5	7	8	15	1	0	1	0.467	0.533
6	6	7	13	1	0	1	0.462	0.538
7	5	7	12	0	1	1	0.417	0.583
16	4	5	9	0	1	1	0.444	0.556
19	3	2	5	1	0	1	0.600	0.400
21	0	2	2	0	1	1	0.000	1.000
				4	3		2.890	4.110

Laskemme nyt testistatistiikan:

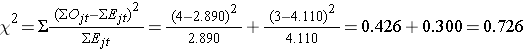
• Vaihe 5.

Tulos. Ei hylätä H0, koska 0,726 < 3,84. Meillä ei ole tilastollisesti merkitsevää näyttöä α=0,05:llä, joka osoittaisi, että relapsiin kulunut aika eroaa ryhmien välillä.

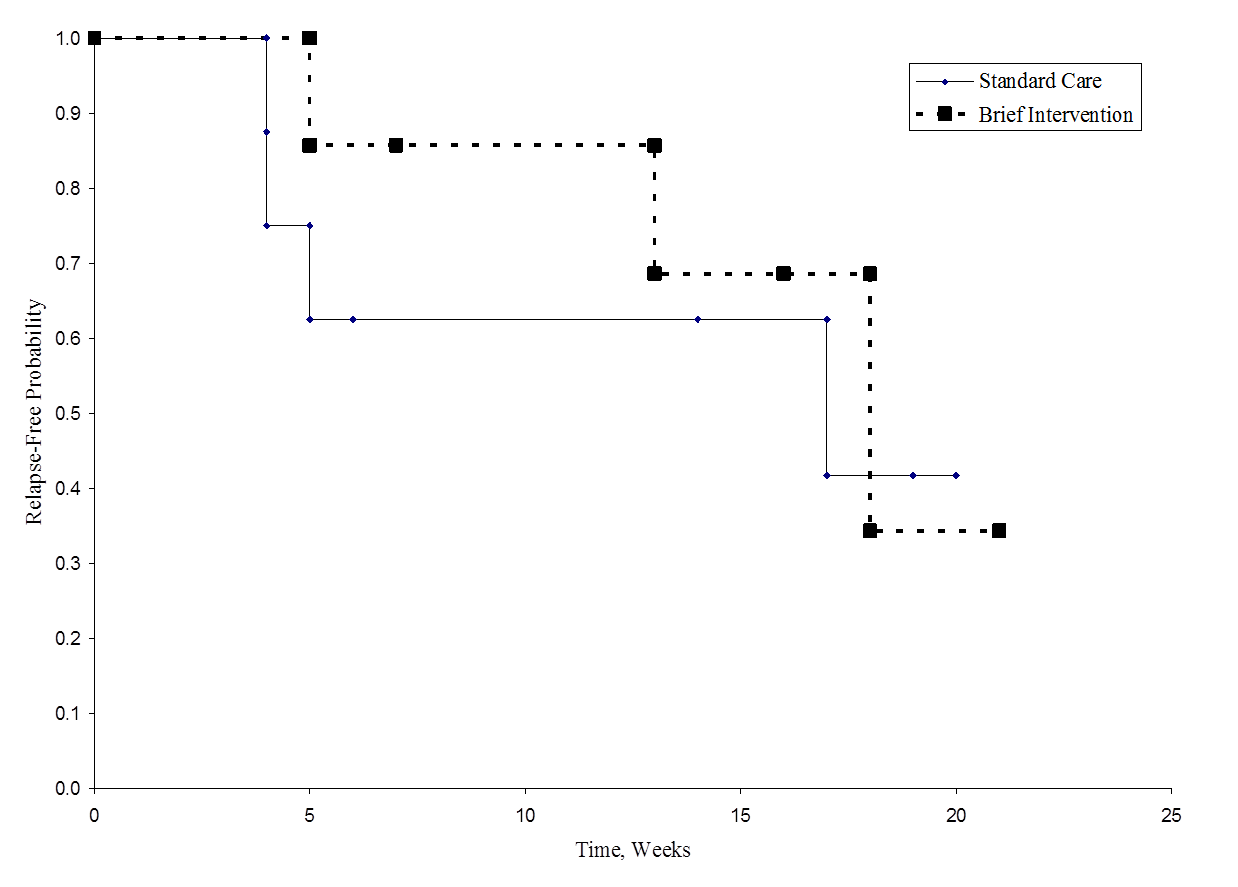
Alla olevassa kuvassa on esitetty elossaoloaika (relapsivapaa aika) kussakin ryhmässä. Huomaa, että eloonjäämiskäyrät eivät juuri eroa toisistaan, mikä on yhdenmukaista hypoteesin testauksessa saatujen ei-merkitsevien tulosten kanssa.

Relapse-vapaa aika kussakin ryhmässä

Kuten todettiin, log-rank-statistiikasta on olemassa useita variaatioita. Joissakin tilastollisissa laskentapaketeissa käytetään kahden riippumattoman ryhmän vertailuun seuraavaa log-rank-testin testistatistiikkaa:

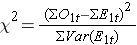
jossa ΣO1t on havaittujen tapahtumien lukumäärän summa ryhmässä 1 ja ΣE1t on odotettujen tapahtumien lukumäärän summa ryhmässä 1 kaikista tapahtuma-ajankohdista. Nimittäjä on tapahtumien odotettujen lukumäärien varianssien summa kullakin tapahtuma-ajankohdalla, joka lasketaan seuraavasti:

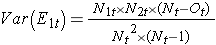
On olemassa muitakin versioita log rank -tilastosta sekä muita testejä, joilla voidaan verrata eloonjäämisfunktioita riippumattomien ryhmien välillä.7-9. Suosittu testi on esimerkiksi modifioitu Wilcoxonin testi, joka on herkkä suuremmille eroille vaaratekijöissä varhaisemmassa kuin myöhemmässä seurannassa.10

palaa alkuun | edellinen sivu | seuraava sivu