Disclaimer 1 : Tämä artikkeli on vain johdatus MFCC-ominaisuuksiin ja se on tarkoitettu niille, jotka tarvitsevat helppoa ja nopeaa ymmärrystä siitä. Yksityiskohtaista matematiikkaa ja koukeroita ei käsitellä.
En ole koskaan itse työskennellyt puheenkäsittelyn parissa, ja kun törmäsin sanaan ”MFCC” (jota kollegat käyttävät melko usein), minulle jäi puutteellinen käsitys siitä, että se on nimi, joka on annettu tietynlaiselle äänisignaaleista poimitulle ”piirteelle” (samaan tapaan kuin särmät muodostavat eräänlaisen kuvista poimitun piirteen).


Minulta kesti melko paljon lukemista useista eri lähteistä ymmärtää aloittelijan käsitys siitä, mitä MFCC-piirteet ovat. Niinpä päätin auttaa apua tarvitsevia kanssaihmisiäni kokoamalla keräämäni tiedot helposti ymmärrettävään muotoon.
Aloitetaan laajentamalla lyhennettä MFCC – Mel Frequency Cepstral Co-efficients.
Oletko koskaan ennen kuullut sanaa cepstral? Todennäköisesti et. Se on spektraali spekseillä päinvastoin! Miksi kuitenkin? Hyvin yksinkertaisen ymmärryksen vuoksi cepstrum on tieto spektrikaistojen muutosnopeudesta. Tavanomaisessa aikasignaalien analyysissä kaikki jaksolliset komponentit (esim. kaiku) näkyvät terävinä piikkeinä vastaavassa taajuusspektrissä (eli Fourier-spektrissä). Tämä saadaan soveltamalla Fourier-muunnosta aikasignaaliin). Tämä näkyy seuraavasta kuvasta:

Valitsemalla tämän Fourier-spektrin suuruuden logaritmin ja ottamalla tämän logaritmin spektri kosinimuunnoksella (tiedän, että se kuulostaa mutkikkaalta, mutta kärsivällisyyttä, olkaa hyvä ja kestäkää kanssani!) havaitaan piikkiä siellä, missä alkuperäisessä aikasignaalissa on jaksollinen elementti. Koska sovellamme muunnosta itse taajuusspektriin, tuloksena saatava spektri ei ole taajuus- eikä aika-alueella, ja siksi Bogert et al. päättivät kutsua sitä quefrency-alueeksi. Ja tämä aikasignaalin spektrin login spektri nimettiin cepstrumiksi (ta-da!).
Oheinen kuva on yhteenveto edellä selostetuista vaiheista.

Cepstrum otettiin ensimmäisen kerran käyttöön, kun haluttiin karakterisoida maanjäristysten seurauksena syntyviä seismisiä kaikuja.
Puheääni (pitch) on puheäänisignaalin ominaispiirteisiin kuuluva ominaisuus, ja sitä mitataan signaaleiden taajuuksina. Mel-asteikko on asteikko, joka suhteuttaa äänen koetun taajuuden todelliseen mitattuun taajuuteen. Se skaalaa taajuuden vastaamaan paremmin sitä, mitä ihmiskorva kuulee (ihminen tunnistaa paremmin puheen pienet muutokset matalammilla taajuuksilla). Tämä asteikko on johdettu ihmisillä tehtyjen kokeiden perusteella. Annan sinulle intuitiivisen selityksen siitä, mitä mel-asteikko kuvaa.
Ihmisen kuuloalue on 20 Hz – 20 kHz. Kuvittele sävel 300 Hz:n taajuudella. Tämä kuulostaisi jotakuinkin lankapuhelimen tavalliselta soittoääneltä. Kuvittele nyt sävel 400 Hz:n taajuudella (hieman korkeampi valintaääni). Vertaa nyt näiden kahden äänen välistä etäisyyttä riippumatta siitä, miten aivosi sen havaitsevat. Kuvittele nyt 900 Hz:n signaali (samanlainen kuin mikrofonin palauteääni) ja 1 kHz:n ääni. Näiden kahden äänen välinen etäisyys voi tuntua suuremmalta kuin kahden ensimmäisen äänen välillä, vaikka todellinen ero on sama (100 Hz). Mel-asteikko pyrkii vangitsemaan tällaiset erot. Hertzissä (f) mitattu taajuus voidaan muuntaa Mel-asteikolle seuraavan kaavan avulla :
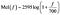
Jokainen ihmisen tuottama ääni määräytyy ääntöväylän muodon (mukaan lukien kielen, hampaiden yms.) mukaan. Jos tämä muoto voidaan määrittää oikein, mikä tahansa tuotettu ääni voidaan esittää tarkasti. Puhesignaalin ajallinen tehospektri edustaa äänirakennetta, ja MFCC (joka ei ole muuta kuin Mel-taajuusspektrin muodostavia kertoimia) edustaa tarkasti tätä kuorta. Seuraava lohkokaavio on vaiheittainen yhteenveto siitä, miten päädyimme MFCC:iin:
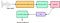
Tässä suodatinpankki viittaa mel-suodattimiin (mel-asteikolle peittäviin suodattimiin), ja Cepstral Coefficients (kefstraalikertoimet) ovat ei mitään muuta kuin mel-frekvenssejä.
TL; DR – MFCC-ominaisuudet edustavat foneemeja (erillisiä ääniyksiköitä), koska niissä ilmenee äänihuulten muoto (joka vastaa äänenmuodostuksesta).
Disclaimer 2 : Kaikki kuvat ovat Google imagesista.