En el tutorial de modelos lineales generalizados, aprendimos sobre varios GLM como la regresión lineal, la regresión logística, etc.. En este tutorial de la serie de tutoriales de R de TechVidvan, vamos a ver la regresión lineal en R en detalle. Aprenderemos qué es la regresión lineal en R y cómo implementarla en R. Veremos el método de estimación de mínimos cuadrados y también aprenderemos a comprobar la precisión del modelo.
Así que, sin más preámbulos, ¡comencemos!
Manteniéndote al día con las últimas tendencias tecnológicas, únete a TechVidvan en Telegram
Regresión lineal en R
La regresión lineal en R es un método utilizado para predecir el valor de una variable utilizando el valor(es) de una o más variables predictoras de entrada. El objetivo de la regresión lineal es establecer una relación lineal entre la variable de salida deseada y los predictores de entrada.
Modelar una variable continua Y como una función de una o más variables predictoras de entrada Xi, de modo que la función pueda utilizarse para predecir el valor de Y cuando sólo se conocen los valores de Xi. La forma general de dicha relación lineal es:
Y=?0+?1 X
Aquí, ?0 es la intercepción
y ?1 es la pendiente.
Tipos de regresión lineal en R
Hay dos tipos de regresión lineal en R:
- Regresión lineal simple
- Regresión lineal múltiple
Veamos uno por uno.
Regresión lineal simple en R
La regresión lineal simple tiene como objetivo encontrar una relación lineal entre dos variables continuas. Es importante tener en cuenta que la relación es de naturaleza estadística y no determinista.
Una relación determinista es aquella en la que el valor de una variable se puede encontrar con precisión utilizando el valor de la otra variable. Un ejemplo de relación determinista es la que existe entre los kilómetros y las millas. Utilizando el valor del kilómetro, podemos encontrar con precisión la distancia en millas. Una relación estadística no es exacta y siempre tiene un error de predicción. Por ejemplo, dados suficientes datos, podemos encontrar una relación entre la altura y el peso de una persona, pero siempre habrá un margen de error y existirán casos excepcionales.
La idea detrás de la regresión lineal simple es encontrar una línea que se ajuste mejor a los valores dados de ambas variables. Esta línea puede entonces ayudarnos a encontrar los valores de la variable dependiente cuando faltan.
Estudiemos esto con la ayuda de un ejemplo. Tenemos un conjunto de datos que consiste en las alturas y pesos de 500 personas. Nuestro objetivo aquí es construir un modelo de regresión lineal que formule la relación entre la altura y el peso, de manera que cuando demos la altura(Y) como entrada al modelo, éste pueda darnos el peso(X) a cambio con un margen o error mínimo.
Y=b0+b1X
Los valores de b0 y b1 deben elegirse de manera que minimicen el margen de error. La métrica del error puede utilizarse para medir la precisión del modelo.
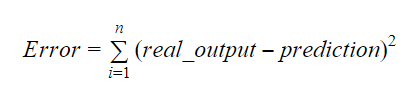
Podemos calcular la pendiente o el coeficiente como: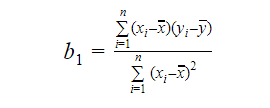
El valor de b1 nos da una idea de la naturaleza de la relación entre la variable dependiente y la independiente.
- Si b1 > 0, entonces las variables tienen una relación positiva, es decir el aumento de x resultará en un aumento de y.
- Si b1 < 0, entonces las variables tienen una relación negativa es decir, el aumento de x resultará en una disminución de y.
El valor de b0 o intercepción puede calcularse como sigue: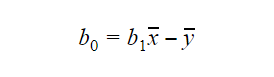 El valor de b0 también puede dar mucha información sobre el modelo y viceversa.
El valor de b0 también puede dar mucha información sobre el modelo y viceversa.
Si el modelo no incluye x=0, entonces la predicción no tiene sentido sin b1. Para que el modelo sólo tenga b0 y no b1 en algún punto, el valor de x tiene que ser 0 en ese punto. En casos como el de la altura, x no puede ser 0 y la altura de una persona no puede ser 0. Por lo tanto, dicho modelo no tiene sentido con sólo b0.
Si falta el término b0 entonces el modelo pasará por el origen, lo que significará que la predicción y el coeficiente de regresión (pendiente) estarán sesgados.
Regresión lineal múltiple en R
La regresión lineal múltiple es una extensión de la regresión lineal simple. En la regresión lineal múltiple, nuestro objetivo es crear un modelo lineal que pueda predecir el valor de la variable objetivo utilizando los valores de múltiples variables predictoras. La forma general de dicha función es la siguiente:
Y=b0+b1X1+b2X2+…+bnXn
Evaluación de la precisión del modelo
Existen varios métodos para evaluar la calidad y la precisión del modelo. Veamos algunos de estos métodos uno por uno.
R-cuadrado
La verdadera información de los datos es la varianza que transmiten. El R-cuadrado nos indica la proporción de la variación de la variable objetivo (y) explicada por el modelo. Podemos encontrar la medida R-cuadrado de un modelo utilizando la siguiente fórmula: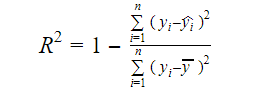
Donde,
- yi es el valor ajustado de y para la observación i
- y es la media de Y.
Un valor menor de R-cuadrado significa una menor precisión del modelo. Sin embargo, la medida de R-cuadrado no es necesariamente un factor decisivo final.
R-cuadrado ajustado
A medida que aumenta el número de variables en el modelo, el valor de R-cuadrado también aumenta. Esto también provoca errores en la variación explicada por las nuevas variables añadidas. Por lo tanto, ajustamos la fórmula de R cuadrado para múltiples variables.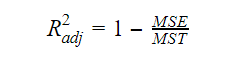 Aquí, el MSE significa Error Estándar Medio que es:
Aquí, el MSE significa Error Estándar Medio que es:
Y MST significa Total Estándar Medio que viene dado por: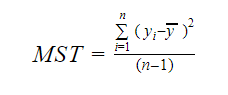
Donde, n es el número de observaciones y q es el número de coeficientes.
La relación entre R-cuadrado y R-cuadrado ajustado es: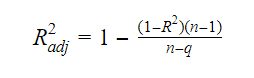
Error estándar y estadístico F
El error estándar y el estadístico F son medidas de la calidad del ajuste de un modelo. Las fórmulas para el error estándar y el estadístico F son:
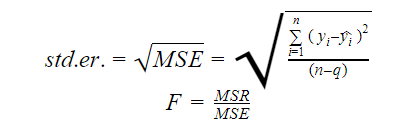
Donde MSR significa Regresión cuadrática media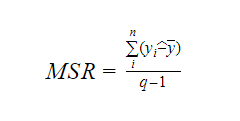
AIC y BIC
El Criterio de Información de Akaike y el Criterio de Información Bayesiano son medidas de la calidad del ajuste de los modelos estadísticos. También pueden utilizarse como criterios para la selección de un modelo.
AIC=(-2)*ln(L)+2*k
BIC=(-2)*ln(L)+k*ln(n)
Donde,
- L es la función de verosimilitud,
- k es el número de parámetros del modelo,
- n es el tamaño de la muestra.
Función lm en R
La función lm() de R ajusta modelos lineales. Puede llevar a cabo la regresión y el análisis de la varianza y la covarianza. La sintaxis de la función lm es la siguiente:
lm(formula, data, subset, weights, na.action,method = "qr", model = TRUE, x = FALSE, y = FALSE, qr = TRUE,singular.ok = TRUE, offset, …)
Donde,
- fórmula es un objeto de clase «fórmula» y es una representación simbólica del modelo a ajustar,
- datos es el marco de datos o lista que contiene las variables de la fórmula(datos es un argumento opcional. Si falta, la función recoge las variables del entorno),
- subset es un vector opcional que contiene un subconjunto de observaciones que se van a utilizar en el proceso de ajuste,
- weights es un vector opcional que especifica los pesos que se van a utilizar en el proceso de ajuste,
- na.action es una función que muestra lo que debe ocurrir cuando se encuentran NA’s en los datos,
- method significa el método para ajustar el modelo,
- model, x, y, y qr son lógicos que controlan si los valores correspondientes deben ser devueltos con la salida o no. Estos valores son:
- modelo: el marco del modelo
- x: la matriz del modelo
- y: la respuesta
- qr: la descomposición qr
- singular.ok es un lógico que controla si se permiten o no los ajustes singulares,
- offset es un predictor conocido previamente que debe utilizarse en el modelo,
- . . . son argumentos adicionales que se pasan a las funciones de regresión de nivel inferior.
Ejemplo práctico de regresión lineal en R
Es suficiente teoría por ahora. Veamos cómo implementar todo esto. Vamos a ajustar un modelo lineal utilizando la regresión lineal en R con la ayuda de la función lm(). Después comprobaremos la calidad del ajuste del modelo. Vamos a utilizar el conjunto de datos de coches que se proporciona por defecto en el paquete base de R.
1. Comencemos con un análisis gráfico del conjunto de datos para familiarizarnos con él. Para ello dibujaremos un gráfico de dispersión y comprobaremos lo que nos dice sobre los datos.
Podemos utilizar la función scatter.smooth() para crear un gráfico de dispersión para el conjunto de datos.
scatter.smooth(x=cars$speed,y=cars$dist,main="TechVidvan Dist ~ Speed")
Salida
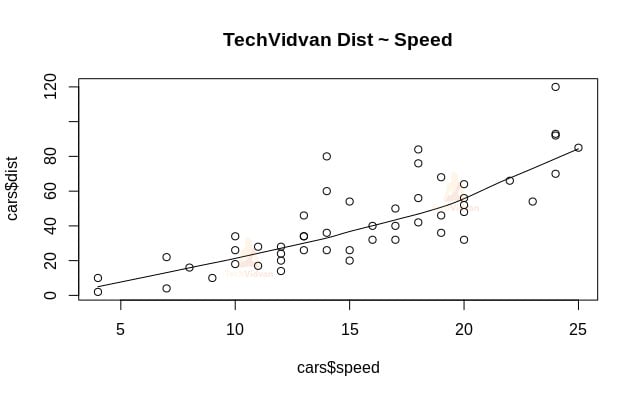
El gráfico de dispersión nos muestra una correlación positiva entre la distancia y la velocidad. Sugiere una relación lineal creciente entre las dos variables. Esto hace que los datos sean adecuados para la regresión lineal, ya que una relación lineal es un supuesto básico para ajustar un modelo lineal a los datos.
2. Ahora que hemos verificado que la regresión lineal es adecuada para los datos, podemos utilizar la función lm() para ajustar un modelo lineal a ellos.
Linear_model <- lm(dist~speed,data=cars)print(Linear_model)
Salida
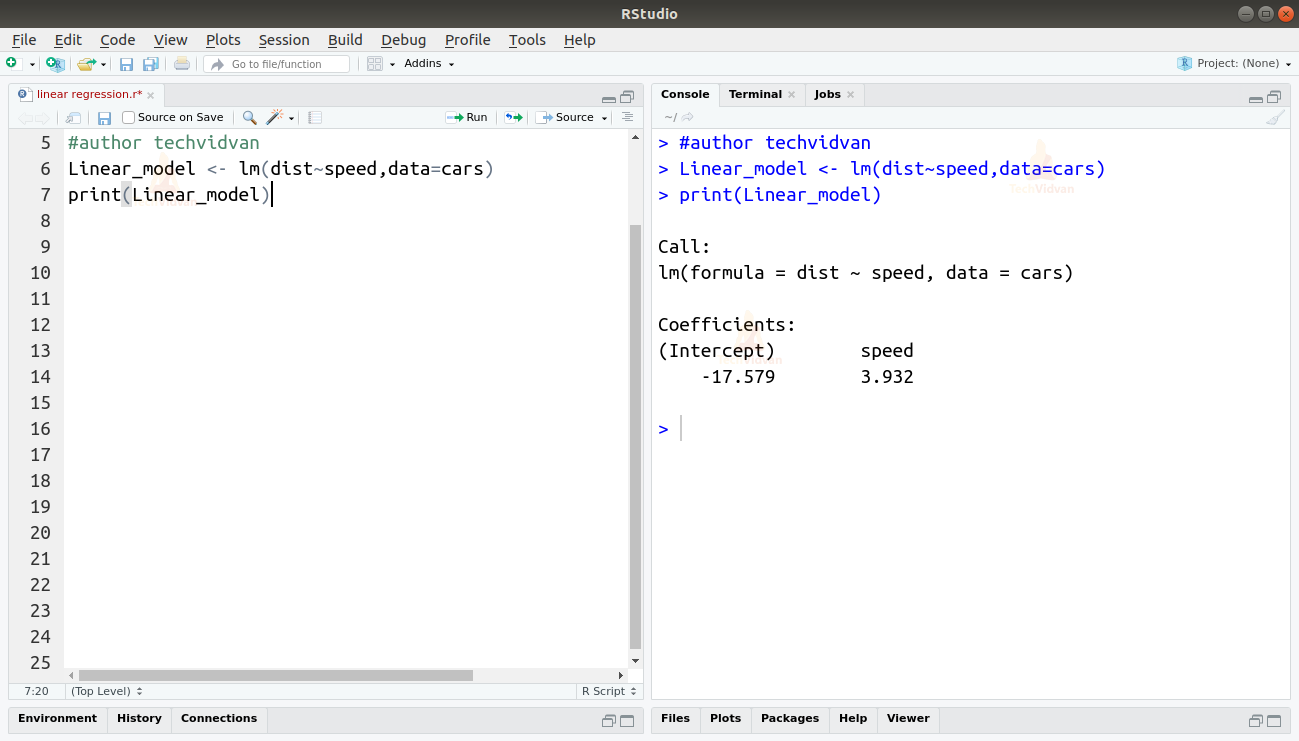
La salida de la función lm() nos muestra el intercepto y el coeficiente de velocidad. Definiendo así la relación lineal entre distancia y velocidad como:
Distancia=Intercepto+coeficiente*velocidad
Distancia=-17,579+3,932*velocidad
3. Ahora que hemos ajustado un modelo comprobemos la calidad o bondad del ajuste. Empecemos por comprobar el resumen del modelo lineal utilizando la función summary().
summary(Linear_model)
Salida
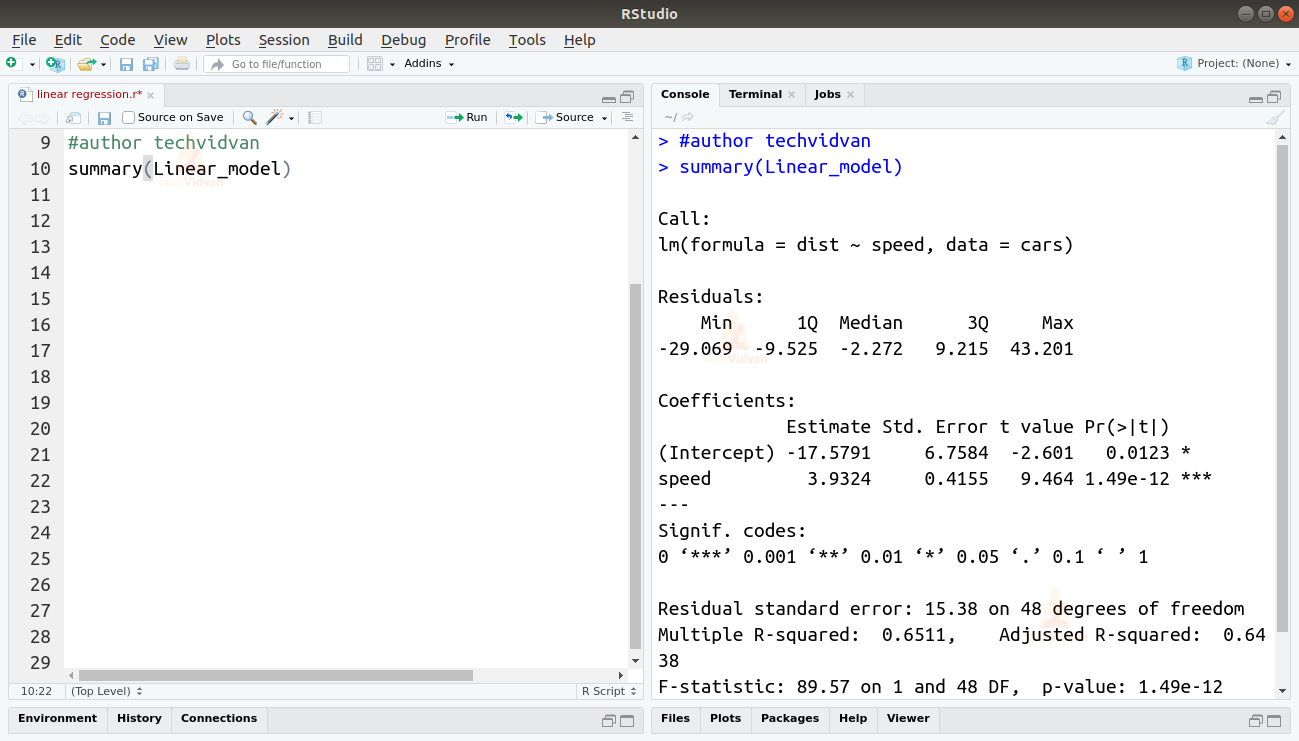
La función summary() nos da algunas medidas importantes para ayudar a diagnosticar el ajuste del modelo. El valor p es una medida importante de la bondad del ajuste de un modelo. Se dice que un modelo no está ajustado si el valor p es superior a un nivel de significación estadística predeterminado que, idealmente, es 0,05.
El resumen también nos proporciona el valor t. Cuanto mayor sea el valor t, mejor será el ajuste del modelo.
También podemos encontrar el AIC y el BIC utilizando las funciones AIC() y BIC().
AIC(Linear_model)BIC(Linear_model)
Salida
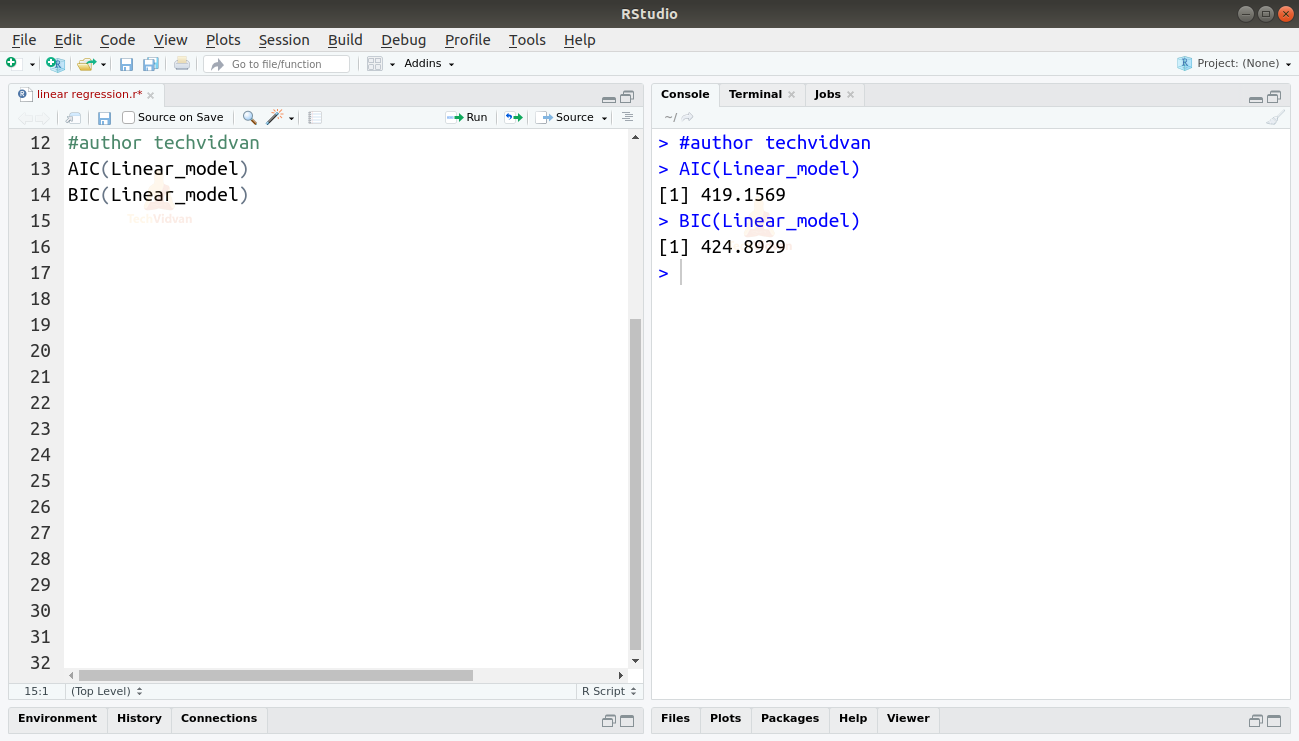
El modelo que da lugar a las puntuaciones AIC y BIC más bajas es el más preferido.
Resumen
En este capítulo de la serie de tutoriales de R de TechVidvan, aprendimos sobre la regresión lineal. Aprendimos sobre la regresión lineal simple y la regresión lineal múltiple. Luego estudiamos varias medidas para evaluar la calidad o precisión del modelo, como el R2, el R2 ajustado, el error estándar, la estadística F, el AIC y el BIC. Luego aprendimos a implementar la regresión lineal en R. Después comprobamos la calidad del ajuste del modelo en R.
Comparte tu valoración en Google si te ha gustado el tutorial de Regresión Lineal.