En los helados, los cristales de hielo pequeños y redondos son importantes para conseguir una textura suave y cremosa. En general, se sostiene que cuanto más rápida sea la velocidad de congelación, menor será el tamaño de los cristales de hielo. Sin embargo, para algunos materiales alimentarios existe un límite máximo para la velocidad de congelación. Si la congelación es demasiado rápida, se aplican tensiones mecánicas al material alimentario y puede producirse una fractura por congelación. En algunos casos, el proceso de congelación se utiliza para estructurar materiales, como el plato tradicional japonés kori-tofu, o andamios como los utilizados en la ingeniería de tejidos biológicos. Hace unos años, la WUR, junto con la TU Delft y Unilever, investigó el uso de la liofilización para estructurar sopas de verduras. Aquí, el tamaño de los cristales de hielo determina el tamaño del espacio de los poros después del secado, y ayuda a la rehidratación de las verduras cuando se mezclan con la sopa.
- Relación entre el tamaño de los cristales de hielo y la velocidad de congelación
- Modelo de campo de fases para el crecimiento de los cristales de hielo
- Tasa de congelación, composición y tamaño de los cristales de hielo
- Cuestiones de calidad de los alimentos para frutas y verduras congeladas
- Acerca del autor
Relación entre el tamaño de los cristales de hielo y la velocidad de congelación
Por lo tanto, desde la perspectiva de la calidad de los alimentos congelados, es importante conocer bien la relación entre el tamaño de los cristales de hielo y la velocidad de congelación. Sin embargo, sólo existen algunas relaciones empíricas entre la velocidad de congelación y el tamaño de los cristales de hielo. Además, en el caso de los alimentos manufacturados se utilizan otros medios para controlar el tamaño de los cristales de hielo, como los criopectantes, como los azúcares y las proteínas anticongelantes. Esto indica que cabe esperar una interacción entre la composición del material alimentario, la velocidad de congelación y el tamaño de los cristales de hielo, aunque en las relaciones empíricas la dependencia de la composición del alimento está ausente. Por lo tanto, Food & Biobased Research ha emprendido un proyecto de investigación dirigido a una comprensión más teórica de la relación entre la velocidad de congelación, la composición y el tamaño de los cristales de hielo utilizando simulaciones informáticas avanzadas.
Modelo de campo de fases para el crecimiento de los cristales de hielo
Para obtener este detalle de comprensión debemos sumergirnos en el rango micrométrico de la microestructura de los alimentos, donde los cristales de hielo individuales se resuelven en el modelo informático desarrollado, donde el crecimiento de los cristales se modela en función de la composición de la matriz. El método más avanzado en este campo es el modelo de campo de fases, que hemos utilizado para describir la estructuración de dispersiones como espumas y emulsiones, estabilizadas con emulsionantes. En el método de campo de fase se pueden modelar simultáneamente varios elementos individuales de las dispersiones, como gotas de emulsión, burbujas de espuma y cristales. El método permite fácilmente la ruptura y la coalescencia de estos elementos dispersos.
La fuerza del método reside en cómo trata la interfaz entre las fases dispersa y continua. Aquí, el método sigue la propuesta de un famoso físico holandés, vanderWaals, de incluir la interfaz en un marco termodinámico. Utilizando el método del campo de fases, hemos construido un modelo informático para la descripción de los cristales de hielo en una solución de sacarosa, cuyo comportamiento puede considerarse representativo del helado3. En investigaciones anteriores ya hemos aclarado la termodinámica de las soluciones acuosas de sacarosa4, así como la velocidad de transporte de agua en la solución de azúcar por difusión5. Así, para estas propiedades del material disponemos de teorías predictivas en función de la concentración de sacarosa para todo el rango de 0 a 100%.
Tasa de congelación, composición y tamaño de los cristales de hielo
Después de haber desarrollado el modelo informático, realizamos varias simulaciones por ordenador para investigar la relación entre la tasa de congelación, la composición y el tamaño de los cristales de hielo. Nos acercamos a una pequeña parte del material alimentario y sembramos varios núcleos para que crecieran cristales de hielo. A continuación, esta parte del material alimentario se sometió a una serie de velocidades de congelación. Se realizaron simulaciones para dos concentraciones diferentes de sacarosa -y una multitud de posiciones aleatorias diferentes de los núcleos- con el fin de obtener unas buenas estadísticas.
En la figura 1 se muestran instantáneas de estas simulaciones por ordenador. Los elementos dispersos de color azul oscuro son cristales de hielo individuales. La velocidad de congelación no es muy rápida, por lo que podemos suponer que los cristales de hielo se mantienen aproximadamente esféricos. Para entender los resultados de la simulación es importante saber que los cristales de hielo no contienen azúcar, por lo que el crecimiento de los cristales de hielo implica el aumento de las concentraciones de azúcar en la fase no congelada. El aumento de la concentración de azúcar conduce a un aumento del punto de congelación, dejando la matriz continua sin congelar.

Figura 1: Instantáneas del crecimiento de cristales de hielo en una solución de azúcar obtenidas mediante simulaciones por ordenador para diferentes velocidades de congelación (0,01, 0,03 y 0,10 K/s de arriba a abajo) observadas en diferentes momentos (de izquierda a derecha). Obsérvese la coalescencia de varios cristales de hielo, especialmente a la baja velocidad de congelación (arriba)
Al continuar la congelación, los cristales de hielo pueden chocar entre sí, lo que provoca un aumento de la concentración de azúcar en el líquido no congelado que se encuentra entre ellos, lo que lleva a la depresión del punto de congelación. Por lo tanto, se desarrolla una interfaz plana. Si la velocidad de congelación es demasiado lenta, los azúcares tienen tiempo de difundirse fuera de la zona de impacto y los cristales pueden unirse. En la fase inicial de la congelación, en la que el aumento local de la concentración de azúcar debido al crecimiento de los cristales de hielo es pequeño, se producen varios eventos de coalescencia. En la última fase de la congelación, la matriz no congelada se aproxima al estado vítreo, en el que la difusión del agua y el azúcar se detiene y el crecimiento de los cristales de hielo cesa.
A partir de las simulaciones hemos determinado el tamaño medio de los cristales de hielo y lo hemos representado gráficamente frente a la velocidad de congelación impuesta para dos concentraciones diferentes de sacarosa. Estos resultados se muestran en la Figura 2.
Se puede observar una considerable dispersión en los datos de la simulación, debido a la estocástica del proceso de nucleación. Sin embargo, realizando muchas ejecuciones de simulación, se puede ajustar una relación de ley de potencia fiable a través de los datos, que se muestran como las líneas que pasan por los puntos de datos en la Figura 2 (página 00). El ajuste muestra que los exponentes de la ley de potencia son 0,31 y 0,18 para una concentración inicial de azúcar del 10% y del 15%, respectivamente. Nuestra relación empírica anterior tiene un exponente de ley de potencia de 0,25, que se suponía independiente de la composición. El hecho de que el valor empírico se acerque bastante a los exponentes que hemos encontrado mediante simulación es muy alentador. Además, cabe destacar que el modelo de simulación no requirió ningún ajuste de parámetros, ya que se conocen todas las propiedades materiales y termodinámicas.
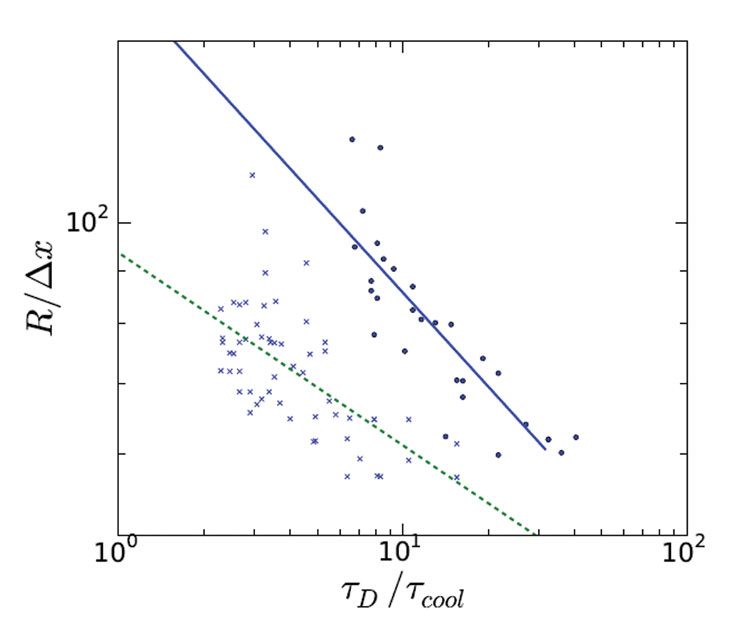
Figura 2: Tamaño medio de los cristales de hielo frente a la velocidad de congelación, para dos concentraciones iniciales de azúcar diferentes (10% y 15%, indicadas por línea sólida y discontinua). El radio se mide en unidades de la malla computacional, que es de unas 3 micras, y la velocidad de congelación 1/tcool se mide en términos de la velocidad de difusión del agua 1/tD. (a 0,01K/s si tD/tcool=1) Los puntos indican el tamaño medio de una sola simulación. Las líneas representan relaciones de ley de potencia, ajustadas a los datos de la simulación
Cuestiones de calidad de los alimentos para frutas y verduras congeladas
Alimentos & La investigación de base biológica concluye que el modelo tiene un gran grado de realismo. Además, existen teorías predictivas similares sobre las propiedades materiales y termodinámicas de muchos otros materiales alimentarios. Por consiguiente, el modelo es, en principio, aplicable a una multitud de otros materiales alimentarios. Sobre esta base, hemos puesto en marcha un nuevo proyecto de investigación que sigue desarrollando y adaptando el modelo a los materiales alimentarios congelados con estructura celular para investigar los problemas de calidad de los alimentos congelados de frutas y verduras. El modelo de campo de fase se integrará en un modelo multiescala -porque en los productos alimentarios surgirán diferencias locales en la velocidad de congelación- que debe resolverse con un enfoque avanzado, en el que el perfil de temperatura se calcule a escala del producto, y el crecimiento de los cristales de hielo a microescala. El modelo informático a macroescala llamará al modelo a microescala varias veces para una multitud de lugares. El modelo a microescala informará de la fracción de hielo local, mientras que el modelo a macroescala emitirá el gradiente de temperatura aplicado al modelo a microescala.
En este nuevo proyecto, Food & Biobased Research, no sólo nos centraremos en la etapa de congelación inicial, sino también en el almacenamiento congelado. Durante el almacenamiento pueden producirse fluctuaciones de temperatura debido al enfriamiento mecánico, o a la apertura y cierre de la puerta. Se supone que estas fluctuaciones de temperatura permiten que los cristales de hielo sigan creciendo, lo cual es desventajoso para la calidad del producto6. Nuestro objetivo es investigar si la reducción de la temperatura de almacenamiento hace que los alimentos sean menos sensibles a las fluctuaciones de temperatura, e incluso si se puede obtener una reducción del uso de energía. Además, incluso cuando la temperatura de almacenamiento es razonablemente constante, se produce un engrosamiento de la distribución de los cristales de hielo durante el almacenamiento en las condiciones convencionales de -18oC. Esto se demuestra en la comparación de los alimentos congelados mediante la congelación por chorro de aire y la congelación por desplazamiento de presión (PSF). Inicialmente, el tamaño de los cristales de hielo obtenidos mediante PSF es mucho menor que el obtenido mediante la congelación convencional por chorro de aire. Sin embargo, después de varias semanas de almacenamiento se encuentra poca diferencia en la distribución final del tamaño de los cristales de hielo, lo que indica que el engrosamiento se ha producido durante el almacenamiento de los alimentos PSF7.
En resumen, el nuevo modelo de simulación es una herramienta esencial para bucear en los posibles medios de la industria de los alimentos congelados para controlar la textura de los alimentos congelados y el tamaño de los cristales de hielo, en áreas como 1) la formulación del producto, 2) las condiciones de procesamiento y la tasa de congelación. Conociendo el impacto de la formulación y el procesamiento en la calidad de los alimentos congelados, se pueden evaluar nuevas estrategias para el almacenamiento de congelados debido a su impacto tanto en la calidad del producto como en el ahorro de energía.
- Voda, A., Homan, N., Witek, M., Duijster, A., van Dalen, G., van der Sman, R., Nijsse, J, van Vliet, L. Van As, H. & van Duynhoven, J. (2012). El impacto de la liofilización en la microestructura y las propiedades de rehidratación de la zanahoria. Food Research International, 49(2), 687-693
- van der Sman, R. G. M., Voda, A., van Dalen, G., & Duijster, A. (2013). Intercalación de cristales de hielo en alimentos congelados. Journal of Food Engineering, 116(2), 622-626
- van der Sman, R. G. M. (2016). Simulaciones de campo de fase del crecimiento de cristales de hielo en soluciones de azúcar. International Journal of Heat and Mass Transfer, 95, 153-161
- van der Sman, R. G. M., & Meinders, M. B. J. (2011). Predicción del diagrama de estado de mezclas de agua de almidón utilizando la teoría de volumen libre de Flory-Huggins. Soft Matter, 7(2), 429-442
- van der Sman, R. G. M., & Meinders, M. B. J. (2013). Difusividad de la humedad en materiales alimentarios. Food chemistry, 138(2), 1265-1274
- Regand, A & Goff HD. «Estructura y recristalización del hielo en sistemas modelo de helados estabilizados congelados». Food Hydrocolloids1 (2003): 95-102
- Fernández PP, Otero L, Martino MM ,Molina-García AD, & Sanz PD «Congelación por desplazamiento de alta presión: recristalización durante el almacenamiento» European Food Research and Technology 5 (2008): 1367-1377
Acerca del autor
Ruud van der Sman es licenciado en Física Aplicada por la Universidad Tecnológica de Delft y doctor en Ingeniería Agrícola por la Universidad de Wageningen. Trabaja como investigador senior en Food & Biobased Research, y profesor asistente a tiempo parcial en Food Process Engineering – ambos parte de Wageningen UR (Centro de Investigación de la Universidad &). Sus intereses de investigación comprenden la física de la materia blanda de los materiales alimentarios, la modelización informática de la estructuración de los alimentos a escala micrométrica y la modelización fisiológica. Sus conocimientos sobre la carne incluyen la termodinámica de la capacidad de retención de agua, la transferencia de calor y masa y la fisiología post mortem. www.wageningenur.nl/en/fbr