Un metamaterial electromagnético afecta a las ondas electromagnéticas que inciden o interactúan con sus características estructurales, que son más pequeñas que la longitud de onda. Para comportarse como un material homogéneo descrito con precisión por un índice de refracción efectivo, sus características deben ser mucho más pequeñas que la longitud de onda.
Para la radiación de microondas, las características son del orden de milímetros. Los metamateriales de frecuencias de microondas suelen construirse como conjuntos de elementos conductores de electricidad (como bucles de alambre) que tienen características inductivas y capacitivas adecuadas. Muchos metamateriales de microondas utilizan resonadores de anillo dividido.
Los metamateriales fotónicos están estructurados a escala nanométrica y manipulan la luz a frecuencias ópticas. Los cristales fotónicos y las superficies selectivas en frecuencia, como las rejillas de difracción, los espejos dieléctricos y los revestimientos ópticos, presentan similitudes con los metamateriales estructurados en sub-longitud de onda. Sin embargo, suelen considerarse distintos de los metamateriales, ya que su función surge de la difracción o la interferencia y, por tanto, no pueden aproximarse a un material homogéneo. Sin embargo, las estructuras materiales como los cristales fotónicos son eficaces en el espectro de luz visible. El centro del espectro visible tiene una longitud de onda de aproximadamente 560 nm (para la luz solar). Las estructuras de cristal fotónico suelen tener la mitad de este tamaño o menos, es decir, <280 nm.
Los metamateriales plasmónicos utilizan plasmones de superficie, que son paquetes de carga eléctrica que oscilan colectivamente en las superficies de los metales a frecuencias ópticas.
Las superficies selectivas de frecuencia (FSS) pueden presentar características de sub-longitud de onda y se conocen como conductores magnéticos artificiales (AMC) o superficies de alta impedancia (HIS). Las FSS presentan características inductivas y capacitivas que están directamente relacionadas con su estructura de sub-longitud de onda.
Los metamateriales electromagnéticos pueden dividirse en diferentes clases, como sigue:
Índice de refracción negativoEditar
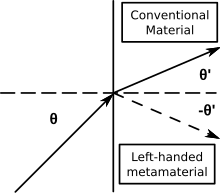
Los metamateriales de índice negativo (NIM) se caracterizan por tener un índice de refracción negativo. Otros términos para los NIM incluyen «medios de mano izquierda», «medios con un índice de refracción negativo» y «medios de onda descendente». Los NIM en los que el índice de refracción negativo surge de una permitividad y permeabilidad negativas simultáneamente también se conocen como metamateriales doblemente negativos o materiales doblemente negativos (DNG).
Suponiendo un material bien aproximado por una permitividad y permeabilidad reales, la relación entre la permitividad ϵ r {\displaystyle \epsilon _{r}}

, la permeabilidad μ r {{displaystyle \mu _{r}}

y el índice de refracción n viene dado por n = ± ϵ r μ r {\displaystyle \scriptstyle n=\pm {\sqrt {{epsilon _{mathrm {r}} }\mu _{mathrm {r} }}}}

. Todos los materiales transparentes no metamateriales conocidos (vidrio, agua, …) poseen ϵ r positivo {\displaystyle \epsilon _{r}}

y μ r {{displaystyle \mu _{r}}

. Por convención se utiliza la raíz cuadrada positiva para n. Sin embargo, algunos metamateriales de ingeniería tienen ϵ r {\displaystyle \epsilon _{r}}

y μ r < 0 {\displaystyle \mu _{r}<0}

. Porque el producto ϵ r μ r {\displaystyle \silon _{r}\mu _{r}}

es positivo, n es real. En tales circunstancias, es necesario tomar la raíz cuadrada negativa para n. Cuando tanto ϵ r {\displaystyle \epsilon _{r}}

y μ r {{displaystyle \mu _{r}}

son positivas (negativas), las ondas viajan en dirección hacia adelante (hacia atrás). Las ondas electromagnéticas no pueden propagarse en materiales con ϵ r {\displaystyle \epsilon _{r}}

y μ r {\displaystyle \mu _{r}}

de signo contrario a medida que el índice de refracción se vuelve imaginario. Este tipo de materiales son opacos para la radiación electromagnética y ejemplos de ello son los materiales plasmónicos como los metales (oro, plata, …).
Las consideraciones anteriores son simplistas para los materiales reales, que deben tener ϵ r de valor complejo.

y μ r {{publicación de estilo \Nmu _{r}}

. Las partes reales de ambos ϵ r {\displaystyle \epsilon _{r}}

y μ r {{publicación del estilo de \mu _{r}}

no tienen que ser negativos para que un material pasivo muestre una refracción negativa. De hecho, un índice de refracción negativo para ondas polarizadas circularmente también puede surgir de la quiralidad. Los metamateriales con n negativo tienen numerosas propiedades interesantes:
- La ley de Snell (n1sinθ1 = n2sinθ2) sigue describiendo la refracción, pero como n2 es negativo, los rayos incidentes y refractados están en el mismo lado de la normal de la superficie en una interfaz de materiales de índice positivo y negativo.
- La radiación de Cherenkov apunta en sentido contrario.
- El vector de Poynting promediado en el tiempo es antiparalelo a la velocidad de fase. Sin embargo, para que las ondas (energía) se propaguen, un -µ debe estar emparejado con un -ε para satisfacer la dependencia del número de onda de los parámetros del material k c = ω μ ϵ {\displaystyle kc=\omega {\sqrt {\mu \epsilon }}
.
El índice de refracción negativo se deriva matemáticamente del triplete vectorial E, H y k.
Para las ondas planas que se propagan en los metamateriales electromagnéticos, el campo eléctrico, el campo magnético y el vector de onda siguen una regla de la mano izquierda, la inversa del comportamiento de los materiales ópticos convencionales.
Hasta la fecha, sólo los metamateriales presentan un índice de refracción negativo.
Mono negativoEditar
Los metamateriales mono negativos (SNG) tienen una permitividad relativa negativa (εr) o una permeabilidad relativa negativa (µr), pero no ambas. Actúan como metamateriales cuando se combinan con un SNG diferente y complementario, actuando conjuntamente como un DNG.
Los medios épsilon negativos (ENG) muestran una εr negativa mientras que µr es positiva. Muchos plasmas exhiben esta característica. Por ejemplo, los metales nobles como el oro o la plata son ENG en los espectros infrarrojo y visible.
Los medios mu-negativos (MNG) muestran una εr positiva y una µr negativa. Los materiales girotrópicos o giromagnéticos presentan esta característica. Un material girotrópico es aquel que ha sido alterado por la presencia de un campo magnético cuasiestático, permitiendo un efecto magneto-óptico. El efecto magneto-óptico es un fenómeno en el que una onda electromagnética se propaga a través de dicho medio. En un material de este tipo, las polarizaciones elípticas que giran a la izquierda y a la derecha pueden propagarse a diferentes velocidades. Cuando la luz se transmite a través de una capa de material magneto-óptico, el resultado se denomina efecto Faraday: el plano de polarización puede girar, formando un rotador Faraday. El resultado de dicha reflexión se conoce como efecto Kerr magneto-óptico (no confundir con el efecto Kerr no lineal). Dos materiales girótropos con sentidos de rotación invertidos de las dos polarizaciones principales se denominan isómeros ópticos.
Al unir una losa de material ENG y otra de material MNG se obtienen propiedades como resonancias, tunelización anómala, transparencia y reflexión nula. Al igual que los materiales de índice negativo, los ENG son innatamente dispersivos, por lo que su εr, µr e índice de refracción n, son función de la frecuencia.
Metamateriales hiperbólicosEditar
Los metamateriales hiperbólicos (HMM) se comportan como un metal para cierta polarización o dirección de propagación de la luz y se comportan como un dieléctrico para la otra debido a los componentes del tensor de permitividad negativo y positivo, dando una anisotropía extrema. La relación de dispersión del material en el espacio del vector de onda forma un hiperboloide, por lo que se denomina metamaterial hiperbólico. La anisotropía extrema de los HMM conduce a la propagación direccional de la luz dentro y en la superficie. Los HMM han mostrado varias aplicaciones potenciales, como la detección, la obtención de imágenes, la dirección de señales ópticas y los efectos de resonancia de plasmón mejorados.
BandgapEdit
Los metamateriales de banda electromagnética (EBG o EBM) controlan la propagación de la luz. Esto se consigue con cristales fotónicos (PC) o con materiales zurdos (LHM). Los PC pueden prohibir totalmente la propagación de la luz. Ambas clases pueden permitir que la luz se propague en direcciones específicas y diseñadas, y ambas pueden diseñarse con brechas de banda en las frecuencias deseadas. El tamaño del periodo de los EBG es una fracción apreciable de la longitud de onda, lo que crea interferencias constructivas y destructivas.
Los PC se distinguen de las estructuras de sub-longitud de onda, como los metamateriales sintonizables, porque los PC derivan sus propiedades de sus características de bandgap. Los PC tienen un tamaño que coincide con la longitud de onda de la luz, frente a otros metamateriales que exponen una estructura de sub-longitud de onda. Además, los PC funcionan por difracción de la luz. En cambio, los metamateriales no utilizan la difracción.
Los PCs tienen inclusiones periódicas que inhiben la propagación de las ondas debido a la interferencia destructiva de las inclusiones por la dispersión. La propiedad de banda prohibida fotónica de los PCs los convierte en el análogo electromagnético de los cristales semiconductores electrónicos.
Los EBGs tienen el objetivo de crear estructuras dieléctricas periódicas de alta calidad y bajas pérdidas. Un EBG afecta a los fotones del mismo modo que los materiales semiconductores afectan a los electrones. Los PC son el material de banda prohibida perfecto, ya que no permiten la propagación de la luz. Cada unidad de la estructura periódica prescrita actúa como un átomo, aunque de un tamaño mucho mayor.
Las EBG están diseñadas para impedir la propagación de un ancho de banda de frecuencias asignado, para determinados ángulos de llegada y polarizaciones. Se han propuesto varias geometrías y estructuras para fabricar las propiedades especiales de los EBG. En la práctica es imposible construir un dispositivo EBG impecable.
Los EBG se han fabricado para frecuencias que van desde unos pocos gigahercios (GHz) hasta unos pocos terahercios (THz), regiones de frecuencias de radio, microondas e infrarrojo medio. Los desarrollos de aplicaciones EBG incluyen una línea de transmisión, pilas de madera hechas de barras dieléctricas cuadradas y varios tipos diferentes de antenas de baja ganancia.
Medio doblemente positivoEditar
Los medios doblemente positivos (DPS) se dan en la naturaleza, como los dieléctricos naturales. La permitividad y la permeabilidad magnética son ambas positivas y la propagación de las ondas se produce en la dirección de avance. Se han fabricado materiales artificiales que combinan propiedades DPS, ENG y MNG.
Bi-isotrópicos y bianisotrópicosEditar
La categorización de los metamateriales en doble o simple negativo, o doble positivo, asume normalmente que el metamaterial tiene respuestas eléctricas y magnéticas independientes descritas por ε y µ. Sin embargo, en muchos casos, el campo eléctrico causa polarización magnética, mientras que el campo magnético induce polarización eléctrica, conocida como acoplamiento magnetoeléctrico. Estos medios se denominan bi-isotrópicos. Los medios que exhiben acoplamiento magnetoeléctrico y que son anisotrópicos (que es el caso de muchas estructuras metamateriales), se denominan bi-anisotrópicos.
Cuatro parámetros del material son intrínsecos al acoplamiento magnetoeléctrico de los medios bi-isotrópicos. Son las intensidades de campo eléctrico (E) y magnético (H), y las densidades de flujo eléctrico (D) y magnético (B). Estos parámetros son ε, µ, κ y χ o permitividad, permeabilidad, fuerza de quiralidad y el parámetro de Tellegen, respectivamente. En este tipo de medios, los parámetros del material no varían con los cambios a lo largo de un sistema de coordenadas rotadas de las mediciones. En este sentido son invariantes o escalares.
Los parámetros magnetoeléctricos intrínsecos, κ y χ, afectan a la fase de la onda. El efecto del parámetro de quiralidad es dividir el índice de refracción. En los medios isótropos esto da lugar a la propagación de la onda sólo si ε y µ tienen el mismo signo. En medios bi-isotrópicos con χ asumido como cero, y κ un valor distinto de cero, aparecen resultados diferentes. Puede producirse una onda hacia atrás o una onda hacia delante. Alternativamente, pueden ocurrir dos ondas hacia adelante o dos ondas hacia atrás, dependiendo de la fuerza del parámetro de quiralidad.
En el caso general, las relaciones constitutivas para materiales bi-anisotrópicos dicen D = ϵ E + ξ H , {\displaystyle \mathbf {D} =\epsilon \mathbf {E} +\xi \mathbf {H} ,}

B = ζ E + μ H , {\displaystyle \mathbf {B} =\zeta \mathbf {E} +\mu \mathbf {E} +\mu \mathbf {H} ,}

donde ϵ {\displaystyle \epsilon }

y μ {\displaystyle \mu }

son los tensores de permitividad y permeabilidad, respectivamente, mientras que ξ {\displaystyle \xi }

y ζ {\displaystyle \zeta }

son los dos tensores magneto-eléctricos. Si el medio es recíproco, la permitividad y la permeabilidad son tensores simétricos, y ξ = – ζ T = – i κ T {\displaystyle \xi =-\zeta ^{T}=-i\kappa ^{T}}.

, donde κ {\displaystyle \kappa }

es el tensor quiral que describe la respuesta electromagnética quiral y magnetoeléctrica recíproca. El tensor quiral puede expresarse como κ = 1 3 tr ( κ ) I + N + J {\displaystyle \kappa ={tfrac {1}{3}}\operatorname {tr} (\kappa )I+N+J}

, donde tr ( κ ) {\displaystyle \operatorname {tr} (\kappa )}

es la traza de κ {\displaystyle \kappa }

, I es la matriz identidad, N es un tensor simétrico libre de trazas, y J es un tensor antisimétrico. Dicha descomposición nos permite clasificar la respuesta bianisotrópica recíproca y podemos identificar las siguientes tres clases principales: (i) medios quirales ( tr ( κ ) ≠ 0 , N ≠ 0 , J = 0 {\displaystyle \operatorname {tr} (\kappa )\N- 0,N\N- 0,J=0}

), (ii) medios pseudovirales ( tr ( κ ) = 0 , N ≠ 0 , J = 0 {\displaystyle \operatorname {tr} (\kappa )=0,N\neq 0,J=0}

), (iii) omega media ( tr ( κ ) = 0 , N = 0 , J ≠ 0 {\displaystyle \operatorname {tr} (\kappa )=0,N=0,J\neq 0}

).
ChiralEdit
La lateralidad de los metamateriales es una fuente potencial de confusión ya que la literatura sobre metamateriales incluye dos usos conflictivos de los términos zurdo y diestro. El primero se refiere a una de las dos ondas polarizadas circularmente que son los modos de propagación en los medios quirales. El segundo se refiere al triplete de campo eléctrico, campo magnético y vector de Poynting que surgen en los medios de índice de refracción negativo, que en la mayoría de los casos no son quirales.
En general, una respuesta electromagnética quiral y/o bianisotrópica es una consecuencia de la quiralidad geométrica 3D: los metamateriales tridimensionales-cirales están compuestos por la incrustación de estructuras tridimensionales-cirales en un medio anfitrión y muestran efectos de polarización relacionados con la quiralidad, como la actividad óptica y el dicroísmo circular. El concepto de quiralidad 2D también existe y se dice que un objeto plano es quiral si no puede superponerse a su imagen especular a menos que se levante del plano. Se ha observado que los metamateriales quiralizados en 2D que son anisotrópicos y con pérdidas presentan una transmisión (reflexión, absorción) asimétrica direccional de las ondas polarizadas circularmente debido a la dicrosimia de conversión circular. Por otro lado, la respuesta bianisotrópica puede surgir a partir de estructuras geométricas acirales que no poseen quiralidad intrínseca ni en 2D ni en 3D. Plum y sus colegas investigaron el acoplamiento magneto-eléctrico debido a la quiralidad extrínseca, donde la disposición de una estructura (aciral) junto con el vector de onda de radiación es diferente de su imagen especular, y observaron una actividad óptica lineal grande y sintonizable, una actividad óptica no lineal, una actividad óptica especular y un dicroísmo de conversión circular. Rizza et al. sugirieron metamateriales quirales 1D en los que el tensor quiral efectivo no es evanescente si el sistema es geométricamente quiral unidimensional (la imagen especular de toda la estructura no puede superponerse a ella utilizando traslaciones sin rotaciones).
Los metamateriales quirales 3D se construyen a partir de materiales o resonadores quirales en los que el parámetro de quiralidad efectivo κ {\displaystyle \kappa }

es distinto de cero. Las propiedades de propagación de las ondas en dichos metamateriales quirales demuestran que la refracción negativa puede realizarse en metamateriales con una fuerte quiralidad y ϵ r positivo {\displaystyle \epsilon _{r}}

y μ r {\displaystyle \mu _{r}}

. Esto se debe a que el índice de refracción n {\displaystyle n}

tiene valores distintos para las ondas polarizadas circularmente a la izquierda y a la derecha, dados por
n = ± ϵ r μ r ± κ {\displaystyle n=\pm {\sqrt {\epsilon _{r}\mu _{r}}\pm \kappa }

Se puede ver que se producirá un índice negativo para una polarización si κ {\displaystyle \kappa }

> ϵ r μ r {\displaystyle {\sqrt {\epsilon _{r}\mu _{r}}}}

. En este caso, no es necesario que uno o ambos ϵ r {\displaystyle \epsilon _{r}}

y μ r {\displaystyle \mu _{r}}

ser negativo para la propagación de la onda hacia atrás. Un índice de refracción negativo debido a la quiralidad fue observado por primera vez de forma simultánea e independiente por Plum et al. y Zhang et al. en 2009.
Basado en FSSEditar
Los metamateriales basados en superficies de frecuencia selectiva bloquean las señales en una banda de onda y pasan las de otra banda de onda. Se han convertido en una alternativa a los metamateriales de frecuencia fija. Permiten cambios opcionales de frecuencias en un solo medio, en lugar de las limitaciones restrictivas de una respuesta de frecuencia fija.
