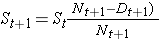A menudo estamos interesados en evaluar si existen diferencias en la supervivencia (o en la incidencia acumulada del evento) entre diferentes grupos de participantes. Por ejemplo, en un ensayo clínico con un resultado de supervivencia, podríamos estar interesados en comparar la supervivencia entre los participantes que reciben un nuevo fármaco en comparación con un placebo (o terapia estándar). En un estudio de observación, podría interesarnos comparar la supervivencia entre hombres y mujeres, o entre participantes con y sin un factor de riesgo concreto (por ejemplo, hipertensión o diabetes). Hay varias pruebas disponibles para comparar la supervivencia entre grupos independientes.
La prueba de rango logarítmico
La prueba de rango logarítmico es una prueba popular para comprobar la hipótesis nula de ausencia de diferencias en la supervivencia entre dos o más grupos independientes. La prueba compara toda la experiencia de supervivencia entre los grupos y puede considerarse como una prueba de si las curvas de supervivencia son idénticas (se superponen) o no. Las curvas de supervivencia se estiman para cada grupo, considerado por separado, mediante el método de Kaplan-Meier y se comparan estadísticamente mediante la prueba de rango logarítmico. Es importante señalar que existen diversas variantes del estadístico log rank test que son implementadas por diversos paquetes informáticos estadísticos (por ejemplo, SAS, R 4,6). Aquí presentamos una versión que está estrechamente relacionada con el estadístico de la prueba de chi-cuadrado y que compara los números observados con los esperados de eventos en cada punto de tiempo durante el período de seguimiento.
Ejemplo:
Se realiza un pequeño ensayo clínico para comparar dos tratamientos combinados en pacientes con cáncer gástrico avanzado. Veinte participantes con cáncer gástrico en estadio IV que consienten en participar en el ensayo son asignados aleatoriamente a recibir quimioterapia antes de la cirugía o quimioterapia después de la cirugía. El resultado primario es la muerte y los participantes son seguidos hasta 48 meses (4 años) después de la inscripción en el ensayo. Las experiencias de los participantes en cada brazo del ensayo se muestran a continuación.
|
Quimioterapia antes de la cirugía |
|
Quimioterapia después de la cirugía |
||
|---|---|---|---|---|
|
Mes de Muerte |
Mes de último contacto |
|
Mes de muerte |
Mes de último contacto |
|
8 |
8 |
|
33 |
48 |
|
12 |
32 |
|
28 |
48 |
|
26 |
20 |
|
41 |
25 |
|
14 |
40 |
|
|
37 |
|
21 |
|
|
|
48 |
|
27 |
|
|
|
25 |
|
|
|
|
|
43 |
Seis participantes del grupo de quimioterapia antes de la cirugía mueren en el transcurso del seguimiento.de seguimiento, en comparación con tres participantes del grupo de quimioterapia después de la cirugía. Otros participantes de cada grupo son seguidos durante un número variable de meses, algunos hasta el final del estudio a los 48 meses (en el grupo de quimioterapia después de la cirugía). Utilizando los procedimientos descritos anteriormente, primero construimos tablas de vida para cada grupo de tratamiento utilizando el enfoque de Kaplan-Meier.
Tabla de vida para el grupo que recibe quimioterapia antes de la cirugía
|
Tiempo, Meses |
Número de Riesgos Nt |
Número de Muertes Dt |
Número Censurado Ct |
Probabilidad de Supervivencia
|
|---|---|---|---|---|
|
0 |
10 |
|
|
1 |
|
8 |
10 |
1 |
1 |
0.900 |
|
12 |
8 |
1 |
|
0.788 |
|
14 |
7 |
1 |
|
0.675 |
|
20 |
6 |
|
1 |
0.675 |
|
21 |
5 |
1 |
|
0.540 |
|
26 |
4 |
1 |
|
0.405 |
|
27 |
3 |
1 |
|
0.270 |
|
32 |
2 |
|
1 |
0.270 |
|
40 |
1 |
|
1 |
0.270 |
Tabla de vida del grupo que recibe quimioterapia tras la cirugía
|
Tiempo, Meses |
Número de riesgo Nt |
Número de muertes Dt |
Número Censurado Ct |
Probabilidad de Supervivencia
|
|---|---|---|---|---|
|
0 |
10 |
|
|
1 |
|
25 |
10 |
|
2 |
1.000 |
|
28 |
8 |
1 |
|
0.875 |
|
33 |
7 |
1 |
|
0.750 |
|
37 |
6 |
|
1 |
0.750 |
|
41 |
5 |
1 |
|
0.600 |
|
43 |
4 |
|
1 |
0.600 |
|
48 |
3 |
|
3 |
0,600 |
A continuación se muestran las dos curvas de supervivencia.
Supervivencia en cada grupo de tratamiento
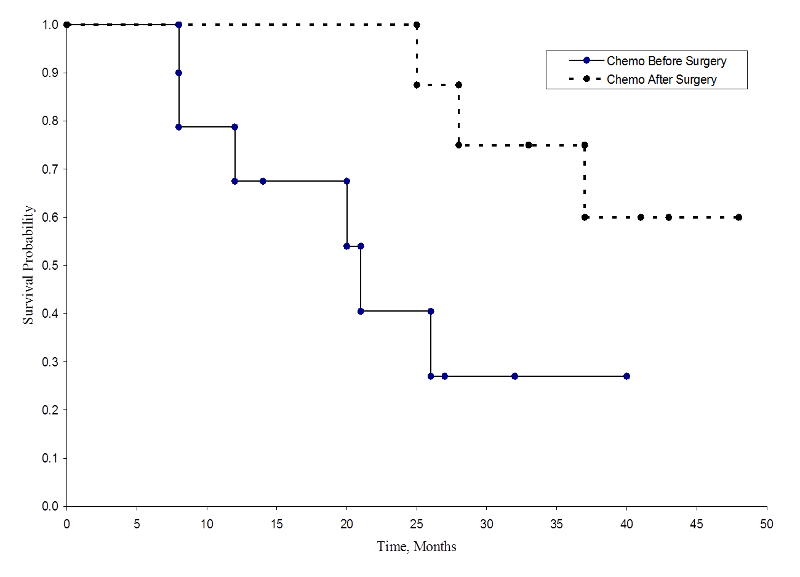
Las probabilidades de supervivencia para el grupo de quimioterapia después de la cirugía son mayores que las probabilidades de supervivencia para el grupo de quimioterapia antes de la cirugía, lo que sugiere un beneficio de supervivencia. Sin embargo, estas curvas de supervivencia se estiman a partir de muestras pequeñas. Para comparar la supervivencia entre grupos podemos utilizar la prueba de rango logarítmico. La hipótesis nula es que no hay diferencia en la supervivencia entre los dos grupos o que no hay diferencia entre las poblaciones en la probabilidad de muerte en cualquier punto. La prueba de rango logarítmico es una prueba no paramétrica y no hace suposiciones sobre las distribuciones de supervivencia. En esencia, la prueba de rango logarítmico compara el número observado de eventos en cada grupo con lo que se esperaría si la hipótesis nula fuera cierta (es decir, si las curvas de supervivencia fueran idénticas), si las curvas de supervivencia fueran idénticas).
H0: Las dos curvas de supervivencia son idénticas (o S1t = S2t) frente a H1: Las dos curvas de supervivencia no son idénticas (o S1t ≠ S2t, en cualquier momento t) (α=0,05).
La estadística log rank se distribuye aproximadamente como una estadística de prueba chi-cuadrado. Hay varias formas del estadístico de la prueba, y varían en términos de cómo se calculan. Utilizamos la siguiente:
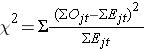
donde ΣOjt representa la suma del número observado de eventos en el jº grupo a lo largo del tiempo (por ejemplo, j=1,2) y ΣEjt representa la suma del número esperado de eventos en el jº grupo a lo largo del tiempo.
Las sumas de los números observados y esperados de eventos se calculan para cada tiempo de evento y se suman para cada grupo de comparación. El estadístico log rank tiene grados de libertad iguales a k-1, donde k representa el número de grupos de comparación. En este ejemplo, k=2 por lo que el estadístico de prueba tiene 1 grado de libertad.
Para calcular el estadístico de prueba necesitamos el número observado y esperado de eventos en cada momento del evento. El número observado de eventos proviene de la muestra y el número esperado de eventos se calcula asumiendo que la hipótesis nula es verdadera (es decir, que las curvas de supervivencia son idénticas).
Para generar los números esperados de eventos organizamos los datos en una tabla de vida con filas que representan cada tiempo de evento, independientemente del grupo en el que ocurrió el evento. También hacemos un seguimiento de la asignación de grupos. A continuación, estimamos la proporción de eventos que se producen en cada momento (Ot/Nt) utilizando los datos de ambos grupos combinados bajo el supuesto de que no hay diferencias en la supervivencia (es decir, asumiendo que la hipótesis nula es cierta). Multiplicamos estas estimaciones por el número de participantes en riesgo en ese momento en cada uno de los grupos de comparación (N1t y N2t para los grupos 1 y 2 respectivamente).
Específicamente, calculamos para cada tiempo de evento t, el número en riesgo en cada grupo, Njt (por ejemplo, donde j indica el grupo, j=1, 2) y el número de eventos (muertes), Ojt ,en cada grupo. La tabla siguiente contiene la información necesaria para realizar la prueba de rango logarítmico para comparar las curvas de supervivencia anteriores. El grupo 1 representa el grupo de quimioterapia antes de la cirugía, y el grupo 2 representa el grupo de quimioterapia después de la cirugía.
Datos para la prueba de rango logarítmico para comparar las curvas de supervivencia
|
Tiempo, Meses |
Número de eventos (muertes) en el grupo 1
N1t |
Número de eventos (muertes) en el grupo 2
N2t |
Número de eventos (muertes) en el grupo 1
O1t |
Número de eventos de eventos (muertes) en el grupo 2
O2t |
|---|---|---|---|---|
|
8 |
10 |
10 |
1 |
0 |
|
12 |
8 |
10 |
1 |
0 |
|
14 |
7 |
10 |
1 |
0 |
|
21 |
5 |
10 |
1 |
0 |
|
26 |
4 |
8 |
1 |
0 |
|
27 |
3 |
8 |
1 |
0 |
|
28 |
2 |
8 |
0 |
1 |
|
33 |
1 |
7 |
0 |
1 |
|
41 |
0 |
5 |
0 |
1 |
A continuación sumamos el número en riesgo, Nt = N1t+N2t, en cada momento del evento y el número de eventos observados (muertes), Ot = O1t+O2t, en cada momento del evento. A continuación, se calcula el número esperado de eventos en cada grupo. El número esperado de eventos se calcula en cada momento del evento como sigue:
E1t = N1t*(Ot/Nt) para el grupo 1 y E2t = N2t*(Ot/Nt) para el grupo 2. Los cálculos se muestran en la siguiente tabla.
Número esperado de eventos en cada grupo
|
Tiempo, Meses |
Número de riesgo en el grupo 1 N1t |
Número de riesgo en el grupo 2 N2t |
Número total de riesgo Nt |
Número de eventos en el grupo 1 O1t |
Número de eventos en el grupo 2 O2t |
Número total de eventos Ot |
Número esperado de eventos en Grupo 1 E1t = N1t*(Ot/Nt) |
Número esperado de eventos en Grupo 2 E2t = N2t*(Ot/Nt) |
|---|---|---|---|---|---|---|---|---|
|
8 |
10 |
10 |
20 |
1 |
0 |
1 |
0.500 |
0.500 |
|
12 |
8 |
10 |
18 |
1 |
0 |
1 |
0.444 |
0.556 |
|
14 |
7 |
10 |
17 |
1 |
0 |
1 |
0.412 |
0.588 |
|
21 |
5 |
10 |
15 |
1 |
0 |
1 |
0.333 |
0.667 |
|
26 |
4 |
8 |
12 |
1 |
0 |
1 |
0.333 |
0.667 |
|
27 |
3 |
8 |
11 |
1 |
0 |
1 |
0.273 |
0.727 |
|
28 |
2 |
8 |
10 |
0 |
1 |
1 |
0.200 |
0.800 |
|
33 |
1 |
7 |
8 |
0 |
1 |
1 |
0.125 |
0.875 |
|
41 |
0 |
5 |
5 |
0 |
1 |
1 |
0.000 |
1.000 |
A continuación sumamos los números observados de eventos en cada grupo (∑O1t y ΣO2t) y los números esperados de eventos en cada grupo (ΣE1t y ΣE2t) a lo largo del tiempo. Estos datos se muestran en la fila inferior de la siguiente tabla.
Número total observado y esperado de observados en cada grupo
|
Tiempo, Meses |
Número en riesgo en el Grupo 1 N1t |
Número en riesgo en el Grupo 2 N2t |
Número total en riesgo Nt |
Número de eventos en el grupo 1 O1t |
Número de eventos en el grupo 2 O2t |
Número total de eventos Ot |
Número esperado de eventos en Grupo 1 E1t = N1t*(Ot/Nt) |
Número esperado de eventos en Grupo 2 E2t = N2t*(Ot/Nt) |
|---|---|---|---|---|---|---|---|---|
|
8 |
10 |
10 |
20 |
1 |
0 |
1 |
0.500 |
0.500 |
|
12 |
8 |
10 |
18 |
1 |
0 |
1 |
0.444 |
0.556 |
|
14 |
7 |
10 |
17 |
1 |
0 |
1 |
0.412 |
0.588 |
|
21 |
5 |
10 |
15 |
1 |
0 |
1 |
0.333 |
0.667 |
|
26 |
4 |
8 |
12 |
1 |
0 |
1 |
0.333 |
0.667 |
|
27 |
3 |
8 |
11 |
1 |
0 |
1 |
0.273 |
0.727 |
|
28 |
2 |
8 |
10 |
0 |
1 |
1 |
0.200 |
0.800 |
|
33 |
1 |
7 |
8 |
0 |
1 |
1 |
0.125 |
0.875 |
|
41 |
0 |
5 |
5 |
0 |
1 |
1 |
0.000 |
1.000 |
|
|
6 |
3 |
|
2.620 |
6,380 |
Ahora podemos calcular la estadística de la prueba:
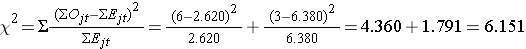
La estadística de la prueba se distribuye aproximadamente como chi-cuadrado con 1 grado de libertad. Así, el valor crítico de la prueba puede encontrarse en la tabla de Valores Críticos de la Distribución Χ2.
Para esta prueba la regla de decisión es Rechazar H0 si Χ2 > 3,84. Observamos que Χ2 = 6,151, que supera el valor crítico de 3,84. Por lo tanto, rechazamos H0. Tenemos evidencia significativa, α=0,05, para mostrar que las dos curvas de supervivencia son diferentes.
Ejemplo:
Un investigador desea evaluar la eficacia de una intervención breve para prevenir el consumo de alcohol en el embarazo. Las mujeres embarazadas con un historial de consumo excesivo de alcohol son reclutadas en el estudio y aleatorizadas para recibir la intervención breve centrada en la abstinencia de alcohol o la atención prenatal estándar. El resultado de interés es la recaída en el consumo de alcohol. Las mujeres son reclutadas en el estudio aproximadamente a las 18 semanas de gestación y son seguidas a lo largo del embarazo hasta el parto (aproximadamente 39 semanas de gestación). Los datos se muestran a continuación e indican si las mujeres recaen en el consumo de alcohol y, en caso afirmativo, el momento de su primer consumo medido en el número de semanas desde la aleatorización. En el caso de las mujeres que no recaen, se registra el número de semanas desde la aleatorización en que no beben.
|
Cuidado prenatal estándar |
|
Intervención breve |
||
|---|---|---|---|---|
|
Recaída |
Sin recaída |
|
Recaída |
Sin recaída |
|
19 |
20 |
|
16 |
21 |
|
6 |
19 |
|
21 |
15 |
|
5 |
17 |
|
7 |
18 |
|
4 |
14 |
|
|
18 |
|
|
|
|
|
5 |
La cuestión de interés es si existe una diferencia en el tiempo hasta la recaída entre las mujeres asignadas a la atención prenatal estándar en comparación con las asignadas a la intervención breve.
- Paso 1.
Establezca las hipótesis y determine el nivel de significación.
H0: El tiempo libre de recaída es idéntico entre los grupos frente a
H1: El tiempo libre de recaída no es idéntico entre los grupos (α=0,05)
- Paso 2.
Seleccione la estadística de prueba apropiada.
El estadístico de prueba para la prueba de rango logarítmico es
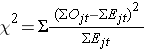
- Paso 3.
Establezca la regla de decisión.
El estadístico de prueba sigue una distribución chi-cuadrado, por lo que encontramos el valor crítico en la tabla de valores críticos para la distribución Χ2) para df=k-1=2-1=1 y α=0,05. El valor crítico es 3,84 y la regla de decisión es rechazar H0 si Χ2 > 3,84.
- Paso 4.
Calcular el estadístico de la prueba.
Para calcular el estadístico de la prueba, organizamos los datos según los tiempos del evento (recaída) y determinamos el número de mujeres en riesgo en cada grupo de tratamiento y el número que recae en cada tiempo de recaída observado. En la siguiente tabla, el grupo 1 representa a las mujeres que reciben atención prenatal estándar y el grupo 2 representa a las mujeres que reciben la intervención breve.
|
Tiempo, Semanas |
Número de recaídas – Grupo 1 N1t |
Número de recaídas – Grupo 2 N2t |
Número de recaídas – Grupo 1 O1t |
Número de recaídas – Grupo 2 O2t |
|---|---|---|---|---|
|
4 |
8 |
8 |
1 |
0 |
|
5 |
7 |
8 |
1 |
0 |
|
6 |
6 |
7 |
1 |
0 |
|
7 |
5 |
7 |
0 |
1 |
|
16 |
4 |
5 |
0 |
1 |
|
19 |
3 |
2 |
1 |
0 |
|
21 |
0 |
2 |
0 |
1 |
A continuación sumamos el número en riesgo, 
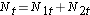, en cada momento del evento, el número de eventos observados (recaídas), 
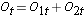, en cada momento del evento y determinamos el número esperado de recaídas en cada grupo en cada momento del evento utilizando 
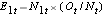y 
.
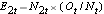A continuación, sumamos los números observados de eventos en cada grupo (ΣO1t y ΣO2t) y los números esperados de eventos en cada grupo (ΣE1t y ΣE2t) a lo largo del tiempo. Los cálculos para los datos de este ejemplo se muestran a continuación.
| Tiempo, Semanas |
Número de Grupo de Riesgo 1 N1t |
Número de Grupo de Riesgo 2 N2t |
Número Total de Riesgo Nt |
Número de recaídas Grupo 1 O1t |
Número de recaídas Grupo 2 O2t |
Número total de recaídas Ot |
Número esperado de recaídas en el grupo 1
|
Número esperado de recaídas en el grupo 2
|
|---|---|---|---|---|---|---|---|---|
|
4 |
8 |
8 |
16 |
1 |
0 |
1 |
0.500 |
0.500 |
|
5 |
7 |
8 |
15 |
1 |
0 |
1 |
0.467 |
0.533 |
|
6 |
6 |
7 |
13 |
1 |
0 |
1 |
0.462 |
0.538 |
|
7 |
5 |
7 |
12 |
0 |
1 |
1 |
0.417 |
0.583 |
|
16 |
4 |
5 |
9 |
0 |
1 |
1 |
0.444 |
0.556 |
|
19 |
3 |
2 |
5 |
1 |
0 |
1 |
0.600 |
0.400 |
|
21 |
0 |
2 |
2 |
0 |
1 |
1 |
0.000 |
1.000 |
|
|
|
|
|
4 |
3 |
|
2.890 |
4.110 |
Calculamos ahora el estadístico de la prueba:
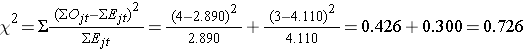
- Paso 5.
Conclusión. No rechazar H0 porque 0,726 < 3,84. No tenemos evidencia estadísticamente significativa a α=0,05, para mostrar que el tiempo hasta la recaída es diferente entre los grupos.
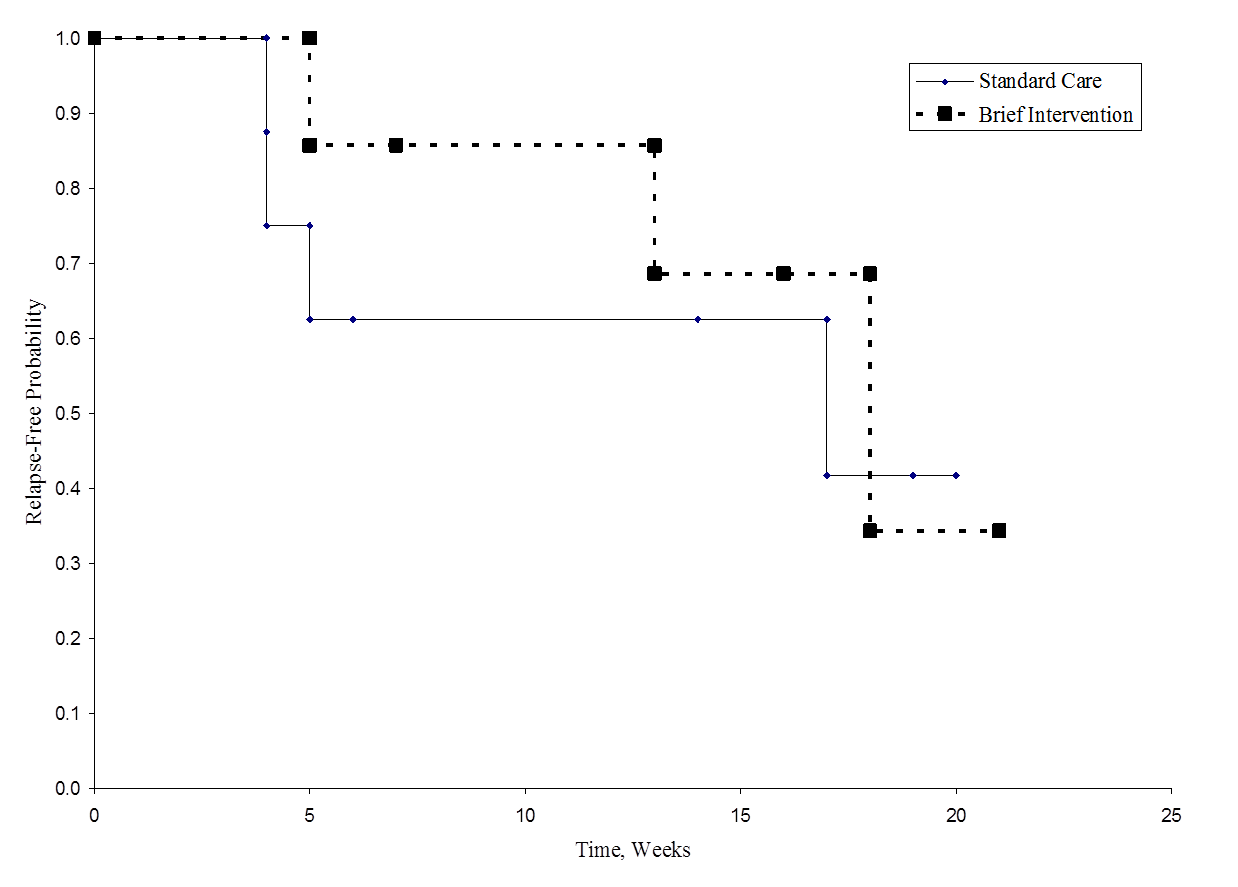
La figura siguiente muestra la supervivencia (tiempo libre de recaída) en cada grupo. Obsérvese que las curvas de supervivencia no muestran mucha separación, lo que es coherente con los resultados no significativos de la prueba de hipótesis.
Tiempo libre de recaída en cada grupo
Como se ha señalado, existen diversas variaciones del estadístico log rank. Algunos paquetes de cálculo estadístico utilizan el siguiente estadístico de prueba para la prueba de rango logarítmico para comparar dos grupos independientes:
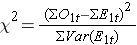
donde ΣO1t es la suma del número observado de eventos en el grupo 1, y ΣE1t es la suma del número esperado de eventos en el grupo 1 tomado sobre todos los tiempos de eventos. El denominador es la suma de las varianzas de los números esperados de eventos en cada momento del evento, que se calcula de la siguiente manera:
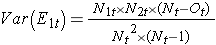
Hay otras versiones del estadístico log rank, así como otras pruebas para comparar las funciones de supervivencia entre grupos independientes.7-9 Por ejemplo, una prueba muy popular es la prueba de Wilcoxon modificada, que es sensible a las diferencias más grandes en los riesgos en las primeras etapas del seguimiento en comparación con las últimas.10
volver al principio | página anterior | página siguiente