#InsideRL
En un problema típico de Aprendizaje por Refuerzo (RL), hay un aprendiz y un tomador de decisiones llamado agente y el entorno con el que interactúa se llama ambiente. El entorno, a cambio, proporciona recompensas y un nuevo estado basado en las acciones del agente. Por lo tanto, en el aprendizaje por refuerzo, no enseñamos a un agente cómo debe hacer algo, sino que le presentamos recompensas, ya sean positivas o negativas, en función de sus acciones. Así pues, nuestra pregunta fundamental para este blog es cómo formulamos matemáticamente cualquier problema en RL. Aquí es donde entra el Proceso de Decisión de Markov (MDP).

Antes de responder a nuestra pregunta raíz es decir. Cómo formulamos matemáticamente los problemas de RL (usando MDP), necesitamos desarrollar nuestra intuición sobre :
- La relación Agente-Entorno
- Propiedad de Markov
- Proceso de Markov y cadenas de Markov
- Proceso de Recompensa de Markov (MRP)
- Ecuación de Bellman
- Proceso de Recompensa de Markov
¡Toma tu café y no pares hasta que estés orgulloso!🧐
La Relación Agente-Ambiente
Primero veamos algunas definiciones formales :
Agente : Programas de software que toman decisiones inteligentes y son los aprendices en RL. Estos agentes interactúan con el entorno mediante acciones y reciben recompensas en función de sus acciones.
Entorno :Es la demostración del problema a resolver.Ahora bien, podemos tener un entorno del mundo real o un entorno simulado con el que nuestro agente interactuará.

Estado : Es la posición de los agentes en un paso de tiempo específico en el entorno.Así, cada vez que un agente realiza una acción el entorno le da al agente una recompensa y un nuevo estado al que llegó el agente al realizar la acción.
Cualquier cosa que el agente no pueda cambiar arbitrariamente se considera parte del entorno. En términos sencillos, las acciones pueden ser cualquier decisión que queramos que el agente aprenda y el estado puede ser cualquier cosa que pueda ser útil para elegir acciones. No asumimos que todo lo que hay en el entorno es desconocido para el agente, por ejemplo, el cálculo de la recompensa se considera parte del entorno aunque el agente sepa un poco cómo se calcula su recompensa en función de sus acciones y de los estados en los que se toman. Esto se debe a que las recompensas no pueden ser modificadas arbitrariamente por el agente. A veces, el agente puede ser plenamente consciente de su entorno pero aún así le resulta difícil maximizar la recompensa, como si supiéramos jugar al cubo de Rubik pero no pudiéramos resolverlo. Por lo tanto, podemos decir con seguridad que la relación agente-entorno representa el límite del control del agente y no su conocimiento.
La propiedad de Markov
Transición : Pasar de un estado a otro se llama Transición.
Probabilidad de Transición: La probabilidad de que el agente pase de un estado a otro se llama probabilidad de transición.
La propiedad de Markov establece que :
«El futuro es independiente del pasado dado el presente»
Matemáticamente podemos expresar esta afirmación como :
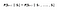
S denota el estado actual del agente y s denota el siguiente estado. Lo que esta ecuación significa es que la transición del estado S a S es totalmente independiente del pasado. Por lo tanto, el RHS de la ecuación significa lo mismo que el LHS si el sistema tiene una propiedad de Markov. Intuitivamente significa que nuestro estado actual ya captura la información de los estados pasados.
Probabilidad de Transición de Estado :
Como ahora conocemos la probabilidad de transición podemos definir la Probabilidad de Transición de Estado como sigue :
Para el Estado Markov de S a S es decir cualquier otro estado sucesor , la probabilidad de transición de estado viene dada por

Podemos formular la probabilidad de Transición de Estado en una matriz de probabilidad de Transición de Estado por :

Cada fila de la matriz representa la probabilidad de pasar de nuestro estado original o inicial a cualquier estado sucesor.La suma de cada fila es igual a 1.
Proceso de Markov o cadenas de Markov
El proceso de Markov es un proceso aleatorio sin memoria, es decir, una secuencia de un estado aleatorio S,S,….S con una propiedad de Markov.La dinámica del entorno puede definirse completamente utilizando los estados(S) y la matriz de probabilidad de transición(P).
¿Pero qué significa proceso aleatorio?
Para responder a esta pregunta veamos un ejemplo:
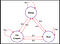
Las aristas del árbol denotan la probabilidad de transición. De esta cadena tomemos alguna muestra. Ahora, supongamos que estamos durmiendo y que según la distribución de probabilidad hay un 0,6 de probabilidad de que corramos y un 0,2 de que durmamos más y de nuevo un 0,2 de que comamos un helado. Del mismo modo, podemos pensar en otras secuencias que podemos muestrear de esta cadena.
Algunas muestras de la cadena :
- Dormir – Correr – Helado – Dormir
- Dormir – Helado – Helado – Correr
En las dos secuencias anteriores lo que vemos es que obtenemos un conjunto aleatorio de Estados(S) (es decir, Dormir,Helado,Dormir ) cada vez que ejecutamos la cadena.Espero que ahora esté claro por qué el proceso de Markov se llama conjunto aleatorio de secuencias.
Antes de pasar al proceso de recompensa de Markov vamos a ver algunos conceptos importantes que nos ayudarán a entender los MRP.
Recompensas y retornos
Las recompensas son los valores numéricos que el agente recibe al realizar alguna acción en algún estado(s) del entorno. El valor numérico puede ser positivo o negativo basado en las acciones del agente.
En el aprendizaje por refuerzo, nos preocupamos por maximizar la recompensa acumulativa (todas las recompensas que el agente recibe del entorno) en lugar de, la recompensa que el agente recibe del estado actual (también llamada recompensa inmediata). Esta suma total de la recompensa que el agente recibe del entorno se llama rendimiento.
Podemos definir los retornos como :
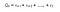
r es la recompensa recibida por el agente en el paso de tiempo t mientras realiza una acción(a) para pasar de un estado a otro. Del mismo modo, r es la recompensa recibida por el agente en el paso de tiempo t al realizar una acción para pasar a otro estado. Y, r es la recompensa recibida por el agente en el último paso de tiempo al realizar una acción para pasar a otro estado.
Tareas Espisódicas y Continuas
Tareas Espisódicas: Son las tareas que tienen un estado terminal (estado final).Podemos decir que tienen estados finitos. Por ejemplo, en los juegos de carreras, empezamos el juego (empieza la carrera) y lo jugamos hasta que el juego termina (¡la carrera termina!). Esto se llama un episodio. Una vez que reiniciamos el juego, éste partirá de un estado inicial y, por tanto, cada episodio es independiente.
Tareas continuas : Estas son las tareas que no tienen fin, es decir, no tienen ningún estado terminal.Este tipo de tareas nunca terminarán.Por ejemplo, ¡Aprender a codificar!
Ahora, es fácil calcular los rendimientos de las tareas episódicas ya que eventualmente terminarán pero qué pasa con las tareas continuas, ya que seguirán y seguirán para siempre. ¡Los rendimientos de la suma hasta el infinito! Entonces, ¿cómo definimos los rendimientos de las tareas continuas?
Aquí es donde necesitamos el factor de descuento(ɤ).
Factor de descuento (ɤ): Determina la importancia que hay que dar a la recompensa inmediata y a las recompensas futuras. Básicamente nos ayuda a evitar el infinito como recompensa en tareas continuas. Tiene un valor entre 0 y 1. Un valor de 0 significa que se da más importancia a la recompensa inmediata y un valor de 1 significa que se da más importancia a las recompensas futuras. En la práctica, un factor de descuento de 0 nunca aprenderá, ya que sólo tiene en cuenta la recompensa inmediata, y un factor de descuento de 1 seguirá con las recompensas futuras, lo que puede llevar al infinito. Por lo tanto, el valor óptimo del factor de descuento está entre 0,2 y 0,8.
Entonces, podemos definir los rendimientos utilizando el factor de descuento de la siguiente manera :(Digamos que esta es la ecuación 1 ,ya que vamos a utilizar esta ecuación en más adelante para derivar la ecuación de Bellman)

Entendámoslo con un ejemplo,¡Supongamos que usted vive en un lugar donde se enfrenta a la escasez de agua por lo que si alguien viene a usted y dice que él le dará 100 litros de agua!(¡suponga por favor!) para las próximas 15 horas en función de algún parámetro (ɤ).Veamos dos posibilidades : (Digamos que esta es la ecuación 1 ,ya que vamos a utilizar esta ecuación en más adelante para derivar la Ecuación de Bellman)
Una con factor de descuento (ɤ) 0.8 :
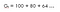
Esto significa que debemos esperar hasta la hora 15 porque la disminución no es muy significativa, por lo que todavía vale la pena ir hasta el final.Por lo tanto, si el factor de descuento es cercano a 1 entonces haremos un esfuerzo para ir hasta el final ya que la recompensa es de importancia significativa.
Segundo, con factor de descuento (ɤ) 0.2 :
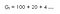
Esto significa que estamos más interesados en las recompensas tempranas ya que las recompensas son significativamente bajas a la hora.Por lo tanto, es posible que no queramos esperar hasta el final (hasta la hora 15) ya que no tendrá ningún valor.Por lo tanto, si el factor de descuento es cercano a cero entonces las recompensas inmediatas son más importantes que las futuras.
Entonces, ¿qué valor del factor de descuento utilizar?
Depende de la tarea para la que queremos entrenar a un agente. Supongamos que, en una partida de ajedrez, el objetivo es derrotar al rey del adversario. Si damos importancia a las recompensas inmediatas, como una recompensa por la derrota del peón de cualquier jugador del oponente, entonces el agente aprenderá a realizar estas submetas sin importar si sus jugadores también son derrotados. Por lo tanto, en esta tarea las recompensas futuras son más importantes. Hasta ahora hemos visto cómo la cadena de Markov define la dinámica de un entorno utilizando un conjunto de estados (S) y una matriz de probabilidad de transición (P), pero sabemos que el aprendizaje por refuerzo tiene como objetivo maximizar la recompensa.
Proceso de recompensa de Markov : Como su nombre indica, los MDP son las cadenas de Markov con juicio de valores.Básicamente, obtenemos un valor de cada estado en el que se encuentra nuestro agente.
Matemáticamente, definimos el Proceso de Recompensa de Markov como :
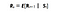
Lo que significa esta ecuación es cuánta recompensa (Rs) obtenemos de un estado particular S. Esto nos dice la recompensa inmediata de ese estado particular en el que está nuestro agente. Como veremos en la siguiente historia cómo maximizamos estas recompensas de cada estado en el que se encuentra nuestro agente. En términos simples, maximizar la recompensa acumulada que obtenemos de cada estado.
Definimos MRP como (S,P,R,ɤ) ,donde :
- S es un conjunto de estados,
- P es la Matriz de Probabilidad de Transición,
- R es la función de Recompensa , que vimos anteriormente,
- ɤ es el factor de descuento
Proceso de Decisión de Markov
Ahora, vamos a desarrollar nuestra intuición para la Ecuación de Bellman y el Proceso de Decisión de Markov.
Función política y función de valor
La función de valor determina lo bueno que es para el agente estar en un estado particular. Por supuesto, para determinar qué tan bueno será estar en un estado particular debe depender de algunas acciones que tomará. Aquí es donde entra la política. Una política define qué acciones realizar en un estado particular s.

Una política es una función simple, que define una distribución de probabilidad sobre Acciones (a∈ A) para cada estado (s ∈ S). Si un agente en el tiempo t sigue una política π entonces π(a|s) es la probabilidad de que el agente con tomar una acción (a ) en un paso de tiempo particular (t).En el Aprendizaje por Refuerzo la experiencia del agente determina el cambio de política. Matemáticamente, una política se define como sigue :
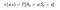
Ahora, cómo encontramos un valor de un estado.El valor del estado s, cuando el agente está siguiendo una política π que se denota por vπ(s) es el rendimiento esperado a partir de s y siguiendo una política π para los próximos estados, hasta que llegamos al estado terminal.Podemos formular esto como :(Esta función también se llama Función Estado-Valor)

Esta ecuación nos da los retornos esperados empezando por el estado(s) y yendo a los estados sucesivos después, con la política π. Una cosa a tener en cuenta es que los rendimientos que obtenemos son estocásticos mientras que el valor de un estado no es estocástico. Es la expectativa de los retornos desde el estado inicial s y después, a cualquier otro estado. Y también hay que tener en cuenta que el valor del estado terminal (si lo hay) es cero. Veamos un ejemplo :
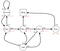
Supongamos que nuestro estado de inicio es la Clase 2, y pasamos a la Clase 3 y luego al Pase y al Sueño.En resumen, Clase 2 > Clase 3 > Pase > Sueño.
Nuestra rentabilidad esperada es con factor de descuento 0,5:
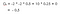
Nota:Es -2 + (-2 * 0.5) + 10 * 0,25 + 0 en lugar de -2 * -2 * 0,5 + 10 * 0,25 + 0.Entonces el valor de la clase 2 es -0,5 .
Ecuación de Bellman para la función de valor
La ecuación de Bellman nos ayuda a encontrar las políticas óptimas y la función de valor.Sabemos que nuestra política cambia con la experiencia por lo que tendremos diferentes funciones de valor según las diferentes políticas.La función de valor óptima es aquella que da el máximo valor en comparación con todas las demás funciones de valor.
La Ecuación de Bellman establece que la función de valor puede descomponerse en dos partes:
- Recompensa inmediata, R
- Valor descontado de los estados sucesores,
Matemáticamente, podemos definir la Ecuación de Bellman como :

Entendamos lo que dice esta ecuación con ayuda de un ejemplo :
Supongamos, que hay un robot en algún estado (s) y luego se mueve de este estado a algún otro estado (s’). Ahora, la pregunta es qué tan bueno fue para el robot estar en el estado (s). Usando la ecuación de Bellman, podemos que es la expectativa de recompensa que obtuvo al dejar el estado (s) más el valor del estado (s’) al que se movió.
Veamos otro ejemplo :
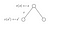
Queremos conocer el valor del estado s.El valor del estado s es la recompensa que obtuvimos al salir de ese estado, más el valor descontado del estado en el que aterrizamos multiplicado por la probabilidad de transición de que pasemos a él.
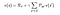
La ecuación anterior puede expresarse en forma matricial como sigue :

Donde v es el valor del estado en el que estábamos, que es igual a la recompensa inmediata más el valor descontado del siguiente estado multiplicado por la probabilidad de pasar a ese estado.
La complejidad del tiempo de ejecución de este cálculo es O(n³). Por lo tanto, está claro que no es una solución práctica para resolver MRPs más grandes (lo mismo para MDPs, también).En Blogs posteriores, veremos métodos más eficientes como la Programación Dinámica (iteración del valor e iteración de la política), los métodos de Monte-Claro y TD-Learning.
Vamos a hablar de la Ecuación de Bellman con mucho más detalle en la siguiente historia.
¿Qué es el Proceso de Decisión de Markov?
Proceso de Decisión de Markov : Es un Proceso de Recompensa de Markov con una decisión.Todo es igual que el MRP pero ahora tenemos una agencia real que toma decisiones o acciones.
Es una tupla de (S, A, P, R, 𝛾) donde:
- S es un conjunto de estados,
- A es el conjunto de acciones que el agente puede elegir tomar,
- P es la Matriz de Probabilidad de transición,
- R es la Recompensa acumulada por las acciones del agente,
- 𝛾 es el factor de descuento.
P y R tendrán un ligero cambio w.r.t acciones como sigue :
Matriz de Probabilidad de Transición
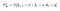
Función de Recompensa
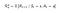
Ahora, nuestra función de recompensa depende de la acción.
Hasta ahora hemos hablado de obtener una recompensa (r) cuando nuestro agente pasa por un conjunto de estados (s) siguiendo una política π.En realidad, en un Proceso de Decisión de Markov (MDP) la política es el mecanismo para tomar decisiones.Así que ahora tenemos un mecanismo que elegirá tomar una acción.
Las políticas en un MDP dependen del estado actual.No dependen de la historia.Esa es la propiedad de Markov.Así, el estado actual en el que estamos caracteriza la historia.
Ya hemos visto lo bueno que es para el agente estar en un estado particular(Función Estado-Valor).Ahora, vamos a ver lo bueno que es tomar una acción particular siguiendo una política π desde el estado s (Función Acción-Valor).
Función Estado-Valor Acción o Función Q
Esta función especifica lo bueno que es para el agente tomar una acción (a) en un estado (s) con una política π.
Matemáticamente, podemos definir la función de valor Estado-acción como :

Básicamente, nos dice el valor de realizar una determinada acción(a) en un estado(s) con una política π.
Veamos un ejemplo de Proceso de Decisión de Markov :
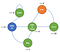
Ahora, podemos ver que no hay más probabilidades.De hecho, ahora nuestro agente tiene opciones para hacer como después de despertar, podemos elegir para ver Netflix o el código y la depuración.Por supuesto, las acciones del agente se definen w.r.t alguna política π y será obtener la recompensa en consecuencia.