
Aunque, como se menciona en la sección Análisis de flujo de señales, alguna forma de análisis de flujo de señales es la manera más general de tratar el amplificador de retroalimentación negativa, la representación como dos dos puertos es el enfoque que se presenta con más frecuencia en los libros de texto y se presenta aquí. Conserva una partición del circuito de dos bloques del amplificador, pero permite que los bloques sean bilaterales. Al final se describen algunos inconvenientes de este método.
Los amplificadores electrónicos utilizan corriente o tensión como entrada y salida, por lo que son posibles cuatro tipos de amplificadores (cualquiera de dos posibles entradas con cualquiera de dos posibles salidas). Véase la clasificación de los amplificadores. El objetivo del amplificador de realimentación puede ser cualquiera de los cuatro tipos de amplificador y no es necesariamente el mismo tipo que el amplificador de bucle abierto, que a su vez puede ser cualquiera de estos tipos. Así, por ejemplo, un amplificador óptico (amplificador de tensión) puede disponerse para hacer un amplificador de corriente en su lugar.
Los amplificadores de retroalimentación negativa de cualquier tipo pueden implementarse utilizando combinaciones de redes de dos puertos. Hay cuatro tipos de redes de dos puertos, y el tipo de amplificador deseado dicta la elección de dos puertos y la selección de una de las cuatro topologías de conexión diferentes que se muestran en el diagrama. Estas conexiones suelen denominarse conexiones en serie o en derivación (en paralelo). En el diagrama, la columna de la izquierda muestra las entradas en derivación; la de la derecha, las entradas en serie. La fila superior muestra las salidas en serie; la fila inferior, las salidas en derivación. Las diferentes combinaciones de conexiones y dos puertos se enumeran en la tabla siguiente.
| Tipo de amplificador de retroalimentación | Conexión de entrada | Conexión de salida | Retroalimentación ideal | Dosretroalimentación |
|---|---|---|---|---|
| Corriente | Remisión | Serie | CCCS | |
| Transresistencia | Remisión | CCVS | y-parámetro | |
| Transconductancia | Serie | VCCS | ||
| Tensión | Serie | Shunt | VCVS |
Por ejemplo, para un amplificador de retroalimentación de corriente, la corriente de la salida se muestrea para la retroalimentación y se combina con la corriente en la entrada. Por lo tanto, la realimentación se realiza idealmente utilizando una fuente de corriente (de salida) controlada por corriente (CCCS), y su realización imperfecta utilizando una red de dos puertos también debe incorporar una CCCS, es decir, la elección apropiada para la red de realimentación es una de dos puertos de parámetro g. Aquí se presenta el método de dos puertos utilizado en la mayoría de los libros de texto, utilizando el circuito tratado en el artículo sobre el modelo de ganancia asintótica.

La figura 3 muestra un amplificador de dos transistores con una resistencia de realimentación Rf. El objetivo es analizar este circuito para encontrar tres elementos: la ganancia, la impedancia de salida mirando al amplificador desde la carga y la impedancia de entrada mirando al amplificador desde la fuente.
- Sustitución de la red de realimentación por una de dos puertosEditar
- Circuito de pequeña señalEditar
- Ganancia de lazo abierto cargadoEditar
- Ganancia con realimentaciónEditar
- Resistencias de entrada y salidaEditar
- Antecedentes de la determinación de la resistenciaEditar
- Aplicación al amplificador de ejemploEditar
- Tensión de carga y corriente de cargaEditar
- ¿Es el bloque amplificador principal de dos puertos?
Sustitución de la red de realimentación por una de dos puertosEditar
El primer paso es la sustitución de la red de realimentación por una de dos puertos. ¿Qué componentes van en la red de dos puertos?
En el lado de entrada de la red de dos puertos tenemos Rf. Si la tensión en el lado derecho de Rf cambia, cambia la corriente en Rf que se resta de la corriente que entra en la base del transistor de entrada. Es decir, el lado de entrada de los dos puertos es una fuente de corriente dependiente controlada por la tensión en la parte superior de la resistencia R2.
Se podría decir que la segunda etapa del amplificador es sólo un seguidor de tensión, transmitiendo la tensión en el colector del transistor de entrada a la parte superior de R2. Es decir, la señal de salida controlada es realmente la tensión en el colector del transistor de entrada. Este punto de vista es legítimo, pero entonces la etapa seguidora de tensión se convierte en parte de la red de realimentación. Esto hace que el análisis de la realimentación sea más complicado.
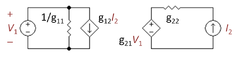
Un punto de vista alternativo es que la tensión en la parte superior de R2 es fijada por la corriente del emisor del transistor de salida. Este punto de vista conduce a una red de realimentación totalmente pasiva formada por R2 y Rf. La variable que controla la realimentación es la corriente de emisor, por lo que la realimentación es una fuente de corriente controlada por corriente (CCCS). Buscamos entre las cuatro redes de dos puertos disponibles y encontramos que la única con una CCCS es la de dos puertos con parámetro g, mostrada en la Figura 4. La siguiente tarea es seleccionar los parámetros g para que el dos puertos de la figura 4 sea eléctricamente equivalente a la sección L formada por R2 y Rf. Esta selección es un procedimiento algebraico que se realiza de forma muy sencilla observando dos casos individuales: el caso con V1 = 0, que hace que el VCVS del lado derecho del puerto doble sea un cortocircuito; y el caso con I2 = 0, que hace que el CCCS del lado izquierdo sea un circuito abierto. El álgebra en estos dos casos es sencilla, mucho más fácil que resolver para todas las variables a la vez. La elección de los parámetros g que hacen que la sección de dos puertos y la sección L se comporten de la misma manera se muestran en la siguiente tabla.
| g11 | g12 | g21 | g22 |
|---|---|---|---|
1 R f + R 2 {\displaystyle {\frac {1}{R_{mathrm {f}} }+R_{2}}}}
 |
– R 2 R 2 + R f {{displaystyle -{{frac {R_{2}}{R_{2}+R_{mathrm {f}} }}}}
 |
R 2 R 2 + R f {\displaystyle {\frac {R_{2}}{R_{2}+R_{mathrm {f} }}}}
 |
R 2 / / R f {\displaystyle R_{2}//R_{mathrm {f} }\ }
 |
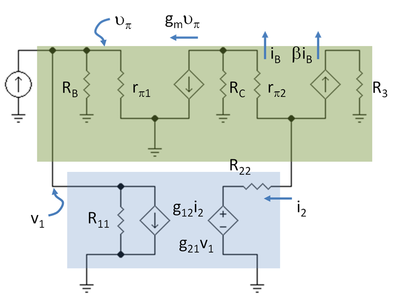
Circuito de pequeña señalEditar
El siguiente paso es dibujar el esquema de pequeña señal para el amplificador con el dos puertos en su lugar utilizando el modelo híbrido-pi para los transistores. La figura 5 muestra el esquema con la notación R3 = RC2 // RL y R11 = 1 / g11, R22 = g22.
Ganancia de lazo abierto cargadoEditar
La figura 3 indica el nodo de salida, pero no la elección de la variable de salida. Una elección útil es la salida de corriente de cortocircuito del amplificador (que conduce a la ganancia de corriente de cortocircuito). Debido a que esta variable conduce simplemente a cualquiera de las otras opciones (por ejemplo, la tensión de carga o la corriente de carga), la ganancia de corriente de cortocircuito se encuentra a continuación.
Primero se encuentra la ganancia de lazo abierto cargado. La retroalimentación se desactiva estableciendo g12 = g21 = 0. La idea es encontrar cuánto cambia la ganancia del amplificador debido a las resistencias en la red de retroalimentación por sí mismas, con la retroalimentación desactivada. Este cálculo es bastante fácil porque R11, RB y rπ1 están todos en paralelo y v1 = vπ. Sea R1 = R11 // RB // rπ1. Además, i2 = -(β+1) iB. El resultado para la ganancia de corriente en lazo abierto AOL es:
A O L = β i B i S = g m R C ( β β + 1 ) ( R 1 R 22 + r π 2 + R C β + 1 ) . {\displaystyle A_{{mathrm {OL}} }={frac {\beta i_{mathrm {B}} }}{i_{mathrm}{S}} R_{mathrm}{c}que es la que se encuentra en la parte inferior de la pantalla. izquierda({\frac {\beta }{beta +1}}derecha)\frac({R_{1}}{R_{22}}+{\frac {r_{pi 2}+R_{mathrm {C}}{{\bita +1}} {\beta +1}}}}\\right)\N-.}

Ganancia con realimentaciónEditar
En el enfoque clásico de la realimentación, se desprecia el feedforward representado por el VCVS (es decir, g21 v1). Eso hace que el circuito de la figura 5 se parezca al diagrama de bloques de la figura 1, y la ganancia con realimentación es entonces:
A F B = A O L 1 + β F B A O L {\displaystyle A_{{mathrm {FB}} }={frac {A_{mathrm {OL}} {1+{{beta}} {{mathrm {FB}} A_{mathrm} {OL} }}}}

A F B = A O L 1 + R 2 R 2 + R f A O L , {\displaystyle A_{{mathrm {FB} }={\\frac {A O L} }={frac {A_{mathrm {OL}} {1+{frac {R_{2}}{R_{2}+R_{mathrm {f}} A_{mathrm {OL}}
Resistencias de entrada y salidaEditar

La realimentación se utiliza para adaptar mejor las fuentes de señal a sus cargas. Por ejemplo, una conexión directa de una fuente de tensión a una carga resistiva puede dar lugar a una pérdida de señal debido a la división de la tensión, pero intercalar un amplificador de realimentación negativa puede aumentar la carga aparente vista por la fuente, y reducir la impedancia aparente del conductor vista por la carga, evitando la atenuación de la señal por la división de la tensión. Esta ventaja no se limita a los amplificadores de tensión, sino que se pueden conseguir mejoras análogas en la adaptación para los amplificadores de corriente, los amplificadores de transconductancia y los amplificadores de transresistencia.
Para explicar estos efectos de la realimentación sobre las impedancias, primero hay que hacer una digresión sobre cómo la teoría de dos puertos aborda la determinación de la resistencia, y luego su aplicación al amplificador que nos ocupa.
Antecedentes de la determinación de la resistenciaEditar
La figura 6 muestra un circuito equivalente para encontrar la resistencia de entrada de un amplificador de tensión realimentado (izquierda) y para un amplificador de corriente realimentado (derecha). Estas disposiciones son aplicaciones típicas del teorema de Miller.
En el caso del amplificador de tensión, la tensión de salida βVout de la red de realimentación se aplica en serie y con una polaridad opuesta a la tensión de entrada Vx que recorre el bucle (pero respecto a tierra, las polaridades son las mismas). Como resultado, la tensión efectiva a través y la corriente a través de la resistencia de entrada del amplificador Rin disminuyen de manera que la resistencia de entrada del circuito aumenta (se podría decir que Rin aparentemente aumenta). Su nuevo valor puede calcularse aplicando el teorema de Miller (para las tensiones) o las leyes básicas del circuito. Así, la ley de tensión de Kirchhoff proporciona:
V x = I x R i n + β v o u t , {\displaystyle V_{x}=I_{x}R_{\mathrm {in} v_{{mathrm {out}}, +beta v_{mathrm {out}}

donde vout = Av vin = Av Ix Rin. Sustituyendo este resultado en la ecuación anterior y resolviendo para la resistencia de entrada del amplificador de realimentación, el resultado es:
R i n ( f b ) = V x I x = ( 1 + β A v ) R i n . {\displaystyle R_{mathrm {in} }(fb)={frac {V_{x}}{I_{x}}={left(1+\beta A_{v}{right)} R_{mathrm {in}} }\ .}

La conclusión general de este ejemplo y de un ejemplo similar para el caso de la resistencia de salida es:Una conexión de realimentación en serie en la entrada (salida) aumenta la resistencia de entrada (salida) en un factor ( 1 + β AOL ), donde AOL = ganancia de bucle abierto.
Por otro lado, para el amplificador de corriente, la corriente de salida βIout de la red de realimentación se aplica en paralelo y con sentido contrario a la corriente de entrada Ix. Como resultado, la corriente total que fluye a través de la entrada del circuito (no sólo a través de la resistencia de entrada Rin) aumenta y la tensión a través de ella disminuye, de modo que la resistencia de entrada del circuito disminuye (Rin aparentemente disminuye). Su nuevo valor se puede calcular aplicando el teorema dual de Miller (para corrientes) o las leyes básicas de Kirchhoff:
I x = V i n R i n + β i o u t . {\displaystyle I_{x}={frac {V_{mathrm {in} R_{mathrm{in}} {}+\\a i_{mathrm {out}} }\ .}

donde iout = Ai iin = Ai Vx / Rin. Sustituyendo este resultado en la ecuación anterior y resolviendo para la resistencia de entrada del amplificador de realimentación, el resultado es:
R i n ( f b ) = V x I x = R i n ( 1 + β A i ) . {\displaystyle R_{mathrm {in} }(fb)={frac {V_{x}}{I_{x}}={frac {R_{mathrm {in}} izquierda(1+beta A_{i}dcha)}}.

La conclusión general de este ejemplo y de un ejemplo similar para el caso de la resistencia de salida es:Una conexión de realimentación en paralelo en la entrada (salida) disminuye la resistencia de entrada (salida) en un factor ( 1 + β AOL ), donde AOL = ganancia de bucle abierto.
Estas conclusiones se pueden generalizar para tratar casos con accionamientos arbitrarios de Norton o Thévenin, cargas arbitrarias y redes generales de realimentación de dos puertos. Sin embargo, los resultados dependen de que el amplificador principal tenga una representación como de dos puertos – es decir, los resultados dependen de que la misma corriente entre y salga de los terminales de entrada, y del mismo modo, la misma corriente que sale de un terminal de salida debe entrar en el otro terminal de salida.
Una conclusión más amplia, independiente de los detalles cuantitativos, es que la realimentación puede utilizarse para aumentar o disminuir la impedancia de entrada y de salida.
Aplicación al amplificador de ejemploEditar
Estos resultados de resistencia se aplican ahora al amplificador de la figura 3 y la figura 5. El factor de mejora que reduce la ganancia, a saber ( 1 + βFB AOL), decide directamente el efecto de la realimentación sobre las resistencias de entrada y salida del amplificador. En el caso de una conexión en derivación, la impedancia de entrada se reduce por este factor; y en el caso de una conexión en serie, la impedancia se multiplica por este factor. Sin embargo, la impedancia modificada por la realimentación es la del amplificador de la figura 5 con la realimentación desactivada, e incluye las modificaciones de la impedancia causadas por las resistencias de la red de realimentación.
Por tanto, la impedancia de entrada vista por la fuente con la realimentación desactivada es Rin = R1 = R11 // RB // rπ1, y con la realimentación activada (pero sin feedforward)
R i n = R 1 1 + β F B A O L , {\displaystyle R_{mathrm {in} }={frac {R_1}{1+{mathrm {FB}}. }={\frac {R_{1}}{1+{\beta }_{\mathrm {FB}}} A_{mathrm {OL}}, que es lo que se conoce como

donde la división se utiliza porque la conexión de entrada es en derivación: la realimentación de dos puertos está en paralelo con la fuente de señal en el lado de entrada del amplificador. Un recordatorio: AOL es la ganancia de bucle abierto con carga encontrada anteriormente, modificada por las resistencias de la red de realimentación.
La impedancia vista por la carga necesita más discusión. La carga en la Figura 5 está conectada al colector del transistor de salida, y por lo tanto está separada del cuerpo del amplificador por la impedancia infinita de la fuente de corriente de salida. Por lo tanto, la realimentación no tiene ningún efecto sobre la impedancia de salida, que sigue siendo simplemente RC2 como se ve por la resistencia de carga RL en la figura 3.
Si en cambio quisiéramos encontrar la impedancia que se presenta en el emisor del transistor de salida (en lugar de su colector), que está conectado en serie a la red de realimentación, la realimentación aumentaría esta resistencia por el factor de mejora ( 1 + βFB AOL).
Tensión de carga y corriente de cargaEditar
La ganancia derivada anteriormente es la ganancia de corriente en el colector del transistor de salida. Para relacionar esta ganancia con la ganancia cuando la tensión es la salida del amplificador, observe que la tensión de salida en la carga RL está relacionada con la corriente de colector por la ley de Ohm como vL = iC (RC2 || RL). En consecuencia, la ganancia de transresistencia vL / iS se encuentra multiplicando la ganancia de corriente por RC2 | RL:
v L i S = A F B ( R C 2 ∥ R L ) . {\displaystyle {\frac {v_{mathrm {L}} }}{i_{mathrm {S}} }}=A_{mathrm {FB}} (R_{mathrm {C2} }paralelo R_{mathrm {L} })}.

De forma similar, si se toma la salida del amplificador como la corriente en la resistencia de carga RL, la división de la corriente determina la corriente de carga, y la ganancia es entonces:
i L i S = A F B R C 2 R C 2 + R L . { {{mathrm }}} y S. { {{mathrm {FB}}=A_{mathrm {FB}}. {{frac}} R_{mathrm}{C2}} R_{mathrm {C2} }} y R_{mathrm {C2}}. + R_{mathrm {L}} y el resto de la gente. }}}\ .}

¿Es el bloque amplificador principal de dos puertos?

A continuación se presentan algunos inconvenientes del enfoque de dos puertos, destinados al lector atento.
La figura 7 muestra el esquema de pequeña señal con el amplificador principal y el de dos puertos de realimentación en recuadros sombreados. El bipuerto de realimentación satisface las condiciones de puerto: en el puerto de entrada, Iin entra y sale del puerto, e igualmente en la salida, Iout entra y sale.
¿Es el bloque del amplificador principal también un bipuerto? El amplificador principal se muestra en el cuadro superior sombreado. Las conexiones a tierra están etiquetadas. La figura 7 muestra el hecho interesante de que el amplificador principal no satisface las condiciones de puerto en su entrada y salida a menos que las conexiones a tierra se elijan para que eso ocurra. Por ejemplo, en el lado de entrada, la corriente que entra en el amplificador principal es IS. Esta corriente se divide de tres maneras: a la red de realimentación, a la resistencia de polarización RB y a la resistencia de base del transistor de entrada rπ. Para satisfacer la condición de puerto para el amplificador principal, los tres componentes deben ser devueltos al lado de entrada del amplificador principal, lo que significa que todos los cables de tierra etiquetados como G1 deben estar conectados, así como el cable de emisor GE1. Del mismo modo, en el lado de salida, deben conectarse todas las conexiones a tierra G2 y también la conexión a tierra GE2. Entonces, en la parte inferior del esquema, debajo de la retroalimentación de dos puertos y fuera de los bloques del amplificador, G1 se conecta a G2. Esto obliga a que las corrientes de tierra se dividan entre los lados de entrada y de salida, tal y como estaba previsto. Observe que esta disposición de las conexiones divide el emisor del transistor de entrada en un lado de la base y un lado del colector – algo físicamente imposible de hacer, pero eléctricamente el circuito ve todas las conexiones a tierra como un nodo, por lo que se permite esta ficción.
Por supuesto, la forma en que se conectan los cables de tierra no hace ninguna diferencia para el amplificador (todos son un nodo), pero hace una diferencia en las condiciones del puerto. Esta artificialidad es una debilidad de este enfoque: las condiciones de puerto son necesarias para justificar el método, pero el circuito realmente no se ve afectado por cómo se intercambian las corrientes entre las conexiones de tierra.
Sin embargo, si ninguna disposición posible de las condiciones de tierra conduce a las condiciones de puerto, el circuito podría no comportarse de la misma manera. Los factores de mejora (1 + βFB AOL) para determinar la impedancia de entrada y salida podrían no funcionar. Esta situación es incómoda, porque el hecho de no hacer un puerto doble puede reflejar un problema real (simplemente no es posible), o reflejar una falta de imaginación (por ejemplo, simplemente no se pensó en dividir el nodo emisor en dos). En consecuencia, cuando las condiciones del puerto son dudosas, son posibles al menos dos enfoques para establecer si los factores de mejora son precisos: o bien simular un ejemplo usando Spice y comparar los resultados con el uso de un factor de mejora, o calcular la impedancia usando una fuente de prueba y comparar los resultados.
Una opción más práctica es dejar de lado el enfoque de dos puertos por completo, y utilizar varias alternativas basadas en la teoría de los gráficos de flujo de señales, incluyendo el método de Rosenstark, el método de Choma, y el uso del teorema de Blackman. Esta opción puede ser aconsejable si los modelos de dispositivos de pequeña señal son complejos, o no están disponibles (por ejemplo, los dispositivos se conocen sólo numéricamente, tal vez a partir de mediciones o de simulaciones SPICE).