
Obwohl, wie im Abschnitt Signalflussanalyse erwähnt, eine Form der Signalflussanalyse die allgemeinste Art ist, den Gegenkopplungsverstärker zu behandeln, ist die Darstellung als zwei Zweitore der in Lehrbüchern am häufigsten vorgestellte Ansatz und wird hier vorgestellt. Dabei wird die Aufteilung des Verstärkers in zwei Blöcke beibehalten, die Blöcke können aber auch zweiseitig sein. Einige Nachteile dieser Methode werden am Ende beschrieben.
Elektronische Verstärker verwenden Strom oder Spannung als Eingang und Ausgang, so dass vier Arten von Verstärkern möglich sind (jeder von zwei möglichen Eingängen mit jedem von zwei möglichen Ausgängen). Siehe Klassifizierung von Verstärkern. Das Ziel des rückgekoppelten Verstärkers kann ein beliebiger der vier Verstärkertypen sein und ist nicht unbedingt derselbe Typ wie der Open-Loop-Verstärker, der seinerseits ein beliebiger dieser Typen sein kann. So kann z. B. ein Operationsverstärker (Spannungsverstärker) so angeordnet werden, dass er stattdessen einen Stromverstärker bildet.
Verstärker mit negativer Rückkopplung jeder Art können durch Kombinationen von Netzwerken mit zwei Anschlüssen realisiert werden. Es gibt vier Arten von Zweitor-Netzwerken, und der gewünschte Verstärkertyp diktiert die Wahl der Zweitore und die Auswahl einer der vier verschiedenen Verbindungstopologien, die im Diagramm dargestellt sind. Diese Verbindungen werden in der Regel als Reihen- oder Nebenschlussverbindungen (parallel) bezeichnet. Im Diagramm zeigt die linke Spalte die Shunt-Eingänge, die rechte Spalte die Serien-Eingänge. Die obere Reihe zeigt die Serienausgänge, die untere Reihe die Shunt-Ausgänge. Die verschiedenen Kombinationen von Anschlüssen und Zweiports sind in der nachstehenden Tabelle aufgeführt.
| Rückkopplungsverstärkertyp | Eingangsanschluss | Ausgangsanschluss | Ideale Rückkopplung | Zwei-Anschluss-Rückführung |
|---|---|---|---|---|
| Strom | Shunt | Serie | CCCS | g-Parameter |
| Transistanzwiderstand | Shunt | Shunt | CCVS | y-Parameter |
| Transkonduktanz | Serie | Serie | VCCS | z-Parameter |
| Spannung | Serie | Shunt | VCVVS | h-Parameter |
Zum Beispiel, Bei einem stromrückgekoppelten Verstärker wird der Strom am Ausgang zur Rückkopplung abgetastet und mit dem Strom am Eingang kombiniert. Daher erfolgt die Rückkopplung idealerweise mit einer (ausgangs-)stromgesteuerten Stromquelle (CCCS), und ihre unvollkommene Realisierung mit einem Zweitor-Netzwerk muss ebenfalls ein CCCS enthalten, d. h. die geeignete Wahl für das Rückkopplungsnetzwerk ist ein g-Parameter-Zweitor. Hier wird die in den meisten Lehrbüchern verwendete Zweitor-Methode anhand der im Artikel über das asymptotische Verstärkungsmodell behandelten Schaltung vorgestellt.

Abbildung 3 zeigt einen Verstärker mit zwei Transistoren und einem Rückkopplungswiderstand Rf. Ziel ist es, diese Schaltung zu analysieren, um drei Größen zu ermitteln: die Verstärkung, die Ausgangsimpedanz, wenn man von der Last aus in den Verstärker schaut, und die Eingangsimpedanz, wenn man von der Quelle aus in den Verstärker schaut.
- Ersetzen des Rückkopplungsnetzwerks durch ein ZweipolEdit
- KleinsignalschaltungBearbeiten
- Geladene Open-Loop-VerstärkungBearbeiten
- Verstärkung mit RückkopplungBearbeiten
- Eingangs- und AusgangswiderständeBearbeiten
- Hintergrund zur WiderstandsermittlungBearbeiten
- Anwendung auf den BeispielverstärkerBearbeiten
- Lastspannung und LaststromEdit
- Ist der Hauptverstärkerblock ein Zweitor?Edit
Ersetzen des Rückkopplungsnetzwerks durch ein ZweipolEdit
Der erste Schritt ist das Ersetzen des Rückkopplungsnetzwerks durch ein Zweipol. Welche Komponenten sind in dem Zweitor enthalten?
Auf der Eingangsseite des Zweitors haben wir Rf. Wenn sich die Spannung auf der rechten Seite von Rf ändert, ändert sich der Strom in Rf, der von dem Strom, der in die Basis des Eingangstransistors fließt, abgezogen wird. Das heißt, die Eingangsseite des Zweitors ist eine abhängige Stromquelle, die von der Spannung am oberen Ende des Widerstands R2 gesteuert wird.
Man könnte sagen, dass die zweite Stufe des Verstärkers nur ein Spannungsfolger ist, der die Spannung am Kollektor des Eingangstransistors an das obere Ende von R2 überträgt. Das heißt, das überwachte Ausgangssignal ist in Wirklichkeit die Spannung am Kollektor des Eingangstransistors. Diese Ansicht ist legitim, aber dann wird die Spannungsfolgestufe Teil des Rückkopplungsnetzwerks. Das macht die Analyse der Rückkopplung komplizierter.
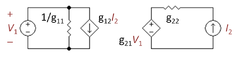
Eine alternative Sichtweise ist, dass die Spannung an der Spitze von R2 durch den Emitterstrom des Ausgangstransistors eingestellt wird. Diese Sichtweise führt zu einem vollständig passiven Rückkopplungsnetzwerk, das aus R2 und Rf besteht. Die Variable, die die Rückkopplung steuert, ist der Emitterstrom, also ist die Rückkopplung eine stromgesteuerte Stromquelle (CCCS). Wir durchsuchen die vier verfügbaren Zweitor-Netzwerke und finden das einzige mit einer CCCS, nämlich das g-Parameter-Zweitor-Netzwerk, das in Abbildung 4 dargestellt ist. Die nächste Aufgabe besteht darin, die g-Parameter so zu wählen, dass das Zweitor in Abbildung 4 elektrisch äquivalent zum L-Teil ist, der aus R2 und Rf besteht. Diese Auswahl ist eine algebraische Prozedur, die am einfachsten durch die Betrachtung von zwei Einzelfällen erfolgt: der Fall mit V1 = 0, der den VCVS auf der rechten Seite des Zweitors zu einem Kurzschluss macht; und der Fall mit I2 = 0, der den CCCS auf der linken Seite zu einem offenen Stromkreis macht. Die Algebra in diesen beiden Fällen ist einfach, viel einfacher als die Lösung für alle Variablen auf einmal. Die Wahl der g-Parameter, die dazu führen, dass sich der Zweitor- und der L-Teil gleich verhalten, ist in der folgenden Tabelle dargestellt.
| g11 | g12 | g21 | g22 |
|---|---|---|---|
1 R f + R 2 {\displaystyle {\frac {1}{R_{\mathrm {f} }+R_{2}}}}
 |
– R 2 R 2 + R f {\displaystyle -{\frac {R_{2}}{R_{2}+R_{\mathrm {f} }}}}
 |
R 2 R 2 + R f {\displaystyle {\frac {R_{2}}{R_{2}+R_{\mathrm {f} }}}}
 |
R 2 / / R f {\displaystyle R_{2}//R_{\mathrm {f} }\ }
 |
KleinsignalschaltungBearbeiten
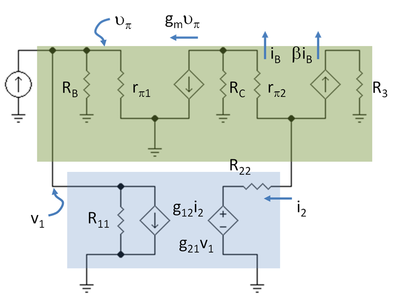
Der nächste Schritt besteht darin, das Kleinsignalschaltbild für den Verstärker mit dem Zweitor zu zeichnen, indem das Hybrid-Pi-Modell für die Transistoren verwendet wird. Abbildung 5 zeigt das Schaltbild mit der Notation R3 = RC2 // RL und R11 = 1 / g11, R22 = g22.
Geladene Open-Loop-VerstärkungBearbeiten
Abbildung 3 zeigt den Ausgangsknoten, aber nicht die Wahl der Ausgangsgröße. Eine sinnvolle Wahl ist der Kurzschlussstromausgang des Verstärkers (was zur Kurzschlussstromverstärkung führt). Da diese Variable einfach zu einer der anderen Auswahlmöglichkeiten führt (z. B. Lastspannung oder Laststrom), wird die Kurzschlussstromverstärkung weiter unten gefunden.
Zuerst wird die geladene Open-Loop-Verstärkung gefunden. Die Rückkopplung wird ausgeschaltet, indem g12 = g21 = 0 gesetzt wird. Es geht darum, herauszufinden, wie stark sich die Verstärkung des Verstärkers durch die Widerstände im Rückkopplungsnetzwerk selbst bei ausgeschalteter Rückkopplung ändert. Diese Berechnung ist recht einfach, da R11, RB und rπ1 alle parallel geschaltet sind und v1 = vπ. Es sei R1 = R11 // RB // rπ1. Außerdem gilt: i2 = -(β+1) iB. Das Ergebnis für die Leerlaufstromverstärkung AOL ist:
A O L = β i B i S = g m R C ( β β + 1 ) ( R 1 R 22 + r π 2 + R C β + 1 ) . {\displaystyle A_{\mathrm {OL} }={\frac {\beta i_{\mathrm {B} }}{i_{\mathrm {S} }}}=g_{m}R_{\mathrm {C} }\left({\frac {\beta }{\beta +1}}\right)\left({\frac {R_{1}}{R_{22}+{\frac {r_{\pi 2}+R_{\mathrm {C} }}{\beta +1}}}}\right)\ .}

Verstärkung mit RückkopplungBearbeiten
Beim klassischen Ansatz der Rückkopplung wird die durch die VCVS dargestellte Vorwärtskopplung (d.h. g21 v1) vernachlässigt. Damit ähnelt die Schaltung von Abbildung 5 dem Blockdiagramm von Abbildung 1, und die Verstärkung mit Rückkopplung ist dann:
A F B = A O L 1 + β F B A O L {\displaystyle A_{\mathrm {FB} }={\frac {A_{\mathrm {OL} }}{1+{\beta }_{\mathrm {FB} }A_{\mathrm {OL} }}}}

A F B = A O L 1 + R 2 R 2 + R f A O L , {\displaystyle A_{\mathrm {FB} }={\frac {A_{\mathrm {OL} }}{1+{\frac {R_{2}}{R_{2}+R_{\mathrm {f} }}}A_{\mathrm {OL} }}} ,}

wobei der Rückkopplungsfaktor βFB = -g12. Die Schreibweise βFB wird für den Rückkopplungsfaktor eingeführt, um ihn vom Transistor β zu unterscheiden.
Eingangs- und AusgangswiderständeBearbeiten

Rückkopplung wird verwendet, um Signalquellen besser an ihre Lasten anzupassen. So kann beispielsweise der direkte Anschluss einer Spannungsquelle an eine ohmsche Last zu einem Signalverlust aufgrund der Spannungsteilung führen, während die Einschaltung eines Gegenkopplungsverstärkers die scheinbare Last, die von der Quelle gesehen wird, erhöhen und die scheinbare Treiberimpedanz, die von der Last gesehen wird, verringern kann, wodurch eine Signaldämpfung durch Spannungsteilung vermieden wird. Dieser Vorteil ist nicht auf Spannungsverstärker beschränkt, sondern analoge Anpassungsverbesserungen können auch für Stromverstärker, Transkonduktanzverstärker und Transwiderstandsverstärker erzielt werden.
Um diese Auswirkungen der Rückkopplung auf die Impedanzen zu erklären, ist zunächst ein Exkurs darüber erforderlich, wie die Zwei-Tor-Theorie bei der Bestimmung des Widerstands vorgeht, und dann ihre Anwendung auf den vorliegenden Verstärker.
Hintergrund zur WiderstandsermittlungBearbeiten
Abbildung 6 zeigt eine Ersatzschaltung zur Ermittlung des Eingangswiderstandes eines rückgekoppelten Spannungsverstärkers (links) und für einen rückgekoppelten Stromverstärker (rechts). Diese Anordnungen sind typische Anwendungen des Miller-Theorems.
Im Falle des Spannungsverstärkers liegt die Ausgangsspannung βVout des Rückkopplungsnetzwerks in Reihe und mit entgegengesetzter Polarität zur Eingangsspannung Vx, die über die Schleife läuft, an (in Bezug auf die Masse sind die Polaritäten jedoch gleich). Infolgedessen sinken die effektive Spannung am und der Strom durch den Verstärkereingangswiderstand Rin, so dass der Eingangswiderstand der Schaltung zunimmt (man könnte sagen, dass Rin scheinbar zunimmt). Sein neuer Wert kann mit Hilfe des Miller-Theorems (für Spannungen) oder der grundlegenden Schaltungsgesetze berechnet werden. So besagt das Kirchhoffsche Spannungsgesetz:
V x = I x R i n + β v o u t , {\displaystyle V_{x}=I_{x}R_{\mathrm {in} }+beta v_{\mathrm {out} } ,}

wobei vout = Av vin = Av Ix Rin. Setzt man dieses Ergebnis in die obige Gleichung ein und löst den Eingangswiderstand des rückgekoppelten Verstärkers auf, so erhält man:
R i n ( f b ) = V x I x = ( 1 + β A v ) R i n . {R {\displaystyle R_{\mathrm} }(fb)={\frac {V_{x}}{I_{x}}}=\left(1+\beta A_{v}\right)R_{\mathrm {in} }\ .}

Die allgemeine Schlussfolgerung aus diesem Beispiel und einem ähnlichen Beispiel für den Fall des Ausgangswiderstandes lautet: Eine Reihenschaltung der Rückkopplung am Eingang (Ausgang) erhöht den Eingangs- (Ausgangs-) Widerstand um den Faktor ( 1 + β AOL ), wobei AOL = Verstärkung der offenen Schleife ist.
Beim Stromverstärker hingegen wird der Ausgangsstrom βIout des Rückkopplungsnetzwerks parallel und mit entgegengesetzter Richtung zum Eingangsstrom Ix angelegt. Infolgedessen steigt der Gesamtstrom, der durch den Eingang der Schaltung fließt (nicht nur durch den Eingangswiderstand Rin), und die Spannung an ihm sinkt, so dass der Eingangswiderstand der Schaltung sinkt (Rin nimmt offensichtlich ab). Sein neuer Wert kann durch Anwendung des dualen Miller-Theorems (für Ströme) oder der grundlegenden Kirchhoffschen Gesetze berechnet werden:
I x = V i n R i n + β i o u t . {\displaystyle I_{x}={\frac {V_{\mathrm {in} }}{R_{\mathrm {in} }}+\beta i_{\mathrm {out} }\ .}

wobei iout = Ai iin = Ai Vx / Rin. Setzt man dieses Ergebnis in die obige Gleichung ein und löst den Eingangswiderstand des rückgekoppelten Verstärkers auf, so erhält man:
R i n ( f b ) = V x I x = R i n ( 1 + β A i ) . {\displaystyle R_{\mathrm {in} }(fb)={\frac {V_{x}}{I_{x}}}={\frac {R_{\mathrm {in} }}{\left(1+\beta A_{i}\right)}}.}

Die allgemeine Schlussfolgerung aus diesem Beispiel und einem ähnlichen Beispiel für den Fall des Ausgangswiderstandes lautet: Eine parallele Rückkopplung am Eingang (Ausgang) verringert den Eingangs- (Ausgangs-) Widerstand um einen Faktor ( 1 + β AOL ), wobei AOL = Verstärkung der offenen Schleife.
Diese Schlussfolgerungen können verallgemeinert werden, um Fälle mit beliebigen Norton- oder Thévenin-Antrieben, beliebigen Lasten und allgemeinen Rückkopplungsnetzwerken mit zwei Anschlüssen zu behandeln. Die Ergebnisse hängen jedoch davon ab, dass der Hauptverstärker als Zweitor dargestellt wird – das heißt, die Ergebnisse hängen davon ab, dass an den Eingangsklemmen derselbe Strom ein- und ausgeht, und ebenso muss derselbe Strom, der eine Ausgangsklemme verlässt, an der anderen Ausgangsklemme eintreten.
Eine allgemeinere Schlussfolgerung, unabhängig von den quantitativen Details, ist, dass die Rückkopplung verwendet werden kann, um die Eingangs- und Ausgangsimpedanz zu erhöhen oder zu verringern.
Anwendung auf den BeispielverstärkerBearbeiten
Diese Widerstandsergebnisse werden nun auf den Verstärker von Abbildung 3 und Abbildung 5 angewendet. Der Verbesserungsfaktor, der die Verstärkung reduziert, nämlich ( 1 + βFB AOL), entscheidet direkt über die Wirkung der Rückkopplung auf den Eingangs- und Ausgangswiderstand des Verstärkers. Im Falle einer Nebenschlussschaltung wird die Eingangsimpedanz um diesen Faktor verringert, und im Falle einer Reihenschaltung wird die Impedanz mit diesem Faktor multipliziert. Die Impedanz, die durch die Rückkopplung verändert wird, ist jedoch die Impedanz des Verstärkers in Abbildung 5 bei ausgeschalteter Rückkopplung und schließt die durch die Widerstände des Rückkopplungsnetzwerks verursachten Impedanzänderungen ein.
Daher ist die Eingangsimpedanz, die die Quelle bei ausgeschalteter Rückkopplung sieht, Rin = R1 = R11 // RB // rπ1, und bei eingeschalteter Rückkopplung (aber ohne Vorsteuerung)
R i n = R 1 1 + β F B A O L , {\displaystyle R_{\mathrm {in} }={\frac {R_{1}}{1+{\beta }_{\mathrm {FB} }A_{\mathrm {OL} }}} ,}

wobei die Teilung verwendet wird, weil der Eingangsanschluss ein Nebenschluss ist: der Rückkopplungszweipol ist parallel zur Signalquelle auf der Eingangsseite des Verstärkers. Zur Erinnerung: AOL ist die oben ermittelte Verstärkung der offenen Schleife unter Last, die durch die Widerstände des Rückkopplungsnetzwerks modifiziert wird.
Die Impedanz, die von der Last gesehen wird, muss weiter diskutiert werden. Die Last in Abbildung 5 ist mit dem Kollektor des Ausgangstransistors verbunden und daher durch die unendliche Impedanz der Ausgangsstromquelle vom Körper des Verstärkers getrennt. Daher hat die Rückkopplung keine Auswirkung auf die Ausgangsimpedanz, die einfach RC2 bleibt, wie der Lastwiderstand RL in Abbildung 3 zeigt.
Wenn wir stattdessen die Impedanz am Emitter des Ausgangstransistors (statt an seinem Kollektor) finden wollten, der mit dem Rückkopplungsnetzwerk in Reihe geschaltet ist, würde die Rückkopplung diesen Widerstand um den Verbesserungsfaktor ( 1 + βFB AOL) erhöhen.
Lastspannung und LaststromEdit
Die oben abgeleitete Verstärkung ist die Stromverstärkung am Kollektor des Ausgangstransistors. Um diesen Verstärkungsfaktor mit dem Verstärkungsfaktor am Ausgang des Verstärkers in Beziehung zu setzen, ist zu beachten, dass die Ausgangsspannung an der Last RL mit dem Kollektorstrom durch das ohmsche Gesetz als vL = iC (RC2 || RL) verbunden ist. Folglich erhält man die Transistorverstärkung vL / iS durch Multiplikation der Stromverstärkung mit RC2 || RL:
v L i S = A F B ( R C 2 ∥ R L ) . {\displaystyle {\frac {v_{\mathrm {L} }}{i_{\mathrm {S} }}=A_{\mathrm {FB} }(R_{\mathrm {C2} }\parallel R_{\mathrm {L} })\ .}

Wenn der Ausgang des Verstärkers als der Strom im Lastwiderstand RL betrachtet wird, bestimmt die Stromteilung den Laststrom, und die Verstärkung ist dann:
i L i S = A F B R C 2 R C 2 + R L. {\displaystyle {\frac {i_{\mathrm {L} }}{i_{\mathrm {S} }}}=A_{\mathrm {FB} }{\frac {R_{\mathrm {C2} }}{R_{\mathrm {C2} }+R_{\mathrm {L} }}}\ .}

Ist der Hauptverstärkerblock ein Zweitor?Edit

Es folgen für den aufmerksamen Leser einige Nachteile des Zwei-Tor-Ansatzes.
Abbildung 7 zeigt das Kleinsignalschaltbild mit dem Hauptverstärker und dem Rückkopplungs-Zwei-Tor in schattierten Kästen. Das rückgekoppelte Zweitor erfüllt die Torbedingungen: am Eingangstor tritt Iin ein und verlässt das Tor, und am Ausgang tritt Iout ein und verlässt das Tor.
Ist der Hauptverstärkerblock auch ein Zweitor? Der Hauptverstärker ist im oberen schattierten Kasten dargestellt. Die Masseanschlüsse sind beschriftet. Abbildung 7 zeigt die interessante Tatsache, dass der Hauptverstärker die Anschlussbedingungen an seinem Eingang und Ausgang nicht erfüllt, es sei denn, die Masseanschlüsse werden so gewählt, dass dies möglich ist. Auf der Eingangsseite ist der Strom, der in den Hauptverstärker fließt, beispielsweise IS. Dieser Strom wird auf drei Arten aufgeteilt: auf das Rückkopplungsnetzwerk, auf den Vorspannungswiderstand RB und auf den Basiswiderstand des Eingangstransistors rπ. Um die Anschlussbedingung für den Hauptverstärker zu erfüllen, müssen alle drei Komponenten zur Eingangsseite des Hauptverstärkers zurückgeführt werden, d. h. alle mit G1 bezeichneten Masseleitungen sowie die Emitterleitung GE1 müssen angeschlossen werden. Ebenso müssen auf der Ausgangsseite alle mit G2 bezeichneten Masseanschlüsse und auch der Masseanschluss GE2 angeschlossen werden. Unten im Schaltplan, unterhalb des Rückkopplungs-Doppelanschlusses und außerhalb der Verstärkerblöcke, ist G1 mit G2 verbunden. Dadurch werden die Erdströme wie geplant zwischen der Eingangs- und der Ausgangsseite aufgeteilt. Beachten Sie, dass diese Anschlussanordnung den Emitter des Eingangstransistors in eine Basis- und eine Kollektorseite aufteilt – eine physikalisch unmögliche Sache, aber elektrisch betrachtet die Schaltung alle Masseverbindungen als einen Knoten, so dass diese Fiktion zulässig ist.
Natürlich macht die Art und Weise, wie die Masseverbindungen angeschlossen sind, keinen Unterschied für den Verstärker (sie sind alle ein Knoten), aber sie macht einen Unterschied für die Anschlussbedingungen. Diese Künstlichkeit ist eine Schwäche dieses Ansatzes: Die Anschlussbedingungen werden benötigt, um die Methode zu rechtfertigen, aber die Schaltung wird in Wirklichkeit nicht davon beeinflusst, wie die Ströme zwischen den Masseanschlüssen ausgetauscht werden.
Wenn jedoch keine mögliche Anordnung der Massebedingungen zu den Anschlussbedingungen führt, verhält sich die Schaltung möglicherweise nicht auf die gleiche Weise. Die Verbesserungsfaktoren (1 + βFB AOL) zur Bestimmung der Eingangs- und Ausgangsimpedanz funktionieren dann möglicherweise nicht. Diese Situation ist unangenehm, da das Versäumnis, eine Schaltung mit zwei Anschlüssen zu erstellen, ein echtes Problem (es ist einfach nicht möglich) oder einen Mangel an Vorstellungskraft widerspiegeln kann (z. B. wurde einfach nicht daran gedacht, den Emitterknoten in zwei Teile zu teilen). Daher gibt es bei Zweifeln an den Anschlussbedingungen mindestens zwei Möglichkeiten, um festzustellen, ob die Verbesserungsfaktoren zutreffend sind: Entweder man simuliert ein Beispiel mit Spice und vergleicht die Ergebnisse mit der Verwendung eines Verbesserungsfaktors, oder man berechnet die Impedanz mit einer Testquelle und vergleicht die Ergebnisse.
Eine praktischere Möglichkeit besteht darin, den Ansatz mit zwei Anschlüssen ganz fallen zu lassen und verschiedene Alternativen zu verwenden, die auf der Signalflussgraphen-Theorie basieren, darunter die Rosenstark-Methode, die Choma-Methode und die Verwendung des Blackman-Theorems. Diese Wahl kann ratsam sein, wenn Kleinsignal-Bauelementemodelle komplex sind oder nicht zur Verfügung stehen (z. B. wenn die Bauelemente nur numerisch bekannt sind, vielleicht aus Messungen oder SPICE-Simulationen).