Ein elektromagnetisches Metamaterial beeinflusst elektromagnetische Wellen, die auf seine strukturellen Merkmale, die kleiner als die Wellenlänge sind, auftreffen oder mit ihnen wechselwirken. Um sich wie ein homogenes Material zu verhalten, das durch einen effektiven Brechungsindex genau beschrieben wird, müssen seine Merkmale viel kleiner als die Wellenlänge sein.

Für Mikrowellenstrahlung liegen die Merkmale in der Größenordnung von Millimetern. Metamaterialien für den Mikrowellenbereich werden in der Regel als Anordnungen elektrisch leitender Elemente (z. B. Drahtschleifen) mit geeigneten induktiven und kapazitiven Eigenschaften hergestellt. Viele Mikrowellen-Metamaterialien verwenden geteilte Ringresonatoren.

Photonische Metamaterialien sind im Nanometerbereich strukturiert und manipulieren Licht bei optischen Frequenzen. Photonische Kristalle und frequenzselektive Oberflächen wie Beugungsgitter, dielektrische Spiegel und optische Beschichtungen weisen Ähnlichkeiten mit strukturierten Metamaterialien im Subwellenlängenbereich auf. Diese werden jedoch in der Regel von Metamaterialien unterschieden, da ihre Funktion durch Beugung oder Interferenz entsteht und sie daher nicht als homogenes Material betrachtet werden können. Materialstrukturen wie photonische Kristalle sind jedoch im sichtbaren Lichtspektrum wirksam. Die Mitte des sichtbaren Spektrums hat eine Wellenlänge von etwa 560 nm (für Sonnenlicht). Photonische Kristallstrukturen sind in der Regel halb so groß oder kleiner, d. h. <280 nm.

Plasmonische Metamaterialien nutzen Oberflächenplasmonen, d. h. Pakete elektrischer Ladung, die an den Oberflächen von Metallen bei optischen Frequenzen gemeinsam oszillieren.

Frequenzselektive Oberflächen (FSS) können Eigenschaften im Subwellenlängenbereich aufweisen und werden auch als künstliche magnetische Leiter (AMC) oder Hochimpedanzoberflächen (HIS) bezeichnet. FSS weisen induktive und kapazitive Eigenschaften auf, die direkt mit ihrer Subwellenlängenstruktur zusammenhängen.

Elektromagnetische Metamaterialien können wie folgt in verschiedene Klassen eingeteilt werden:

Negativer BrechungsindexBearbeiten

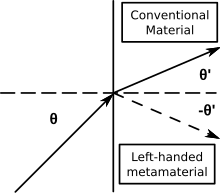
Negativ-Index-Metamaterialien (NIM) sind durch einen negativen Brechungsindex gekennzeichnet. Andere Bezeichnungen für NIMs sind „linkshändige Medien“, „Medien mit negativem Brechungsindex“ und „Rückwärtswellen-Medien“. NIMs, bei denen der negative Brechungsindex aus einer gleichzeitig negativen Permittivität und negativen Permeabilität resultiert, werden auch als doppelt negative Metamaterialien oder doppelt negative Materialien (DNG) bezeichnet.

Ausgehend von einem Material, das durch eine reelle Permittivität und Permeabilität gut approximiert wird, ist die Beziehung zwischen Permittivität ϵ r {\displaystyle \epsilon _{r}}

, Permeabilität μ r {\displaystyle \mu _{r}}

und der Brechungsindex n ist gegeben durch n = ± ϵ r μ r {\displaystyle \scriptstyle n=\pm {\sqrt {\epsilon _{\mathrm {r} }\mu _{\mathrm {r} }}}}

. Alle bekannten nicht-metamateriellen transparenten Materialien (Glas, Wasser, …) besitzen ein positives ϵ r {\displaystyle \epsilon _{r}}

und μ r {\displaystyle \mu _{r}}

. Konventionell wird für n die positive Quadratwurzel verwendet. Einige technische Metamaterialien haben jedoch ϵ r {\displaystyle \epsilon _{r}}

und μ r < 0 {\displaystyle \mu _{r}<0}

. Da das Produkt ϵ r μ r {\displaystyle \epsilon _{r}\mu _{r}}

positiv ist, ist n real. Unter solchen Umständen ist es notwendig, die negative Quadratwurzel für n zu nehmen. Wenn sowohl ϵ r {\displaystyle \epsilon _{r}}

und μ r {\displaystyle \mu _{r}}

positiv (negativ) sind, breiten sich Wellen in Vorwärts- (Rückwärts-) Richtung aus. Elektromagnetische Wellen können sich in Materialien mit ϵ r {\displaystyle \epsilon _{r}}

und μ r {\displaystyle \mu _{r}}

mit entgegengesetztem Vorzeichen, wenn der Brechungsindex imaginär wird. Solche Materialien sind undurchlässig für elektromagnetische Strahlung und Beispiele sind plasmonische Materialien wie Metalle (Gold, Silber, …).

Die vorstehenden Überlegungen sind für reale Materialien vereinfacht, die komplexwertige ϵ r {\displaystyle \epsilon _{r}}

und μ r {\displaystyle \mu _{r}}

. Die Realteile von sowohl ϵ r {\displaystyle \epsilon _{r}}

und μ r {\displaystyle \mu _{r}}

müssen nicht negativ sein, damit ein passives Material eine negative Brechung aufweist. In der Tat kann ein negativer Brechungsindex für zirkular polarisierte Wellen auch durch Chiralität entstehen. Metamaterialien mit negativem n haben zahlreiche interessante Eigenschaften:

• Das Snellsche Gesetz (n1sinθ1 = n2sinθ2) beschreibt zwar immer noch die Brechung, aber da n2 negativ ist, befinden sich einfallende und gebrochene Strahlen an einer Grenzfläche von Materialien mit positivem und negativem Index auf derselben Seite der Oberflächennormale.
• Die Cherenkov-Strahlung zeigt in die andere Richtung.
• Der zeitgemittelte Poynting-Vektor ist antiparallel zur Phasengeschwindigkeit. Damit sich aber Wellen (Energie) ausbreiten können, muss ein -µ mit einem -ε gepaart sein, um die Wellenzahlabhängigkeit von den Materialparametern k c = ω μ ϵ {\displaystyle kc=\omega {\sqrt {\mu \epsilon }} zu erfüllen.}
  

  .

Der negative Brechungsindex leitet sich mathematisch aus dem Vektortripel E, H und k ab.

Für ebene Wellen, die sich in elektromagnetischen Metamaterialien ausbreiten, folgen das elektrische Feld, das magnetische Feld und der Wellenvektor einer Linkshänderregel, also dem umgekehrten Verhalten herkömmlicher optischer Materialien.

Bislang weisen nur Metamaterialien einen negativen Brechungsindex auf.

Einfach negativBearbeiten

Einfach negative (SNG) Metamaterialien haben entweder eine negative relative Permittivität (εr) oder eine negative relative Permeabilität (µr), aber nicht beides. Sie wirken als Metamaterialien, wenn sie mit einem anderen, komplementären SNG kombiniert werden und gemeinsam als DNG wirken.

Epsilon-negative Medien (ENG) zeigen ein negatives εr, während µr positiv ist. Viele Plasmen weisen diese Eigenschaft auf. Zum Beispiel sind Edelmetalle wie Gold oder Silber im infraroten und sichtbaren Spektrum ENG.

Mu-negative Medien (MNG) weisen ein positives εr und ein negatives µr auf. Gyrotropische oder gyromagnetische Materialien weisen diese Eigenschaft auf. Ein gyrotropes Material ist ein Material, das durch das Vorhandensein eines quasistatischen Magnetfeldes verändert wurde, was einen magneto-optischen Effekt ermöglicht. Ein magneto-optischer Effekt ist ein Phänomen, bei dem sich eine elektromagnetische Welle durch ein solches Medium ausbreitet. In einem solchen Material können sich links- und rechtsdrehende elliptische Polarisationen mit unterschiedlichen Geschwindigkeiten ausbreiten. Wenn Licht durch eine Schicht aus magneto-optischem Material übertragen wird, nennt man das Ergebnis den Faraday-Effekt: Die Polarisationsebene kann gedreht werden, wodurch ein Faraday-Rotator entsteht. Die Ergebnisse einer solchen Reflexion werden als magneto-optischer Kerr-Effekt bezeichnet (nicht zu verwechseln mit dem nichtlinearen Kerr-Effekt). Zwei gyrotrope Materialien mit umgekehrten Drehrichtungen der beiden Hauptpolarisationen werden als optische Isomere bezeichnet.

Das Zusammenfügen einer Platte aus ENG-Material und einer Platte aus MNG-Material führt zu Eigenschaften wie Resonanzen, anomalem Tunneln, Transparenz und Nullreflexion. Wie Materialien mit negativem Index sind SNGs von Natur aus dispersiv, so dass ihre εr, µr und ihr Brechungsindex n eine Funktion der Frequenz sind.

HyperbolicEdit

Hyperbolische Metamaterialien (HMMs) verhalten sich für eine bestimmte Polarisation oder Richtung der Lichtausbreitung wie ein Metall und für die andere wie ein Dielektrikum, was auf die negativen und positiven Komponenten des Permittivitätstensors zurückzuführen ist und eine extreme Anisotropie ergibt. Die Dispersionsrelation des Materials im Wellenvektorraum bildet ein Hyperboloid, weshalb es als hyperbolisches Metamaterial bezeichnet wird. Die extreme Anisotropie von HMMs führt zu einer gerichteten Ausbreitung von Licht innerhalb und auf der Oberfläche. HMMs haben verschiedene potentielle Anwendungen gezeigt, wie z.B. Sensorik, Bildgebung, Lenkung von optischen Signalen, verstärkte Plasmonenresonanzeffekte.

BandgapEdit

Elektromagnetische Bandlücken-Metamaterialien (EBG oder EBM) steuern die Lichtausbreitung. Dies wird entweder mit photonischen Kristallen (PC) oder linkshändigen Materialien (LHM) erreicht. PCs können die Ausbreitung von Licht gänzlich unterbinden. Beide Klassen können die Ausbreitung von Licht in bestimmten, festgelegten Richtungen ermöglichen, und beide können mit Bandlücken bei gewünschten Frequenzen entworfen werden. Die Periodengröße von EBGs ist ein beträchtlicher Bruchteil der Wellenlänge, was zu konstruktiver und destruktiver Interferenz führt.

PCs unterscheiden sich von Strukturen unterhalb der Wellenlänge, wie z. B. abstimmbare Metamaterialien, da PCs ihre Eigenschaften aus ihren Bandlückencharakteristiken ableiten. PCs sind so groß, dass sie der Wellenlänge des Lichts entsprechen, im Gegensatz zu anderen Metamaterialien, die eine Struktur mit geringer Wellenlänge aufweisen. Außerdem funktionieren PCs durch Beugung von Licht. Im Gegensatz dazu nutzen Metamaterialien keine Beugung.

PCs haben periodische Einschlüsse, die die Wellenausbreitung aufgrund der destruktiven Interferenz der Einschlüsse durch Streuung hemmen. Die Eigenschaft der photonischen Bandlücke von PCs macht sie zum elektromagnetischen Analogon elektronischer Halbleiterkristalle.

EBGs haben das Ziel, hochwertige, verlustarme, periodische, dielektrische Strukturen zu schaffen. Ein EBG wirkt auf Photonen in der gleichen Weise wie Halbleitermaterialien auf Elektronen. PCs sind das perfekte Bandlückenmaterial, da sie keine Lichtausbreitung zulassen. Jede Einheit der vorgeschriebenen periodischen Struktur verhält sich wie ein Atom, wenn auch von viel größerer Größe.

EBGs sind so konzipiert, dass sie die Ausbreitung einer bestimmten Bandbreite von Frequenzen für bestimmte Einfallswinkel und Polarisationen verhindern. Es wurden verschiedene Geometrien und Strukturen vorgeschlagen, um die besonderen Eigenschaften von EBGs zu erzeugen. In der Praxis ist es unmöglich, ein makelloses EBG-Bauteil zu bauen.

EBGs wurden für Frequenzen von einigen Gigahertz (GHz) bis zu einigen Terahertz (THz), Radio, Mikrowellen und mittlere Infrarotfrequenzen hergestellt. Zu den EBG-Anwendungsentwicklungen gehören eine Übertragungsleitung, Holzpfähle aus quadratischen dielektrischen Stäben und verschiedene Arten von Antennen mit geringem Gewinn.

Doppelt positives MediumEdit

Doppelpositive Medien (DPS) kommen in der Natur vor, wie z. B. natürlich vorkommende Dielektrika. Die Permittivität und die magnetische Permeabilität sind beide positiv und die Wellenausbreitung erfolgt in Vorwärtsrichtung. Es wurden künstliche Materialien hergestellt, die DPS-, ENG- und MNG-Eigenschaften in sich vereinen.

Bi-isotrop und bianisotropEdit

Bei der Kategorisierung von Metamaterialien in doppelt oder einfach negativ bzw. doppelt positiv wird normalerweise davon ausgegangen, dass das Metamaterial unabhängige elektrische und magnetische Antworten hat, die durch ε und µ beschrieben werden. In vielen Fällen verursacht jedoch das elektrische Feld eine magnetische Polarisierung, während das magnetische Feld eine elektrische Polarisierung hervorruft, was als magnetoelektrische Kopplung bekannt ist. Solche Medien werden als bi-isotrop bezeichnet. Medien, die magnetoelektrische Kopplung aufweisen und anisotrop sind (was bei vielen Metamaterialstrukturen der Fall ist), werden als bi-anisotrop bezeichnet.

Vier Materialparameter sind für die magnetoelektrische Kopplung von bi-isotropen Medien von entscheidender Bedeutung. Es sind die elektrische (E) und magnetische (H) Feldstärke sowie die elektrische (D) und magnetische (B) Flussdichte. Diese Parameter sind ε, µ, κ und χ bzw. Dielektrizitätskonstante, Permeabilität, Chiralitätsstärke und der Tellegen-Parameter. Bei dieser Art von Medien ändern sich die Materialparameter nicht bei Änderungen entlang eines gedrehten Koordinatensystems der Messungen. In diesem Sinne sind sie invariant oder skalar.

Die intrinsischen magnetoelektrischen Parameter, κ und χ, beeinflussen die Phase der Welle. Die Wirkung des Chiralitätsparameters besteht in der Aufspaltung des Brechungsindexes. In isotropen Medien führt dies nur dann zu einer Wellenausbreitung, wenn ε und µ das gleiche Vorzeichen haben. In bi-isotropen Medien, bei denen χ als Null angenommen wird und κ einen Wert ungleich Null hat, ergeben sich andere Ergebnisse. Es kann entweder eine Rückwärtswelle oder eine Vorwärtswelle auftreten. Alternativ können zwei Vorwärtswellen oder zwei Rückwärtswellen auftreten, abhängig von der Stärke des Chiralitätsparameters.

Im allgemeinen Fall lauten die konstitutiven Beziehungen für bi-anisotrope Materialien D = ϵ E + ξ H , {\displaystyle \mathbf {D} =\epsilon \mathbf {E} +\xi \mathbf {H} ,}

B = ζ E + μ H , {\displaystyle \mathbf {B} =\zeta \mathbf {E} +\mu \mathbf {H} ,}

wobei ϵ {\displaystyle \epsilon }

und μ {\displaystyle \mu }

sind die Permittivität bzw. der Permeabilitätstensor, während ξ {\displaystyle \xi }

und ζ {\displaystyle \zeta }

sind die beiden magneto-elektrischen Tensoren. Wenn das Medium reziprok ist, sind Permittivität und Permeabilität symmetrische Tensoren, und ξ = – ζ T = – i κ T {\displaystyle \xi =-\zeta ^{T}=-i\kappa ^{T}}

, wobei κ {\displaystyle \kappa }

der chirale Tensor ist, der das chirale elektromagnetische und reziproke magneto-elektrische Verhalten beschreibt. Der chirale Tensor kann ausgedrückt werden als κ = 1 3 tr ( κ ) I + N + J {\displaystyle \kappa ={\tfrac {1}{3}}\operatorname {tr} (\kappa )I+N+J}

, wobei tr ( κ ) {\displaystyle \operatorname {tr} (\kappa )}

ist die Spur von κ {\displaystyle \kappa }

, I ist die Identitätsmatrix, N ist ein symmetrischer spurenfreier Tensor und J ist ein antisymmetrischer Tensor. Eine solche Zerlegung ermöglicht es uns, die reziproke bianisotrope Reaktion zu klassifizieren, und wir können die folgenden drei Hauptklassen identifizieren: (i) chirale Medien ( tr ( κ ) ≠ 0 , N ≠ 0 , J = 0 {\displaystyle \operatorname {tr} (\kappa )\neq 0,N\neq 0,J=0}

), (ii) pseudochirale Medien ( tr ( κ ) = 0 , N ≠ 0 , J = 0 {\displaystyle \operatorname {tr} (\kappa )=0,N\neq 0,J=0}

), (iii) omega media ( tr ( κ ) = 0 , N = 0 , J ≠ 0 {\displaystyle \operatorname {tr} (\kappa )=0,N=0,J\neq 0}

).

ChiralEdit

Die Händigkeit von Metamaterialien ist eine potenzielle Quelle der Verwirrung, da in der Metamaterialliteratur zwei widersprüchliche Verwendungen der Begriffe links- und rechtshändig vorkommen. Der erste bezieht sich auf eine der beiden zirkular polarisierten Wellen, die die Ausbreitungsmoden in chiralen Medien sind. Der zweite bezieht sich auf das Triplett aus elektrischem Feld, magnetischem Feld und Poynting-Vektor, das in Medien mit negativem Brechungsindex auftritt, die in den meisten Fällen nicht chiral sind.

Im Allgemeinen ist eine chirale und/oder bianisotrope elektromagnetische Antwort eine Folge der geometrischen 3D-Chiralität: 3D-chirale Metamaterialien werden durch Einbettung 3D-chiraler Strukturen in ein Wirtsmedium gebildet und zeigen chiralitätsbezogene Polarisationseffekte wie optische Aktivität und zirkulären Dichroismus. Das Konzept der 2D-Chiralität existiert ebenfalls, und ein planares Objekt wird als chiral bezeichnet, wenn es nicht mit seinem Spiegelbild überlagert werden kann, es sei denn, es wird aus der Ebene herausgehoben. Bei 2D-chiralen Metamaterialien, die anisotrop und verlustbehaftet sind, wurde beobachtet, dass sie aufgrund der zirkularen Konversionsdichrosie eine richtungsasymmetrische Übertragung (Reflexion, Absorption) von zirkular polarisierten Wellen aufweisen. Andererseits kann eine bianisotrope Reaktion aus geometrisch achiralen Strukturen entstehen, die weder 2D- noch 3D-intrinsische Chiralität besitzen. Plum und Kollegen untersuchten die magneto-elektrische Kopplung aufgrund extrinsischer Chiralität, bei der sich die Anordnung einer (achiralen) Struktur zusammen mit dem Strahlungswellenvektor von ihrem Spiegelbild unterscheidet, und beobachteten eine große, abstimmbare lineare optische Aktivität, nichtlineare optische Aktivität, spiegelnde optische Aktivität und zirkulären Konversionsdichroismus. Rizza et al. schlugen 1D-chirale Metamaterialien vor, bei denen der effektive chirale Tensor nicht verschwindet, wenn das System geometrisch eindimensional chiral ist (das Spiegelbild der gesamten Struktur kann nicht durch Translationen ohne Rotationen überlagert werden).

3D-chirale Metamaterialien sind aus chiralen Materialien oder Resonatoren aufgebaut, bei denen der effektive Chiralitätsparameter κ {\displaystyle \kappa }

ungleich Null ist. Wellenausbreitungseigenschaften in solchen chiralen Metamaterialien zeigen, dass negative Brechung in Metamaterialien mit einer starken Chiralität und positivem ϵ r {\displaystyle \epsilon _{r}}

und μ r {\displaystyle \mu _{r}}

. Dies liegt daran, dass der Brechungsindex n {\displaystyle n}

für links und rechts zirkular polarisierte Wellen unterschiedliche Werte hat, gegeben durch

n = ± ϵ r μ r ± κ {\displaystyle n=\pm {\sqrt {\epsilon _{r}\mu _{r}}} \kappa }

Es ist zu erkennen, dass ein negativer Index für eine Polarisation auftritt, wenn κ {\displaystyle \kappa }

> ϵ r μ r {\displaystyle {\sqrt {\epsilon _{r}\mu _{r}}}}

. In diesem Fall ist es nicht notwendig, dass einer oder beide ϵ r {\displaystyle \epsilon _{r}}

und μ r {\displaystyle \mu _{r}}

für die rückwärtige Wellenausbreitung negativ sein. Ein negativer Brechungsindex aufgrund von Chiralität wurde erstmals gleichzeitig und unabhängig voneinander von Plum et al. und Zhang et al. im Jahr 2009 beobachtet.

FSS basedEdit

Frequenzselektive oberflächenbasierte Metamaterialien blockieren Signale in einem Wellenbereich und lassen sie in einem anderen Wellenbereich durch. Sie haben sich zu einer Alternative zu Metamaterialien mit fester Frequenz entwickelt. Sie ermöglichen optionale Änderungen der Frequenzen in einem einzigen Medium, statt der restriktiven Einschränkungen eines festen Frequenzgangs.