Im Tutorial über verallgemeinerte lineare Modelle haben wir verschiedene GLMs wie lineare Regression, logistische Regression, etc. kennengelernt. In diesem Tutorial der R-Tutorial-Serie von TechVidvan werden wir uns die lineare Regression in R im Detail ansehen. Wir werden lernen, was die lineare Regression in R ist und wie man sie in R implementiert. Wir werden uns die Methode der kleinsten Quadrate ansehen und lernen, wie man die Genauigkeit des Modells überprüft.

So, ohne weitere Umschweife, lasst uns loslegen!

Lineare Regression in R

Lineare Regression in R ist eine Methode zur Vorhersage des Wertes einer Variablen unter Verwendung des Wertes/der Werte einer oder mehrerer Eingabe-Prädiktorvariablen. Das Ziel der linearen Regression ist es, eine lineare Beziehung zwischen der gewünschten Ausgangsvariablen und den Eingangsvorhersagevariablen herzustellen.

Eine kontinuierliche Variable Y als Funktion einer oder mehrerer Eingangsvorhersagevariablen Xi zu modellieren, so dass die Funktion zur Vorhersage des Wertes von Y verwendet werden kann, wenn nur die Werte von Xi bekannt sind. Die allgemeine Form einer solchen linearen Beziehung ist:

Y=?0+?1 X

Hier ist ?0 der Achsenabschnitt
und ?1 die Steigung.

Typen der linearen Regression in R

Es gibt zwei Arten der linearen Regression in R:

• Einfache lineare Regression
• Mehrfache lineare Regression

Schauen wir uns diese einzeln an.

Einfache lineare Regression in R

Die einfache lineare Regression zielt darauf ab, eine lineare Beziehung zwischen zwei kontinuierlichen Variablen zu finden. Dabei ist zu beachten, dass es sich um eine statistische und nicht um eine deterministische Beziehung handelt.

Eine deterministische Beziehung ist eine Beziehung, bei der der Wert einer Variablen durch den Wert der anderen Variablen genau bestimmt werden kann. Ein Beispiel für eine deterministische Beziehung ist die Beziehung zwischen Kilometern und Meilen. Anhand des Kilometerwerts können wir die Entfernung in Meilen genau bestimmen. Eine statistische Beziehung ist nicht genau und hat immer einen Vorhersagefehler. Wenn wir beispielsweise genügend Daten haben, können wir eine Beziehung zwischen der Größe und dem Gewicht einer Person finden, aber es wird immer eine Fehlerspanne geben, und es wird Ausnahmefälle geben.

Die Idee hinter der einfachen linearen Regression ist es, eine Linie zu finden, die am besten zu den gegebenen Werten der beiden Variablen passt. Diese Linie kann uns dann helfen, die Werte der abhängigen Variable zu finden, wenn sie fehlen.

Lassen Sie uns dies anhand eines Beispiels untersuchen. Wir haben einen Datensatz, der aus den Größen und Gewichten von 500 Personen besteht. Unser Ziel ist es, ein lineares Regressionsmodell zu erstellen, das die Beziehung zwischen Größe und Gewicht so formuliert, dass wir bei der Eingabe der Größe (Y) in das Modell das Gewicht (X) mit einer minimalen Fehlermarge erhalten.

Y=b0+b1X

Die Werte von b0 und b1 sollten so gewählt werden, dass sie die Fehlermarge minimieren. Die Fehlermetrik kann verwendet werden, um die Genauigkeit des Modells zu messen.

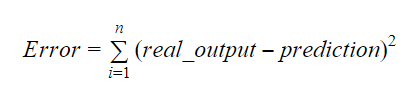
Wir können die Steigung oder den Koeffizienten wie folgt berechnen: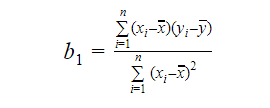

Der Wert von b1 gibt uns einen Einblick in die Art der Beziehung zwischen den abhängigen und den unabhängigen Variablen.

• Wenn b1 > 0 ist, dann haben die Variablen eine positive Beziehung, d.h. Wenn b1 < 0, dann haben die Variablen eine negative Beziehung, d.h. eine Zunahme von x führt zu einer Abnahme von y.
• Wenn b1 < 0, dann haben die Variablen eine negative Beziehung, d.h. eine Zunahme von x führt zu einer Abnahme von y.

Der Wert von b0 oder der Achsenabschnitt kann wie folgt berechnet werden: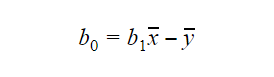
Der Wert von b0 kann ebenfalls viele Informationen über das Modell liefern und umgekehrt.

Wenn das Modell x=0 nicht enthält, dann ist die Vorhersage ohne b1 bedeutungslos. Damit das Modell an einem beliebigen Punkt nur b0 und nicht b1 enthält, muss der Wert von x an diesem Punkt 0 sein. In Fällen wie der Körpergröße kann x nicht 0 sein, und die Körpergröße einer Person kann nicht 0 sein. Daher ist ein solches Modell mit nur b0 bedeutungslos.

Wenn der Term b0 fehlt, geht das Modell durch den Ursprung, was bedeutet, dass die Vorhersage und der Regressionskoeffizient (Steigung) verzerrt sind.

Multiple lineare Regression in R

Multiple lineare Regression ist eine Erweiterung der einfachen linearen Regression. Bei der multiplen linearen Regression wird versucht, ein lineares Modell zu erstellen, das den Wert der Zielvariablen anhand der Werte mehrerer Vorhersagevariablen vorhersagen kann. Die allgemeine Form einer solchen Funktion ist wie folgt:

Y=b0+b1X1+b2X2+…+bnXn

Bewertung der Genauigkeit des Modells

Es gibt verschiedene Methoden zur Bewertung der Qualität und Genauigkeit des Modells. Schauen wir uns einige dieser Methoden nacheinander an.

R-Quadrat

Die eigentliche Information in den Daten ist die darin enthaltene Varianz. Das R-Quadrat gibt an, welcher Anteil der Variation der Zielvariablen (y) durch das Modell erklärt wird. Das R-Quadrat eines Modells lässt sich mit der folgenden Formel ermitteln: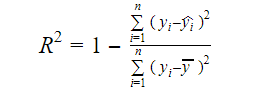

Wobei,

• yi der angepasste Wert von y für die Beobachtung i
• y der Mittelwert von Y ist.

Ein niedriger Wert von R-Quadrat bedeutet eine geringere Genauigkeit des Modells. Das R-Quadrat-Maß ist jedoch nicht notwendigerweise ein entscheidender Faktor.

Bereinigtes R-Quadrat

Wenn die Anzahl der Variablen im Modell steigt, steigt auch der R-Quadrat-Wert. Dies führt auch zu Fehlern in der Variation, die durch die neu hinzugefügten Variablen erklärt wird. Daher passen wir die Formel für R-Quadrat für mehrere Variablen an.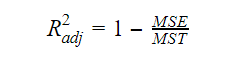
Hier steht der MSE für den mittleren Standardfehler, der ist:

und MST steht für die mittlere Standardsumme, die gegeben ist durch: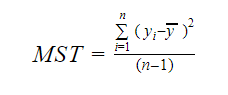

Wobei n die Anzahl der Beobachtungen und q die Anzahl der Koeffizienten ist.

Die Beziehung zwischen R-Quadrat und bereinigtem R-Quadrat ist: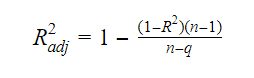

Standardfehler und F-Statistik

Der Standardfehler und die F-Statistik sind beides Maße für die Qualität der Anpassung eines Modells. Die Formeln für Standardfehler und F-Statistik lauten:

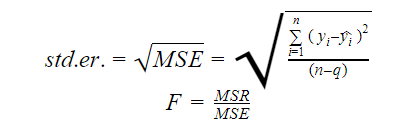
wobei MSR für Mean Square Regression steht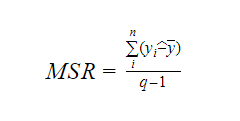

AIC und BIC

Akaike’s Information Criterion und Bayesian Information Criterion sind Maße für die Qualität der Anpassung von statistischen Modellen. Sie können auch als Kriterien für die Auswahl eines Modells verwendet werden.

AIC=(-2)*ln(L)+2*k
BIC=(-2)*ln(L)+k*ln(n)

Wobei,

• L die Likelihood-Funktion ist,
• k die Anzahl der Modellparameter ist,
• n die Stichprobengröße ist.

lm-Funktion in R

Die lm()-Funktion von R passt lineare Modelle an. Sie kann Regression, Varianz- und Kovarianzanalyse durchführen. Die Syntax der Funktion lm lautet wie folgt:

lm(formula, data, subset, weights, na.action,method = "qr", model = TRUE, x = FALSE, y = FALSE, qr = TRUE,singular.ok = TRUE, offset, …)

Wobei,

• formula ein Objekt der Klasse „formula“ und eine symbolische Darstellung des anzupassenden Modells ist,
• data der Datenrahmen oder die Liste ist, die die Variablen in der Formel enthält(data ist ein optionales Argument. Wenn es fehlt, holt die Funktion die Variablen aus der Umgebung),
• subset ist ein optionaler Vektor, der eine Untermenge von Beobachtungen enthält, die im Anpassungsprozess verwendet werden sollen,
• weights ist ein optionaler Vektor, der die Gewichte angibt, die im Anpassungsprozess verwendet werden sollen,
• na.action ist eine Funktion, die angibt, was geschehen soll, wenn NAs in den Daten vorkommen,
• method bezeichnet die Methode zur Anpassung des Modells,
• model, x, y und qr sind logische Werte, die steuern, ob entsprechende Werte mit der Ausgabe zurückgegeben werden sollen oder nicht. Diese Werte sind:
• model: der Modellrahmen
• x: die Modellmatrix
• y: die Antwort
• qr: die qr-Zerlegung
• singular.ok ist ein Logical, das steuert, ob singuläre Anpassungen erlaubt sind oder nicht,
• offset ist ein im Voraus bekannter Prädiktor, der im Modell verwendet werden soll,
• . . . sind zusätzliche Argumente, die an die Regressionsfunktionen auf niedrigerer Ebene übergeben werden.

Praktisches Beispiel für lineare Regression in R

Das ist genug Theorie für den Moment. Schauen wir uns nun an, wie man das alles implementiert. Wir werden ein lineares Modell mithilfe der linearen Regression in R mit Hilfe der Funktion lm() anpassen. Anschließend werden wir auch die Anpassungsqualität des Modells überprüfen. Wir verwenden den Autos-Datensatz, der standardmäßig im R-Basispaket enthalten ist.

1. Wir beginnen mit einer grafischen Analyse des Datensatzes, um uns mit ihm vertraut zu machen. Dazu zeichnen wir ein Streudiagramm und prüfen, was es uns über die Daten sagt.

Wir können die Funktion scatter.smooth() verwenden, um ein Streudiagramm für den Datensatz zu erstellen.

scatter.smooth(x=cars$speed,y=cars$dist,main="TechVidvan Dist ~ Speed")

Output

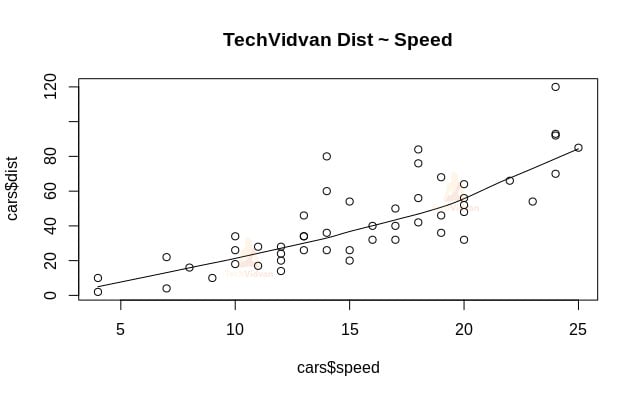
Das Streudiagramm zeigt uns eine positive Korrelation zwischen Entfernung und Geschwindigkeit. Sie deutet auf eine linear ansteigende Beziehung zwischen den beiden Variablen hin. Damit eignen sich die Daten für die lineare Regression, da eine lineare Beziehung eine Grundannahme für die Anpassung eines linearen Modells an die Daten ist.

2. Nachdem wir nun überprüft haben, dass die lineare Regression für die Daten geeignet ist, können wir die Funktion lm() verwenden, um ein lineares Modell an die Daten anzupassen.

Linear_model <- lm(dist~speed,data=cars)print(Linear_model)

Ausgabe

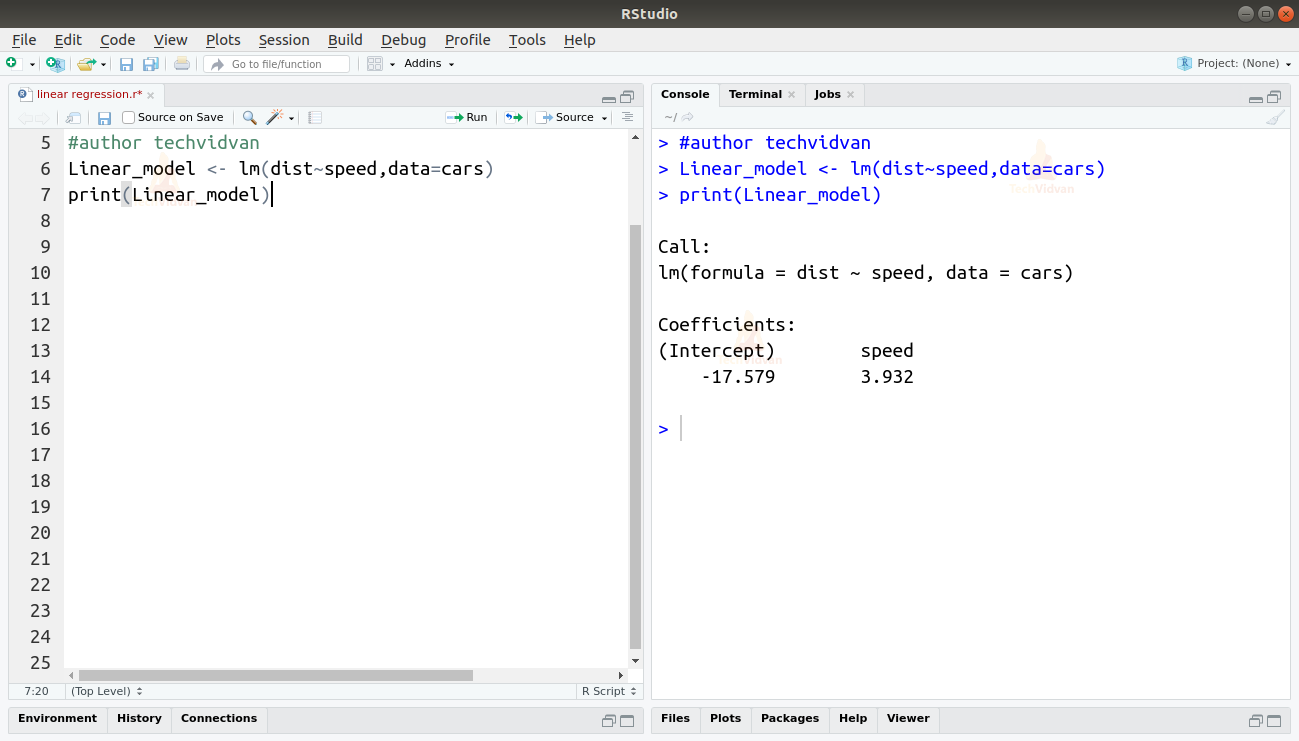
Die Ausgabe der lm()-Funktion zeigt uns den Achsenabschnitt und den Koeffizienten der Geschwindigkeit. Damit wird die lineare Beziehung zwischen Entfernung und Geschwindigkeit wie folgt definiert:

Entfernung=Achsenabschnitt+Koeffizient*Geschwindigkeit

Entfernung=-17,579+3,932*Geschwindigkeit

3. Nachdem wir nun ein Modell angepasst haben, wollen wir die Qualität oder Güte der Anpassung überprüfen. Beginnen wir mit der Überprüfung der Zusammenfassung des linearen Modells, indem wir die Funktion summary() verwenden.

summary(Linear_model)

Output

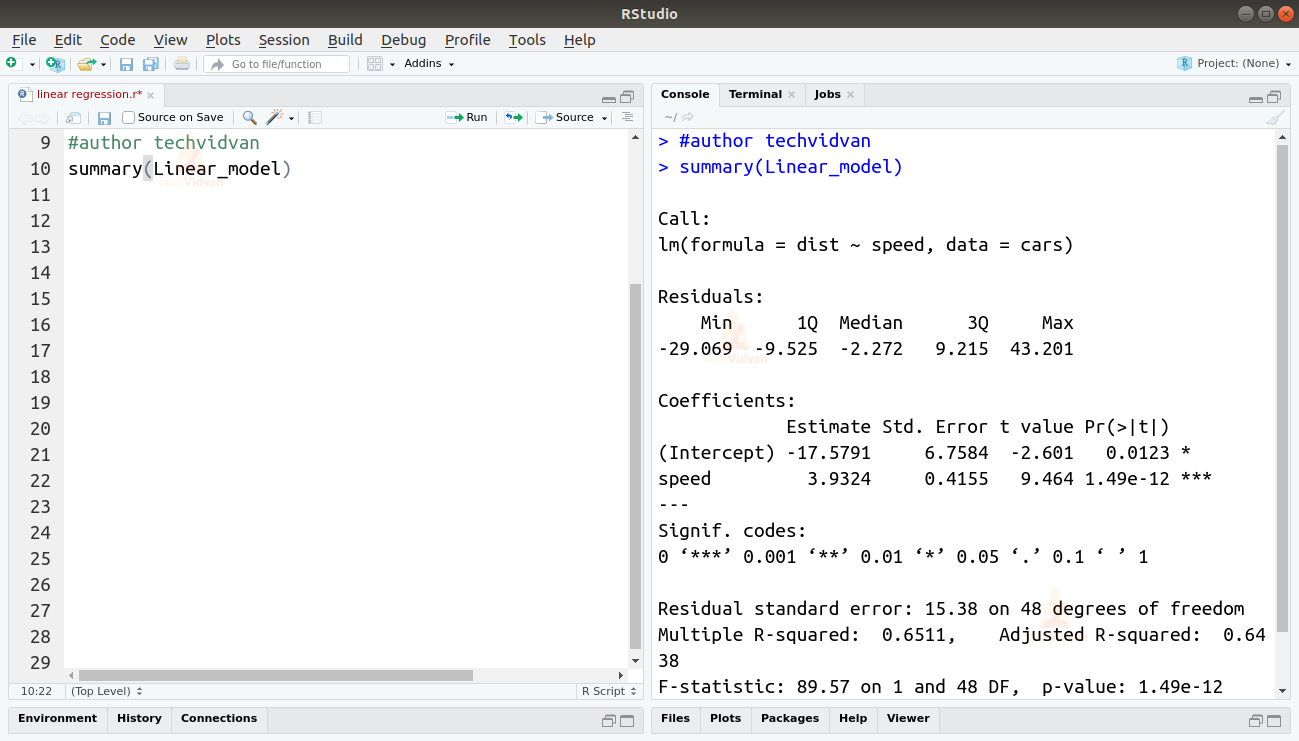
Die Funktion summary() gibt uns einige wichtige Maße an die Hand, um die Anpassung des Modells zu diagnostizieren. Der p-Wert ist ein wichtiges Maß für die Güte der Anpassung eines Modells. Ein Modell gilt als nicht geeignet, wenn der p-Wert über einem vorher festgelegten statistischen Signifikanzniveau liegt, das im Idealfall 0,05 beträgt.

Die Zusammenfassung liefert auch den t-Wert. Je höher der t-Wert ist, desto besser ist das Modell geeignet.
Wir können auch den AIC und BIC mit den Funktionen AIC() und BIC() ermitteln.

AIC(Linear_model)BIC(Linear_model)

Output

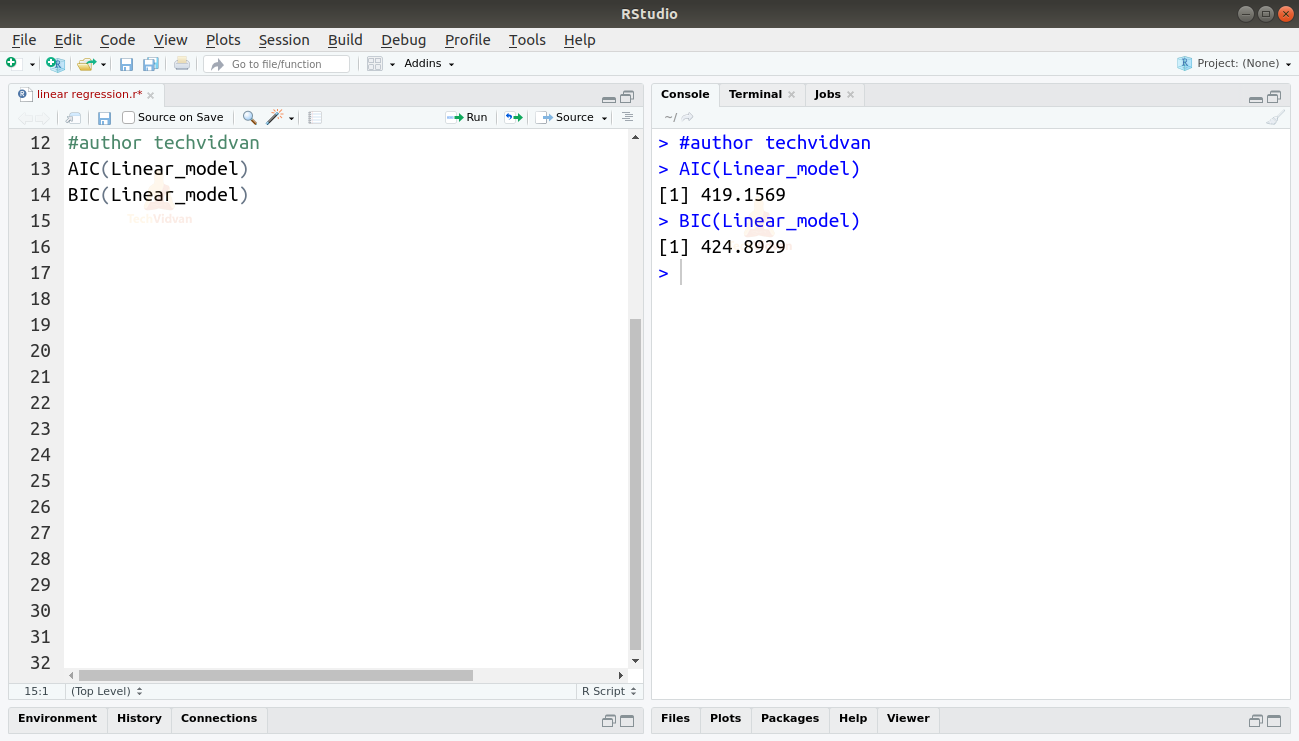
Das Modell, das die niedrigsten AIC- und BIC-Werte ergibt, wird am meisten bevorzugt.

Zusammenfassung

In diesem Kapitel der R-Tutorial-Reihe von TechVidvan haben wir etwas über lineare Regression gelernt. Wir lernten die einfache lineare Regression und die multiple lineare Regression kennen. Dann haben wir verschiedene Maße zur Bewertung der Qualität oder Genauigkeit des Modells untersucht, wie R2, bereinigtes R2, Standardfehler, F-Statistik, AIC und BIC. Dann lernten wir, wie man die lineare Regression in R implementiert. Anschließend überprüften wir die Qualität der Anpassung des Modells in R.

Teilen Sie Ihre Bewertung auf Google, wenn Ihnen das Tutorial über lineare Regression gefallen hat.