Hallo Leute! In diesem Artikel werde ich einen Algorithmus beschreiben, der in der natürlichen Sprachverarbeitung verwendet wird: Latent Semantic Analysis ( LSA ).
Die Hauptanwendungsgebiete dieser oben genannten Methode sind in der Linguistik sehr vielfältig: Vergleich von Dokumenten in niedrigdimensionalen Räumen (Document Similarity), Auffinden wiederkehrender Themen in Dokumenten (Topic Modeling), Auffinden von Beziehungen zwischen Begriffen (Text Synoymity).

Einführung

Das Modell der latenten semantischen Analyse ist eine Theorie dafür, wie Bedeutungsrepräsentationen
aus der Begegnung mit großen Sprachmustern ohne explizite Hinweise darauf, wie diese strukturiert sind, gelernt werden können.
Das vorliegende Problem ist nicht überwacht, d.h. wir haben keine festen Etiketten oder Kategorien, die dem Korpus zugewiesen sind.

Um Muster aus den Dokumenten zu extrahieren und zu verstehen, folgt die LSA naturgemäß bestimmten Annahmen:
1) Die Bedeutung von Sätzen oder Dokumenten ist eine Summe der Bedeutung aller darin vorkommenden Wörter. Insgesamt ist die Bedeutung eines bestimmten Wortes ein Durchschnitt über alle Dokumente, in denen es vorkommt.
2) LSA geht davon aus, dass die semantischen Assoziationen zwischen Wörtern nicht explizit, sondern nur latent in der großen Stichprobe der Sprache vorhanden sind.

Mathematische Perspektive

Latent Semantic Analysis (LSA) umfasst bestimmte mathematische Operationen, um Einblicke in ein Dokument zu erhalten. Dieser Algorithmus bildet die Grundlage des Topic Modeling. Der Kerngedanke besteht darin, eine Matrix aus den vorhandenen Dokumenten und Begriffen in eine separate Dokument-Thema-Matrix und eine Thema-Begriff-Matrix zu zerlegen.

Der erste Schritt besteht darin, unsere Dokument-Begriff-Matrix mit Hilfe des Tf-IDF-Vektorisierers zu erstellen. Sie kann auch mit Hilfe eines Bag-of-Words-Modells konstruiert werden, aber die Ergebnisse sind spärlich und liefern keine Aussagekraft.
Gegeben m Dokumente und n-Wörter in unserem Vokabular, können wir eine
m × n Matrix A konstruieren, in der jede Zeile ein Dokument und jede Spalte ein Wort darstellt.

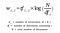
Intuitiv hat ein Term ein großes Gewicht, wenn er häufig im Dokument, aber selten im Korpus vorkommt.
Mit Hilfe dieser Transformationsmethode (tf-IDF) bilden wir eine Dokument-Term-Matrix, A, um unseren Korpus zu vektorisieren. (In einer Weise, die unser weiteres Modell verarbeiten bzw. auswerten kann, da wir noch nicht mit Strings arbeiten!)
Aber es gibt einen subtilen Nachteil, wir können aus der Beobachtung von A nichts ableiten, da es sich um eine verrauschte und spärliche Matrix handelt. (

Da Topic Modeling von Natur aus ein unüberwachter Algorithmus ist, müssen wir die latenten Themen im Voraus festlegen. Es ist analog zum K-Means Clustering, so dass wir die Anzahl der Cluster vorher festlegen.

In diesem Fall führen wir eine Low-Rank-Annäherung mit einer Dimensionalitätsreduktionstechnik durch, die eine abgeschnittene Singulärwertzerlegung (SVD) verwendet.
Die Singulärwertzerlegung ist eine Technik in der linearen Algebra, die eine beliebige Matrix M in das Produkt von 3 separaten Matrizen faktorisiert: M=U*S*V, wobei S eine Diagonalmatrix der Singulärwerte von M ist.

Die verkürzte SVD reduziert die Dimensionalität, indem sie nur die t größten Singulärwerte auswählt und nur die ersten t Spalten von U und V behält. In diesem Fall ist t ein Hyperparameter, den wir auswählen und anpassen können, um die Anzahl der Themen, die wir finden wollen, zu reflektieren.

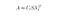
Anmerkung: Truncated SVD macht die Dimensionalitätsreduktion und nicht die SVD!

Mit diesen Dokumentvektoren und Termvektoren können wir nun leicht Maße wie die Kosinusähnlichkeit anwenden, um sie zu bewerten:

• die Ähnlichkeit verschiedener Dokumente
• die Ähnlichkeit verschiedener Wörter
• die Ähnlichkeit von Begriffen (oder „Abfragen“) und Dokumenten (was beim Information Retrieval nützlich ist, wenn wir die für unsere Suchanfrage relevantesten Passagen abrufen wollen).

Abschließende Bemerkungen

Dieser Algorithmus wird hauptsächlich bei verschiedenen NLP-basierten Aufgaben verwendet und ist die Grundlage für robustere Methoden wie Probabilistic LSA und Latent Dirichlet Allocation (LDA).

Kushal Vala, Junior Data Scientist bei Datametica Solutions Pvt Ltd