
In diesem Artikel werde ich die Grundlagen der Qualitätserhaltung vorstellen.
Dazu gehören Qualitätssicherung, Qualitätskontrolle und Metrologie. Die Qualitätssicherung dient dazu, das Vertrauen zu gewinnen, dass die Qualitätsanforderungen erfüllt werden. Die Qualitätskontrolle dient dazu, zu überprüfen, ob die Anforderungen erfüllt wurden. Dies ist ein feiner Unterschied, und in der Praxis werden die Begriffe manchmal synonym verwendet. Metrologie ist die Wissenschaft vom Messen. Sie stellt sicher, dass wir die Ergebnisse von Messungen, die überall auf der Welt durchgeführt werden, zuverlässig vergleichen können.
Diese Grundsätze können für Produkte oder Dienstleistungen gelten, aber ich werde mich auf die Fertigung konzentrieren und darauf, wie diese drei grundlegenden Konzepte in diesem Zusammenhang zusammenhängen. Ich habe daher die Details spezifischer Methoden vermieden und gehe nicht auf die Mathematik ein. Das werde ich mir für einen späteren Artikel aufheben.
Die Ursprünge des Messens
Die Ägypter verwendeten Maßstäbe mit regelmäßigen Kalibrierungen, um sicherzustellen, dass die Steine in ihren großen Bauprojekten zusammenpassen. Die modernen Qualitätssysteme entstanden jedoch erst während der industriellen Revolution. Davor wurden mechanische Produkte von Handwerkern hergestellt, die jedes Teil einzeln anpassten, damit es in eine Baugruppe passte. Das bedeutete, dass jede Maschine und jedes Teil in ihr einzigartig war. Wenn ein Teil ersetzt werden musste, musste ein Handwerker ein neues Teil einbauen.
Im späten 18. Jahrhundert begannen die französischen Waffenhersteller, Musketen mit Standardteilen herzustellen. Das bedeutete, dass die Armee Ersatzteile mit sich führen und diese schnell gegen kaputte Teile austauschen konnte. Diese austauschbaren Teile wurden immer noch geputzt, um in die Baugruppe zu passen, aber anstatt jedes Teil an die einzelne Waffe anzupassen, wurde es an ein Hauptteil angepasst.
Einige Jahre später begannen amerikanische Waffenhersteller, diese Methode zu verwenden, passten sie aber an ihre ungeschulten Arbeiter an. Sie feilten Lehren zur Anpassung an das Meisterteil, die Arbeiter stellten mit Hilfe der Lehren Vorrichtungen und Produktionsmaschinen ein und benutzten die Lehren auch zur Überprüfung der Teile. Auf diese Weise konnte eine Reihe von Maschinen, die jeweils einen einzigen Arbeitsgang mit einem ungelernten Bediener durchführten, präzise Teile herstellen. Die Teile konnten dann schnell zu komplexen Maschinen zusammengesetzt werden.
Der Grundstein für die moderne Fertigung war damit gelegt, mehr als 100 Jahre bevor Ford diese Ideen auf ein sich bewegendes Fließband anwenden würde.
Kalibrierung, wahrer Wert und Messfehler
Ein System von Meisterteilen, Lehren und Einwegmaschinen funktionierte, als ein ganzes Produkt in einer einzigen Fabrik hergestellt wurde. Moderne globale Lieferketten brauchen ein anderes System.
Statt eines physischen Meisterteils haben wir eine Zeichnung oder ein digitales CAD-Modell. Festgelegte Toleranzen stellen sicher, dass die Teile zusammenpassen und wie vorgesehen funktionieren. Anstatt dass jeder Hersteller seine Lehren an einem einzigen Musterteil einstellt, lassen sie ihre Messinstrumente kalibrieren. Die Instrumente werden dann zur Einstellung der Produktionsmaschinen und zur Kontrolle der hergestellten Teile verwendet.
Die gesamte Qualität hängt von diesem Kalibrierungsprozess ab.
Das wichtigste Konzept, das man verstehen muss, ist, dass alle Messungen mit Unsicherheiten behaftet sind. Wenn ich Sie bitten würde, die Höhe dieses Textes zu schätzen, würden Sie vielleicht sagen: „Es sind ungefähr 4 mm“. Die Verwendung des Wortes „ungefähr“ impliziert, dass Ihre Schätzung mit einer gewissen Unsicherheit behaftet ist.
In der Tat können wir nie den genauen wahren Wert von irgendetwas wissen, alle Messungen sind eigentlich Schätzungen und haben eine gewisse Unsicherheit. Die Differenz zwischen einem Messergebnis und dem wahren Wert ist der Messfehler. Da wir den wahren Wert nicht kennen können, können wir auch den Fehler nicht kennen: es handelt sich um unbestimmbare Größen.
Alles, was wir über die Welt um uns herum quantifizieren können, sind die Ergebnisse von Messungen, und diese sind immer mit einer gewissen Unsicherheit behaftet, auch wenn diese Unsicherheit sehr klein ist.
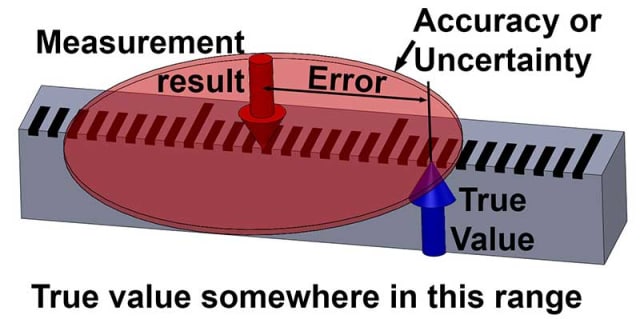
Wenn Sie die Höhe dieses Textes auf „etwa 4 mm, plus/minus 1 mm“ schätzen würden, dann haben Sie jetzt Ihrer Unsicherheit einige Grenzen zugewiesen. Aber du kannst dir immer noch nicht zu 100 Prozent sicher sein, dass es stimmt.
Sie haben vielleicht ein gewisses Maß an Vertrauen, sagen wir 95 Prozent, dass es wahr ist. Wenn Sie die Grenzen erhöhen, sagen wir um 2 mm, dann würde Ihr Vertrauen steigen, vielleicht auf 99 Prozent. Die Unsicherheit gibt also einige Grenzen vor, innerhalb derer wir ein gewisses Maß an Vertrauen haben, dass der wahre Wert liegt.
OK, die Philosophiestunde ist vorbei!
In einem zukünftigen Beitrag werde ich auf diese Ideen eingehen und erläutern, wie die Unsicherheit für ein bestimmtes Vertrauensniveau berechnet werden kann.
Unsicherheit und Qualität
Sobald wir die Unsicherheit (oder „Genauigkeit“) einer Messung bestimmt haben, können wir dies anwenden, um zu entscheiden, ob ein Teil mit einer bestimmten Toleranz übereinstimmt. Nehmen wir zum Beispiel an, dass ein Teil 100 mm +/- 1 mm betragen soll. Wir messen es und erhalten ein Ergebnis von 100,87 mm.
Liegt das Teil innerhalb der Spezifikation?
Die einfache Antwort lautet: „Wir wissen es nicht, vielleicht ist es so, aber vielleicht gab es einen Fehler bei unserer Messung und das Teil ist tatsächlich größer als 101 mm. Vielleicht gab es einen noch größeren Fehler und das Teil ist tatsächlich weniger als 99 mm!“
Solange wir nicht wissen, wie groß die Messunsicherheit ist, haben wir keine Ahnung, wie sicher wir sein können, dass das Teil innerhalb der Spezifikationen liegt. Nehmen wir an, dass die Messunsicherheit so angegeben wurde, dass das Messergebnis 100,87 mm +/- 0,1 mm bei einer Zuverlässigkeit von 95 % beträgt. Jetzt können wir mit mehr als 95 Prozent Sicherheit sagen, dass das Teil innerhalb der Spezifikation liegt.
Das Verständnis und die Quantifizierung der Messunsicherheit ist also entscheidend für die Aufrechterhaltung der Qualität.
Betrachten wir nun die Kalibrierung und das damit verbundene Konzept der Rückverfolgbarkeit. Dies ist ein grundlegender Aspekt der Unsicherheit. Eine Kalibrierung ist ein Vergleich mit einer Referenz, und die Unsicherheit dieses Vergleichs muss aus den unten erläuterten Gründen immer mit einbezogen werden.
Eine rückführbare Messung ist eine Messung, die eine ununterbrochene Kette von Kalibrierungen aufweist, die bis zum Primärnormal zurückreicht. Im Fall von Längenmessungen ist das Primärnormal die Definition des Meters, d.h. die Strecke, die das Licht im Vakuum in 1/299.792.458 Sekunden zurücklegt, wie sie vom Internationalen Büro für Maß und Gewicht (BIPM) in Paris festgelegt wurde.
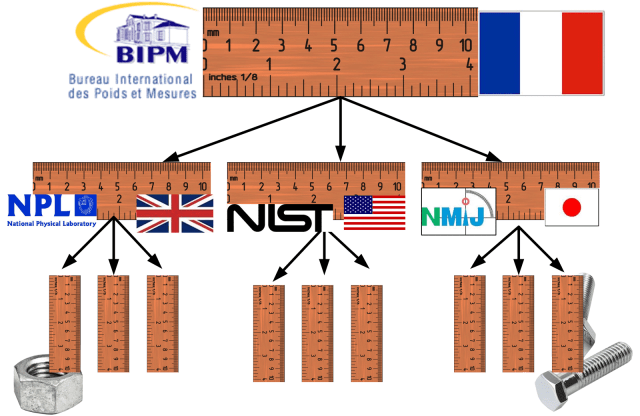
Seit den 1930er Jahren ist das Zollmaß als 25,4 mm definiert und daher auch auf das gleiche Meter-Normal rückführbar. Alle Maße müssen auf dieselbe Norm zurückgeführt werden können, damit die in verschiedenen Ländern hergestellten Teile zusammenpassen.
Unsicherheit und Fehler
Die Unsicherheit von Messungen entsteht aus verschiedenen Quellen. Einige davon führen zu einem beständigen Fehler oder einer Verzerrung des Ergebnisses.
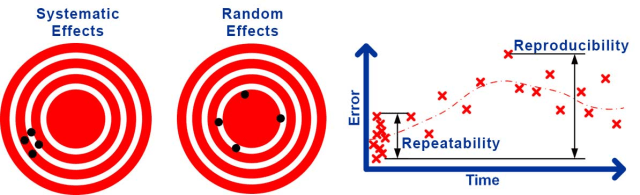
Zum Beispiel führt der unbekannte Fehler, der bei der Kalibrierung eines Instruments auftritt, zu einem konstanten Fehler, wann immer es verwendet wird. Diese Art von Effekt wird als systematische Unsicherheit bezeichnet, die zu einem systematischen Fehler führt. Andere Quellen führen zu Fehlern, die sich jedes Mal, wenn eine Messung durchgeführt wird, zufällig ändern.
Zum Beispiel können Turbulenzen in der Luft kleine, sich zufällig ändernde Störungen bei Lasermessungen verursachen, mechanisches Spiel und Ausrichtung können zufällig wechselnde Fehler bei mechanischen Messungen verursachen. Diese Art von Effekt ist als zufällige Unsicherheit bekannt, die zu einem zufälligen Fehler führt.
Es ist üblich, die zufällige Unsicherheit in Wiederholbarkeit , die zufällige Unsicherheit der Ergebnisse unter gleichen Bedingungen, und Reproduzierbarkeit , die zufällige Unsicherheit unter veränderten Bedingungen, zu unterteilen.
Natürlich können die Bedingungen nie genau gleich oder völlig unterschiedlich sein, so dass die Unterscheidung etwas ungenau ist. Die Arten von Bedingungen, die geändert werden können, sind die Durchführung der Messung zu einer anderen Zeit, mit einem anderen Bediener, einem anderen Instrument, unter Verwendung einer anderen Kalibrierung und in einer anderen Umgebung.
Es gibt zwei weit verbreitete Methoden zur Quantifizierung der Unsicherheit einer Messung. Kalibrierlaboratorien und wissenschaftliche Einrichtungen führen in der Regel eine Unsicherheitsbewertung nach dem Leitfaden zur Angabe der Messunsicherheit (GUM) durch.
Bei der GUM-Methode werden zunächst alle Einflüsse berücksichtigt, die das Messergebnis beeinflussen könnten. Anschließend muss ein mathematisches Modell ermittelt werden, das das Messergebnis in Abhängigkeit von diesen Einflussgrößen angibt. Durch Berücksichtigung der Unsicherheit in jeder Eingangsgröße und Anwendung des ‚ Gesetzes der Unsicherheitsfortpflanzung ‚ kann ein Schätzwert für die kombinierte Unsicherheit der Messung berechnet werden.
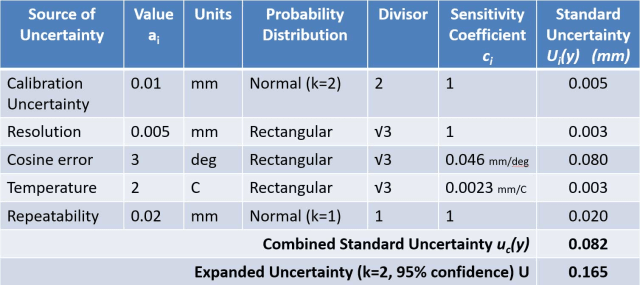
Der GUM-Ansatz wird manchmal als „bottom-up“ bezeichnet, da er mit der Betrachtung jedes einzelnen Einflusses beginnt. Jeder Einfluss wird normalerweise in einer Tabelle aufgeführt, die als Unsicherheitsbudget bezeichnet wird und zur Berechnung der kombinierten Unsicherheit verwendet wird.
Industrielle Messprozesse werden in der Regel mit Hilfe einer Messsystemanalyse (MSA) bewertet, wie sie im Rahmen der Six-Sigma-Methodik empfohlen wird und in der Regel den Richtlinien des MSA-Referenzhandbuchs der Automotive Industry Action Group (AIAG) folgt.
MSA beinhaltet die Durchführung von Prüfmittelstudien, bei denen wiederholte Messungen mit einer Referenz unter verschiedenen Bedingungen verglichen werden, um die Verzerrung, Wiederholbarkeit und manchmal Reproduzierbarkeit zu bestimmen.
Eine Typ-1-Messgerätestudie ist eine Schnellprüfung, die normalerweise durchgeführt wird, um die Abweichungen eines Messgeräts zu verstehen. Dabei misst ein einzelner Bediener ein einzelnes kalibriertes Referenzteil 25 oder mehr Mal und betrachtet dann die Schwankungen und Verzerrungen der Ergebnisse. Diese Art von Test wird außerhalb von MSA oft als Wiederholbarkeitsstudie bezeichnet.
Eine Studie zur Wiederholbarkeit und Reproduzierbarkeit von Prüfmitteln (Gage R&R) wird verwendet, um ein detaillierteres Verständnis eines Messprozesses zu erhalten. In der Regel werden 10 Teile jeweils zweimal von mindestens drei verschiedenen Bedienern gemessen. Mit Hilfe eines statistischen Verfahrens namens ANOVA wird dann ermittelt, wie viel Abweichung durch das Messgerät („Gage“) und wie viel durch den Bediener verursacht wird. Dabei werden der Wechsel des Bedieners und nachfolgende Änderungen in Zeit und Umgebung als vollständige Darstellung der Reproduzierbarkeitsbedingungen betrachtet.
Die MSA wird manchmal auch als Top-Down-Methode bezeichnet, da sie den Messprozess weitgehend als Black-Box behandelt und systematische und zufällige Unsicherheiten experimentell bestimmt. Zwei wichtige Konzepte in der MSA sind die Genauigkeit , die als Äquivalent der Unsicherheit verwendet wird, und die Präzision , die als Äquivalent der zufälligen Unsicherheit verwendet wird.
Der Vorteil der Unsicherheitsbewertung besteht darin, dass sie alle Unsicherheitsquellen berücksichtigen kann und, wenn sie richtig durchgeführt wird, die genaueste Schätzung der Unsicherheit liefert. Zu den Problemen dieses Ansatzes gehört die Tatsache, dass ein Messtechniker erforderlich ist, der in der Lage ist, das mathematische Modell zu erstellen, und dass die Gefahr menschlicher Fehler besteht, die dazu führen, dass wichtige Einflüsse ausgelassen oder falsch geschätzt werden.
Die GUM-Methode ist auch nur für eine einzelne Messung gültig, die mit bekannten Werten für alle angewandten Korrekturen durchgeführt wurde. Es ist daher schwierig, die Unsicherheitsbewertung korrekt anzuwenden, um die Unsicherheit eines industriellen Messprozesses vorherzusagen.
MSA kann viel einfacher angewendet werden und soll eine Vorhersage für die Genauigkeit eines industriellen Messprozesses liefern. Das Problem bei diesem Ansatz ist, dass bestimmte systematische Effekte ignoriert werden und die Reproduzierbarkeitsbedingungen möglicherweise nicht vollständig dargestellt werden, was zu einer Unterschätzung der Unsicherheit führt.
Ein Beispiel für die Nichtberücksichtigung systematischer Effekte ist, dass bei der Bestimmung der Abweichung ein Vergleich mit einer Referenz durchgeführt wird, die als wahrer Wert behandelt wird – in Wirklichkeit hat die Referenz auch eine Unsicherheit, die mit einbezogen werden sollte. Diese Methode beruht darauf, dass alle Reproduzierbarkeitsbedingungen variiert werden, so dass ihre Auswirkungen in der Variation der Ergebnisse bei wiederholten Messungen zu sehen sind. Es ist wahrscheinlich, dass die Art und Weise, in der diese Bedingungen variiert werden, nicht vollständig die Variation widerspiegelt, die während der Dauer des tatsächlichen Messprozesses auftritt.
Messung und Qualitätssicherung
Bisher habe ich mich auf die Qualitätskontrolle konzentriert, d. h. darauf, wie durch Messungen nachgewiesen werden kann, dass die Teile nach ihrer Herstellung den Spezifikationen entsprechen. Betrachten wir nun kurz die Qualitätssicherung, also die Art und Weise, wie wir sicherstellen, dass der Prozess überhaupt gute Teile produziert.
Dieser Aspekt der Qualität wird weitgehend durch die statistische Prozesskontrolle (SPC) abgedeckt. Ein Prozess kann bewertet werden, indem mehrere Teile hergestellt und gemessen werden, um die Schwankungen und Verzerrungen im Herstellungsprozess zu ermitteln. Anstatt diese Ergebnisse direkt anzugeben, ist es üblich, die Teiletoleranz durch die Prozessgenauigkeit zu teilen, um die Werkzeugmaschinenfähigkeit ( C P ) oder durch die Prozessgenauigkeit zu dividieren, um die Prozessfähigkeit ( C PK ) zu erhalten.
SPC ist in vielerlei Hinsicht gleichwertig mit MSA. Sie verfolgt einen Top-Down-Ansatz, um zufällige und systematische Effekte zu verstehen. Anstelle der Auswertung von Messungen wird sie jedoch zur Bewertung des Prozessoutputs verwendet. Sie hat im Allgemeinen die gleichen Vor- und Nachteile wie die MSA, und ein Bottom-up-Ansatz zur Bewertung der Unsicherheit kann verwendet werden, wenn diese ein Problem darstellen.
Auf den ersten Blick mag es so aussehen, als gäbe es grundlegende Unterschiede zwischen MSA und SPC, was auf die sehr unterschiedliche Terminologie innerhalb der SPC zurückzuführen ist. Jedoch ist die Variation mit gemeinsamer Ursache (oder in der älteren Literatur die Variation mit zufälliger Ursache) das Äquivalent der Präzision; die kurzfristige Variabilität ist das Äquivalent der Wiederholbarkeit; die langfristige Variabilität ist das Äquivalent der Reproduzierbarkeit; und die Variation mit besonderer Ursache (oder in der älteren Literatur die Variation mit zuordenbarer Ursache) ist das Äquivalent der Verzerrung.
SPC legt auch einen viel größeren Wert darauf, dass ein Prozess „statistisch kontrolliert“ ist. Im Großen und Ganzen bedeutet dies, dass die Effekte zufällig und normalverteilt sind, wobei alle signifikanten systematischen Effekte korrigiert werden. Dies ist eine Stärke der SPC und wird manchmal sowohl bei der Unsicherheitsbewertung als auch bei der MSA übersehen.
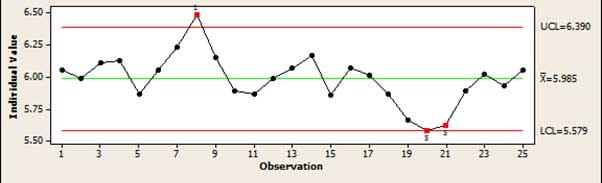
Das Hauptwerkzeug, das in der SPC verwendet wird, um zu prüfen, ob ein Prozess „in Kontrolle“ ist, ist die Regelkarte. Dies ermöglicht eine einfache grafische Darstellung eines Prozesses, bei der leicht zu erkennen ist, ob ein Prozess driftet oder Fehler produziert, die nicht durch normale Zufallsschwankungen erklärt werden können. Wenn z. B. mehrere Punkte ansteigen oder abfallen, deutet dies darauf hin, dass der Prozess driftet.
In diesem Artikel habe ich versucht, einen umfassenden Überblick über ein großes und komplexes Thema zu geben. Ich habe die grundlegenden Prinzipien der Qualitätserhaltung vorgestellt, ohne auf die zur Anwendung dieser Methoden erforderliche Mathematik einzugehen.
Bleiben Sie dran für zukünftige Artikel zu diesen Themen.

Dr. Jody Muelaner begann seine 20-jährige Karriere als Ingenieur in der Maschinenkonstruktion, wo er an allem arbeitete, von medizinischen Geräten bis zu Sägewerken. Seit 2007 entwickelt er an der University of Bath in enger Zusammenarbeit mit führenden Luft- und Raumfahrtunternehmen neuartige Messverfahren. Diese Forschung konzentriert sich derzeit auf die Unsicherheitsmodellierung von Produktionssystemen, wobei Elemente der SPC, MSA und Messtechnik mit neuartigen numerischen Methoden kombiniert werden. Er interessiert sich auch für die Gestaltung von Fahrrädern. Besuchen Sie seine Website für weitere Informationen.