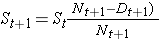Vi er ofte interesseret i at vurdere, om der er forskelle i overlevelse (eller kumulativ forekomst af hændelse) blandt forskellige grupper af deltagere. I et klinisk forsøg med et overlevelsesresultat kan vi f.eks. være interesseret i at sammenligne overlevelsen mellem deltagere, der får et nyt lægemiddel sammenlignet med placebo (eller standardbehandling). I en observationsundersøgelse kan vi være interesseret i at sammenligne overlevelsen mellem mænd og kvinder eller mellem deltagere med og uden en bestemt risikofaktor (f.eks. forhøjet blodtryk eller diabetes). Der findes flere test til at sammenligne overlevelse mellem uafhængige grupper.
Log rank-test
Log rank-testet er en populær test til at teste nulhypotesen om ingen forskel i overlevelse mellem to eller flere uafhængige grupper. Testen sammenligner hele overlevelsesoplevelsen mellem grupperne og kan opfattes som en test af, om overlevelseskurverne er identiske (overlappende) eller ej. Overlevelseskurverne estimeres for hver gruppe, der betragtes separat, ved hjælp af Kaplan-Meier-metoden og sammenlignes statistisk ved hjælp af log-rang-testen. Det er vigtigt at bemærke, at der findes flere varianter af log rang-teststatistikken, som implementeres af forskellige statistiske datapakker (f.eks. SAS, R 4,6). Vi præsenterer her en version, der er tæt knyttet til chi-square-teststatistikken og sammenligner det observerede antal hændelser med det forventede antal hændelser på hvert tidspunkt i opfølgningsperioden.
Eksempel:
Et lille klinisk forsøg gennemføres for at sammenligne to kombinationsbehandlinger hos patienter med fremskreden mavekræft. Tyve deltagere med mavekræft i stadie IV, som giver samtykke til at deltage i forsøget, tildeles tilfældigt til at modtage kemoterapi før operation eller kemoterapi efter operation. Det primære resultat er død, og deltagerne følges i op til 48 måneder (4 år) efter indskrivningen i forsøget. Erfaringerne med deltagerne i hver forsøgsgren er vist nedenfor.
|
Kemoterapi før kirurgi |
|
Kemoterapi efter kirurgi |
||
|---|---|---|---|---|
|
Måned Død |
Måned for sidste kontakt |
|
Måned for død |
Måned for sidste kontakt |
|
8 |
8 |
|
33 |
48 |
|
12 |
32 |
|
28 |
48 |
|
26 |
20 |
|
41 |
25 |
|
14 |
40 |
|
|
37 |
|
21 |
|
|
|
48 |
|
27 |
|
|
|
25 |
|
|
|
|
|
43 |
Seks deltagere i kemoterapi før kirurgi gruppen dør i løbet af opfølg-opfølgning sammenlignet med tre deltagere i kemoterapigruppen efter operation. Andre deltagere i hver gruppe følges i et varierende antal måneder, nogle til undersøgelsens afslutning efter 48 måneder (i kemoterapigruppen efter operation). Ved hjælp af de procedurer, der er skitseret ovenfor, konstruerer vi først livstabeller for hver behandlingsgruppe ved hjælp af Kaplan-Meier-metoden.
Livstabellen for gruppen, der modtager kemoterapi før kirurgi
|
Tid, Måneder |
Antal i risiko Nt |
Antal af dødsfald Dt |
Antal censureret Ct |
Sandsynlighed for overlevelse
|
|---|---|---|---|---|
|
0 |
10 |
|
|
1 |
|
8 |
10 |
1 |
1 |
0.900 |
|
12 |
8 |
1 |
|
0.788 |
|
14 |
7 |
1 |
|
0.675 |
|
20 |
6 |
|
1 |
0.675 |
|
21 |
5 |
1 |
|
0.540 |
|
26 |
4 |
1 |
|
0.405 |
|
27 |
3 |
1 |
|
0.270 |
|
32 |
2 |
|
1 |
0.270 |
|
40 |
1 |
|
1 |
0.270 |
Livstidstabellen for gruppe, der modtager kemoterapi efter operation
|
Tid, Måneder |
Antal i risiko Nt |
Antal af dødsfald Dt |
Antal censureret Ct |
Sandsynlighed for overlevelse
|
|---|---|---|---|---|
|
0 |
10 |
|
|
1 |
|
25 |
10 |
|
2 |
1.000 |
|
28 |
8 |
1 |
|
0.875 |
|
33 |
7 |
1 |
|
0.750 |
|
37 |
6 |
|
1 |
0.750 |
|
41 |
5 |
1 |
|
0.600 |
|
43 |
4 |
|
1 |
0.600 |
|
48 |
3 |
|
3 |
0.600 |
De to overlevelseskurver er vist nedenfor.
Overlevelse i hver behandlingsgruppe
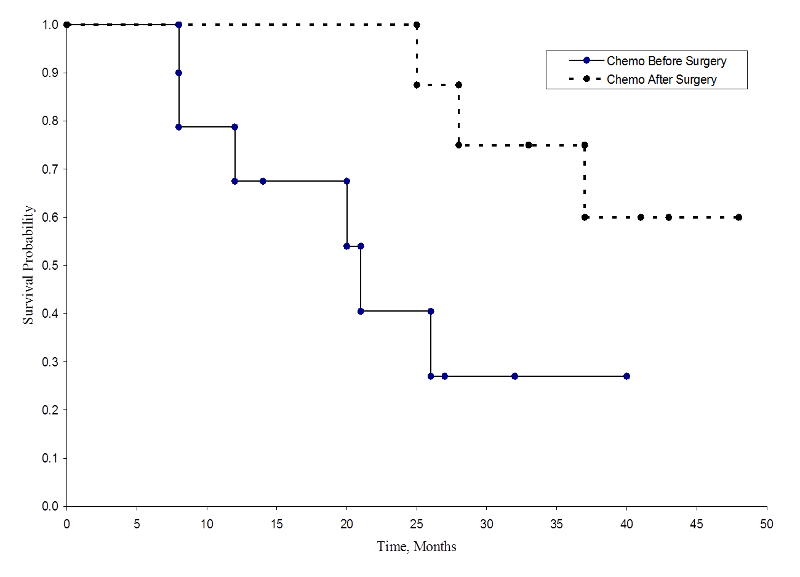
Overlevelsessandsynlighederne for gruppen med kemoterapi efter operation er højere end overlevelsessandsynlighederne for gruppen med kemoterapi før operation, hvilket tyder på en overlevelsesfordel. Disse overlevelseskurver er imidlertid estimeret ud fra små stikprøver. For at sammenligne overlevelsen mellem grupperne kan vi bruge log rank-testen. Nulhypotesen er, at der ikke er nogen forskel i overlevelse mellem de to grupper, eller at der ikke er nogen forskel mellem populationerne i sandsynligheden for død på et hvilket som helst tidspunkt. Log-rang-testen er en ikke-parametrisk test og gør ingen antagelser om overlevelsesfordelingerne. I det væsentlige sammenligner log rang-testen det observerede antal hændelser i hver gruppe med det antal hændelser, der ville være forventet, hvis nulhypotesen var sand (dvs, hvis overlevelseskurverne var identiske).
H0: De to overlevelseskurver er identiske (eller S1t = S2t) versus H1: De to overlevelseskurver er ikke identiske (eller S1t ≠ S2t, på et hvilket som helst tidspunkt t) (α=0,05).
Log rank-statistikken er omtrentligt fordelt som en chi-square-teststatistik. Der findes flere former for teststatistikken, og de varierer med hensyn til, hvordan de beregnes. Vi anvender følgende:
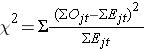
hvor ΣOjt repræsenterer summen af det observerede antal hændelser i den j-te gruppe over tid (f.eks. j=1,2), og ΣEjt repræsenterer summen af det forventede antal hændelser i den j-te gruppe over tid.
Summen af det observerede og det forventede antal hændelser beregnes for hvert hændelsestidspunkt og summeres for hver sammenligningsgruppe. Lograngstatistikken har frihedsgrader lig med k-1, hvor k repræsenterer antallet af sammenligningsgrupper. I dette eksempel er k=2, så teststatistikken har 1 frihedsgrad.
For at beregne teststatistikken har vi brug for det observerede og det forventede antal hændelser på hvert hændelsestidspunkt. Det observerede antal hændelser stammer fra stikprøven, og det forventede antal hændelser beregnes under antagelse af, at nulhypotesen er sand (dvs. at overlevelseskurverne er identiske).
For at generere det forventede antal hændelser organiserer vi dataene i en livstabel med rækker, der repræsenterer hvert hændelsestidspunkt, uanset i hvilken gruppe hændelsen fandt sted. Vi holder også styr på gruppetilknytningen. Vi estimerer derefter andelen af hændelser, der forekommer på hvert tidspunkt (Ot/Nt) ved hjælp af data fra begge grupper kombineret under antagelse af ingen forskel i overlevelse (dvs. under antagelse af, at nulhypotesen er sand). Vi multiplicerer disse estimater med antallet af deltagere i risiko på det pågældende tidspunkt i hver af sammenligningsgrupperne (N1t og N2t for henholdsvis gruppe 1 og 2).
Specifikt beregner vi for hvert hændelsestidspunkt t antallet af deltagere i risiko i hver gruppe, Njt (f.eks. hvor j angiver gruppen, j=1, 2), og antallet af hændelser (dødsfald), Ojt ,i hver gruppe. Nedenstående tabel indeholder de oplysninger, der er nødvendige for at udføre log-rang-testen til sammenligning af ovennævnte overlevelseskurver. Gruppe 1 repræsenterer kemoterapigruppen før operationen, og gruppe 2 repræsenterer kemoterapigruppen efter operationen.
Data til log rang-test for at sammenligne overlevelseskurver
|
Tid, Måneder |
Antal i risiko i gruppe 1
N1t |
Antal i risiko i gruppe 2
N2t |
Antal af hændelser (dødsfald) i gruppe 1
O1t |
Antal af hændelser (dødsfald) i gruppe 2
O2t |
|---|---|---|---|---|
|
8 |
10 |
10 |
1 |
0 |
|
12 |
8 |
10 |
1 |
0 |
|
14 |
7 |
10 |
1 |
0 |
|
21 |
5 |
10 |
1 |
0 |
|
26 |
4 |
8 |
1 |
0 |
|
27 |
3 |
8 |
1 |
0 |
|
28 |
2 |
8 |
0 |
1 |
|
33 |
1 |
7 |
0 |
1 |
|
41 |
0 |
5 |
0 |
1 |
Dernæst summerer vi antallet af risikotransaktioner, Nt = N1t+N2t, på hvert hændelsestidspunkt, og antallet af observerede hændelser (dødsfald), Ot = O1t+O2t, på hvert hændelsestidspunkt. Derefter beregner vi det forventede antal hændelser i hver gruppe. Det forventede antal hændelser beregnes for hvert hændelsestidspunkt på følgende måde:
E1t = N1t*(Ot/Nt) for gruppe 1 og E2t = N2t*(Ot/Nt) for gruppe 2. Beregningerne er vist i nedenstående tabel.
Forventet antal hændelser i hver gruppe
|
Tid, Måneder |
Antal i risiko i gruppe 1 N1t |
Antal i risiko i gruppe 2 N2t |
Totalt antal i risiko Nt |
Antal hændelser i gruppe 1 O1t |
Antal hændelser i gruppe 2 O2t |
Totalt antal hændelser Ot |
Forventet antal hændelser i Gruppe 1 E1t = N1t*(Ot/Nt) |
Forventet antal hændelser i Gruppe 2 E2t = N2t*(Ot/Nt) |
Forventet antal hændelser i Gruppe 2 E2t = N2t*(Ot/Nt) |
|---|---|---|---|---|---|---|---|---|---|
|
8 |
10 |
10 |
20 |
1 |
0 |
1 |
0.500 |
0.500 |
|
|
12 |
8 |
10 |
18 |
1 |
0 |
1 |
0.444 |
0.556 |
|
|
14 |
7 |
10 |
17 |
1 |
0 |
1 |
0.412 |
0.588 |
|
|
21 |
5 |
10 |
15 |
1 |
0 |
1 |
0.333 |
0.667 |
|
|
26 |
4 |
8 |
12 |
1 |
0 |
1 |
0.333 |
0.667 |
|
|
27 |
3 |
8 |
11 |
1 |
0 |
1 |
0.273 |
0.727 |
|
|
28 |
2 |
8 |
10 |
0 |
1 |
1 |
0.200 |
0.800 |
|
|
33 |
1 |
7 |
8 |
0 |
1 |
1 |
0.125 |
0.875 |
|
|
41 |
0 |
5 |
5 |
0 |
1 |
1 |
0.000 |
1.000 |
Dernæst summerer vi det observerede antal hændelser i hver gruppe (∑O1t og ΣO2t) og det forventede antal hændelser i hver gruppe (ΣE1t og ΣE2t) over tid. Disse er vist i den nederste række i den næste tabel nedenfor.
Totalt observeret og forventet antal observerede i hver gruppe
|
Tid, Måneder |
Antal i risiko i gruppe 1 N1t |
Antal i risiko i gruppe 2 N2t |
Totalt antal i risiko Nt |
Antal hændelser i gruppe 1 O1t |
Antal hændelser i gruppe 2 O2t |
Totalt antal hændelser Ot |
Forventet antal hændelser i Gruppe 1 E1t = N1t*(Ot/Nt) |
Forventet antal hændelser i Gruppe 2 E2t = N2t*(Ot/Nt) |
Forventet antal hændelser i Gruppe 2 E2t = N2t*(Ot/Nt) |
|---|---|---|---|---|---|---|---|---|---|
|
8 |
10 |
10 |
20 |
1 |
0 |
1 |
0.500 |
0.500 |
|
|
12 |
8 |
10 |
18 |
1 |
0 |
1 |
0.444 |
0.556 |
|
|
14 |
7 |
10 |
17 |
1 |
0 |
1 |
0.412 |
0.588 |
|
|
21 |
5 |
10 |
15 |
1 |
0 |
1 |
0.333 |
0.667 |
|
|
26 |
4 |
8 |
12 |
1 |
0 |
1 |
0.333 |
0.667 |
|
|
27 |
3 |
8 |
11 |
1 |
0 |
1 |
0.273 |
0.727 |
|
|
28 |
2 |
8 |
10 |
0 |
1 |
1 |
0.200 |
0.800 |
|
|
33 |
1 |
7 |
8 |
0 |
1 |
1 |
0.125 |
0.875 |
|
|
41 |
0 |
5 |
5 |
0 |
1 |
1 |
0.000 |
1.000 |
|
|
|
6 |
3 |
|
2.620 |
6.380 |
Vi kan nu beregne teststatistikken:
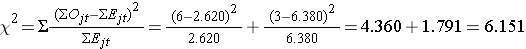
Teststatistikken er omtrentligt fordelt som chi-square med 1 frihedsgrad. Den kritiske værdi for testen kan således findes i tabellen Critical Values of the Χ2 Distribution.
For denne test er beslutningsreglen at forkaste H0, hvis Χ2 > 3,84. Vi observerer Χ2 = 6,151, hvilket overskrider den kritiske værdi på 3,84. Derfor forkaster vi H0. Vi har signifikante beviser, α=0,05, for at vise, at de to overlevelseskurver er forskellige.
Eksempel:
En forsker ønsker at evaluere effektiviteten af en kort intervention for at forebygge alkoholforbrug under graviditet. Gravide kvinder med et tidligere stort alkoholforbrug rekrutteres til undersøgelsen og randomiseres til at modtage enten den korte intervention med fokus på afholdenhed fra alkohol eller standard prænatal pleje. Det interessante resultat er tilbagefald til at drikke igen. Kvinderne rekrutteres til undersøgelsen ved ca. 18 ugers graviditet og følges gennem hele graviditeten indtil fødslen (ca. 39 ugers graviditet). Dataene er vist nedenfor og angiver, om kvinderne begynder at drikke igen, og i bekræftende fald, hvornår de første gang drak, målt i antal uger fra randomiseringen. For kvinder, der ikke får tilbagefald, registrerer vi antallet af uger fra randomiseringen, hvor de er alkoholfri.
|
Standardprænatalbehandling |
|
Kortsigtet intervention |
|||
|---|---|---|---|---|---|
|
Relapse |
Ino Relapse |
|
Relapse |
Ino Relapse |
Ino Relapse |
|
19 |
20 |
|
16 |
21 |
|
|
6 |
19 |
|
21 |
15 |
|
|
5 |
17 |
|
7 |
18 |
|
|
4 |
14 |
|
|
18 |
|
|
|
|
|
|
5 |
|
Det interessante spørgsmål er, om der er en forskel i tid til tilbagefald mellem kvinder, der er tildelt standard prænatal pleje sammenlignet med dem, der er tildelt den korte intervention.
- Strin 1.
Sæt hypoteser op, og bestem signifikansniveauet.
H0: Den tilbagefaldsfrie tid er identisk mellem grupperne versus
H1: Den tilbagefaldsfrie tid er ikke identisk mellem grupperne (α=0,05)
- Strin 2.
Vælg den relevante teststatistik.
Teststatistikken for log rang-testen er
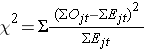
- Stræk 3.
Sæt beslutningsreglen op.
Teststatistikken følger en chi-kvadratfordeling, og vi finder derfor den kritiske værdi i tabellen over kritiske værdier for Χ2-fordelingen) for df=k-1=2-1=1 og α=0,05. Den kritiske værdi er 3,84, og beslutningsreglen er at forkaste H0, hvis Χ2 > 3,84.
- Strin 4.
Beregne teststatistikken.
For at beregne teststatistikken organiserer vi dataene efter hændelsestidspunkter (tilbagefald) og bestemmer antallet af kvinder i risiko i hver behandlingsgruppe og antallet af kvinder, der får tilbagefald på hvert observeret tilbagefaldstidspunkt. I den følgende tabel repræsenterer gruppe 1 kvinder, der modtager standard prænatal pleje, og gruppe 2 repræsenterer kvinder, der modtager den korte intervention.
|
Tidspunkt, Uger |
Antal i risiko – gruppe 1 N1t |
Antal i risiko – gruppe 2 N2t |
Antal tilbagefald – gruppe 1 O1t |
Antal tilbagefald – gruppe 1 O1t |
Antal tilbagefald – gruppe 1 O1t |
Antal tilbagefald – Gruppe 2 O2t |
|---|---|---|---|---|---|---|
|
4 |
8 |
8 |
8 |
1 |
0 |
|
|
5 |
7 |
8 |
1 |
0 |
||
|
6 |
6 |
7 |
1 |
0 |
||
|
7 |
5 |
7 |
0 |
1 |
||
|
16 |
4 |
5 |
0 |
1 |
||
|
19 |
3 |
2 |
1 |
0 |
||
|
21 |
0 |
2 |
0 |
1 |
Dernæst summerer vi antallet af risikogrupper, 
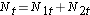, på hvert hændelsestidspunkt, antallet af observerede hændelser (tilbagefald), 
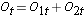, på hvert hændelsestidspunkt og bestemmer det forventede antal tilbagefald i hver gruppe på hvert hændelsestidspunkt ved hjælp af 
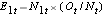og 
.
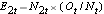Vi summerer derefter det observerede antal hændelser i hver gruppe (ΣO1t og ΣO2t) og det forventede antal hændelser i hver gruppe (ΣE1t og ΣE2t) over tid. Beregningerne for dataene i dette eksempel er vist nedenfor.
| Tid, Uger |
Antal i risikogruppe 1 N1t |
Antal i risikogruppe 2 N2t |
Totalt antal i risikogruppe 1 Nt |
Total antal i risikogruppe 2 Nt |
Antal tilbagefald Gruppe 1 O1t |
Antal tilbagefald Antal tilbagefald Gruppe 2 O2t |
Totalt antal af tilbagefald Ot |
Forventet antal tilbagefald i gruppe 1
|
Forventet antal tilbagefald i gruppe 2
|
|---|---|---|---|---|---|---|---|---|---|
|
4 |
8 |
8 |
16 |
1 |
0 |
1 |
0.500 |
0.500 |
|
|
5 |
7 |
8 |
15 |
1 |
0 |
1 |
0.467 |
0.533 |
|
|
6 |
6 |
7 |
13 |
1 |
0 |
1 |
0.462 |
0.538 |
|
|
7 |
5 |
7 |
12 |
0 |
1 |
1 |
0.417 |
0.583 |
|
|
16 |
4 |
5 |
9 |
0 |
1 |
1 |
0.444 |
0.556 |
|
|
19 |
3 |
2 |
5 |
1 |
0 |
1 |
0.600 |
0.400 |
|
|
21 |
0 |
2 |
2 |
0 |
1 |
1 |
0.000 |
1.000 |
|
|
|
|
|
|
4 |
3 |
|
2.890 |
4.110 |
Vi beregner nu teststatistikken:
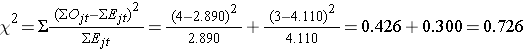
- Stræk 5.
Konklusion. Forkast ikke H0, fordi 0.726 < 3.84. Vi har ikke statistisk signifikant evidens ved α=0,05, der viser, at tiden til tilbagefald er forskellig mellem grupperne.
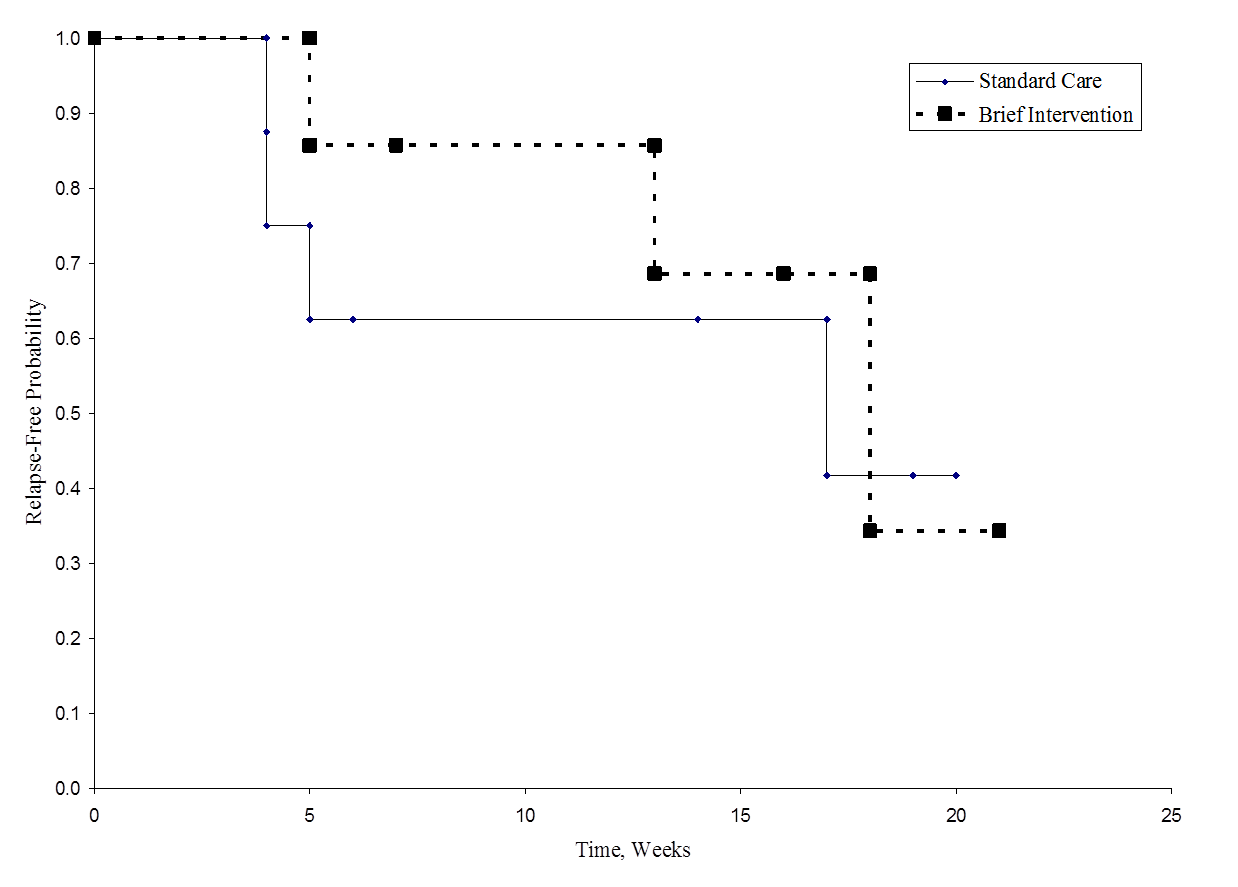
Figuren nedenfor viser overlevelsen (tilbagefaldsfri tid) i hver gruppe. Bemærk, at overlevelseskurverne ikke viser nogen stor adskillelse, hvilket er i overensstemmelse med de ikke-signifikante resultater i hypotesetesten.
Relapse-Free Time in Each Group
Som nævnt er der flere variationer af log rank-statistikken. Nogle statistiske datapakker anvender følgende teststatistik for log rank-testen til sammenligning af to uafhængige grupper:
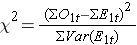
hvor ΣO1t er summen af det observerede antal hændelser i gruppe 1, og ΣE1t er summen af det forventede antal hændelser i gruppe 1 taget over alle hændelsestidspunkter. Nævneren er summen af varianserne af det forventede antal hændelser på hvert hændelsestidspunkt, som beregnes som følger:
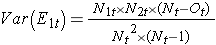
Der findes andre versioner af log rank-statistikken samt andre tests til sammenligning af overlevelsesfunktioner mellem uafhængige grupper.7-9 For eksempel er en populær test den modificerede Wilcoxon-test, som er følsom over for større forskelle i farer tidligere i forhold til senere i opfølgningen.10
retur til toppen | forrige side | næste side