#InsideRL
I et typisk Reinforcement Learning (RL)-problem er der en lærende og en beslutningstager, der kaldes agent, og omgivelserne, som den interagerer med, kaldes miljø. Omgivelserne giver til gengæld belønninger og en ny tilstand baseret på agentens handlinger. Ved forstærkende læring lærer vi altså ikke en agent, hvordan den skal gøre noget, men giver den belønninger, hvad enten de er positive eller negative, på grundlag af dens handlinger. Så vores grundlæggende spørgsmål til denne blog er, hvordan vi matematisk formulerer et problem i RL. Det er her, Markov Decision Process (MDP) kommer ind i billedet.

Hvor vi besvarer vores grundlæggende spørgsmål, dvs. Hvordan vi formulerer RL-problemer matematisk (ved hjælp af MDP), er vi nødt til at udvikle vores intuition om :
- Agent-miljøforholdet
- Markov-egenskab
- Markov-proces og Markov-kæder
- Markov Reward Process (MRP)
- Bellman-ligning
- Markov Reward Process
Grib din kaffe og stop ikke, før du er stolt!🧐
Agent-miljøforholdet
Først skal vi se på nogle formelle definitioner :
Agent : Softwareprogrammer, der træffer intelligente beslutninger, og de er de lærende i RL. Disse agenter interagerer med miljøet ved hjælp af handlinger og modtager belønninger baseret på deres handlinger.
Miljø :Det er demonstrationen af det problem, der skal løses.Nu kan vi have et virkeligt miljø eller et simuleret miljø, som vores agent skal interagere med.

State : Dette er agenternes position på et bestemt tidstrin i miljøet.Så hver gang en agent udfører en handling, giver miljøet agenten en belønning og en ny tilstand, som agenten nåede frem til ved at udføre handlingen.
Alt, som agenten ikke kan ændre vilkårligt, anses for at være en del af miljøet. I enkle vendinger kan handlinger være enhver beslutning, som vi ønsker, at agenten skal lære, og tilstand kan være alt, som kan være nyttigt ved valg af handlinger. Vi antager ikke, at alt i miljøet er ukendt for agenten, f.eks. anses belønningsberegning for at være en del af miljøet, selv om agenten ved en smule om, hvordan belønningen beregnes som en funktion af dens handlinger og de tilstande, hvori de udføres. Dette skyldes, at belønninger ikke kan ændres vilkårligt af agenten. Nogle gange er agenten måske fuldt ud klar over sine omgivelser, men finder det stadig vanskeligt at maksimere belønningen, ligesom vi måske ved, hvordan man spiller Rubiks terning, men stadig ikke kan løse den. Så vi kan roligt sige, at agent-miljø-forholdet repræsenterer grænsen for agentens kontrol og ikke dens viden.
Markov-egenskaben
Transition : At bevæge sig fra en tilstand til en anden kaldes Transition.
Transition Sandsynlighed: Sandsynligheden for, at agenten vil bevæge sig fra en tilstand til en anden, kaldes overgangssandsynlighed.
Markov-egenskaben fastslår, at :
“Fremtiden er uafhængig af fortiden givet nutiden”
Matematisk kan vi udtrykke dette udsagn som :
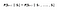
S betegner agentens nuværende tilstand, og s betegner den næste tilstand. Det, som denne ligning betyder, er, at overgangen fra tilstand S til S er helt uafhængig af fortiden. Så RHS i ligningen betyder det samme som LHS, hvis systemet har en Markov-egenskab. Intuitivt betyder det, at vores aktuelle tilstand allerede indfanger informationen om de tidligere tilstande.
Sandsynlighed for overgangstilstand :
Som vi nu kender til overgangssandsynlighed kan vi definere sandsynligheden for overgangstilstand som følger :
For Markov-tilstand fra S til S dvs. enhver anden efterfølgertilstand , er statsovergangssandsynligheden givet ved
Vi kan formulere statsovergangssandsynligheden til en statsovergangssandsynlighedsmatrix ved :

Hver række i matrixen repræsenterer sandsynligheden for at bevæge sig fra vores oprindelige tilstand eller starttilstand til en hvilken som helst efterfølgertilstand.Summen af hver række er lig med 1.
Markov-proces eller Markov-kæder
Markov-proces er den hukommelsesløse tilfældige proces, dvs. en sekvens af en tilfældig tilstand S,S,….S med en Markov-egenskab.Så det er grundlæggende en sekvens af tilstande med Markov-egenskaben.Den kan defineres ved hjælp af et sæt tilstande(S) og overgangssandsynlighedsmatrix (P).Dynamikken i miljøet kan fuldt ud defineres ved hjælp af tilstande(S) og overgangssandsynlighedsmatrix(P).
Men hvad betyder tilfældig proces ?
For at besvare dette spørgsmål skal vi se på et eksempel:
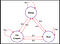
Kanterne i træet angiver overgangssandsynligheden. Lad os tage nogle prøver fra denne kæde. Lad os nu antage, at vi sov, og den ifølge sandsynlighedsfordelingen er der 0,6 chance for, at vi løber, og 0,2 chance for, at vi sover mere, og igen 0,2 chance for, at vi spiser is. På samme måde kan vi tænke på andre sekvenser, som vi kan udtage prøver fra denne kæde.
Nogle prøver fra kæden :
I de to ovenstående sekvenser er det, vi ser, at vi får tilfældige sæt af tilstande (S) (dvs. Søvn,Is,Søvn ) hver gang vi kører kæden.Håber, det er nu klart, hvorfor Markov-processen kaldes et tilfældigt sæt af sekvenser.
Hvor vi går til Markov Reward-processen, skal vi se på nogle vigtige begreber, som vil hjælpe os med at forstå MRP’er.
Belønning og returnering
Belønninger er de numeriske værdier, som agenten modtager ved at udføre en handling ved en eller flere tilstande i miljøet. Den numeriske værdi kan være positiv eller negativ baseret på agentens handlinger.
In Reinforcement learning, we care about maximizing the cumulative reward (all the rewards agent receives from the environment) instead of, the reward agent receives from the current state(also called immediate reward). Denne samlede sum af den belønning, som agenten modtager fra omgivelserne, kaldes afkast.
Vi kan definere Returns som :
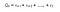
r er den belønning, som agenten modtager på tidstrin t, mens han udfører en handling(a) for at bevæge sig fra en tilstand til en anden. På samme måde er r den belønning, som agenten modtager på tidstrin t ved at udføre en handling for at flytte til en anden tilstand. Og r er den belønning, som agenten modtager på det sidste tidstrin ved at udføre en handling for at flytte til en anden tilstand.
Episodiske og kontinuerlige opgaver
Episodiske opgaver: Vi kan sige, at de har endelige tilstande. I f.eks. racerspil starter vi spillet (starter løbet) og spiller det, indtil spillet er slut (løbet slutter!). Dette kaldes en episode. Når vi genstarter spillet, starter det fra en begyndelsestilstand, og derfor er hver episode uafhængig.
Kontinuerlige opgaver : Det er de opgaver, der ikke har nogen ende, dvs. de har ingen terminaltilstand.Disse typer opgaver vil aldrig ende.For eksempel: At lære at kode!
Nu er det nemt at beregne afkastet af de episodiske opgaver, da de til sidst vil ende, men hvad med de kontinuerlige opgaver, da det vil fortsætte for evigt. Afkastet fra summerer op til uendeligt! Så hvordan definerer vi afkastet for kontinuerlige opgaver?
Det er her, vi har brug for rabatfaktor (ɤ).
Rabatfaktor (ɤ): Den bestemmer, hvor stor vægt der skal lægges på den umiddelbare belønning og fremtidige belønninger. Dette hjælper os grundlæggende til at undgå uendelighed som belønning i kontinuerlige opgaver. Den har en værdi mellem 0 og 1. En værdi på 0 betyder, at der lægges mere vægt på den umiddelbare belønning, og en værdi på 1 betyder, at der lægges mere vægt på fremtidige belønninger. I praksis vil en diskonteringsfaktor på 0 aldrig lære noget, da den kun tager hensyn til den umiddelbare belønning, og en diskonteringsfaktor på 1 vil gå videre til fremtidige belønninger, hvilket kan føre til uendelighed. Derfor ligger den optimale værdi for diskonteringsfaktoren på mellem 0,2 og 0,8.
Så vi kan definere afkast ved hjælp af diskonteringsfaktoren som følger :(Lad os sige, at dette er ligning 1 ,da vi senere skal bruge denne ligning til at udlede Bellman-ligningen)

Lad os forstå det med et eksempel,antag at du bor et sted, hvor du står over for vandmangel, så hvis nogen kommer til dig og siger, at han vil give dig 100 liter vand!(antag venligst!) i de næste 15 timer som en funktion af en parameter (ɤ).Lad os se på to muligheder: (Lad os sige, at dette er ligning 1, da vi skal bruge denne ligning senere til at udlede Bellman-ligningen)
En med diskonteringsfaktor (ɤ) 0.8 :
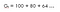
Det betyder, at vi skal vente til 15. time, fordi nedsættelsen ikke er særlig markant , så det er stadig værd at gå til sidst.Det betyder, at vi også er interesserede i fremtidige belønninger.Så hvis diskonteringsfaktoren er tæt på 1, vil vi gøre en indsats for at gå til slutningen, da belønningen er af væsentlig betydning.
For det andet, med diskonteringsfaktor (ɤ) 0,2 :
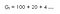
Det betyder, at vi er mere interesserede i tidlige belønninger, da belønningerne bliver betydeligt lavere i timen.Så vi ønsker måske ikke at vente til slutningen (til 15. time), da det vil være værdiløst.Så hvis diskonteringsfaktoren er tæt på nul, er øjeblikkelige belønninger vigtigere end fremtidige.
Så hvilken værdi af diskonteringsfaktoren skal vi bruge?
Det afhænger af den opgave, som vi ønsker at træne en agent til. Lad os antage, at målet i et skakspil er at besejre modstanderens konge. Hvis vi lægger vægt på de umiddelbare belønninger som f.eks. en belønning ved en bonde, der besejrer en modstanders spiller, så vil agenten lære at udføre disse delmål, uanset om hans spillere også bliver besejret. Så i denne opgave er fremtidige belønninger vigtigere. I nogle tilfælde foretrækker vi måske at bruge umiddelbare belønninger som f.eks. vandeksemplet, som vi så tidligere.
Markov Reward Process
Sindtil nu har vi set, hvordan Markov-kæden definerede dynamikken i et miljø ved hjælp af sæt af tilstande (S) og overgangssandsynlighedsmatrix (P).Men vi ved, at Reinforcement Learning handler om målet om at maksimere belønningen.Så lad os tilføje belønning til vores Markov-kæde.Dette giver os Markov Reward Process.
Markov Reward Process : Som navnet antyder, er MDP’er Markov-kæder med værdibedømmelse.Grundlæggende får vi en værdi fra hver tilstand, som vores agent befinder sig i.
Matematisk set definerer vi Markov Reward Process som :
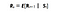
Hvad denne ligning betyder er, hvor meget belønning (Rs) vi får fra en bestemt tilstand S. Dette fortæller os den umiddelbare belønning fra den bestemte tilstand, vores agent er i. Som vi vil se i den næste historie, hvordan vi maksimerer disse belønninger fra hver tilstand, som vores agent befinder sig i. I enkle vendinger maksimerer vi den kumulative belønning, som vi får fra hver tilstand.
Vi definerer MRP som (S,P,R,ɤ) ,hvor :
- S er et sæt tilstande,
- P er overgangssandsynlighedsmatrixen,
- R er belønningsfunktionen , som vi så tidligere,
- ɤ er diskonteringsfaktoren
Markov Decision Process
Nu skal vi udvikle vores intuition for Bellman-ligningen og Markov Decision Process.
Politisk funktion og værdifunktion
Værdifunktion bestemmer, hvor godt det er for agenten at være i en bestemt tilstand. For at bestemme, hvor godt det vil være at være i en bestemt tilstand, skal det naturligvis afhænge af nogle handlinger, som den vil foretage. Det er her, at politikken kommer ind i billedet. En politik definerer, hvilke handlinger der skal udføres i en bestemt tilstand s.

En politik er en simpel funktion, der definerer en sandsynlighedsfordeling over Handlinger (a∈ A) for hver tilstand (s ∈ S). Hvis en agent på tidspunkt t følger en politik π, så er π(a|s) sandsynligheden for, at agenten med at foretage handling (a ) på et bestemt tidstrin (t). i Reinforcement Learning bestemmer agentens erfaring ændringen i politikken. Matematisk er en politik defineret som følger :
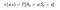
Nu, hvordan vi finder en værdi af en tilstand.Værdien af tilstand s, når agenten følger en politik π, som betegnes vπ(s), er det forventede afkast, der starter fra s og følger en politik π for de næste tilstande,indtil vi når terminaltilstanden.Vi kan formulere dette som :(Denne funktion kaldes også State-value Function)

Denne ligning giver os det forventede afkast, der starter fra tilstand(s) og går til de efterfølgende tilstande derefter, med politikken π. En ting at bemærke er, at det afkast, vi får, er stokastisk, mens værdien af en tilstand ikke er stokastisk. Det er forventningen til afkastet fra starttilstand s og derefter til enhver anden tilstand. Det skal også bemærkes, at værdien af den endelige tilstand (hvis der er nogen) er nul. Lad os se på et eksempel :
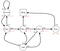
Sæt, at vores starttilstand er klasse 2, og vi bevæger os til klasse 3, derefter passerer vi og derefter sover. kort sagt, klasse 2 > klasse 3 > passerer > sover.
Vores forventede afkast er med diskonteringsfaktor 0,5:
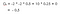
Note:Det er -2 + (-2 * 0.5) + 10 * 0,25 + 0 i stedet for -2 * -2 * -2 * 0,5 + 10 * 0,25 + 0. Så er værdien af klasse 2 -0,5 .
Bellman-ligning for værdifunktion
Bellman-ligning hjælper os med at finde optimale politikker og værdifunktioner.Vi ved, at vores politik ændrer sig med erfaringen, så vi vil have forskellige værdifunktioner i henhold til forskellige politikker.Optimal værdifunktion er en funktion, der giver maksimal værdi sammenlignet med alle andre værdifunktioner.
Bellman-ligningen fastslår, at værdifunktionen kan nedbrydes i to dele:
Matematisk set kan vi definere Bellman-ligningen som :
Lad os forstå, hvad denne ligning siger ved hjælp af et eksempel :
Sæt, der er en robot i en eller anden tilstand (s), og så bevæger han sig fra denne tilstand til en anden tilstand (s’). Nu er spørgsmålet, hvor godt det var for robotten at være i den tilstand (s). Ved hjælp af Bellman-ligningen kan vi sige, at det er forventningen om den belønning, den fik ved at forlade tilstanden (s) plus værdien af den tilstand (s’), som den flyttede til.
Lad os se på et andet eksempel :
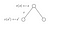
Vi ønsker at kende værdien af tilstand s.Værdien af tilstand(e) er den belønning, vi fik ved at forlade denne tilstand, plus den diskonterede værdi af den tilstand, vi landede på, ganget med overgangssandsynligheden for, at vi vil bevæge os ind i den.
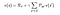
Overstående ligning kan udtrykkes i matrixform på følgende måde :

Hvor v er værdien af den tilstand vi var i, som er lig med den umiddelbare belønning plus den diskonterede værdi af den næste tilstand ganget med sandsynligheden for at bevæge sig ind i denne tilstand.
Den løbende tidskompleksitet for denne beregning er O(n³). Derfor er dette klart ikke en praktisk løsning til løsning af større MRP’er (det samme gælder også for MDP’er). i senere blogs vil vi se på mere effektive metoder som dynamisk programmering (værdi-iteration og politik-iteration), Monte-Claro-metoder og TD-Learning.
Vi kommer til at tale meget mere detaljeret om Bellman-ligningen i den næste historie.
Hvad er Markov Decision Process ?
Markov Decision Process : Det er Markov Reward Process med en beslutninger.Alt er det samme som MRP, men nu har vi et egentligt agentur, der træffer beslutninger eller foretager handlinger.
Det er en tupel af (S, A, P, R, 𝛾), hvor:
- S er et sæt tilstande,
- A er sættet af handlinger, som agenten kan vælge at foretage,
- P er overgangssandsynlighedsmatrixen,
- R er den belønning, der akkumuleres ved agentens handlinger,
- 𝛾 er diskonteringsfaktoren.
P og R vil have en lille ændring w.r.t handlinger som følger :
Transition Probability Matrix
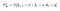
Belønningsfunktion
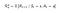
Nu er vores belønningsfunktion afhængig af handlingen.
Indtil nu har vi talt om at få en belønning (r), når vores agent går gennem et sæt tilstande (s) efter en politik π.I Markov Decision Process (MDP) er politikken faktisk mekanismen til at træffe beslutninger.Så nu har vi en mekanisme, som vælger at foretage en handling.
Politikker i en MDP afhænger af den aktuelle tilstand.De afhænger ikke af historien.Det er Markov-egenskaben.Så den aktuelle tilstand, vi befinder os i, karakteriserer historien.
Vi har allerede set, hvor godt det er for agenten at være i en bestemt tilstand (Tilstandsværdifunktion).Lad os nu se, hvor godt det er at foretage en bestemt handling efter en politik π fra tilstand s (Aktionsværdifunktion).
Status-aktionsværdifunktion eller Q-funktion
Denne funktion angiver, hvor godt det er for agenten at foretage en handling (a) i en tilstand (s) med en politik π.
Matematisk kan vi definere State-action value function som :

Basisk set fortæller den os værdien af at udføre en bestemt handling (a) i en tilstand (s) med en politik π.
Lad os se på et eksempel på Markov Decision Process :
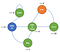
Nu kan vi se, at der ikke er flere sandsynligheder.Nu har vores agent faktisk valg at træffe, f.eks. kan vi efter at være vågnet vælge at se netflix eller kode og fejlfinding.Selvfølgelig er agentens handlinger defineret i forhold til en politik π og vil blive belønnet i overensstemmelse hermed.