I den generaliserede lineære modeller tutorial lærte vi om forskellige GLM’er som lineær regression, logistisk regression osv.. I denne tutorial i TechVidvan’s R tutorial-serie vil vi se nærmere på lineær regression i R i detaljer. Vi vil lære, hvad lineær regression i R er, og hvordan man implementerer den i R. Vi vil se på den mindste kvadrat estimationsmetode og vil også lære, hvordan man kontrollerer modellens nøjagtighed.

Så, uden videre, lad os komme i gang!

Linear regression i R

Linear regression i R er en metode, der bruges til at forudsige værdien af en variabel ved hjælp af værdien(e) af en eller flere inputprædiktorvariable. Målet med lineær regression er at etablere en lineær sammenhæng mellem den ønskede udgangsvariabel og inputprædiktorerne.

At modellere en kontinuerlig variabel Y som en funktion af en eller flere inputprædiktorvariable Xi, således at funktionen kan bruges til at forudsige værdien af Y, når kun værdierne af Xi er kendt. Den generelle form for en sådan lineær sammenhæng er:

Y=?0+?1 X

Her er ?0 interceptet
og ?1 er hældningen.

Typer af lineær regression i R

Der findes to typer af lineær regression i R:

• Enkle lineær regression
• Multipel lineær regression

Lad os se på disse én for én.

Enkle lineær regression i R

Enkle lineær regression har til formål at finde en lineær sammenhæng mellem to kontinuerlige variabler. Det er vigtigt at bemærke, at sammenhængen er af statistisk art og ikke deterministisk.

En deterministisk sammenhæng er en sammenhæng, hvor værdien af den ene variabel kan findes nøjagtigt ved hjælp af værdien af den anden variabel. Et eksempel på en deterministisk relation er den mellem kilometer og miles. Ved hjælp af kilometerværdien kan vi nøjagtigt finde afstanden i miles. En statistisk relation er ikke nøjagtig og har altid en forudsigelsesfejl. Hvis vi f.eks. får tilstrækkeligt med data, kan vi finde en sammenhæng mellem en persons højde og vægt, men der vil altid være en fejlmargin, og der vil være undtagelsestilfælde.

Den idé, der ligger bag simpel lineær regression, er at finde en linje, der passer bedst til de givne værdier af begge variabler. Denne linje kan så hjælpe os med at finde værdierne for den afhængige variabel, når de mangler.

Lad os undersøge dette ved hjælp af et eksempel. Vi har et datasæt bestående af højder og vægte for 500 personer. Vores mål her er at opbygge en lineær regressionsmodel, der formulerer sammenhængen mellem højde og vægt, således at når vi giver højde(Y) som input til modellen, kan den give vægt(X) tilbage til os med minimal fejlmargin eller fejlmargin.

Y=b0+b1X

Værdierne for b0 og b1 skal vælges således, at de minimerer fejlmargenen. Fejlmetrikken kan bruges til at måle modellens nøjagtighed.

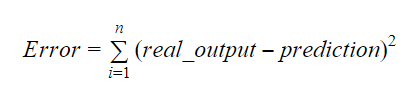
Vi kan beregne hældningen eller koefficienten som: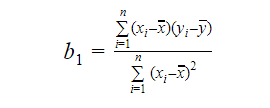

Værdien af b1 giver os indsigt i arten af forholdet mellem de afhængige og de uafhængige variabler.

• Hvis b1 > 0, så har variablerne en positiv sammenhæng dvs. en stigning i x vil resultere i en stigning i y.
• Hvis b1 < 0, så har variablerne en negativ sammenhæng, dvs. en stigning i x vil resultere i et fald i y.

Værdien af b0 eller interceptet kan beregnes på følgende måde: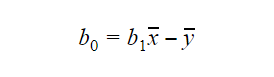
Værdien af b0 kan også give mange oplysninger om modellen og omvendt.

Hvis modellen ikke omfatter x=0, så er forudsigelsen meningsløs uden b1. For at modellen kun har b0 og ikke b1 i den på et hvilket som helst punkt, skal værdien af x være 0 på det pågældende punkt. I tilfælde som f.eks. højde kan x ikke være 0, og en persons højde kan ikke være 0. Derfor er en sådan model meningsløs med kun b0.

Hvis b0-terminen mangler, vil modellen passere gennem oprindelsen, hvilket vil betyde, at forudsigelsen og regressionskoefficienten (hældningen) vil være skævvredet.

Multipel lineær regression i R

Multipel lineær regression er en udvidelse af simpel lineær regression. I multipel lineær regression har vi til formål at skabe en lineær model, der kan forudsige værdien af målvariablen ved hjælp af værdierne af flere prædiktorvariabler. Den generelle form for en sådan funktion er som følger:

Y=b0+b1X1+b2X2+…+bnXn

Vurdering af modellens nøjagtighed

Der findes forskellige metoder til at vurdere modellens kvalitet og nøjagtighed. Lad os se på nogle af disse metoder én ad gangen.

R-kvadrat

Den virkelige information i data er den varians, der er formidlet i dem. R-kvadrat fortæller os, hvor stor en del af variationen i målvariablen (y), der forklares af modellen. Vi kan finde R-kvadratmålet for en model ved hjælp af følgende formel: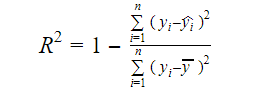

Hvor,

• yi er den tilpassede værdi af y for observation i
• y er middelværdien af Y.

En lavere værdi af R-kvadrat betyder en lavere nøjagtighed af modellen. R-kvadratmålet er dog ikke nødvendigvis en endelig afgørende faktor.

Akorrigeret R-kvadrat

Da antallet af variabler i modellen stiger, stiger R-kvadratværdien også. Dette medfører også fejl i den variation, der forklares af de nyligt tilføjede variabler. Derfor justerer vi formlen for R-kvadrat for flere variabler.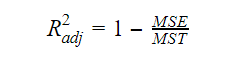
Her står MSE for Mean Standard Error, som er:

Og MST står for Mean Standard Total, som er givet ved: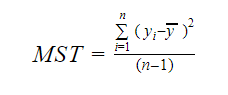

Hvor n er antallet af observationer og q er antallet af koefficienter.

Sammenhængen mellem R-kvadrat og justeret R-kvadrat er: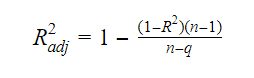

Standardfejl og F-statistik

Standardfejlen og F-statistikken er begge mål for kvaliteten af tilpasningen af en model. Formlerne for standardfejl og F-statistik er:

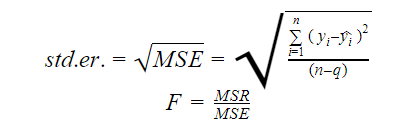
Hvor MSR står for Mean Square Regression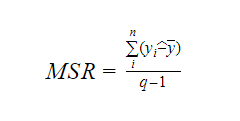

AIC og BIC

Akaikes informationskriterium og Bayesian Information Criterion er mål for kvaliteten af tilpasningen af statistiske modeller. De kan også anvendes som kriterier for valg af en model.

AIC=(-2)*ln(L)+2*k
BIC=(-2)*ln(L)+k*ln(n)

Hvor,

• L er sandsynlighedsfunktionen,
• k er antallet af modelparametre,
• n er stikprøvestørrelsen.

lm-funktionen i R

Den lm()-funktion i R passer til lineære modeller. Den kan udføre regression og analyse af varians og kovarians. Syntaksen for lm-funktionen er som følger:

lm(formula, data, subset, weights, na.action,method = "qr", model = TRUE, x = FALSE, y = FALSE, qr = TRUE,singular.ok = TRUE, offset, …)

Hvor,

• formula er et objekt af klassen “formula” og er en symbolsk repræsentation af den model, der skal tilpasses,
• data er den dataramme eller liste, der indeholder variablerne i formlen(data er et valgfrit argument. Hvis det mangler, henter funktionen variablerne fra miljøet),
• subset er en valgfri vektor, der indeholder en delmængde af de observationer, der skal bruges i tilpasningen,
• weights er en valgfri vektor, der angiver de vægte, der skal bruges i tilpasningen,
• na.action er en funktion, der viser, hvad der skal ske, når der forekommer NA’er i dataene,
• method angiver metoden til tilpasning af modellen,
• model, x, y og qr er logicals, der styrer, om de tilsvarende værdier skal returneres med outputtet eller ej. Disse værdier er:
• model: modelrammen
• x: modelmatrixen
• y: responset
• qr: qr-dekompositionen
• singular.ok er en logik, der styrer, om singulære tilpasninger er tilladt eller ej,
• offset er en på forhånd kendt prædiktor, der skal bruges i modellen,
• . . er yderligere argumenter, der skal overføres til regressionsfunktionerne på lavere niveau.

Praktisk eksempel på lineær regression i R

Det er nok teori for nu. Lad os tage et kig på, hvordan man implementerer alt dette. Vi skal tilpasse en lineær model ved hjælp af lineær regression i R ved hjælp af funktionen lm(). Vi vil også kontrollere modellens tilpasningskvalitet bagefter. Lad os bruge datasættet cars, som leveres som standard i grundpakken R.

1. Lad os starte med en grafisk analyse af datasættet for at blive mere fortrolige med det. For at gøre det vil vi tegne et spredningsdiagram og kontrollere, hvad det fortæller os om dataene.

Vi kan bruge funktionen scatter.smooth() til at oprette et spredningsdiagram for datasættet.

scatter.smooth(x=cars$speed,y=cars$dist,main="TechVidvan Dist ~ Speed")

Output

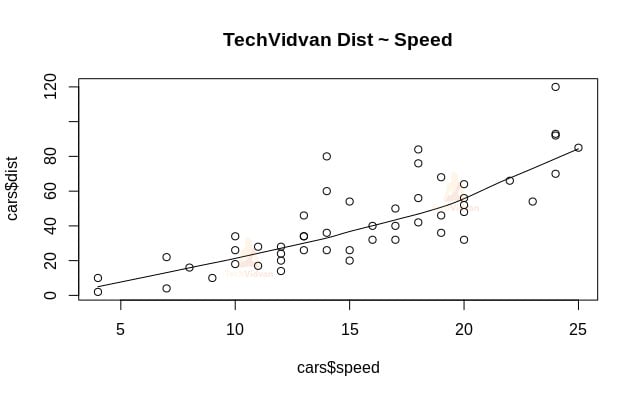
Spredningsdiagrammet viser os en positiv korrelation mellem afstand og hastighed. Det tyder på en lineært stigende sammenhæng mellem de to variabler. Dette gør dataene egnede til lineær regression, da en lineær sammenhæng er en grundlæggende antagelse for tilpasning af en lineær model på data.

2. Nu hvor vi har verificeret, at lineær regression er egnet til dataene, kan vi bruge funktionen lm() til at tilpasse en lineær model til dem.

Linear_model <- lm(dist~speed,data=cars)print(Linear_model)

Output

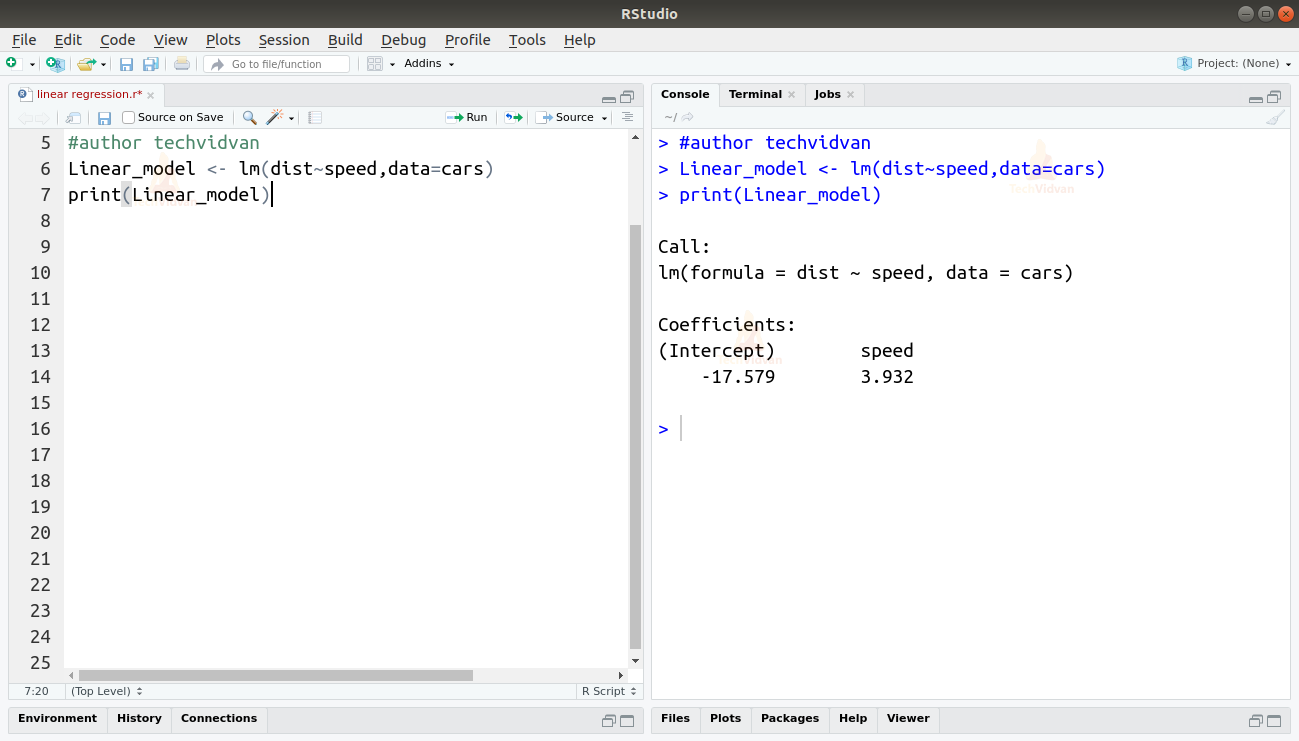
Outputtet fra funktionen lm() viser os interceptet og hastighedskoefficienten. Dermed defineres den lineære sammenhæng mellem afstand og hastighed som:

Distance=Intercept+koefficient*hastighed

Distance=-17,579+3,932*hastighed

3. Nu da vi har tilpasset en model, skal vi kontrollere kvaliteten eller godheden af tilpasningen. Lad os starte med at kontrollere resuméet af den lineære model ved hjælp af funktionen summary().

summary(Linear_model)

Output

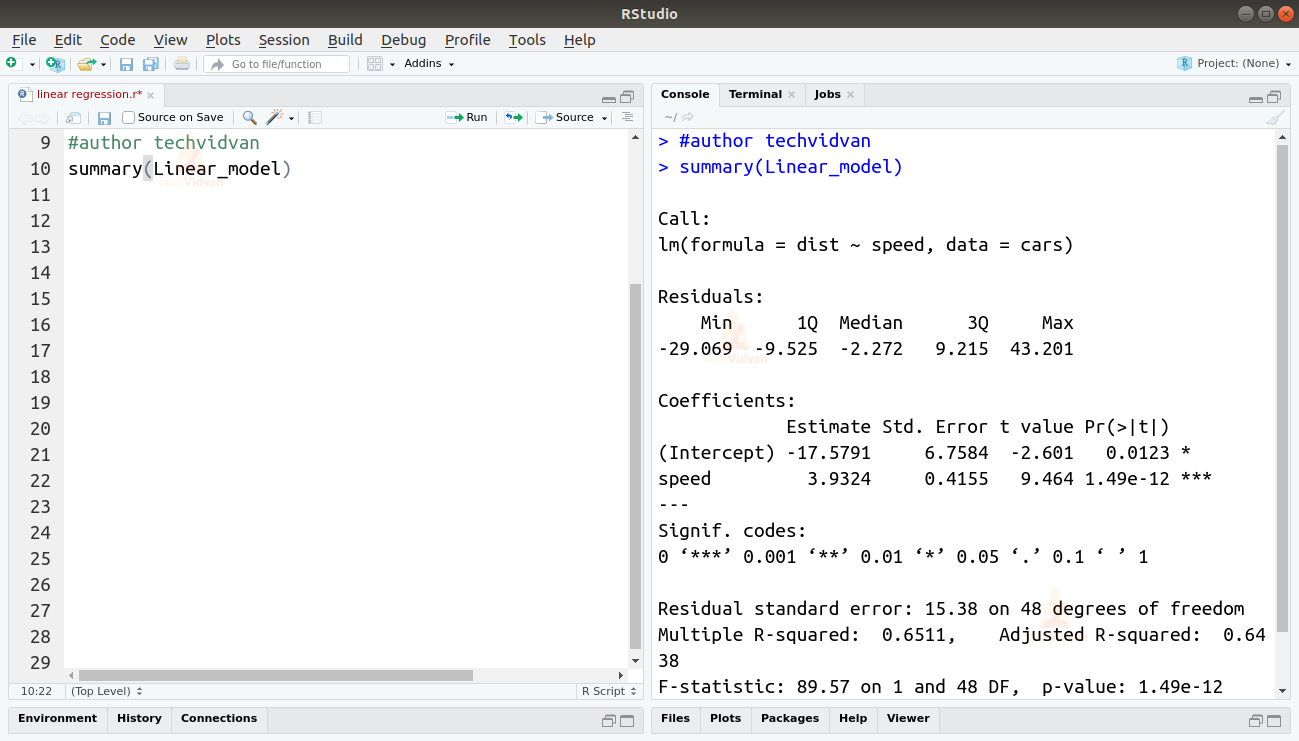
Funktionen summary() giver os et par vigtige mål, der kan hjælpe os med at diagnosticere modellens tilpasning. p-værdien er et vigtigt mål for, hvor godt en model passer til modellen. En model siges ikke at være egnet, hvis p-værdien er mere end et forudbestemt statistisk signifikansniveau, som ideelt set er 0,05.

Sammenfatningen giver os også t-værdien. Jo større t-værdien er, jo bedre passer modellen.
Vi kan også finde AIC- og BIC-værdien ved at bruge funktionerne AIC() og BIC().

AIC(Linear_model)BIC(Linear_model)

Output

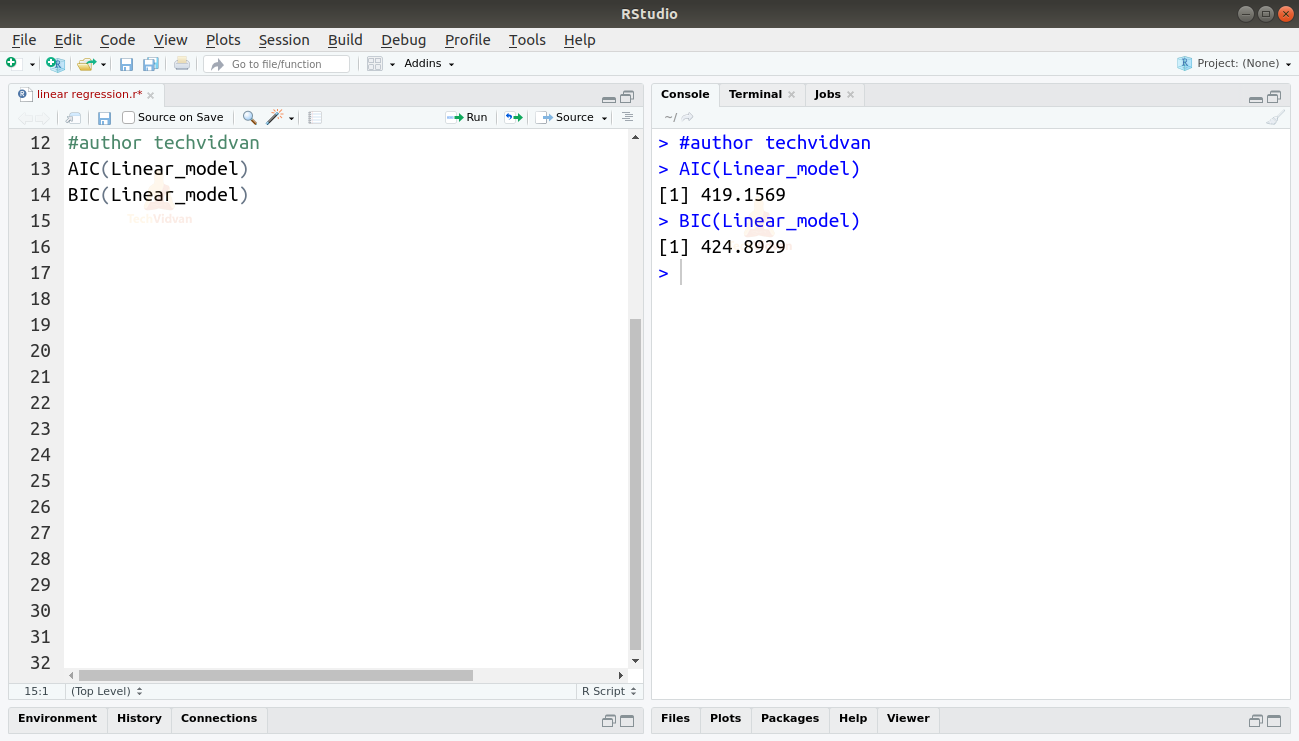
Den model, der resulterer i de laveste AIC- og BIC-scorer, er den mest foretrukne.

Summary

I dette kapitel i TechVidvans R tutorial-serie om lineær regression lærte vi om lineær regression. Vi lærte om simpel lineær regression og multipel lineær regression. Derefter studerede vi forskellige mål til at vurdere modellens kvalitet eller nøjagtighed, såsom R2, justeret R2, standardfejl, F-statistik, AIC og BIC. Derefter lærte vi, hvordan man implementerer lineær regression i R. Derefter kontrollerede vi kvaliteten af modellens tilpasning i R.

Del din bedømmelse på Google, hvis du kunne lide tutorial om lineær regression.